Griffiths D. Head First Statistics
Подождите немного. Документ загружается.


you are here 4 471
estimating populations and samples
This is a slightly different problem from last time. We’re told what the
population mean and variance are for the packets of gumballs, and
we have a sample of packets we need to figure out probabilities for.
Instead of working out probabilities for the sample proportion, this
time we need to work out probabilities for the sample mean.
Before we can work out probabilities for the sample mean, we need to
figure out its probability distribution. Here’s what we need to do:
Look at all possible samples the same size as the one we’re
considering.
If we have a sample of size n, we need to consider all possible samples of
size n. There are 30 packets of gumballs, so in this case, n is 30.
11
Look at the distribution formed by all the samples, and
find the expectation and variance for the sample mean.
Every sample is different, and the number of gumballs in each packet
varies.
22
Once we know how the sample mean is distributed, use it to
find probabilities.
If we know how the means of all possible samples are distributed, we can
use it to find probabilities for the mean in a random sample, in this case
the, packets of gumballs.
33
Let’s take a look at how to tackle this.
The population in this case is
all the packets of gumballs.
The sample comprises 30
such packets.
We need probabilities for the sample mean
472 Chapter 11
Sample of X
X
E(X) = μ
Var(X) = σ
2
The sampling distribution of the mean
So how do we find the distribution of the sample means?
Let’s start with the population of gumball packets. We’ve been told what
the mean and variance is for the population, and we’ll represent these with
μ and σ
2
. We can represent the number of gumballs in a packet with X.
Each packet chosen at random is an independent observation of X,
so each gumball packet follows the same distribution. In other words, if
X
i
represents the number of gumballs in a packet chosen at random, then
each X
i
has an expectation of μ and variance σ
2
.
Now let’s take a sample of n gumball packets. We can label the number of
gumballs in packet X
1
through X
n
. Each X
i
is an independent observation
of X, which means that they follow the same distribution. Each X
i
has an
expectation of μ and variance σ
2
.
We can represent the mean of gumballs in these n packets of gumballs with
X. The value of X depends on how many gumballs are in each packet of
the n pockets, and to calculate it, you add up the total number of gumballs
and divide by n.
X = X
1
+ X
2
+ ... + X
n
n
The number of gumballs
in each packet follows
the same distribution.
X represents the
number of gumballs
in a packet.
X
i
E(X
i
) = μ
Var(X
i
) = σ
2
X
n
E(X
n
) = μ
Var(X
n
) = σ
2
Each X
i
is an independent
observation of X, so each
packet has the same
expectation and variance
for the number of gumballs.
This is the mean of the sample,
the mean number of gumballs in
the packets.
X
1
E(X
1
) = μ
Var(X
1
) = σ
2
distribution of sample means in depth

you are here 4 473
estimating populations and samples
There are many possible samples we could have taken of size n. Each
possible sample comprises n packets, which means that each sample
comprises n independent observations of X. The number of gumballs
in each randomly chosen packet follows the same distribution as all the
others, and we calculate the mean number of gumballs for each sample in
the same way.
Each sample contains
n packets, just like
the previous one.
Samples of X
Sample mean X
Sample mean X
Sample mean X
We can form a distribution out of all the sample means from all possible
samples. This is called the sampling distribution of means, or the
distribution of X.
So does this really help
us? What does it give us?
This is the mean number
of gumballs per packet in
this sample
The sampling distribution of means gives us a way of
calculating probabilities for the mean of a sample.
Before you can work out the probability of any variable, you need to
know about its probability distribution, and this means that if you want
to calculate probabilities for the sample mean, you need to know how the
sample means are distributed. In our particular case, we want to know
what the probability is of there being a mean of 8.5 gumballs or fewer in a
sample of 30 packets of gumballs.
Just as with the sampling distribution of proportions, before we can start
calculating probabilities, we need to know what the expectation and
variance are of the distribution.

474 Chapter 11
Find the expectation for X
So far, we’ve looked at how to construct the sampling distribution of
means. In other words, we consider all possible samples of size n and
form a distribution out of their means.
Before we can use it to find probabilities, we need to find the
expectation and variance of X. Let’s start by finding E(X).
Now X is the mean number of gumballs in each packet of gumballs in
our sample. In other words,
X = X
1
+ X
2
+ ... + X
n
n
where each X
i
represents the number of gumballs in the i’th packet of
gumballs. We can use this to help us find E(X).
E(X) = E
(
X
1
+ X
2
+ ... + X
n
)
n
= E
(
1
X
1
+
1
X
2
+ ... +
1
X
n
)
n n n
= E
(
1
X
1
)
+ E
(
1
X
2
)
+ ... + E
(
1
X
n
)
n n n
=
1
( E( X
1
) + E(X
2
) + ... + E(X
n
) )
n
These two expressions are
the same, just written in a
different way.
We can split this into n separate
expectations because
E(X + Y) = E(X) + E(Y).
Every expectation includes 1/n,
so we can take it out of the
expression. This comes from
E(aX) = aE(X).
This means that if we know what the expectation is for each X
i
, we’ll have
an expression for E(X).
Now each X
i
is an independent observation of X, and we already know
that E(X) = μ. This means that we can substitute μ for each E(X
i
) in the
above expression.
So where does this get us?
expectation of x
you are here 4 475
estimating populations and samples
The expectation of X is μ.
E(X
i
) = μ for every i.
This means that E(X) = μ. In other words, the average of all the possible
sample means of size n is the mean of the population they’re taken from.
You’re, in effect, finding the mean of all possible means.
This is actually quite intuitive. It means that overall, you’d expect the average
number of gumballs per packet in a sample to be the same as the average
number of gumballs per packet in the population. In our situation, the mean
number of gumballs in each packet in the population is 10, so this is what
we’d expect for the sample too.
There are n of these
Let’s replace each E(X
i
) with μ.
E(X) =
1
( μ + μ + ... + μ )
n
=
1
(nμ)
n
= μ
What else do we need to know in order to find probabilities for the sample
mean? How do you think we can find this?
If the population mean is 10 gumballs
per packet, you can expect the sample
mean to be 10 gumballs per packet too.

476 Chapter 11
What about the the variance of X?
So far we know what E(X) is, but before we can figure out any
probabilities for the sample mean, we need to know what Var(X) is.
This will bring us one step closer to finding out what the distribution
of X is like.
Why do we need to find
Var(X)? Isn’t it the same
as Var(X)? Isn’t it just σ
2
?
The distribution of X is different from the
distribution of X.
X represents the number of gumballs in a packet. We’ve been
told what the mean number of gumballs in a packet is, and
we’ve also been given the variance.
The mean number of
gumballs per packet is 10,
and the variance is 1.
X represents the mean number of gumballs in a sample, so the
distribution of X represents how the means of all possible samples are
distributed. E(X) refers to the mean value of the sample means, and
Var(X) refers to how they vary.
Finding Var(X) is actually a very similar process to finding E(X).
variance of x

you are here 4 477
estimating populations and samples
= Var
(
)
Statistics Magnets
Here are some equations for finding an expression for the variance of the sample mean.
Unfortunately, some parts of the equations have fallen off. Your task is to fill in the blanks
below by putting the magnets back in the right positions and derive the variance of the
sample mean.
σ
2
+ σ
2
+ ... + σ
2
1
X
1
+
1
X
2
+ ... +
1
X
n
n n n
1
X
1
n
1
X
2
n
1
X
n
n
= Var
(
)
+ Var
(
)
+ ... + Var
(
)
=
( Var( X
1
) + Var(X
2
) + ... + Var(X
n
) )
=
1
(
)
n
2
= n x 1 σ
2
n
2
=
σ
2
n
Var(X) = Var
(
X
1
+ X
2
+ ... + X
n
)
n
Hint: Look back at how we
found E(X). It might help
you.
1
n
2
(
)
478 Chapter 11
1
X
1
+
1
X
2
+ ... +
1
X
n
n n n
= Var
(
)
= Var
(
)
+ Var
(
)
+ ... + Var
(
)
=
( Var( X
1
) + Var(X
2
) + ... + Var(X
n
) )
=
1
(
)
n
2
=
Var(X) = Var
(
X
1
+ X
2
+ ... + X
n
)
n
Statistics Magnets Solution
Here are some equations for finding the variance of the sample mean. Unfortunately, some
parts of the equations have fallen off. Your task is to put the magnets back in the right
positions and derive the variance of the sample mean.
Well done if you got this far. The
derivation was a bit tricky, but
we’ve found out what the variance
of X is. We know how much the
sample mean might vary.
σ
2
+ σ
2
+ ... + σ
2
1
X
2
n
1
X
n
n
σ
2
n
statistics magnets solution
Don’t worry if you
didn’t complete
this exercise; it’s
hard.
Most exam boards won’t ask
you to derive this, and in real
life, you’ll just need to remember the result.
We’re just showing you where it comes from.
1
X
1
n
= n x 1 σ
2
n
2
1
n
2
(
)
you are here 4 479
estimating populations and samples
X Distribution
gumballs per packet
frequency
Sampling Distribution of the Means Up Close
Let’s take a closer look at the sampling distribution of means.
We started off by looking at the distribution of a population X. The mean of X
is given by μ, and the variance by σ
2
, so E(X) = μ and Var(X) = σ
2
.
We then took all possible samples of size n taken from the population X and
formed a distribution out of all the sample means, the distribution of X. The
mean and variance of this distribution are given by:
The standard deviation of X is the square root of the variance. The standard
deviation tells you how far away from μ the sample mean is likely to be, so it’s
known as the standard error of the mean.
E(X) = μ
Var(X) = σ
2
n
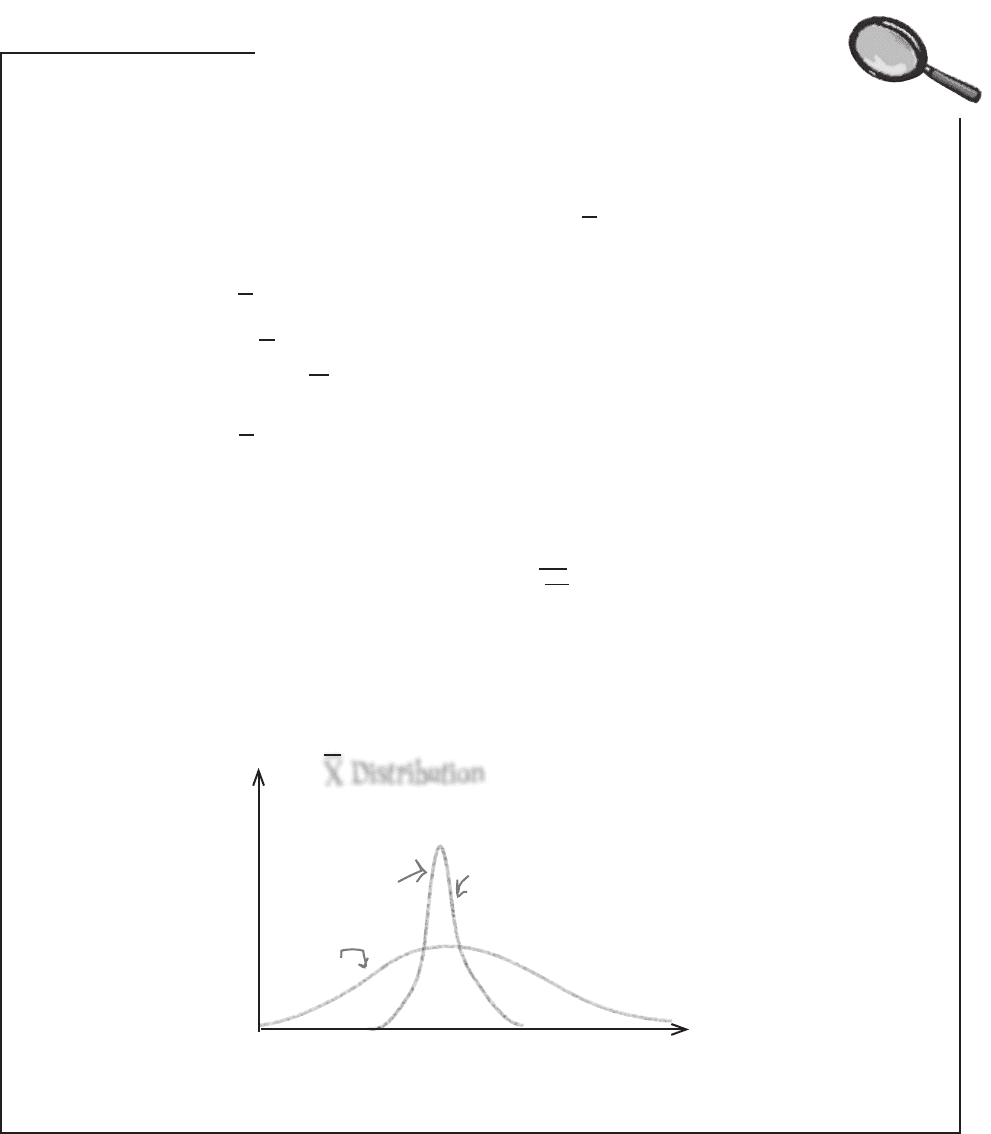
The standard error of the mean gets smaller as n gets larger. This means that
the more items there are in your sample, the more reliable your sample mean
becomes as an estimator for the population mean.
Large n
Small n
The larger n gets, the
smaller the standard
error becomes.
Standard error of the mean = σ
√n

480 Chapter 11
So how is X distributed?
So far we’ve found what the expectation and variance is for X. Before
we can find probabilities, though, we need to know exactly how X is
distributed.
Let’s start by looking at the distribution of X if X is normal.
Here’s a sketch of the distribution for X for different values of μ, σ
2
, and n,
where X is normally distributed. What do you notice?
For each of these combinations, the distribution of X is normal. In other
words
If X ~ N(μ, σ
2
), then X ~ N(μ, σ
2
/n)
These are the mean and
variance of X that we found
earlier.
But is the number of
gumballs in a packet
distributed normally?
What if it’s not?
X might not follow a normal distribution.
We need to know how X is distributed so that we can
work out probabilities for the sample mean. The trouble
is, we don’t know how X is distributed.
We need to know what distribution X follows if X isn’t
normal.
0.2
0.4
0.6
0.8
1.0
-3 -2 -1 0 1 2
3
µ = 0; σ
2
= 0.2
µ = 0, σ
2
= 5.0
µ = -2, σ
2
= 0.5
distribution of x
