Griffiths D. Head First Statistics

Подождите немного. Документ загружается.

you are here 4 481

estimating populations and samples

As n gets larger, X gets closer and closer to a normal distribution. We’ve

already seen that X is normal if X is normal. If X isn’t normal, then we can

still use the normal distribution to approximate the distribution of X if n is

sufficiently large.

In our current situation, we know what the mean and variance are for the

population, but we don’t know what its distribution is. However, since our

sample size is 30, this doesn’t matter. We can still use the normal distribution

to find probabilities for X.

This is called the central limit theorem.

Introducing the Central Limit Theorem

The central limit theorem says that if you take a sample from a non-normal

population X, and if the size of the sample is large, then the distribution of

X is approximately normal. If the mean and variance of the population are

μ and σ

, and n is , say, over 30, then

X ~ N(μ, σ

/n)

Does this look familiar? It’s the same distribution that we had when X

followed a normal distribution. The only difference is that if X is normal,

it doesn’t matter what size sample you use.

This is the mean

and variance of X.

If n is large, X can still be approximated by the normal distribution

By the central limit theorem, if your sample of X is

large, then X’s distribution is approximately normal.

482 Chapter 11

Using the central limit theorem

So how does the central limit theorem work in practice? Let’s take a look.

The binomial distribution

Imagine you have a population represented by X ~ B(n, p) where n is greater

than 30. As we’ve seen before, μ = np, and σ

= npq.

The central limit theorem tells us that in this situation, X ~ N(μ, σ

/n). To find

the distribution of X, we substitute in the values for the population. This means

that if we substitute in values for μ = np and σ

= npq, we get

X ~ N(np, pq)

For the binomial distribution, the mean of the population is

np, and the variance is npq. If we substitute this into the

sampling distribution, we get X ~ N(np, pq).

The Poisson distribution

Now suppose you have a population that follows a Poisson distribution of

X ~ Po(λ), again where n is greater than 30. For the Poisson distribution,

μ = σ

= λ.

As before, we can use the normal distribution to help us find probabilities for X.

If we substitute population parameters into X ~ N(μ, σ

/n), we get:

X ~ N(λ, λ/n)

Finding probabilities

Since X follows a normal distribution, this means that you can use standard

normal probability tables to look up probabilities. In other words, you can

find probabilities in exactly the same way you would for any other normal

distribution.

In general, you take the distribution X ~ N(μ, σ

/n) and substitute in values for

μ and σ

For the Poisson distribution, the mean and variance

are both λ. If we substitute this into the sampling

distribution, we get X ~ N(λ, λ/n).

central limit theorem

you are here 4 483

estimating populations and samples

Let’s apply this to Mighty Gumball’s problem.

The mean number of gumballs per packet is 10, and the variance is 1. If you take a sample of 30

packets, what’s the probability that the sample mean is 8.5 gumballs per packet or fewer? We’ll

guide you through the steps.

1. What’s the distribution of X?

2. What’s the value of P(X < 8.5)?

484 Chapter 11

Let’s apply this to Mighty Gumball’s problem.

The mean number of gumballs per packet is 10, and the variance is 1. If you take a sample of 30

packets, what’s the probability that the sample mean is 8.5 gumballs per packet or fewer? We’ll

guide you through the steps.

1. What’s the distribution of X?

We know that X ~ N(μ, σ

/n), μ = 10, σ

= 1, and n = 30, and 1/30 = 0.0333. So this gives us

X ~ N(10, 0.0333)

2. What’s the value of P(X < 8.5)?

As X ~ N(10, 0.0333), we need to find the standard score of 8.5 so that we can look up the result in

probability tables. This gives us

z = 8.5 - 10

0.0333

= -8.22 (to 2 decimal places)

P(Z < z) = P(Z < -8.22)

This probability is so small that it doesn’t appear on the probability tables. We can assume that an event with a

probability this small will hardly ever happen.

exercise solution

you are here 4 485

estimating populations and samples

Do I need to use any continuity

corrections with the central limit

theorem?

A: Good question, but no you don’t.

You use the central limit theorem to find

probabilities associated with the sample

mean rather than the values in the sample,

which means you don’t need to make any

sort of continuity correction.

Is there a relationship between

point estimators and sampling

distributions?

A: Yes, there is.

Let’s start with the mean. The point estimator

for the population mean is x, which means

that μ = x. Now, if we look at the expectation

for the sampling distribution of means, we

get E(X) = μ. The expectation of all the

sample means is given by μ, and we can

estimate μ with the sample mean.

Similarly, the point estimator for the

population proportion is p

, the sample

proportion, which means that p = p

. If

we take the expectation of all the sample

proportions, we get E(P

) = p. The

expectation of all the sample proportions is

given by p, and we can estimate p with the

sample proportion.

We’re not going to prove it, but we get a

similar result for the variance. We have

= s

, and E(S

) = σ

So is that a coincidence?

A: No, it’s not. The estimators are chosen

so that the expectation of a large number

of samples, all of size n and taken in the

same way, is equal to the true value of

the population parameter. We call these

estimators unbiased if this holds true.

An unbiased estimator is likely to be

accurate because on average across all

possible samples, it’s expected to be the

value of the true population parameter.

How does standard error come into

this?

A: The best unbiased estimator for a

population parameter is generally one with

the smallest variance. In other words, it’s the

one with the smallest standard error.

The sampling distribution of means is what

you get if you consider all possible samples of

size n taken from the same population and form

a distribution out of their means. We use X to

represent the sample mean random variable.

The expectation and variance of X are defined as

E(X) = μ

Var(X) = σ

where μ and σ

are the mean and variance of the

population.



The standard error of the mean is the standard

deviation of this distribution. It’s given by

Var(X)

If X ~ N(μ, σ

), then X ~ N(μ, σ

/n).

The central limit theorem says that if n is large

and X doesn’t follow a normal distribution, then

X ~ N(μ, σ

/n)



486 Chapter 11

Sampling saves the day!

The work you’ve done is awesome! My top customer

found an average of 8.5 gumballs in a sample of 30

packets, and you’ve told me the probability of getting

that result is extremely unlikely. That means I

don’t have to worry about compensating disgruntled

customers, which means more money for me!

You’ve made a lot of progress

Not only have you been able to come up with point

estimators for population parameters based on a single

sample, you’ve also been able to use population to calculate

probabilities in the sample. That’s pretty powerful.

hooray for gumball sampling

this is a new chapter 487

constructing confidence intervals

Guessing with Confidence

Sometimes samples don’t give quite the right result.

You’ve seen how you can use point estimators to estimate the precise value of the

population mean, variance, or proportion, but the trouble is, how can you be certain that

your estimate is completely accurate? After all, your assumptions about the population

rely on just one sample, and what if your sample’s off? In this chapter, you’ll see another

way of estimating population statistics, one that allows for uncertainty. Pick up your

probability tables, and we’ll show you the ins and outs of confidence intervals.

I put this in the

oven for 2.5 hours, but

if you bake yours for

1—5 hours, you should

be fine.

488 Chapter 12

Mighty Gumball is in trouble

We’re in trouble. Someone

else has conducted

independent tests and come

up with a different result.

They’re threatening to sue,

and that will cost me money.

Mighty Gumball used a sample of 100 gumballs to come up with a

point estimator of 62.7 minutes for the mean flavor duration, and

25 minutes for the population variance. The CEO announced on

primetime television that gumball flavor lasts for an average of 62.7

minutes. It’s the best estimate for flavor duration that could possibly

have been made based on the evidence, but what if it gave a slightly

wrong result?

If Mighty Gumball is sued because of the accuracy of their claims,

they could lose a lot of money and a lot of business. They need your

help to get them out of this.

The Mighty Gumball CEO has gone ahead with a range of

television advertisements, and he’s proudly announced exactly

how long the flavor of the super-long-lasting gumballs lasts for,

right down to the last second.

Unfortunately...

What do you think could have gone wrong? Should Mighty Gumball

have used the precise value of the point estimator in their advertising?

Why? Why not?

They need you to save them

another flavor favor

you are here 4 489

constructing confidence intervals

The problem with precision

As you saw in the last chapter, point estimators are the best estimate

we can possibly give for population statistics. You take a representative

sample of data and use this to estimate key statistics of the population

such as the mean, variance, and proportion. This means that the point

estimator for the mean flavor duration of super-long-lasting gumballs

was the best possible estimate we could possibly give.

The problem with deriving point estimators is that we rely on the

results of a single sample to give us a very precise estimate. We’ve

looked at ways of making the sample as representative as possible by

making sure the sample is unbiased, but we don’t know with absolute

certainty that it’s 100% representative, purely because we’re dealing

with a sample.

Now hold it right there!

Are you saying that point

estimators are no good?

After all that hard work?

Point estimators are valuable, but they may give

slight errors.

Because we’re not dealing with the entire population, all we’re doing

is giving a best estimate. If the sample we use is unbiased, then the

estimate is likely to be close to the true value of the population. The

question is, how close is close enough?

Rather than give a precise value as an estimate for the population

mean, there’s another approach we can take instead. We can specify

some interval as an estimation of flavor duration rather than a very

precise length of time. As an example, we could say that we expect

gumball flavor to last for between 55 and 65 minutes. This still gives

the impression that flavor lasts for approximately one hour, but it

allows for some margin of error.

The question is, how do we come up with the interval? It all depends

how confident you want to be in the results...

490 Chapter 12

Introducing confidence intervals

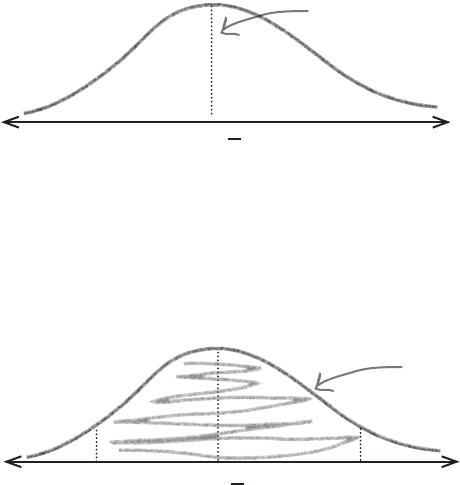
Up until now, we’ve estimated the mean amount of time that gumball flavor

lasts for by using a point estimator, based upon a sample of data. Using the

point estimator, we’ve been able to give a very precise estimate for the mean

duration of the flavor. Here’s a sketch showing the distribution of flavor

duration in the sample of gumballs.

With point estimators, we

estimate the population mean

using the mean of the samples.

So what happens if we specify an interval for the population mean instead?

Rather than specify an exact value, we can specify two values we expect

flavor duration to lie between. We place our point estimator for the mean

in the center of the interval and set the interval limits to this value plus or

minus some margin of error.

Rather than give a precise estimate for

the population mean, we can say that the

population mean is between values a and b.

The interval limits are chosen so that there’s a specified probability of the

population mean being between a and b. As an example, you may want to

choose a and b so that there’s a 95% chance of the interval containing the

population mean. In other words, you choose a and b so that

P(a < μ < b) = 0.95

We represent this interval as (a, b). As the exact value of a and b depends

on the degree of confidence you want to have that the interval contains the

population mean, (a, b) is called a confidence interval.

So how do we find the confidence interval for the population mean?

μ = x

all about confidence intervals