Griffiths D. Head First Statistics

Подождите немного. Документ загружается.

you are here 4 501

constructing confidence intervals

Finally, find the value of X

Now that we’ve rewritten the inequality, we’re very close to finding a

confidence interval for μ that describes the amount of time gumball

flavor typically lasts for. In other words, we use

P(X - 0.98 < μ < X + 0.98) = 0.95

Here’s a quick sketch.

Our confidence limits are given by X – 0.98 and X + 0.98. If we knew

what to use as a value for X, we’d have values for the confidence limits.

I wonder if we can use the

Mighty Gumball sample in

some way. Maybe we can use

the mean of the sample.

X is the distribution of sample means, so we can

use the value of x from the Mighty Gumball sample.

The confidence limits are given by X – 0.98 and X + 0.98. For the

Mighty Gumball sample, x is given by 62.7. Use this to come up

with values for the confidence limits.

- 0.98

+ 0.98

0.025

0.95

X X

502 Chapter 12

You’ve found the confidence interval

Congratulations! You’ve found your first confidence interval. You

found that there’s a 95% chance that the interval

(61.72, 63.68) contains the population mean for flavor duration.

That’s fantastic news! That

means I can update the fine

print on our advertisements.

That should handle any lawsuits.

Using confidence intervals in the television advertisement rather

than point estimators means that the CEO can give an accurate and

precise estimate for how long flavor lasts, but without having to give

a precise figure. It makes allowances for any margin of error there

might be in the sample.

The confidence limits are given by X - 0.98 and X + 0.98. For the

Mighty Gumball sample, x is given by 62.7. Use this to come up

with values for the confidence limits.

The confidence limits are given by X - 0.98 and X + 0.98. If we substitute in the mean of the sample, we get

confidence limits of 62.7 - 0.98 and 62.7 + 0.98. In other words, our confidence interval is (61.72, 63.68).

sharpen solution

you are here 4 503

constructing confidence intervals

So does that mean I have to

go through the same process

every single time I want to

construct a confidence interval?

We can take some shortcuts.

Constructing confidence intervals can be a repetitive process, so there

are some shortcuts you can take. It all comes down to the level of

confidence you want and the distribution of the test statistic.

Let’s take a look at some of the shortcuts we can take.

Let’s summarize the steps

Let’s look back at the steps we went through in order to construct the

confidence interval.

The first thing we did was choose the population statistic that

we needed to construct a confidence interval for. We needed to find a

confidence interval for the mean duration of gumball flavor, and this

meant that we needed to construct a confidence interval for μ.

Once we’d figured out which population we needed to construct a

confidence interval for, we had to find its sampling distribution.

We found the expectation and variance of the sampling distribution of

means, substituting in values for every statistic except for μ. We then

figured out that we could use a normal distribution for X.

After that, we decided on the level of confidence we needed for the

confidence interval. We decided to use a confidence level of 95%.

Finally, we had to find the confidence limits for the confidence

interval. We used the level of confidence and sampling distribution to

come up with a suitable confidence interval.

504 Chapter 12

Handy shortcuts for confidence intervals

Here are some of the shortcuts you can take when you calculate confidence

intervals. All you need to do is look at the population statistic you want to

find, look at the distribution of the population and the conditions, and then

slot in the population statistic or its estimator. The value c depends on the

level of confidence

Population

statistic

Population

distribution

Conditions Confidence interval

μ Normal

You know what σ

n is large or small

x is the sample mean

(

x - c

, x + c

)

n n

μ Non-normal

You know what σ

n is large (at least 30)

x is the sample mean

(

x - c

, x + c

)

n n

μ Normal or non-normal

You don’t know what σ

n is large (at least 30)

x is the sample mean

is the sample variance

(

x - c

, x + c

)

n n

p Binomial n is large

is the sample proportion

is 1 - p

(

- c

, p

+ c

)

n n

Level of confidence Value of c

90% 1.64

95% 1.96

99% 2.58

The value of c depends on the level of

confidence you need. These values work

whenever you use the normal distribution

as the basis of your test statistic.

What’s the interval in general?

In general, the confidence interval is given by

statistic ± (margin of error)

The margin of error is given by the value of c multiplied

by the standard deviation of the test statistic.

margin of error = c

(standard deviation of statistic)

confidence interval cheat sheet

you are here 4 505

constructing confidence intervals

Mighty Gumball took a sample of 50 gumballs and found that in the sample, the proportion of red

gumballs is 0.25. Construct a 99% confidence interval for the proportion of red gumballs in the

population.

506 Chapter 12

Mighty Gumball took a sample of 50 gumballs and found that in the sample, the proportion of red

gumballs is 0.25. Construct a 99% confidence interval for the proportion of red gumballs in the

population.

- c

, p

+ c

n n

The confidence interval for the population proportion is given by

We need to find the 99% confidence interval so c = 2.58. The proportion of red gumballs is 0.25, so

= 0.25 and q

= 0.75. n = 50. This gives us

- c

, p

+ c

n n

0.25 - 2.58

0.25 x 0.75

, 0.25 + 2.58

0.25 x 0.75

50 50

= (0.25 - 2.58 x 0.0612, 0.25 + 2.58 x 0.0612)

= (0.25 - 0.158, 0.25 + 0.158)

= (0.092, 0.408)

exercise solution

(

( (

)

) )

you are here 4 507

constructing confidence intervals

When we found the expectation

and variance for X earlier, why did we

substitute in the point estimator for σ

and not μ?

A: We didn’t substitute x for μ because

we needed to find the confidence interval

for μ. We needed to find some sort of

expression involving μ that we could use to

find the confidence interval.

Why did we use x as the value of

A: The distribution of X is the sampling

distribution of means. You form it by taking

every possible sample of size n from the

population, and then forming a distribution

out of all the sample means.

x is the particular value of the mean taken

from our sample, so we use it to help us find

the confidence interval.

What’s the difference between the

confidence interval and the confidence

level?

A: The confidence interval is the

probability that your statistic is contained

within the confidence interval. It’s normally

given as a percentage, for example, 95%.

The confidence interval gives the lower and

upper limit of the interval itself, the actual

range of numbers.

We’ve found that the 95%

confidence interval for μ is (61.72, 63.68).

What does that really mean?

A: What it means is that if you were to

take many samples of the same size and

construct confidence intervals for all of them,

then 95% of your confidence intervals would

contain the true population mean. You know

that 95% of the time, a confidence interval

constructed in this way will contain the

population mean.

In the shortcuts, do the values of c

apply to every confidence interval?

A: They apply to all of the shortcuts

we’ve shown you so far because all of

these shortcuts are based on the normal

distribution. This is because the sampling

distribution in all of these cases follows the

normal distribution.

I’ve sometimes seen “a” instead

of “c” in the shortcuts for the confidence

intervals. Is that wrong?

A: Not at all. The key thing is that whether

you refer to it as “a” or “c”, it represents

a value that you can substitute into your

confidence interval to give you the right

confidence level. The values stay the same

no matter what you call it.

So are all confidence intervals

based on the normal distribution?

A: No, they’re not. We’ll look at intervals

based on other distributions later on.

Why did we go through all those

steps when all we have to do is slot

values into the shortcuts?

A: We went through the steps so that you

could see what was going on underneath

and understand how confidence intervals

are constructed. Most of the time, you’ll just

have to substitute in values.

Do I need continuity corrections

when I’m working with confidence

intervals?

A: Theoretically, you do, but in practice,

they’re generally omitted. This means

that you can just substitute values into

the shortcuts to come up with confidence

intervals.

I have one more

problem I need your

help with. Think you can

help me out?

508 Chapter 12

Just one more problem...

Mighty Gumball has one last problem for you to sort out. One of the

candy stores selling gumballs wants to determine how much gumballs

typically weigh, as they find that their customers often buy gumballs

based on weight rather than quantity. If the store can figure out the

typical weight of a gumball, they can use this information to boost sales.

Mighty Gumball has taken a representative sample of 10

gumballs and weighed each one. In their sample, x = 0.5 oz and

= 0.09.

How do we find the confidence interval?

Assuming the weight of each gumball in the population follows a normal

distribution, how would you go about creating a 95% confidence interval for

this data? Hint: look at the table of confidence interval shortcuts and see which

situation we have here.

Step 1: Choose your population statistic

The first step is to pick the statistic we want to construct a confidence

interval for. We want to construct a confidence interval for the mean

weight of gumballs, so we need to construct a confidence interval for the

population mean, μ.

As we need to find the confidence interval for μ, this means that the next

step is to find its sampling distribution, the distribution of X.

That means I need you to come up with

a confidence interval for gumball weight,

but as it’s just for one store, I don’t want

to sample a large number of gumballs.

confidence interval dilemma: part deux

you are here 4 509

constructing confidence intervals

That’s easy. X is normal, so

that means that X has to follow

a normal distribution, too.

The normal distribution isn’t a good approximation

for every situation.

All of the sampling distributions we’ve seen so far either follow a

normal distribution or can be approximated by it. The trouble is that

we can’t use the normal distribution for every single confidence interval.

Unfortunately, this situation is one of them.

So why can’t we use the normal distribution here?

When sample sizes are large, the normal distribution is ideal for finding

confidence intervals. It gives accurate results, irrespective of how the

population itself is distributed.

Here we have a different situation. Even though X itself is distributed

normally, X isn’t.

So what’s the distribution of X?

There are two key reasons.

The first is that we don’t know what the true variance is of the

population, so this means we have to estimate σ

using the

sample data. We can easily do this using point estimators, but

there’s a problem: the size of the sample is so small that there are

likely to be significant errors in our estimate, much larger errors

than if we used a larger sample of gumballs. The potential errors

we’re dealing with mean that the normal distribution won’t give

us accurate enough probabilities for X, which means it won’t give

us an accurate confidence interval.

So what sort of distribution does X follow? It actually follows a

t-distribution. Let’s find out more.

But why not?

That doesn’t

make sense to me.

Step 2: Find its sampling distribution

510 Chapter 12

The t-distribution

The exact shape of the t-

distribution depends on the size

of the sample and the value of ν.

The two are related.

T ~ t(ν)

Small values of

ν always make

my tail look big.

The t-distribution is a probability distribution that specializes in exactly the

sort of situation we have here. It’s the distribution that X follows where the

population is normal, σ

is unknown, and you only have a small sample at

your disposal.

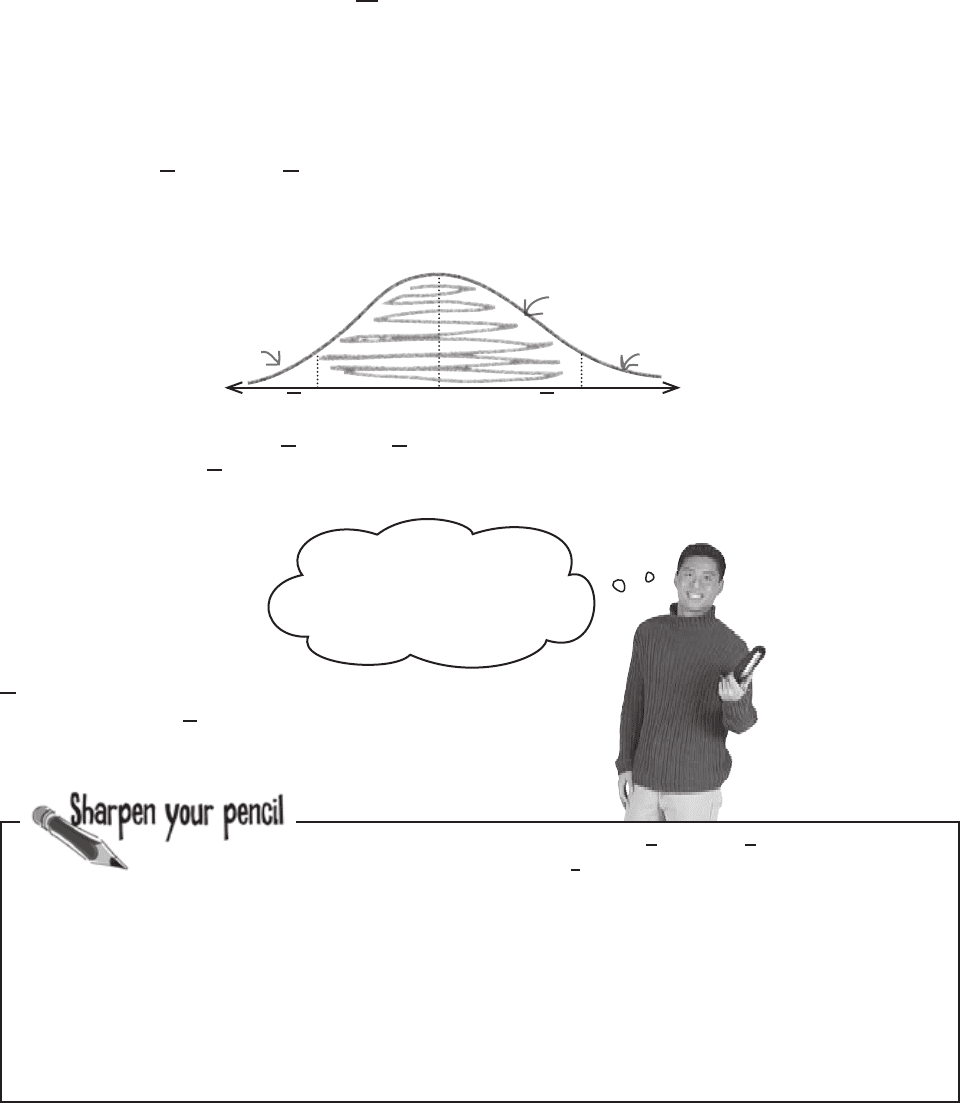
The t-distribution looks like a smooth, symmetrical curve, and it’s exact

shape depends on the size of the sample. When the sample size is large, it

looks like the normal distribution, but when the sample size is small, the

curve is flatter and has slightly fatter tails. It takes one parameter, ν, where

ν is equal to n – 1. n is the size of the sample, and ν is called the number

of degrees of freedom.

Let’s take a look at this. Here’s a sketch of the t-distribution for different

values of ν. Can you see how the value of ν affects the shape of the

distribution?

A shorthand way of saying that T follows the t-distribution with ν

degrees of freedom is

t(ν) means we’re using the t-distribution

with ν degrees of freedom. ν = n - 1.

The t-distribution works in a similar way to the normal distribution. We

start off by converting the limit of the probability area into a standard

score, and then we use probability tables to get the result we want.

Let’s start with the standard score.

large v

small v

T is the test statistic. You’ll see how

to calculate it on the next page

introducing t-distributions

X follows the t-distribution when the sample is small

We’ll look at degrees of

freedom in more depth

in Chapter 14.