Griffiths D. Head First Statistics

Подождите немного. Документ загружается.

you are here 4 511

constructing confidence intervals

We calculate the standard score for the t-distribution in the same way we

did for the normal distribution. As with the the normal distribution, we

standardize by subtracting the expectation of the sampling distribution

and then dividing by its standard deviation. The only difference is that

we represent the result with T instead of Z, as we’re going to use it with

the t-distribution.

We need to find the distribution of X, so this means we need to use the

expectation and standard deviation of X. The expectation of X is μ, and

the standard deviation is σ/n. As we need to estimate the value of σ

with s, this means that the standard score for the t-distribution is given by

This is the standard deviation of X.

This is the same formula as for

Z—subtract the mean and divide

by the standard deviation.

This is the population mean we’re

finding a confidence interval for.

Let’s see if you can apply this to the Mighty Gumball

sample. There are 10 gumballs in the sample, where

x = 0.5oz and s

= 0.09. What’s the value of ν and

what’s T?

All we need to do is substitute in the values for X, , and n.

T = X - μ

s/√n

Find the standard score for the t-distribution

512 Chapter 12

Step 3: Decide on the level of confidence

So what level of confidence should we use for Mighty Gumball?

Remember, the level of confidence says how sure you want to be that

the confidence interval contains the population statistic, and it helps us

figure out how wide the confidence interval needs to be. As before, let’s

have a confidence level of 95% for the population mean. This means

that the probability of the population mean being inside the confidence

interval is 0.95.

For a confidence level of 95%, the

probability here is 0.95.

Now that we have the level of confidence, we can move onto the final

step, finding the confidence interval for μ.

There are 10 gumballs in the sample, and ν = n - 1. This means that the value of ν is 9.

T is given by

T = X - μ

s/√n

= X - μ

√0.09/10

= X - μ

0.0949

Let’s see if you can apply this to the Mighty Gumball

sample. There are 10 gumballs in the sample, where

x = 0.5oz and s

= 0.09. What’s the value of ν, and

what’s T?

μ = x

sharpen solution

you are here 4 513

constructing confidence intervals

Using t-distribution probability tables

t-distribution probability tables give you the value of t where

P(T > t) = p. In our case, p = 0.025.

To find t, use the first column to look up ν, and the top row to look up

p. The place where they intersect gives the value of t. As an example,

if we look up ν = 7 and p = 0.05, we get t = 1.895.

Once you’ve found the value of t, you can use it to find your

confidence interval.

Step 4: Find the confidence limits

You find confidence limits with the t-distribution in a similar way to

how you find them with the normal distribution. Your confidence

interval is given by

(

x - t

, x + t

)

√n √n

where

P(-t ≤ T ≤ t) = 0.95

We can find the value of t using t-distribution probability tables.

This is the same as we had

before, just replace c with t.

This is 0.95, as we

want to find the 95%

confidence interval.

Tail probability p

.25 .20 .15 .10 .05 .025 .02 .01 .005 .0025 .001 .0005

1 1.000 1.376 1.963 3.078 6.314 12.71 15.89 31.82 63.66 127.3 318.3 636.6

2 .816 1.061 1.386 1.886 2.920 4.303 4.849 6.965 9.925 14.09 22.33 31.60

3 .765 .978 1.250 1.638 2.353 3.182 3.482 4.541 5.841 7.453 10.21 12.92

4 .741 .941 1.190 1.533 2.132 2.776 2.999 3.747 4.604 5.598 7.173 8.610

5 .727 .920 1.156 1.476 2.015 2.571 2.757 3.365 4.032 4.773 5.893 6.869

6 .718 .906 1.134 1.440 1.943 2.447 2.612 3.143 3.707 4.317 5.208 5.959

7 .711 .896 1.119 1.415 1.895 2.365 2.517 2.998 3.499 4.029 4.785 5.408

8 .706 .889 1.108 1.397 1.860 2.306 2.449 2.896 3.355 3.833 4.501 5.041

9 .703 .883 1.100 1.383 1.833 2.262 2.398 2.821 3.250 3.690 4.297 4.781

10 .700 .879 1.093 1.372 1.812 2.228 2.359 2.764 3.169 3.581 4.144 4.587

p = 0.05

This is where 7 and .05 meet.

ν = 7

-t

T ~ t(ν)

0.95

0.025

T ~ t(ν)

514 Chapter 12

See if you can find the 95% confidence interval for the average weight of gumballs.

There are 10 gumballs in the sample where x = 0.5oz and s

= 0.09.

1. The confidence interval for μ is given by (x - t s/√n, x + t s/√n).

Use standard probability tables to find the value of t.

2. Use this to find the confidence interval for μ.

confidence interval exercise

you are here 4 515

constructing confidence intervals

The t-distribution vs. the normal distribution

So why did we use the

t-distribution for this problem?

Why couldn’t we have used the

normal distribution instead?

The t-distribution is more accurate when we

have to estimate the population variance for

small samples.

The problem with basing our estimate of σ

on just a small

sample is that it may not accurately reflect the true value of

the population variance. This means we need to make some

allowance for this in our confidence interval by making the

interval wider.

The shape of the t-distribution varies in line with the value of

ν. As it takes the size of the sample into account, this means that

it allows for any uncertainty we may feel about the accuracy of

our estimate for σ

. When n is small, the t-distribution gives a

wider confidence interval than the normal distribution, which

makes it more appropriate for small-sized samples.

Handy shortcuts for confidence intervals - the t-distribution

Here’s a quick reminder of when you need to use the t-distribution, and what the

confidence interval is for μ. Just substitute in your values.

To find t(ν), you need to look it up in t-distribution probability tables. To do this, use

ν = n - 1 and your level of confidence to find the critical region.

Population

statistic

Population

distribution

Conditions Confidence interval

μ Normal or non-normal

You don’t know what σ

n is small (less than 30)

x is the sample mean

is the sample variance

(

x - t(ν)

, x + t(ν)

)

√n √n

516 Chapter 12

See if you can find the 95% confidence interval for the average weight of gumballs.

There are 10 gumballs in the sample where x = 0.5oz and s

= 0.09.

exercise solution

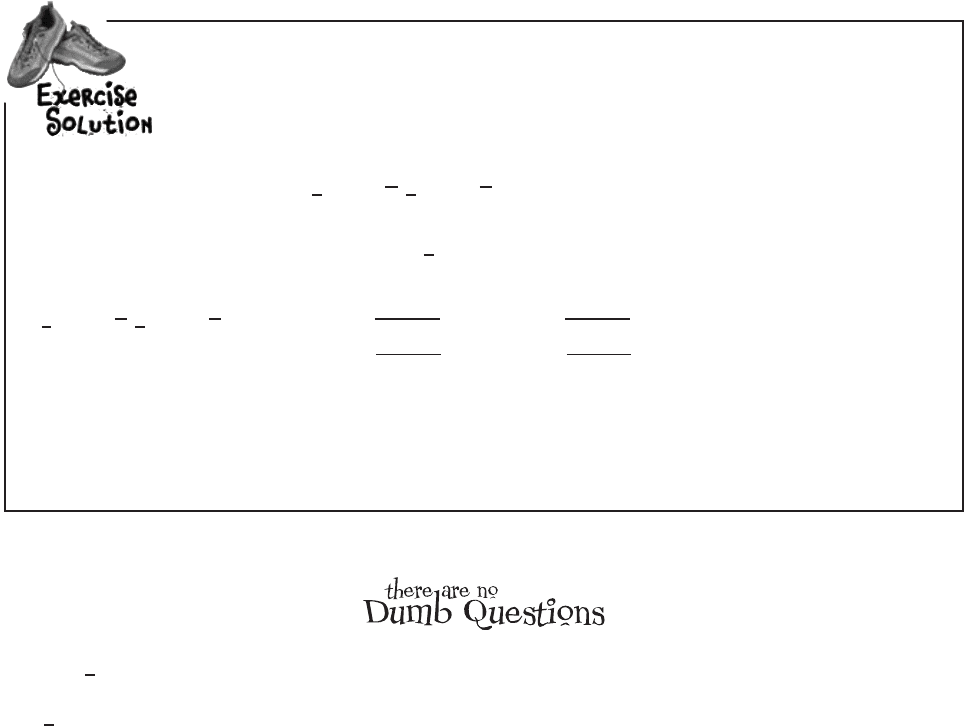
We find the confidence interval by substituting values for x, t, s, and n into (x - t s/√n, x + t s/√n).

This gives us

(x - t s/√n, x + t s/√n) = (0.5 - 2.262 x √(0.09/10), 0.5 + 2.262 x √(0.09/10))

= (0.5 - 2.262 x 0.0949, 0.5 + 2.262 x 0.0949)

= (0.5 - 0.215, 0.5 + 0.215)

= (0.285, 0.715)

1. The confidence interval for μ is given by (x - t s/√n, x + t s/√n).

Use standard probability tables to find the value of t.

There are 10 gumballs in the sample, so ν = 9. We want to find the 95% confidence interval, so this means

we look up 0.025 in the t-distribution probability table, with 9 degrees of freedom. This gives us t =

2.262.

2. Use this to find the confidence interval for μ.

you are here 4 517

constructing confidence intervals

Mighty Gumball has noticed a problem with their gumball dispensers. They have taken a sample

of 30 machines, and found that the mean number of malfunctions is 15. Construct a 99%

confidence interval for the number of malfunctions per month.

518 Chapter 12

Mighty Gumball has noticed a problem with their gumball dispensers. They have taken a sample

of 30 machines, and found that the mean number of malfunctions is 15. Construct a 99%

confidence interval for the number of malfunctions per month.

Does X follow a t-distribution?

X follows a t-distribution when the population is normal, the

sample size is small, and you need to estimate the population

variance using the sample data.

In general, what happens to my confidence interval if the

confidence level changes?

A: If your confidence level goes down, then your confidence

interval gets narrower. If your confidence level goes up, then your

confidence interval gets wider. As an example, a 95% confidence

interval will be narrower than a 99% confidence interval for the same

set of data.

What happens to the confidence interval if the size of the

sample, n, changes?

A: If n decreases, then your confidence interval gets wider, and if

n increases, your confidence interval gets narrower.

Confidence intervals take the form

tatistic ± margin of error

where the margin of error is equal to c times the standard deviation

of the statistic.

The standard deviation of the statistic depends on the size of the

sample, and it gets smaller as n gets larger. In other words, the

margin of error gets smaller as n gets larger, and larger as n gets

smaller.

In general, a smaller sample leads to a wider confidence interval, and

a larger sample to a narrower one.

exercise solution

The number of breakdowns per month is modelled by a Poisson distribution. As there are 30 machines, we can

find the confidence interval using (x - cs/√n, x + cs/√n).

We need to find the 99% confidence interval, which means that c = 2.58. For the poisson distribution, the

expectation and variance are both equal to λ, so x = 15 and s

= 15.

The confidence interval is given by

(x - cs/√n, x + cs/√n) = (15 - 2.58 x √(15/30), 15 + 2.58 x √(15/30))

= (15 - 2.58 x √

(15/30), 15 + 2.58 x √(15/30))

= (15 - 2.58 x 0.707, 15 + 2.58 x 0.707)

= (15 - 1.824, 15 + 1.824)

= (13.176, 16.824)

you are here 4 519

constructing confidence intervals

You’ve found the confidence intervals!

You’ve made a lot of progress in this chapter, and the result of it is

that you now know two ways of estimating population statistics.

The first way of estimating population statistics is to use point

estimators. Point estimators give you a way of estimating the

precise value for the population statistics. It’s the best guess you can

possibly make based on the sample data.

You also know how to come up with confidence intervals for

the population statistics. Rather than come up with a very precise

estimate for the population statistics, you now know how to find a

range of values for the population statistic that you can feel truly

confident about.

You’re great! I’ll tell the candy shop what the

confidence interval is for the mean weight of

gumballs, as that’s just what they wanted to

know. They’ll be able to sell more gumballs to their

customers, and that means increased profits!