Griffiths D. Head First Statistics

Подождите немного. Документ загружается.

you are here 4 541

using hypothesis tests

Hypothesis Magnets

It’s time to do another hypothesis test. There are a number of steps

you need to run through to perform the hypothesis test, but can you

remember what the order is? Put the magnets into the right order.

Decide on the hypothesis you’re going to test

See whether the test statistic is within the critical region

Find the p-value of the test statistic

Choose your test statistic

Determine the critical region for your decision

Make your decision

542 Chapter 13

Hypothesis Magnets Solution

It’s time to do another hypothesis test. There are a number of steps

you need to run through to perform the hypothesis test, but can you

remember what the order is? Put the magnets into the right order.

Decide on the hypothesis you’re going to test

See whether the test statistic is within the critical region

Find the p-value of the test statistic

Choose your test statistic

Determine the critical region for your decision

Make your decision

hypothesis magnets solution

you are here 4 543

using hypothesis tests

nore

ull

nore

ull

48 T

ableTS

Step 1: Decide on the hypotheses

We need to start off by finding the null hypothesis and alternate

hypothesis of the SnoreCull trial. As a reminder, the null hypothesis is the

claim that we’re testing, and the alternate hypothesis is what we’ll accept if

there’s sufficient evidence against the null hypothesis.

So what are the null and alternate hypotheses?

It’s still the same problem

For the last test, we took the claims made by the drug company and used

these as the basis for the null hypothesis. We’re testing the same claims, so the

null hypothesis is still the same. We have

: p = 0.9

: p < 0.9

The alternate hypothesis is the same too. If there is strong evidence

against the claims made by the drug company, then we’ll accept that the

drug cures fewer than 90% of the patients. This gives us an alternate

hypothesis of:

So you still don’t

believe me? Think you

can have another shot

at me? Bring it on!

Let’s conduct another hypothesis test

The doctor still has misgivings about the claims made by the drug company.

Let’s conduct a hypothesis test based on the new data.

Decide on the

hypothesis you’re going

to test

Choose your test

statistic

Determine the critical

region for your decision

Find the p-value of the

test statistic

See whether the

sample result is within

the critical region

Make your decision

544 Chapter 13

As before, the next step is to choose the test statistic. In other words, we

need some statistic that we can use to test the hypothesis.

For the previous hypothesis test, we conducted the test by looking at the

number of successes in the sample and seeing how significant the result

was. We used the binomial distribution to find the probability of getting a

result at least as extreme as the value we got in the sample. In other words,

we used a test statistic of X ~ B(15, 0.9) to test whether P(X 11) was less

than 0.05, the level of significance.

This time the number of people in the sample is 100, and we’re testing

the same claim, that probability of successfully curing someone is 0.9.

This means that our new test statistic is X ~ B(100, 0.9).

Step 2: Choose the test statistic

Are you kidding me?

If we have to calculate

probabilities using the

binomial distribution, we’ll

be here forever.

We can use another probability distribution instead

of the binomial.

Using the binomial distribution for this sort of problem would be time

consuming, as we’d have to calculate lots of probabilities.

Fortunately, there’s another way. Rather than use the binomial

distribution, we can use some other distribution instead.

What probability distribution could you use to approximate X ~ B(100, 0.9)?

Decide on the

hypothesis you’re going

to test

Choose your test

statistic

Determine the critical

region for your decision

Find the p-value of the

test statistic

See whether the

sample result is within

the critical region

Make your decision

pick the test statistic

you are here 4 545

using hypothesis tests

To get the most out of hypothesis tests, you need to know how different variables and

parameters are distributed. What distributions would you use to find probabilities for the

following situations?

1. X ~ B(n, p). What probability distribution could you use to approximate this if n is large, np > 5 and nq > 5?

2. X ~ N(μ, σ

). You know the value of μ and σ

. What’s the distribution of X?

3. X ~ N(μ, σ

), and you know what μ is, but you don’t know what the value of σ

is. The sample size is large. What’s

the distribution of X given the data you have?

4. X ~ N(μ, σ

), you know what μ is, but you don’t know what the value of σ

is. The sample size is small. What’s the

distribution of X given the data you have?

Hint: We covered all of these earlier in

the book. If you get stuck, look back

through the chapters

546 Chapter 13

To get the most out of hypothesis tests, you need to know how different variables and parameters

are distributed. What distributions would you use to find probabilities for the following situations?

Hint: We covered all of these earlier in the book. If you get stuck, look back through the chapters.

1. X ~ B(n, p). What probability distribution could you use to approximate this if n is large, np > 5 and nq > 5?

If n is large, then we can approximate X ~ B(n, p) using the normal distribution. As E(X) = np and

Var(X) = npq, this means we can use X ~ N(np, npq). This assumes that np > 5 and nq > 5.

2. X ~ N(μ, σ

). You know the value of μ and σ

. What’s the distribution of X?

3. X ~ N(μ, σ

), and you know what μ is, but you don’t know what the value of σ

is. The sample size is large. What’s

the distribution of X given the data you have?

If we know what the value is of σ

, X ~ N(μ, σ

/n).

If we don’t know what the value is of σ

, we estimate it using s

. So, X ~ N(μ, s

/n).

4. X ~ N(μ, σ

), you know what μ is, but you don’t know what the value of σ

is. The sample size is small. What’s the

distribution of X given the data you have?

If we don’t know what the value is of σ

, we estimate it using s

. If the sample size is small, we need to use

the t-distribution T ~ t(n - 1) where T = X - μ

s/√n

exercise solution

you are here 4 547

using hypothesis tests

We still need to find a test statistic we can use in our hypothesis test, and

as the number in the sample is large, this means that using the binomial

distribution will be time consuming and complicated.

There are 100 people in the sample, and the proportion of successes

according to the drug company is 0.9. In other words, the number of

successes follows a binomial distribution, where n = 100 and p = 0.9.

As n is large, and both np and nq are greater than 5, we can use

X ~ N(np, npq) as our test statistic, where X is the number of patients

successfully cured. In other words, we can use

X ~ N(90, 9)

to approximate any probabilities that we may need.

If we standardize this, we get

This means that for our test statistic we can use

Z = X - 90

Z ~ N(0, 1)

Here we’re standardizing

X ~ N(90, 9).

I get it. So our test

statistic is the variable

we use for our test.

You use the test statistic to work out probabilities

you can use as evidence.

This means that we use Z as our test statistic, as we can easily use it to

look up probabilities and see how unlikely the results of our sample

are given the claims of the drug company. We substitute our value of

80 in place of X, so we can use it to find the probability of 80 or fewer

being cured.

Use the normal to approximate the binomial in our test statistic

Z = X - 90

= X - 90

We can use this because n is

large, np > 5 and nq is large.

X is the number of patients

cured, in our case 80.

548 Chapter 13

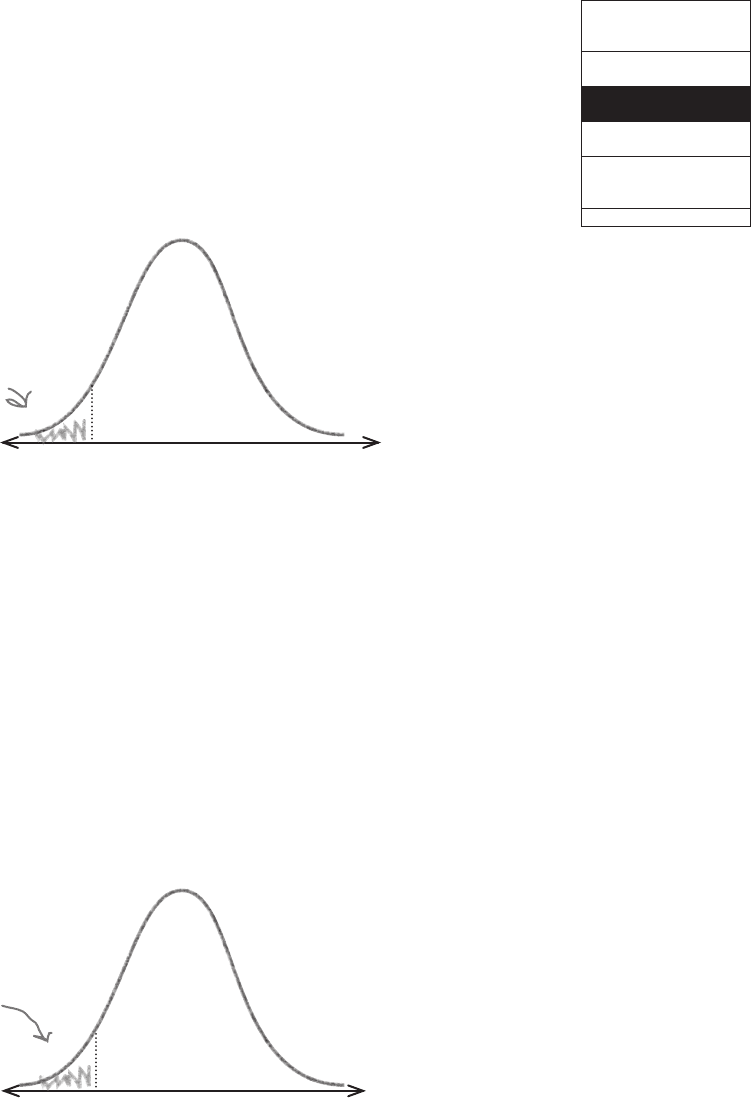
Step 3: Find the critical region

Now that we have a test statistic for our test, we need to come up

with a critical region. As our alternate hypothesis is p < 0.9, this

means that our critical region lies in the lower tail just as before.

The critical region also depends on the significance level of the

test. Let’s choose the same significance level as before, so let’s test

at the 5% level.

As our test statistic follows a standard normal distribution, we

can use probability tables to find the critical value, c. The critical

value is the boundary between whether we have strong enough

evidence to reject the null hypothesis or not.

As our significance level is 5%, this means that our critical

value c is the value where P(Z < c) = 0.05. If we look up the

probability 0.05 in the probability tables, this gives us a value for

c of -1.64. In other words,

Z ~ N(0, 1)

P(Z < -1.64) = 0.05

This means that if our test statistic is less than -1.64, we have strong

enough evidence to reject the null hypothesis.

If the test statistic lies

in this region, then there’s

enough evidence to reject

the null hypothesis

Decide on the

hypothesis you’re going

to test

Choose your test

statistic

Determine the critical

region for your decision

Find the p-value of the

test statistic

See whether the

sample result is within

the critical region

Make your decision

-1.64

Z ~ N(0, 1)

find another critical region

you are here 4 549

using hypothesis tests

Think you can go through the remaining steps of the hypothesis test? See if you can find the

following:

Step 4: Find the p-value

The critical region is in the lower tail of the distribution. 80 people were cured,

and Z = (X - 90)/3. Use this to find the p-value.

Step 5: See whether the test statistic is within the critical region

Remember that the significance level for the hypothesis test is 5%.

Step 6: Make your decision

Do you accept or reject the null hypothesis based on the evidence?

550 Chapter 13

Think you can go through the remaining steps of the hypothesis test? See if you can find the

following:

Step 4: Find the p-value

The critical region is in the lower tail of the distribution. 80 people were cured,

and Z = (X - 90)/3. Use this to find the p-value.

Let’s start by finding the standard score of 80.

z = (80 - 90)/3

= -10/3

= -3.33

The p-value is given by P(Z < z) = P(Z < -3.33). Looking this up in probability tables gives us

p-va

lue = 0.0004

Step 5: See whether the test statistic is within the critical region

Remember that the significance level for the hypothesis test is 5%.

The test statistic is on the critical region if the p-value is less than 0.05. As the p-value is equal

to 0.0004, this means that the test statistic is within the critical region.

Step 6: Make your decision

Do you accept or reject the null hypothesis based on the evidence?

As the test statistic is within the critical region for the hypothesis test, this means that we have

sufficient evidence to reject the null hypothesis at the 5% significance level.

exercise solution