Griffiths D. Head First Statistics

Подождите немного. Документ загружается.

you are here 4 561

using hypothesis tests

Introducing power

So far we’ve looked at the probability of getting different types of error in

our hypothesis test. One thing that we haven’t looked at is power.

The power of a hypothesis test is the probability that we will reject H

when H

is false. In other words, it’s the probability that we will make the

correct decision to reject H

That sounds complicated. I

hope it’s not as difficult to

find as P(Type II error).

Once you’ve found P(Type II error), calculating the

power of a hypothesis test is easy.

Rejecting H

when H

is false is actually the opposite of making a Type II

error. This means that

Power = 1 - β

where β is the probability of making a Type II error.

So what’s the power of SnoreCull?

We’ve found the probability of getting a Type II error is 0.102. This

means that we can find the power of the SnoreCull hypothesis test by

calculating

Power = 1 - P(Type II error)

= 1 - 0.102

= 0.898

In other words, the power of the SnoreCull hypothesis test is 0.898. This

means that the probability that we will make the correct decision to reject

the null hypothesis is 0.898.

562 Chapter 13

The doctor’s happy

In this chapter, you’ve run through two hypothesis tests, and

you’ve proved that there’s sufficient evidence to reject the claims

made by the drug company. You’ve been able to show that based

on the doctor’s sample, there’s sufficient evidence that SnoreCull

doesn’t cure 90% of snorers, as the drug company claims.

I thought that the claims sounded too

good to be true, and you’ve proved that

there are strong statistical grounds

for showing I’m right. I’ll sleep quieter

at night knowing that.

But it doesn’t stop there

Keep reading, and we’ll show you what

other sorts of hypothesis tests you can use.

We’ll see you over at Fat Dan’s Casino...

nore

ull

nore

ull

48 T

ableTS

snorecull is a fraud!

you are here 4 563

using hypothesis tests

The drug company and their cough syrup manufacturer are having a dispute. The factory says

that the amount of syrup that gets poured into their bottles follows a distribution

X ~ N(355, 25), where X is the amount of syrup in the bottle measured in mL. The drug company

conducted tests on a large sample and found that the mean amount of syrup in 100 bottles

is 356.5 mL. Test the hypothesis that the factory mean is correct at a 1% level of significance

against the alternative that the mean amount of syrup in a bottle is greater than 355 mL.

We’re going to guide you through this exercise in two parts. Here are the first three steps.

Step 1: Decide on the hypothesis you’re going to test. What’s the null hypothesis? What’s the alternate

hypothesis?

Step 2: Choose your test statistic.

Step 3: Determine the critical region for your decision. Does the critical region lie in the lower or upper tail of the

distribution? What’s the significance level? What’s the critical value?

Hint: Your hypothesis concerns the mean,

so what’s the distribution of X? How

do you standardize this?

(part 1)

X ~ N(μ, σ

/n), so this means that under the null hypothesis, X ~ N(355, 25/100) or X ~ N(355, 0.25).

If we standardize this, we get

Z = X - 355

0.25

= X - 355

0.5

Step 1: Decide on the hypothesis you’re going to test. What’s the null hypothesis? What’s the alternate

hypothesis?

We want to test whether the mean amount of syrup in the bottles is 355 mL like the factory says. This

gives us

: μ = 355

: μ > 355

Step 2: Choose your test statistic.

Step 3: Determine the critical region for your decision. Does the critical region lie in the lower or upper tail of the

distribution? What’s the significance level? What’s the critical value?

The alternate hypothesis is μ > 355, which means the critical region lies in the upper tail. We want to test

at the 1% significance level, so the critical region is defined by P(Z > c) = 0.01. Using probability tables,

this gives us c = 2.32. In other words, the critical region is given by Z > 2.32.

The drug company and their cough syrup manufacturer are having a dispute. The factory says

that the amount of syrup that gets poured into their bottles follows a distribution

X ~ N(355, 25), where X is the amount of syrup in the bottle measured in mL. The drug company

conducted tests on a large sample and found that the mean amount of syrup in 100 bottles

is 356.5 mL. Test the hypothesis that the factory mean is correct at a 1% level of significance

against the alternative that the mean amount of syrup in a bottle is greater than 355 mL.

We’re going to guide you through this exercise in two parts. Here are the first three steps.

(part 1)

564 Chapter 13

exercise solution

you are here 4 565

using hypothesis tests

This exercise continues where the last left off. Here are the final three steps of the hypothesis

test. What do you conclude?

Step 4: Find the p-value of the test statistic. Use the distribution Z = (X - 355)/0.5, the mean amount of syrup in

the sample, and remember that this time you’re seeing if your test statistic lies in the upper tail of the distribution, as

this is where the critical region is.

Step 5: See whether the sample result is within the critical region. Remember that you’re testing at the 1%

significance level.

Step 6: Make your decision. Is there enough evidence to reject the null hypothesis at the 1% level of significance?

(part 2)

566 Chapter 13

This exercise follows on from the last. Here are the final three steps of the hypothesis test. What

do you conclude?

Step 4: Find the p-value of the test statistic. Use the distribution Z = (X - 355)/0.5, the mean amount of syrup in the

sample, and remember that this time you’re seeing if your test statistic lies in the upper tail of the distribution as this

is where the critical region is.

Z = (X - 355)/0.5

= (356.5 - 355)/0.5

= 1.5/0.5

= 3

The p-value for this is given by P(Z > 3), as the critical region is in the upper tail. Looking this up in

probability tables gives us

p-value = 0.0013

Step 5: See whether the sample result is within the critical region. Remember that you’re testing at the 1%

significance level.

The p-value 0.0013 is less than 0.01, the significance level, so that means that the sample result is within

the critical region

Step 6: Make your decision. Is there enough evidence to reject the null hypothesis at the 1% level of significance?

As the sample result lies in the critical region, there’s sufficient evidence to reject the null hypothesis. We

can accept the alternate hypothesis that μ > 355 ml.

A Type I error is when you reject the null hypothesis when it’s actually

correct. The probability of getting a Type I error is α, the significance level of

the test.

A Type II error is when you accept the null hypothesis when it’s wrong. The

probability of getting a Type II error is represented by β.

To find β, your alternate hypothesis must have a specific value. You then

find the range of values outside the critical region of your test, and then find

the probability of getting this range of values under H



exercise solution

(part 2)

this is a new chapter 567

the χ

distribution

There’s Something

Going On...

Sometimes things don’t turn out quite the way you expect.

When you model a situation using a particular probability distribution, you have a

good idea of how things are likely to turn out long-term. But what happens if there are

differences between what you expect and what you get? How can you tell whether

your discrepancies come down to normal fluctuations, or whether they’re a sign of

an underlying problem with your probability model instead? In this chapter, we’ll

show you how you can use the χ

distribution to analyze your results and sniff out

suspicious results.

I thought his success

with girls would follow a

binomial distribution with

p = 0.8. I was so wrong...

568 Chapter 14

Fat Dan’s is used to making a tidy profit from its

casino-goers, but this week there’s a problem. The slot

machines keep hitting the jackpot, the roulette wheel

keeps landing on 12, the dice are loaded, and too many

people are winning off one of the blackjack tables.

The casino can’t support the loss for much longer, and

Fat Dan suspects foul play. He needs your help to get

to the bottom of what’s going on.

There may be trouble ahead at Fat Dan’s Casino

could fat dan’s casino be rigged?

you are here 4 569

the χ

distribution

Let’s start with the slot machines

As you’ve seen before, Fat Dan’s Casino has a full row of bright, shiny slot

machines, just waiting to be played. The trouble is that people keep on playing

them—and winning.

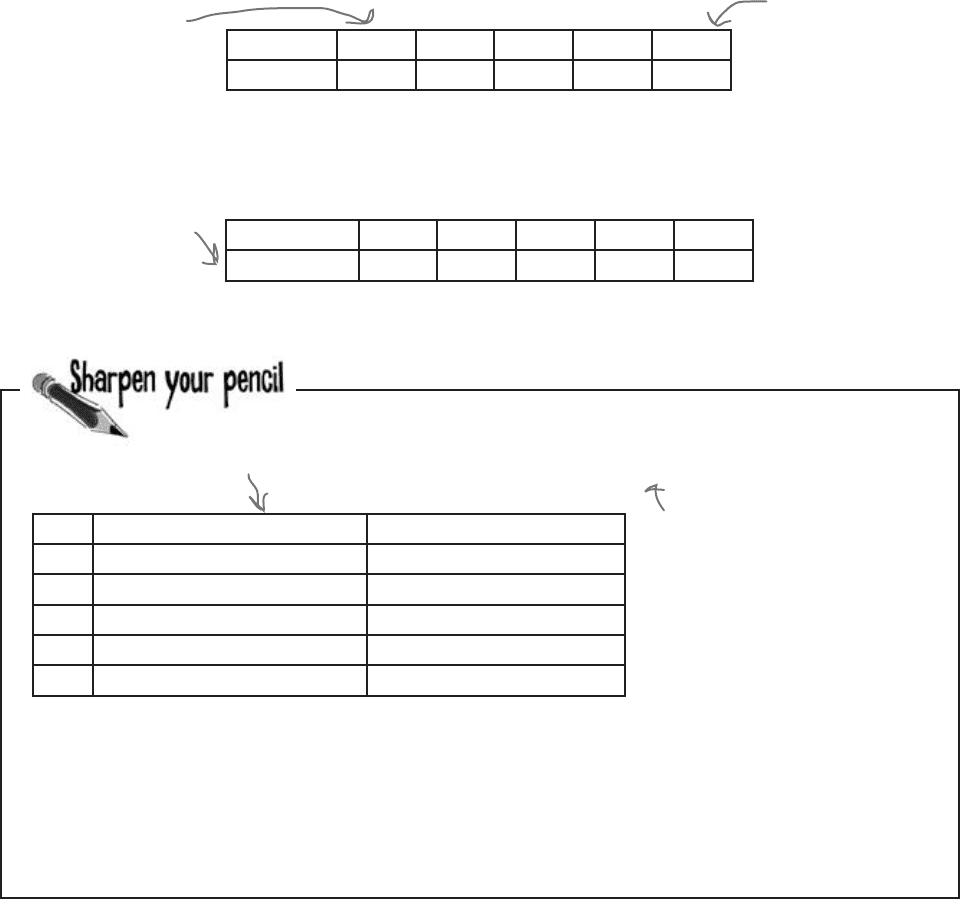
Here’s the expected probability distribution for one of the slot machines, where X

represents the net gain from each game played:

The casino has collected statistics showing the number of times people get each

outcome. Here are the frequencies for the observed net gains per game:

We need to compare the actual frequency of each value of x with

what you’d expect the frequency to be based on the probability

distribution. Fill in the table below. What do you notice?

x -2 23 48 73 98

P(X = x)

0.977 0.008 0.008 0.006 0.001

x -2 23 48 73 98

Frequency

965 10 9 9 7

x Observed frequency Expected frequency

-2

965 977

The observed frequency

is what we actually get.

Hint: The total observed frequency is

1000, as this is what you get if you

add all the observed frequencies. Use

the probability distribution to work

out what you’d expect the frequencies

to be.

It’s $2 per game, so if

you don’t win anything,

you lose your $2.

If you hit the jackpot,

your net gain is $98.

The frequency shows

you how many games had

which net gain.

570 Chapter 14

We need to compare the actual frequency of each value of x with

what you’d expect the frequency to be based on the probability

distribution. Fill in the table below. What do you notice?

Looking at the data, it looks

like there might be something

going on with the slot machine

payouts. But how can we be

certain? It’s unlikely, but this

could happen by pure chance.

x Observed frequency Expected frequency

-2

965 977

We need some way of deciding whether these results

show the slot machines have been rigged.

What we need is some sort of hypothesis test that we can use to test the

differences between the observed and expected frequencies. That way, we’ll

have some way of deciding whether the slot machines have been tampered

with to make sure they keep paying out lots of money.

The question is, what sort of distribution can we use for this hypothesis test?

There’s a difference between the number of people you’d expect to win the jackpot, based

on the probability distribution, and the number of people actually winning it. What we don’t

know is how significant these differences are.

We found the expected frequencies

by multiplying the probability of

each outcome by 1000, the total

frequency.

sharpen your pencil solution