Griffiths D. Head First Statistics

Подождите немного. Документ загружается.

you are here 4 591

the χ

distribution

We still need to calculate degrees of freedom

Before we can use the χ

distribution to find the significance of the observed

frequencies, there’s just one more thing we need to find. We need to find ν, the

number of degrees of freedom.

You saw earlier that the number of degrees of freedom is the number of pieces

of independent information we are free to choose, taking into account any

restrictions. This means that we look at how many expected frequencies we have

to calculate independently, and subtract the number of restrictions.

First of all, let’s look at the total number of expected frequencies we had to

calculate. We had to figure out the expected frequencies for the three croupiers

and the three possible outcomes. This means that we worked out 3

3 = 9

expected frequencies.

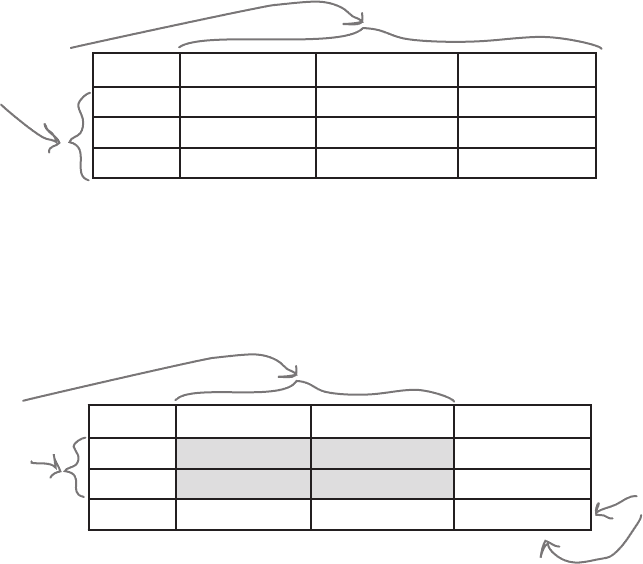
Croupier A Croupier B Croupier C

Win

Draw

Lose

We had to figure out

3x3 = 9 expected

frequencies.

Now for each row and for each column, we only actually had to calculate two of

the expected frequencies. We knew what the total frequency should be, so we could

choose the third to make sure that the frequencies added up to the right result. In

other words, we only actually had to calculate 4 of the expected frequencies; the

other 5 had to fit in with the total frequencies we already knew about.

Croupier A Croupier B Croupier C

Win

Draw

Lose

We only had to calculate these

expected frequencies - we

could figure out the others

using the total frequency of

each row and column.

Since we had to calculate 4 expected frequencies, this makes the number of

degrees of freedom. There were 4 pieces of independent information we had

to calculate; once we’d done that, the rest were known automatically. In other

words, ν = 4.

Another way of looking at this is that we needed to find 9 values overall, and

there were 5 values that we didn’t have to calculate independently. Using our

formula from before, this gives us ν = 9 – 5 = 4.

We could figure

the last row and

column out using

the totals.

592 Chapter 14

Conduct a hypothesis test with a 1% significance level to see whether the outcome of the

game is independent of the croupier manning the table. Here’s a reminder of the steps, but

remember you’ve worked out some of these already.

1. Decide on the hypothesis you’re going to test, and its alternative.

2. Find the expected frequencies and the degrees of freedom.

3. Determine the critical region for your decision.

4. Calculate the test statistic Χ

5. See whether the test statistic is within the critical region.

6. Make your decision.

another long exercise

you are here 4 593

the χ

distribution

We’ve left you lots of space

for your calculations.

594 Chapter 14

Conduct a hypothesis test with a 1% significance level to see whether the outcome of the

game is independent of the croupier manning the table. Here’s a reminder of the steps, but

remember you’ve worked out some of these already.

1. Decide on the hypothesis you’re going to test, and its alternative.

2. Find the expected frequencies and the degrees of freedom.

3. Determine the critical region for your decision.

4. Calculate the test statistic Χ

5. See whether the test statistic is within the critical region.

6. Make your decision.

Step 1:

We want to test whether the outcome of the game is independent of the croupier manning the table. This

means we can use:

: There is no relationship between the outcome of the game and the croupier manning the table.

: There is a relationship between the outcome of the game and the croupier manning the table

Step 2:

We found the expected frequencies in the exercise back on page 590, and we’ve just seen that the number

of degrees of freedom is 4.

Step 3:

From probability tables, χ

(4) = 13.28. This means that the critical region is given by X

> 13.28.

Step 4:

We also calculated the test statistic X

using the expected frequencies back on page 590. We found that

= 5.004.

Step 5:

The critical region is given by X

> 13.28, so this means that X

is outside the critical region.

Step 6:

As X

is outside the critical region, we accept the null hypothesis. There is insufficient evidence that there’s

a relationship between game outcome and croupier.

and another long exercise solution

you are here 4 595

the χ

distribution

Take a look at how we calculated the degrees

of freedom for a 3x3 table. How do you think

we could generalize this? See if you can work

this out, then turn the page.

I’m still not sure I understand how

you found the degrees of freedom for the

croupiers. Why are there four degrees of

freedom?

A: We found the degrees of freedom by

looking at how many expected frequencies

we had to calculate, and working out how

many of these we could have calculated by

just looking at the total observed frequencies

for each row and column.

There are three croupiers and three

outcomes. If you use a contingency table to

calculate these, the row and column totals

for the expected frequencies must match

those of the observed frequencies. This

means that once you’ve calculated the first 2

expected frequencies for any row or column,

the final one is determined by the overall

total. Therefore, you only need to calculate

2×2 expected frequencies from scratch. This

gives you your four degrees of freedom.

Are there any other uses of the χ

distribution besides testing goodness of

fit and independence?

A: These are the two main uses of the

distribution. The thing to remember is

that you can use it to test the goodness of

fit of virtually any probability distribution. As

an example, you can use it to test whether

observed frequencies fit a particular binomial

distribution.

Should I test at any particular

level?

A: It depends on your situation. Just as

with other hypothesis tests, the smaller the

level of significance, the stronger you need

your evidence to be before you reject your

null hypothesis.

Testing at the 5% and 1% level of

significance is common.

I wonder what happens

if you have a different size

contingency table? How

do you find the number of

degrees of freedom then?

596 Chapter 14

Generalizing the degrees of freedom

So far we’ve looked at the degrees of freedom for a 3×3 contingency table,

but how do we generalize the result?

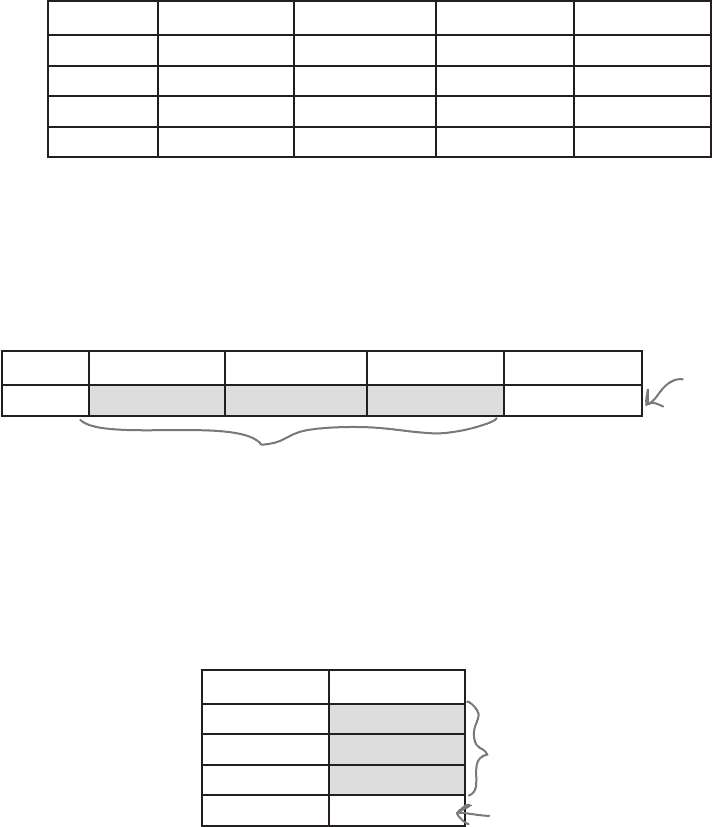
Imagine you’re comparing two variables, and you have h rows of one variable

and k columns of another. You know what the row and column totals should

be. Now imagine you want to find the number of degrees of freedom.

Column 1 ... Column k-1 Column k

Row 1

...

Row h-1

Row h

For each row, there are k columns. You know what the total of each row

should be, so you only actually need to calculate the expected frequency of

(k – 1) of the columns. You automatically know what the kth column is

because you know the total frequency of the row.

Column 1 ... Column k-1 Column k

Row 1

You need to calculate these.

You can figure

out column k using

the row total.

It’s a similar process for the columns. Each column has h rows, and you

know what the total of each column should be. This means that you have

to calculate (h – 1) of the rows for each column. You automatically know

what the value of the hth row is because you know the total frequency of the

column.

Column 1

Row 1

...

Row h – 1

Row h

You need to calculate

the frequencies of

these h-1 rows.

You can figure out row h

using the column total.

calculating degrees of freedom in general

you are here 4 597

the χ

distribution

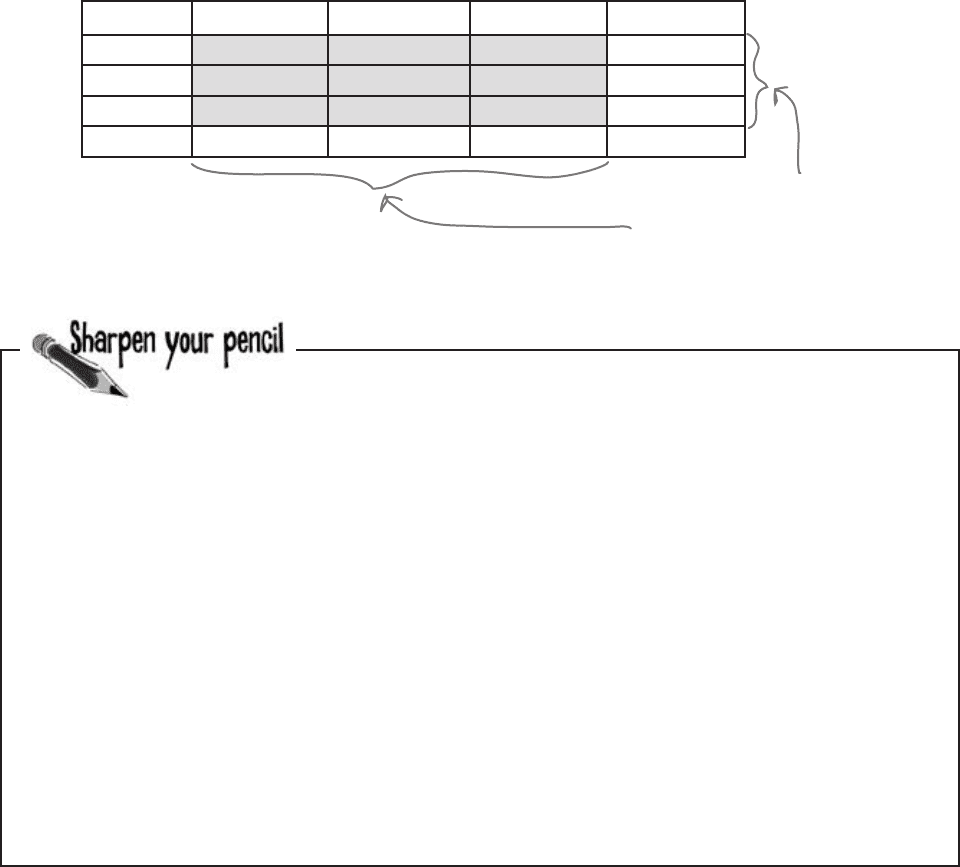
Column 1 ... Column k-1 Column k

Row 1

...

Row h-1

Row h

ν = (h - 1)

(k - 1)

And the formula is...

If we put this together, the total number of expected frequencies

you have to calculate is (k - 1)

(h - 1). In other words, if you have a

table with dimensions h by k, you can find the degrees of freedom by

calculating

You have to calculate (h-1) x (k-1)

expected frequencies, so there are

(h-1) x (k-1) degrees of freedom.

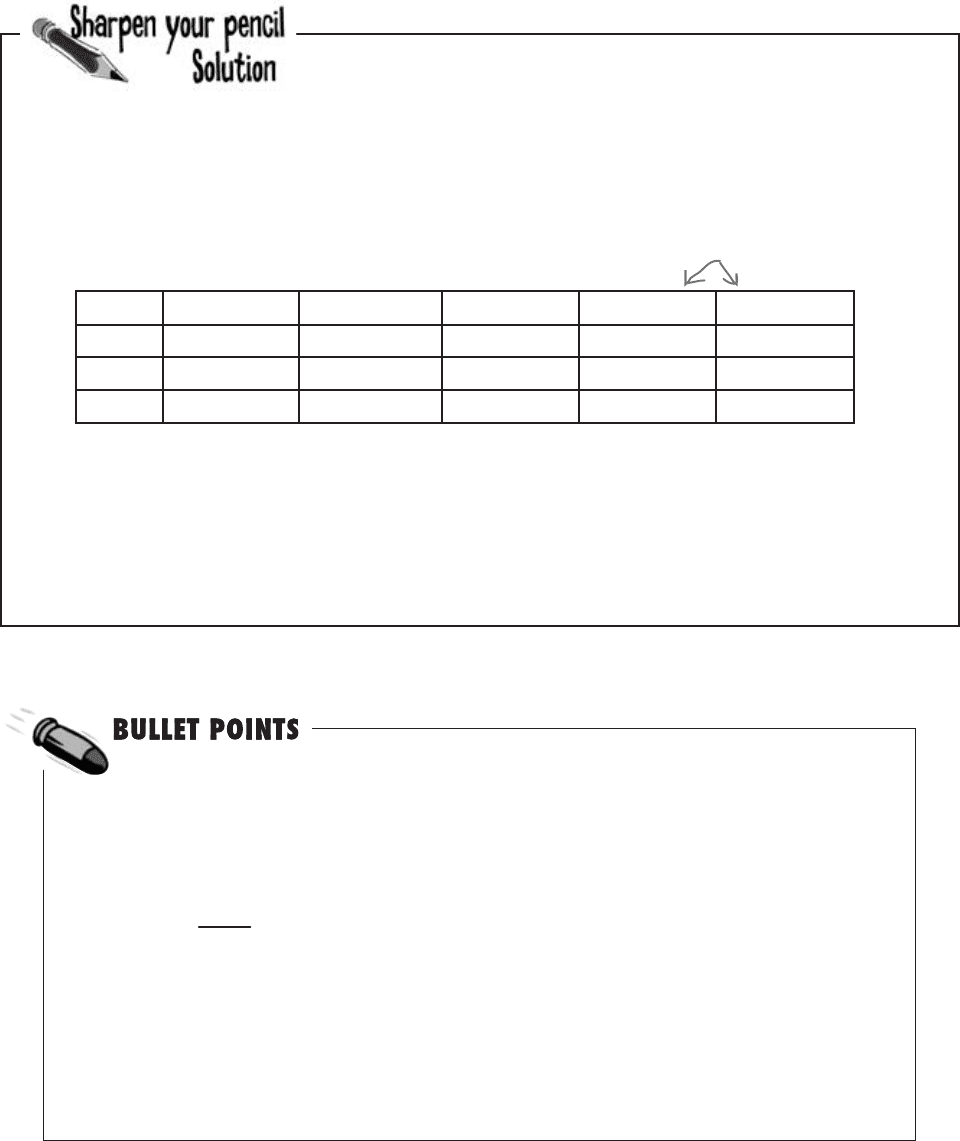
Fat Dan has hired two more croupiers. What are the degrees of

freedom now? The outcomes of the game remain the same.

598 Chapter 14

Fat Dan has hired two more croupiers. What are the degrees of

freedom now? The outcomes of the game remain the same.

As Fat Dan has hired 2 more croupiers, this means that we now have a 3x5 contingency table.

Croupier A Croupier B Croupier C Croupier D Croupier E

Win

Draw

Lose

A, B, and C are the original croupiers,

and Fat Dan has hired two more.

The number of degrees of freedom is given by (h-1) x (k-1), where h is the number of rows, and k is the number

of columns. This gives us

ν = 2 x 4

= 8

The χ

distribution allows you to conduct goodness

of fit tests and test independence between

variables.

It takes a test statistic

(O - E)

where O refers to observed frequencies, and E

refers to expected frequencies.



If we’re using test statistic Χ

with the χ

distribution, we write

~ χ

(ν)

where ν is the number of degrees of freedom, and

α is the level of significance.

In a goodness of fit test, ν is the number of

classes minus the number of restrictions.

In a test for independence for two variables, if your

contingency table has h rows and k columns,

ν = (h – 1)

(k – 1)



sharpen solution

you are here 4 599

the χ

distribution

You’ve saved the casino

Thanks to your mastery of the χ

distribution, you’ve managed to

unearth which of the casino games look like they’ve been rigged. You

discerned explainable discrepancies between what you got and what you

expected, and you also detected suspicious activity at certain levels of

significance.

Fat Dan is delighted with your efforts. Thanks to you, he knows which of

his casino games need to be investigated, and the blackjack croupiers get

to keep their jobs. Next time you’re in town, tell Fat Dan—he’ll supply

you with extra chips, all on the house.

Well done!

Fat Dan’s promised you

a bunch of casino chips

on the house!

600 Chapter 14

Fat Dan thinks that one or more of his croupiers are somehow influencing the results of the roulette

wheel. Here’s data showing the observed frequency with which the ball lands in each color pocket

for each of the croupiers. Conduct a test at the 5% level to see whether pocket color and croupier

are independent, or whether there is sufficient evidence to show there might be something going on.

Step 1: Decide on the hypothesis you’re going to test, and its alternative.

Step 2: Find the expected frequencies and the degrees of freedom. Use the table of expected frequencies below.

Step 3: Determine the critical region for your decision.

Croupier A Croupier B Croupier C

Red

375 367 357

Black

379 336 362

Green

46 37 41

Croupier A Croupier B Croupier C Total

Red

1099

800/2300=382.3 1099

740/2300=353.6

Black

1077

800/2300=374.6

Green

124

800/2300=43.1

Total

800

Hint: Complete the row and column totals first these are

the same as for the observed frequencies above.

chapter-ending long exercise