Griffiths D. Head First Statistics

Подождите немного. Документ загружается.

you are here 4 631

correlation and regression

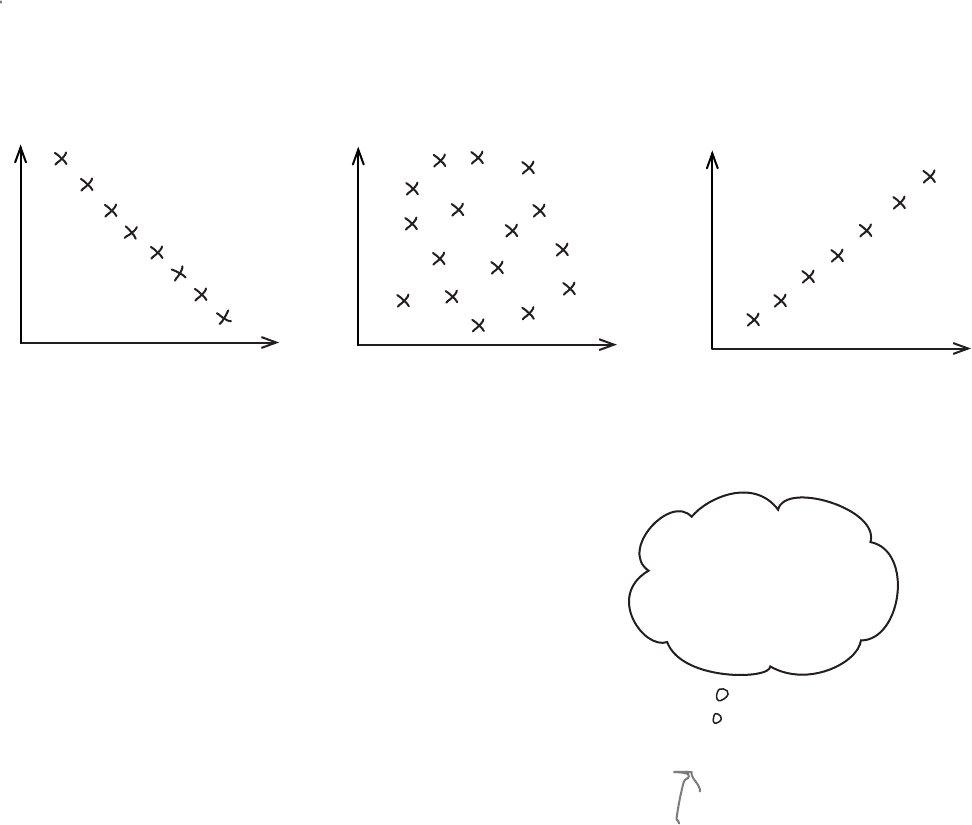
The correlation coefficient is a number between -1 and 1 that describes the

scatter of data points away from the line of best fit. It’s a way of gauging how

well the regression line fits the data. It’s normally represented by the letter r.

If r is -1, the data is a perfect negative linear correlation, with all of the

data point in a straight line. If r is 1, the data is a perfect positive linear

correlation. If r is 0, then there is no correlation.

r=-1

r=0

r=1

Usually r is somewhere between these values, as -1, 0, and 1

are all extreme.

If r is negative, then there’s a negative linear correlation

between the two variables. The closer r gets to -1, the stronger

the correlation, and the closer the points are to the line.

If r is positive, then there’s a positive linear correlation

between the variables. The closer r gets to 1, the stronger the

correlation.

In general, as r gets closer to 0, the linear correlation gets

weaker. This means that the regression line won’t be able to

predict y values as accurately as when r is close to 1 or -1. The

pattern might be random, or the relationship between the

variables might not be linear.

If we can calculate r for the concert data, we’ll have an idea

of how accurately we can predict concert attendance based

on the predicted hours of sunshine. So how do we calculate r?

Turn the page and we’ll show you how.

I’m the correlation

coefficient, r. I

say how strong the

correlation is between

the two variables.

Think of r as standing

for relationship.

The correlation coefficient measures how well the line fits the data

632 Chapter 15

So how do we calculate the correlation coefficient, r?

We’re not going to show you the proof for this, but the correlation

coefficient r is given by

where s

is the standard deviation of the x values in the sample, and s

the standard deviation of the y values.

I get it. We use

the value of b to

help us calculate r.

r = b s

We’ve already done most of the hard work.

Since we’ve already calculated b, all we have left to find is s

and s

. What’s

more, we’re already most of the way towards finding s

When we calculated b, we needed to find the value of Σ(x - x)

. If we divide

this by n - 1, this actually gives us the sample variance of the x values. If we

then take the square root, we’ll have s

. In other words,

is the standard deviation of the x values in the

sample. s

is the standard deviation of the y values.

b is the slope of the line

of best fit that you’ve

already found.

This is the

standard deviation

of the x values in

the sample, it’s the

same formula you’ve

seen before

You calculated this bit

earlier, so there’s no need

to calculate it again.

The only remaining piece of the equation we have to find is s

, the standard

deviation of the y values in the sample. We calculate this in a similar way to

finding s

Let’s try finding what r is for the concert attendance data.

This is the standard deviation of the x values in the

sample, and you’ve done these sorts of calculations before.

calculating the correlation coefficient

There’s a formula for calculating the correlation coefficient, r

√

Σ(x - x)

n - 1

√

Σ(y - y)

n - 1

you are here 4 633

correlation and regression

Find r for the concert data

Let’s use the formula to find the value of r for the concert data. First of

all, here’s a reminder of the data:

x (sunshine)

1.9 2.5 3.2 3.8 4.7 5.5 5.9 7.2

y (attendance)

22 33 30 42 38 49 42 55

To find r, we need to know the values of b, s

, and s

so that we can use

them in the formula on the opposite page. So far we’ve found that

b = 5.32

but what about s

and s

Let’s start with s

. We found earlier that Σ(x - x)

= 23.02, and we know

that the sample size is 8. This means that if we divide 23.02 by 7, we’ll

have the sample variance of x. To find s

, we take the square root.

Σ(y - y)

= (22 - 38.875)

+ (33 - 38.875)

+(30 - 38.875)

+(42 - 38.875)

+ (38 - 38.875)

(49 - 38.875)

+ (42 - 38.875)

+ (55 - 38.875)

= (-16.875)

+ (-5.875)

+ (-8.875)

+ (3.125)

+ (-0.875)

+ (10.125)

+ (3.125)

+ (16.125)

= 780.875 (to 2 decimal places)

The only piece of the formula we have left to find is s

. We already know

that y = 38.875, as we found it earlier on, so this means that

We can now use this to find s

, by dividing by n - 1 and taking the square

root.

All we need to do now is use b, s

, and s

to find the value of the

correlation coefficient r.

This is the slope of the line we found earlier.

This is the standard deviation of the x values. It’s a sample,

so we divide by n - 1.

Finally, we use the y values in the sample

to find s

, the standard deviation of y.

= (23.02/7)

= 3.28857

= 1.81 (to 2 decimal places)

= (780.875/7)

= 111.55357

= 10.56 (to 2 decimal places)

634 Chapter 15

I’ve seen other ways of calculating

r. Are they wrong?

A: There are several different forms of the

equation for finding r, but underneath, they’re

basically the same. We’ve used the simplest

form of the equation so that it’s easier to

see what you’ve already calculated through

finding b.

Are the results accurate with such

a small sample?

A: A larger sample would definitely be

better, but we used a small sample just to

make the calculations easier to follow.

You haven’t proved or derived why

you calculate the values of b and r in this

way. Why not?

A: Deriving the formula for b and r is quite

complex and involved, so we’ve decided not

to go through this in the book. The key thing

is that you understand when and how to use

them.

What’s the expected concert

attendance if the predicted hours of

sunshine is 0?

A: We can’t say for certain because this

is quite a way outside the range of data we

have. The line of best fit is a pretty good

estimate for the range of data that we have,

but we can’t say with any certainty what

the concert attendance will be like outside

this range. The data might follow a different

pattern outside this range, so any estimate

we gave would be unreliable.

When we were looking at averages,

we saw that univariate data can have

outliers. What about bivariate data?

A: Yes, bivariate data can have outliers

too. Outliers are points that lie a long way

from your regression line. If you have

outliers, then this can mean that you have

anomalies in your data set, or alternatively,

that your regression line isn’t a good fit of

the data.

I’ve heard of influential

observations. What are they?

A: Influential observations are points that

lie a long way horizontally from the rest of

the data. Because of this, they have the

effect of pulling the regression line towards

them.

So is an influential observation the

same as an outlier?

A: No. Outliers lie a long way from the

line. Influential observations lie a long way

horizontally from the data.

Find r for the concert data, continued

r = bs

= 5.32 x 1.81/10.56

= 0.91 (to 2 decimal places)

As r is very close to 1, this means that there’s strong positive

correlation between open air concert attendance and hours

of predicted sunshine. In other words, based on the data that

we have, we can expect the line of best fit, y = 15.80 + 5.32x,

to give a reasonably good estimate of the expected concert

attendance based on the predicted hours of sunshine.

sunshine (hours)

attendance (100’s)

0 1 2 3 4 5 6 7 8

r = 0.91

calculating r and no dumb questions

Now that we’ve found that b = 5.32, s

= 1.81, and s

= 10.56,

we can put them together to find r.

you are here 4 635

sunshine (hours)

attendance (100’s)

0 1 2 3 4 5 6 7 8

r = 0.91

Awesome, dude, you rock!

Here’s a free ticket for

our next event.

You’ve saved the day!

The concert organizers are amazed at the work you’ve done with

their concert data. They now have a way of predicting what

attendance will be like at their concerts based on the weather

reports, which means they have a way of maximizing their profits.

Woah dude! This

regression thang

is boogalicious!

correlation and regression

636 Chapter 15

The evil Swindler has been collecting data on the effect radiation exposure has on Captain

Amazing’s super powers. Here is the number of minutes of exposure to radiation, paired with

the number of tons Captain Amazing is able to lift:

Radiation exposure (minutes)

3 3.5 4 4.5 5 5.5 6 6.5 7

Weight (tons)

14 14 12 10 8 9.5 8 9 6

Your job is to use least squares regression to find the line of best fit, and then find the correlation coefficient to

describe the strength of the relationship between your line and the data. Sketch the scatter diagram too.

If Swindler exposes Captain Amazing to radiation for 5 minutes, what weight do you expect Captain Amazing to be

able to lift?

long exercise

you are here 4 637

correlation and regression

We’ve left you

plenty of space for

your calculations

638 Chapter 15

The evil Swindler has been collecting data on the effect radiation exposure has on Captain

Amazing’s super powers. Here is the number of minutes of exposure to radiation, paired with

the number of tons Captain Amazing is able to lift:

Radiation exposure (minutes)

4 4.5 5 5.5 6 6.5 7

Weight (tons)

12 10 8 9.5 8 9 6

Your job is to use least squares regression to find the line of best fit, and then find the correlation coefficient to

describe the strength of the relationship between your line and the data. Sketch the scatter diagram too.

If Swindler exposes Captain Amazing to radiation for 5 minutes, what weight do you expect Captain Amazing to be

able to lift?

Let’s use x to represent minutes of radiation exposure and y to represent weight in tons. We need to find the

regression line y = a + bx, so let’s start by calculating x and y.

x = (4 + 4.5 + 5 + 5.5 + 6 + 6.5 + 7)/7

= 38.5/7

= 5.5

y = (12 + 10 + 8 + 9.5 + 8 + 9 + 6)/7

= 62.5/7

= 8.9 (to 2 decima

l places)

Next, let’s calculate Σ(x - x)(y - y) and Σ(x - x)

, and then b.

Σ(x - x)(y - y) = (4-5.5)(12-8.9) + (4.5-5.5)(10-8.9) + (5-5.5)(8-8.9) + (5.5-5.5)(9.5-8.9) +

(6-5.5)(8-8.9) + (6.5-5.5)(9-8.9) + (7-5.5)(6-8.9)

= (-1.5)(3.1) + (-1)(1.1) + (-0.5)(-0.9) + (0)(0.6) + (0.5)(-0.9) + (1)(0.1) + (1.5)(-2.9)

= -4.65 - 1.1 + 0.45 + 0 - 0.45 + 0.1 - 4.35

= -10

Σ(x - x)

= (4-5.5)

+ (4.5-5.5)

+ (5-5.5)

+ (5.5-5.5)

+ (6-5.5)

+ (6.5-5.5)

+ (7-5.5)

= (-1.5)

+ (-1)

+ (-0.5)

+ 0

+ 0.5

+ 1

+ 1.5

= 2.25 + 1 + 0.25 + 0 + 0.25 + 1 + 2.25

= 7

b =

Σ(x - x)(y - y)

(x - x)

= -10/7

= -1.43 (to 2 decimal places)

long exercise solution

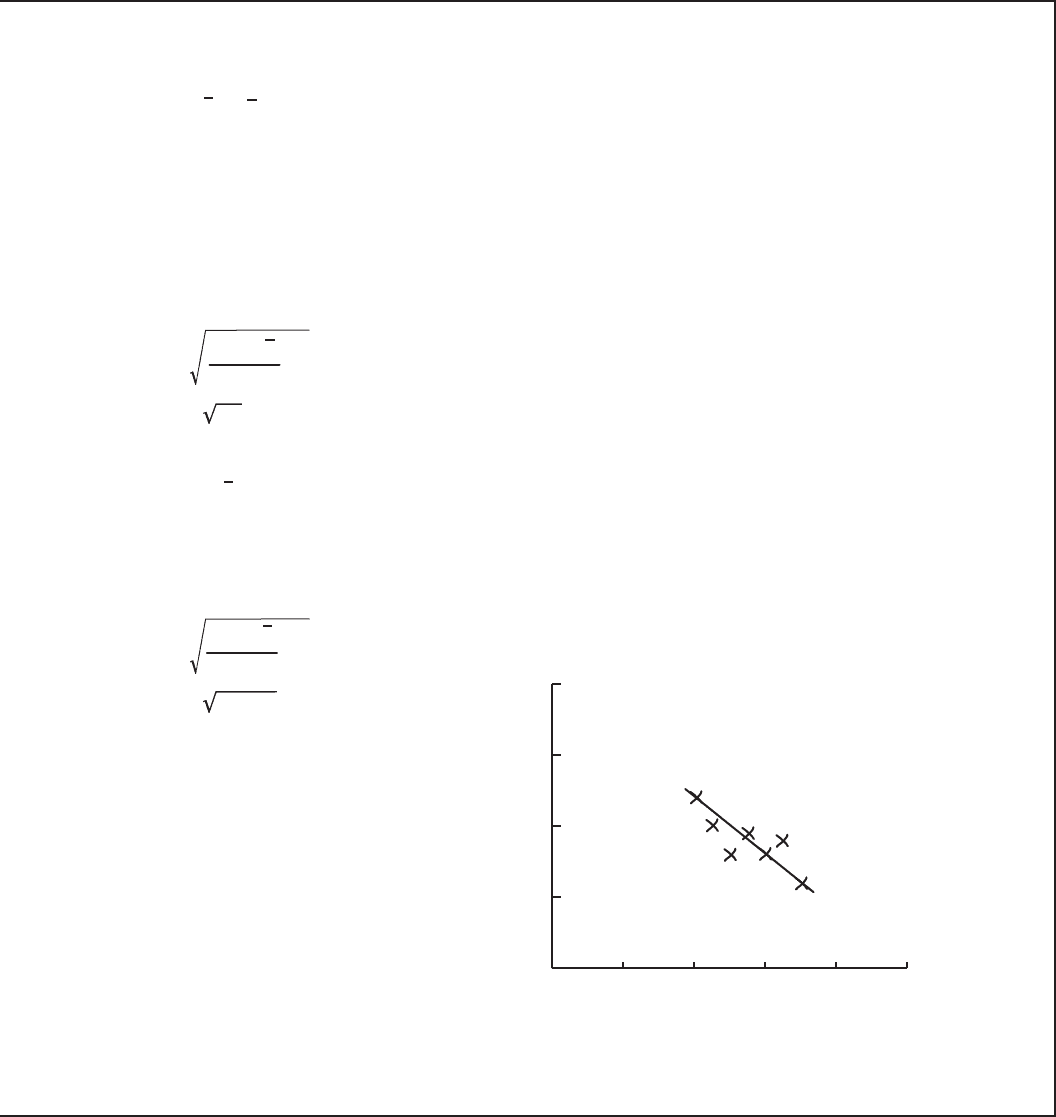
you are here 4 639

correlation and regression

Now that we've found b, let's use it to find a.

a = y - bx

= 8.9 + 1.43 x 5.5

= 8.9 + 7.86

= 16.76

This means that the line of best fit is given by y = 16.76 -1.43x

The correlation coefficient, r, is given by r = bs

where s

and s

are the standard deviations of the x and y

variables. We’ve found b, so we need to find s

and s

= Σ(x - x)

n - 1

= 7/6

= 1.08

Σ(y - y)

= (12-8.9)

+ (10-8.9)

+ (8-8.9)

+ (9.5-8.9)

+ (8-8.9)

+ (9-8.9)

+ (6-8.9)

= 3.1

+ 1.1

+ (-0.9)

+ 0.6

+ (-0.9)

+ 0.1

+ (-2.9)

= 9.61 + 1.21 + 0.81 + 0.36 + 0.81 + 0.01 + 8.41

= 21.22

= Σ(y - y)

n - 1

= 21.77/6

= 1.90

Putting this together gives us

r = bs

= -1.43 x 1.08/1.9

= -0.81 (to 2 decimal places)

If x = 5, then we find y by calculating

y = 16.76 - 1.43x

= 16.76 - 1.43 x 5

= 9.61

In other w

ords, after 5 minutes of exposure to radiation, we'd expect Captain Amazing to be able lift 9.61 tons.

Radiation exposure (minutes)

Weight (tons)

y = 16.76 - 1.43x

r = -0.81

108642

640 Chapter 15

Univariate data deals with just one

variable. Bivariate data deals with two

variables.

A scatter diagram shows you patterns in

bivariate data.

Correlations are mathematical

relationships between variables. It does

not mean that one variable causes the

other. A linear correlation is one that

follows a straight line.

Positive linear correlation is when low

x values correspond to low y values,

and high x values correspond to high

y values. Negative linear correlation is

when low x values correspond to high

y values, and high x values correspond

to low y values. If the values of x and y

form a random pattern, then there’s no

correlation.

The line that best fits the data points is

called the line of best fit.

Linear regression is a mathematical way

of finding the line of best fit, y = a + bx.



The sum of squared errors, or SSE, is

given by Σ(y - y)

The slope of the line y = a + bx is

b = Σ(x - x)(y - y)

Σ(x - x)

The value of a is given by

a = y - bx

The correlation coefficient, r, is a number

between -1 and 1 that describes the

scatter of data away from the line of

best fit. If r = -1, there is perfect negative

linear correlation. If r = 1, there is perfect

positive linear correlation. If r = 0, there

is no correlation. You find r by calculating

r = b s



bullet points