Хейденрайх Р. Основы просвечивающей электронной микроскопии
Подождите немного. Документ загружается.


ГЛАВА
8
Интенсивность
дифракции
Изучению
интенсивностей
электронной
дифракции
в
настоя
щее
время
посвящено
большое
число
исследований.
Теоретиче
ский
анализ
все
более
и
более
усложняется
по
мере
того,
как
приходится
переходить
к
приближениям
более
высокого
порядка.
Особенно
это
относится
к
способам
расшифровки
кристалличе
ских
структур
по
данным
электронографии.
Мы
не
можем
пока
что
интерпретировать
распределение
интенсивностей
дифраги
рованных
электронов
так
же
просто,
как
это
удается
в
случае
рентгеновских
лучей.
Поскольку
амплитуды
рассеяния
элек
тронов
значительно
превышают
амплитуды
рассеяния
рентгенов
ских
лучей,
в
процессах
рассеяния
начинают
играть
существен
ную
роль
многократные
отражения.
Учет
же
многократных
отра
жений
связан
с
серьезными
трудностями,
которые
могут
быть
преодолены
только
на
основе
динамической
теории,
да
и
то
лишь
путем
аппроксимаций.
К
усложнениям
приводит
инеупругое
рассеяние,
избавиться
от
которого
в
эксперименте
значительно
труднее,
чем
от
некuгерентной
части
дифрагированного
рентге
новского
излучения.
Качественно
зависимость
интенсивности
дифракции
электронов
от
различных
физических
факторов
не
очень
трудно
себе
представить,
но
при
попытках
количественного
анализа
мы
сразу
же
оказываемся
в
сложнейшем
лабиринте.
Анализ
рассеяния
электронов
в
рамках
волновой
механики
основан
на
использовании
уравнения
Шредингера
(5.2б)
V
2
1p
+
8~:m
[Е
- V
(х,
у,
z)]
1р
=
О,
которое
часто
записывают
в
виде
(8.1)
где
Н
-
оператор
Гамильтона:
- [ h
2
2 V )-,
.Н
=
--8
2 V +
(х,
у,
z J
лm
,
гл.
8.
ИНТЕНСИВНОСТЬ
ДИФРАНЦИИ
243
Как
и
в
предыдущей
главе,
электростатичеСRИЙ
ПО'fенциа~
в
Rристалле
представляется
в
виде
разложения
в
трехмерныи
ряд
Фурье:
V
(х,
у,
z)
= -
е
[ио
+
~'
Vgе21щgг)]
g
(8.2а)
с
коэффициентами
Фурье
Vg
= (1/300) V
hkZ
,
определяемыми
урав
нением
(7.8а)
V
-
48
~
f.
(s)
е
2лi
(hu+hv+lw)
hkl--
Q
~
J •
(8.2б)
j
Во
многих
случаях
ряды
(7.6в)
медленно
сходятся,
и
поэтому
при
расшифровке
реальных
структур
приходится
учитывать
боль-·
шое
количество
членов
ряда.
Прежде
чем
переходить
R
подробному
иизложению
расчетоВ'
интенсивностей
дифракции,
наметим
общии
подход к
решени~
уравнения
(8.1).
В
случае
быстрых
электронов
и
С
энергиеи
Е
2>
V
(х,
у,
z)
применимы
методы
теории
возмущении,
или
после~
довательных
приближений.
В
принципе
эти
MeTOД~
довольно
просты
и
находят
широкое
применение
в
KBaHTOBO~
механике
(1.2).
Но
вычисление
членов
ряда
теории
возмущении
во
втором
и
более
высоких порядках
связано
с
про
ведением
длинных
и
гро
моздких
расчетов.
Поэтому
в
задачах,
требующих
проведения
таких
расчетов,
вообще
говоря,
лучше
пользоваться
числ~нными
методами.
Теория
возмущений
основывается
на
предположении
о
том,
что
возмущающий
потенциал
достаточно
мал,
так
что
решения
близки
к
решениям,
справедливым
в
его
отсутствие.
Есили
потен
циал
в
(5.2б)
или
(8.1)
положить
равным
нулю
(или
другои
постоян
ной
величине),
то
решения
будут
соответствовать
нулевому
при
ближению.
Уравнение
(8.1)
тогда
записывается
в
виде
f)l,B
Н(О)=
(-~V2-evo)
.
8л
2
m
(8.За)
Это
уравнение
имеет
решение,
найденное
в
гл.
5
(5.9б)
и
описы
ваемое
плоской
волной
цк
.г)
(8
Зб)
Uj
= const
е
J.
•
Можно
ПОRазать,
что
решение
волнового
уравнения
(8.1)
с
потенциалом,
отличным
от
нуля,
имеет
вид
разлошения
в
ряд
по
известным
решениям
нулевого
приближения
1р
=
~
CjUj,
(8.Зв)
j
16*

244
ГЛ.
8.
ИНТЕНСИВНОСТЬ
ДИФРАНЦИИ
где
коэффициенты
C
j
должны
БPIТЬ
определены
1).
:Когда
потен
циал
является
периодическим,
решение
(8.Зв)
есть
функция
Блоха
(см.
[З
1),
или
плоская
волна,
Модулированная
с
периодом,
равным
периоду
потенциала.
Если
(8.Зв)
и
(8.2а)
подставить
в
уравнение
Шредингера,
то
~олучим
2)
(8.Зг)
где
EjO)
=
h21
к
зО)
I 2
/8л
2т
-
кинети~еская
энергия,
связанная
с
волновым
вектором
KjO).
Если
(8.Зг)
умножить
на
комплексно
сопряженную
функцию
иiп
и
затем
проинтегрировать
по
объему
системы,
то
в
результате
получим
~
Е
~
u~!V
(х,
у,
z)
Uj
dQ +
(E
j
-Е)"
~
U~llj
dQ
] C
j
=
О.
(8.Зд)
j Q Q
Поскольку
функции
Uj
ортогональны
3),
уравнения
(8.Зд)
можно
свести
к
бесконечной
системе
уравнений
(8.4а)
(Заряд
электрона
е
здесь
включен
в
потенциалы.)
Эта
система
представляет
собой
«уравнение
дисперсию>
4),
полученное
Бете
{4]
в его
оригинальной
статье,
в
.которой
развивается
динамиче-
,ская
теория
дифрю{ции
электронов.
Уравнения
(8.4а)
представ
ляют·
собой.
общие
соотношения
между
амплитудами,
коэффи
циентами
Фурье
потенциала
и
полной
энергией
электрона
Е.
:Эти
уравнения
могут
быть
записаны
и
через
коэффициенты
Фурье
и
g,
определяемые
равенством
8л
2
m
U
g
=~eVg.
Здесь
8л
2
m/
h
2
выр~жается
в
эв
Х
А
2,
или
(э.
с.
е.
А
2)
-1,
так
что
и
g
выражается
в
А -
2.
Уравнение
Шред~нгера
не
может
быть
решено
в
общем
слу
чае.
В
связи
с
этим
нами
будут
получены
приближенные
решения.
За
нулевое
приближение
примем
результат,
получающийся
при
1)
Это
выражение
представляет
собой
не
зависящую
от
времени
часть
(4.4).
2)
В
выражении
(8.Зг)
по:генциал
кристалла
Vo
включен
в
Е.
\'
и
.и*
dQ=
{О
при
j
4=-
т,
3)
J J
т
1
при
j =
m.
Q
4)
У
равнением
дисперсии
обычно
называется
уравнение,
которым
опре
деляется
спектр
энергии.
В
данном
случае
уравнением
дисперсии
является
равенство,
получаемое
приравниванием
нулю
определителя
системы
(8.4а).
ПРUJtt.
перев.
всех
Vj
=
О:
или
ГЛ.
8.
ИНТЕНСИВНОсТЬ
ДИФРАНЦИИ
h21
K~
12
Е+ио=
8л
2
m
245
(8.4б)
(см.
гл.
5).
Если
пренебречь
граничными
условиями,
то
нулевое
приближение
представляет
собой
кинематическую,
или
геомет
рическую,
теорию
дифракции,
которая
излагается.
в
§ 1.
Следует
отметить
что
если
в
волновую
функцию
нулевого
приближения
ввести
a'd
/юс
волновой
вектор
дифрагированной
волны
K
g
.
=
=
Ко
+
2лg, то
получим
'Ф
=
Coei(Kr)
+
С
gei(Kgf).
(8.5)
Но
в
силу
граничных
условий
(5.11а)
на
поверхности,
через
кото
рую
в
кристалл
проникает
излучение,
придется
положит!>
C
g
=
О,
поскольку
амплитуда
дифрагированнои
волны
на
этои
поверх
ности
должна
равняться
нулю.
В
результате
у
нас
не
будет
ника~
кого
дифрагированного
пучка.
Чтобы
решен~е
допускало
суще
ствование
дифрагированной
волны
с
отличнои
от
нуля
амплиту:
дой,
нужно
ввести
еще
одну
волну,
интерфuеренция
с
которои
привела
бы
к
нулевой
амплитуде
на
внешнеи
поверхности
кри
сталла.
Если
в
кристалле
существует
одна
дифрагированная
волна,
то
она
должна
иметь
вид
C
g
(1-
еilДКlz)
ei(Kgf>,
и
тогда
ее
амплитуда
будет
обращаться
в
нуль
при
z =
о.
Таким
образом,
в
кинематической
теории
сразу
же
нарушаются
гра
ничные
условия,
а
прямая
подстановка
в
уравнение
(5.2б)
пока~
зывает,
что
(8.5)
не
удовлетворяет
этому
уравнению,
если
только
не
выполняется
условие
C
g
=
О.
Решение
в
нулевом
приближении
допускает только
одну
амплитуду
Со.
В
первом
приближении
в
системе
(8.4а),
кроме
СО,
остается
еще
один
коэффициент
Фурье,
например
Vg.
Остав
ляя
в
(8.4а)
амплитуды
с
т
=
~т
= g,
получаем
(Ео--Е)
CO-v;С
g
=
О,
-vgС
О
+
(E
g
-Е)
C
g
=
О,
где
V_g
= Vg.
Систему
(8.6а)
удобно
записать
в
виде
(
Ео-Е)
-V
g
)
(СО)_О
-Vg
(Eg-E)
C
g
- .
(8.ба)
Она
имеет
нетрив:иальное
решение
только
в
том
случае,
если
ее
детерминант
равен
нулю.
Энергия
электрона
Е
тогда
дается

246
ГЛ.
8.
ИНТЕНСИВНОСТЬ
ДИФРАRЦИИ
выражением,
принимающим
два
значения:
(8.6б)
ЭRсперим~нт
по
дифракции
проводится
при
ПОстоянном
зна
чении
ПОЛНОИ
энергии
электрона
Е.
Поэтому
уравнением
(8.6б)
определяются
дозволенные
состояния
1\инетической
энергии
или
волновые
векторы
волн
в
кристалле,
которые
удовлетворяю;
гра
ничным
условиям.
Единственный
случай,
в
1\ОТОРОМ
ВОЗможно
ТОчное
решение
(исключая определенные
частные
случаи)
_
это
как
раз
и
есть
случай
двух
волн.
Удивительно
то,
что
д~ухвол
новое
решение
может
удовлетворительно
описывать
разнообраз
ные
данные
ЭI\сперим~нта
даже
тогда,
1\огда
в
дифракционной
картине
имеется
целыи
ряд
сильных
рефлексов.
Первое
прибли
жение
подробно
рассматривается
в
§ 2.
Расчет
во
втором
приближении
был
выполнен
Бете
для
слу-
чая,
Богда
имеются
две
сильные
волны
т
-
О
и
т
g
а
б
-
=,
также
ела
ые
отражения.
Рефлексы
являются
слабыми
в
том
смысле
Ф
что
условия
Брэгга
или
Лауэ
не
удовлетворяются
точно
и
1\ОЭФ~
ициенты
амплитуд
малы
по
сравнению
с
С
и
С
П
б
о
g.
ри
этом
нео
ходима
малость
коэффициентов
Фурье
по
сравнению
не
с
~,
а,
н~пример,
с
(ЕУ
-
Е),
где
l -
индекс
волны
с
малой
ампл:~
тудом.
Влияние
слабых
волн
учитывается
в
виде
поправки
к
1\ОЭф
фициентам
Фурье
двух
сильных
волн.
Исправленные
потенциалы
называются
динамичеСJli,ими
потен
циалами.
При
использовании
граничных
условий
для
определе
ния
Со
и
C
g
малыми
амплитудами
пренебрегали
и
поэтому
не
приравнивали
их
к
нулю
на
внешней
поверхности
кристалла.
Из-за
этого
упущения
Мияке
[5]
пришел
к
выводу,
что
приближение
второго
порядка
не
Сводится
к
кинематическому
или
нулевому
приближению
при
лt
---7-
о,
где
t -
толщина
~ристалла
Но'
кан УRазал
Гьенн
[6],
это
объясняется
тем,
что
мы
пренеб~егае~
граничными
условиями
и
вследствие
этого
решение
применимо
ТОЛЬRО
R
бесконечному
кристаллу.
В
измененных
Выражениях
попраВRа содержит
мнимую
часть.
Наличие
Мнимой
части
в
дина
мичеС1\ИХ
потенциалах
приво
....
1\
периодичеС1\ОМУ
у.меньшению
Ф
амплитудь:
строгого
двухволнового решения,
что
вряд
ли
имеет
изичеСRИИ
смысл.
Если
дисперсионное
уравнение
(8.4а)
допускает
существова
~ие
трех
сильнь:х
волн
о,
g
и
Л,
то
появляется
четвертая
амплитуда
8'
для
RОТОРОИ
s = g +
л
даже
при
~'B
=
о.
Эта
«запрещеннаю)
аМПлитуда
может
быть
достаточно
сильной,
чтобы
объяснить
появление
сиЛьного
рефлеRса
(222)
при
рассеянии
на
структуре
алмаза
~
[7].
Можно
думать,
что
С
л
возникает
в
результате
дву
кратнои
дифраRЦИИ
волн
g
и
л
[8].
Тан,
например,
если
g = (111)
r
ГЛ.
8.
ИНТЕНСИВНОСТЬ
ДИФРАRЦИИ
247
и
л
= (113),
то
s = (222).
Эти
явления
получили
название
«слу
чайных»
взаимодействий
[9]
в
отличие
от
«систематичеСRИХ»
взаимодействий,
рассмотренных
Хёрни
[10].
Рентгеновский
ана
лог
запрещенных
электронных
рефлексов
был
обнаружен
Рен
нингером
[11]
и
часто
называется
(<эффектом
Реннингерю).
Если
не
считать
определенных
специальных
случаев,
система
уравнений
(8.4а)
при
наличии
трех
или
более
сильных
волн
с
трудом
может
быть
решена
численно.
Для
<т-волнового»
случая
были
использованы
методы
уравнений
в
конечных
разностях,
осно
ванные
на
методе
Дарвина
[12],
т. е.
на
учете
последовательных
отражений
от
ряда
кристаллических
ПЛОСRостеЙ.
Наиболее
ясным
и
наглядным
является
способ
решения,
основанный
на
понятии
матрицы
рассеяния,
предложенный
Стэрки
[13].
ТаRИМ
же
спо
собом
решали
n-волновую
задачу
и
систему
n
уравнений
Хоуи
и
Уэлан
[14],
Фуджимото
[15]
и
Нирс
[16].
Все
эти
методы
имеют
важное
значение
и
представляют
большую
ценность,
но
лишь
иаи
математические
методы.
Они
не
вносят
ничего
нового
в
ту
физическую
Rартину,
которую
можно
себе
представить
на
основе
двух
волнового
приближения.
Поэтому
для
ознакоцления
с
дета
лями
мы
отсылаем
читателя
R
литературе.
Следует,
однако,
заме
тить,
что
в
методах,
основанных
на
той
или
иной
модели
или
механизме
дифракции,
легко
проглядеть
специфические
кванто
вомеханические
свойства
частиц.
Это
особенно
относится
к
тому
случаю,
когда
поглощение
электронов
рассматривается
так
же,
каи
рассеяние
рентгеновских
лучей.
Если
при
этом
не
учиты
вать,
что
взаимодействие
электронов
должно
описываться
куло
повским
потенциалом,
то
можно
прийти
к
неверным
результатам.
Нелокальный
характер
столкновений
(см.
гл.
6, §
2)
является
квантовомеханической
особенностью
рассеяния
электронов
и
при
водит
к
иному
результату,
чем
столкновения
с
фотонами
при
рассеянии
рентгеновских
лучей.
По
этой
причине
нужно
быть
осторожным
при
проведении
широкой
аналогии
между
физиче
ской
оптикой
нейтральных
фотонов
и
поведением
отрицательно
заряженных
электронов.
Если
волновые функции,
полученные
методами
геометрической
оптики,
не
являются
решениями
урав
нения
Шредингера
и
не
удовлетворяют
граничным
условиям,
то
их
правильность
представляется
сомнительной.
Уравнение
Шредингера
(5.2б)
становится
неприменимым
в
реля
тивистской
облас1'И
даже
при
введении
в
него
простой
релятивист
ской
поправки
к
массе
и длине
волны.
Фудживара
1)
получил
релятивистское
обобщение
(5.2б),
которое
представляет
интерес,
IIОСКОЛЬRУ
исследованиям
в
области
мегавольтной
электронной
микроскопии
и
дифракции
уделяется
все
больше
внимания.
Для
1)
См.
[2]
в
гл.
5.

248
гл.
8.
ИНТЕНСИВНОСТЬ
ДИФРАНЦИИ
непосредственного
сравнения
с
(5.2б)
это
уравнение
V2",
+
8л2mо
[h
2
r
k
12
- J
'у
1~2
8л2mо
xVo
Ф
=
о
может
быть
записано
в
виде
8л2mо
L
C
-
mос
2
- - ]
V
2
ф+JГ
-2-(х2-1)--хVО
'$=--0.
(8.7а)
Здесь,
как и
ранее,
х
=
(1
-
у2)
-1/2,
а
VO
-
потенциал
электрона
с
массой
покоя
то.
Сравнение
(8.7а)
и
(5.2б)
показывает,
что
в
динамические
переменные,
которыми
мы
все
время
пользуемся,
следует
вводить
поправки:
Е:;..:::
eV
a
--7Ч2
тос
2
(х
2
-1)
= V
a
(1
+
0,978
.10-
G
V
а
),
(8.7б)
v
g
--->
v<;)x
==
v<;)
(1_
у
2//
2
.
Особый
интерес
представляют
характерные
динамичеСRие
длины,
в
которые
входит
произведение
ЛЕ.
Величина
лЕ
должна
быть
заменена
следующим
образом:
ЛЕ
-7
lj2/zc Vx
2
-1
=
1/
2
hcy
(1-
у2)-1/
2
.
(8.7в)
Тем
самым
выражение
дЛЯ
ЭRСТИНКЦИОННОЙ
длины
при
рассеянии
под
брэгговским
углом
заменяется
в
реш:rтивистсн:ом
случае
на
выражение
лЕ
hc 6,14·103
t
o
= -
~
2ТОТ
V =
(О)
V
ангстрем.
(8.7г)
Vg
v
g
v
g
Для
удобства
численных
расчетов
величины
лЕ
~
л
V
a
(1
+
+
0,978.10-
6
V
a
)
приведены
в
табл.
20
вместе
с
х
=
(1
_
y2)-lj2.
Но
эти
поправки
еще
должны
быть
экспериментально
проверены
при
напряжениях,
превышающих
5 ·104
8.
§ 1.
.кинематическая
теория
дифракции
В
кинематическом,
или
нулевом,
приближении
при
определе
нии
дифрагированных
амплитуд
рассматривается
одна
рассеян
ная
волна,
наблюдаемая
на
большом
расстоянии
от
системы
рас
сеивающих
центров.
Предполагается,
что
падающий
электрон
претерпевает
только
одно
рассеяние,
а
взаимодействие
между
падающей
и
рассеянной
волнами
отсутствует.
Единственным
гра
ничным
условием
является
условие
сохранения
интеНСИВНQСТИ
и
длины
волны.
Сначала
мы
остановимся
на
более
простом
слу
чае,
когда
тепловое
движение
не
принимается
во
внимание.
Случай
плоских
волн
уже
рассматривался
в
гл.
4
при
анализе
дифракции
Фраунгофера.
Вместо
того
чтобы
сразу
же
выписывать
§
1.
НИНЕМАТИЧЕСНАЯ
ТЕОРИЯ
ДИФРАНЦИИ
249
Фиг.
95.
Геометрия
кинематического
рассеяния
на
двух
атомах
1
и
2.-
наХОДЯЩIlХСЯ
на
расстоянии
r12
друг
от
друга.
Прямая
CD
-
след
<ютражающей
плосности»,
I\ОТОРЫЙ
делит
пополам
угол
рассеяния
/3.
Разностями
хода
лучей,
обозначенными
жирными
линиями,
определяется
разность
фаз
волн,
рассеянных
атомами
1
и
2.
Единичные
венторы
So
и
S
параллельны
направле-
ниям
падения
и
рассеяния.
Величины
11
(з)
и
12
(s)
-
амплитуды
рассеяния.
дифракционный
интеграл
(4.18),
мы
сначала
проиллюстрируем
геометрическую
теорию.
Пусть
два
атома
1
и
2
на
фиг.
95
нахо
дятся на
расстоянии
r
1
2.
Пусть
также
11
(s)
и
12
(s)
-
амплитуды
рассеяния.
Если
обозначить
единичный
вектор
в
направлении
падения
через
So,
а
единичный
вектор
в
направлении
рассея
ния
через
S,
то
разность
хода
(разность
отрезков
1 -
А
и
2 -
В)
будет
равной
' '
(8.8а)
Амплитуды
волн,
рассеянные
060ИМИ
атомами,
будут
иметь.
вид
11
ехр
(iKr12S)
и
/2
ехр
( - iKr12S0)'
Полная
амплитуда
волны,
рассеянной
на
угол
~,
на
расстоянии
L
равна
ф
(~)
= 1
(f1eiK(r12S)
+
/2e-iК(f12S0»)
=
Из
фиг.
95
видно,
что
=
--.!.-
e-iКr12Sо
[f1eiK(f12(S-SО»
+ 12]'
L
I
f12
(S
-
So)
1=1
r1211
S -
So
I
Cos
у,
и,
так
нак
\ S -
So
\ = 2
sin
~/2,
разность
хода
равна
2 !
r121
sin
~
cos
у.
(8.86).
(8.8в)

,
250
ГЛ.
8.
ИНТЕНСИВНОСТЬ
ДИФРАНЦИИ
Заметим,
что
разность
фаз
получается
из
раЗНОСТII
хода
умно
жением
на
2л/л,
тю,
что
ИЗ
(8.8в)
для
разности
фаз
имеем
~л
I r121sin
~
coSy=lr
1
2Iscosy,
г~еs==(4л/л)siп(~/2)-параметр
рассеяния,
введенный
в
гл.
1,
§
....
Поскольку
d = I
Г
12
/
СОВ
у,
величина
(8.8в)
может
быть
записана
как
разность
хода
брэгговского
отраrкения
с
максимумами
при
2d
sin
f
n'А
= 2d
sin
~
2 .
(8.8г)
Обратимся
теперь
к
выражению
для
амплитуды
(8.8б).
Под
ставляя
в
него разность
хода
(8.8в),
получаем
интенсивность
I
ф
(~)
/2:=
12
[Л
+
1;
+
2/1/2
cos
(/1'121
s cos
У)1
(8.9а)
с
маRсимумами
при
разности
фаз,
соответствующей
условиям
Брэгга
(8.8г):
I r
1
21
s
cos
у
=
О,
2л,
4л
и
т.
д.
Выражение
(8.9а)
.дает
интенсив~ость
дифрагированной
волны,
рассеянной
на
угол
(3
при
взаимодеиствии
с
двухатомной
молеRулой,
ориентированной
таRИМ
образом,
что
ее
ось
образует
с
направлением
падения
угол
)12
=
(л/2)
+
«(3/2)
-
у.
Ориентация
молеRУЛЫ
учитывается
мно
жителем
сов
у
в
(8.9а).
Если
в
1
с.м,3
имеется
Nслучайным
обра
зом
ориентированных
молеRул,
находящихся
на
случайных
рас
СТОяниях
друг
от
друга
(газ),
то
полная
интенсивность
будет
равна
сумме
интеНСивностей
рассеяния
от
Rаждой
молеRулы.
При
равновероятном
распределении
значений
у
число
молеRУЛ
в
интер
вале
углов
от
у
до
у
+
dy
есть
N /2
sin
у
d)l.
Тогда
интенсивность,
рассеянная
под
углом
~
N
молеRулами,
равна
л
j 1/,
(А)
12
_ N
Г
(/2
12
~
.
. 1
't'
t.J
I
--
2L2 L 1 +
2)
J
юп
у
dy
+
О
л
+
211/2
i
СОВ
(/
Г
1
2)
s cos
у)
sin
у
dy
l =
О
=~
[/2+/2+211
sins[r
1
21
J
L2 1
2,
1 2 s J r
12
I .
(8.9б)
В
Случае
11
=-
12
(двухатомная
молекула
ти:па
С1
2
)
интенсивность
:равна
Iф
(~)
12
= 2
~
/2
[ 1 +
sin
s I r I J
L2 S I r I '
(8.90)
['
I
~
§
1.
НИНЕМАТИЧЕСНАЯ
ТЕОРИЯ
ДИФРАНЦИИ
251
Фиг.
96.
Одномерный
I{ристалл,
состоящий
из
N = n + 1
атомов,
меж
атомное
расстояние
в
I\OTOPOM
равно
а.
Падающая
волна
представляет
собой
плоскую
волну,
характеризуемую
волновым
век
тором
К
и
углом
падения
/3i'
Угол
рассеяния
равен
/3.
Жирными
линиями
обозначена
разность
хода
лучей.
где
I r I -
межатомное
расстояние.
Мы
получили
выражение
(1.
20а),
ноторое
уже
приводили
ранее,
когда
говорил
ось
о
рас
пределении
интенсивности
в
задней
фокальной
плоскости
объеR
тива.
Соотношение
(8.9в)
может
быть
обобщено
на
случай
более
сложных
молеRУЛ
и
использовано
для
интерпретации
дифраR
ЦИИ
на
газах
[17].
В
аморфных
жидкостях
И
твердых
телах,
где
имеется
корреляция
в
расположении
атомов,
последняя
учиты
вается
с
помощью
функции
радиального
распределения
(гл.
1,
§ 2).
Распределение
интенсивности
в
обратной
«решетке»,
соглас
но
(8.9в),
представляет
собой
ряд
диффузных
концентрических
сфер
с
центром
в
начале
координат.
Сфера
отражения
~фера
Эвальда),
проходящая
через
нулевой
узел,
образует
ПОЧТИ
плосt\ое
сечение
обратной
решеТRИ
и
будет
пересеRаться
со
сферами
макси
мумов
интенсивности,
соответствующими
выражению
(8.9).
Если
двухатомные
молеRУЛЫ
с
одинаRОВЫМИ
атомами
полиме
ризуются,
образуя
цепочку
с
межатомным
расстоянием
а,
то
воз
НИRает
линейный
кристалл.
Пусть
в
цеПОЧRе
имеется
N
атомов
и
амплитуда
рассеяния
для
каждого
из
них
равна
t
(8)
(фиг.
96).
Если
первый
атом
находится
в
начале
координат
и
~rl
-
разность
хода
до
l-ro
атома,
то
амплитуда
волны,
рассеянной
на
угол
~,
будет
n
Ф
(~)
=
ei(Kro)
~
t
(s)
e
i
(K6rz).
(8.10а)
l=O
Разность
хода
между
соседними
атомами
выражается
в
виде
б,о
=
а
[sin
(~-
~i)
+
sin
~i],
(8.10б)
252
l'Л.
8.
llНТЕНСИВНОСТЬ
ДИФРАНЦИИ
Учитывая,
что
8rt = l8r
и
используя
тождество
(1.8б)
(приложе
ние
1),
получаем
для
амплитуды
выражение
'ф
(~)
= f (8)
ei(Kro)
'"
ei(Кll\r)
= f (8)
ei(Kro)
ехр
ик
(n
~
1)
6r]
-1
=
~
ехр
(~K6r)
1=0
= f
()
i(Kro)
sin
(К/2)
(n
+
1)
6r
iK(n/2)Or
8
е
sin
(Kj2)
6r
е
.
(8.10в)
(Число
атомов
в
цепи
N = n + 1.)
Тогда
интенсивность
равна
I
'ф
(~)
12
= /2
Si~2
(Kj2)N6r
•
(8.10г)
sш
2
(Kj2)
6r
Выражение
(8.10г)
представляет
собой
интерференционную
функ
цию,
хорошо
известную
в
кинематической
теории
рассеяния.
Распределение
интенсивности
имеет
главные
максимумы,
равные
j2N2,
при
бг
=
hл
(где
h -
целое
число).
:Минимумы
имеют
место
при
бг
= [h +
(1/N)]
л.
Между
главными
максимумами
распо
лагаются
побочные
(см.
табл.
14).
Для
малых
углов
~
и
~i
раз
ность
хода
бг
~
a~.
В
этом
случае
главные
максимумы
и
минимумы
возникают
при
~MaHC
~
л:'
~мин
~
(/~
±
-}
):
(h
=-
О,
1, 2, 3,
...
).
(8.10д)
Половина
ширины
главных
максимумов,
измеренной
в
угловом
интервале,
в
конечных
точках
которого
интенсивность
равна
нулю
1),
даетея
формулой
(8.10е)
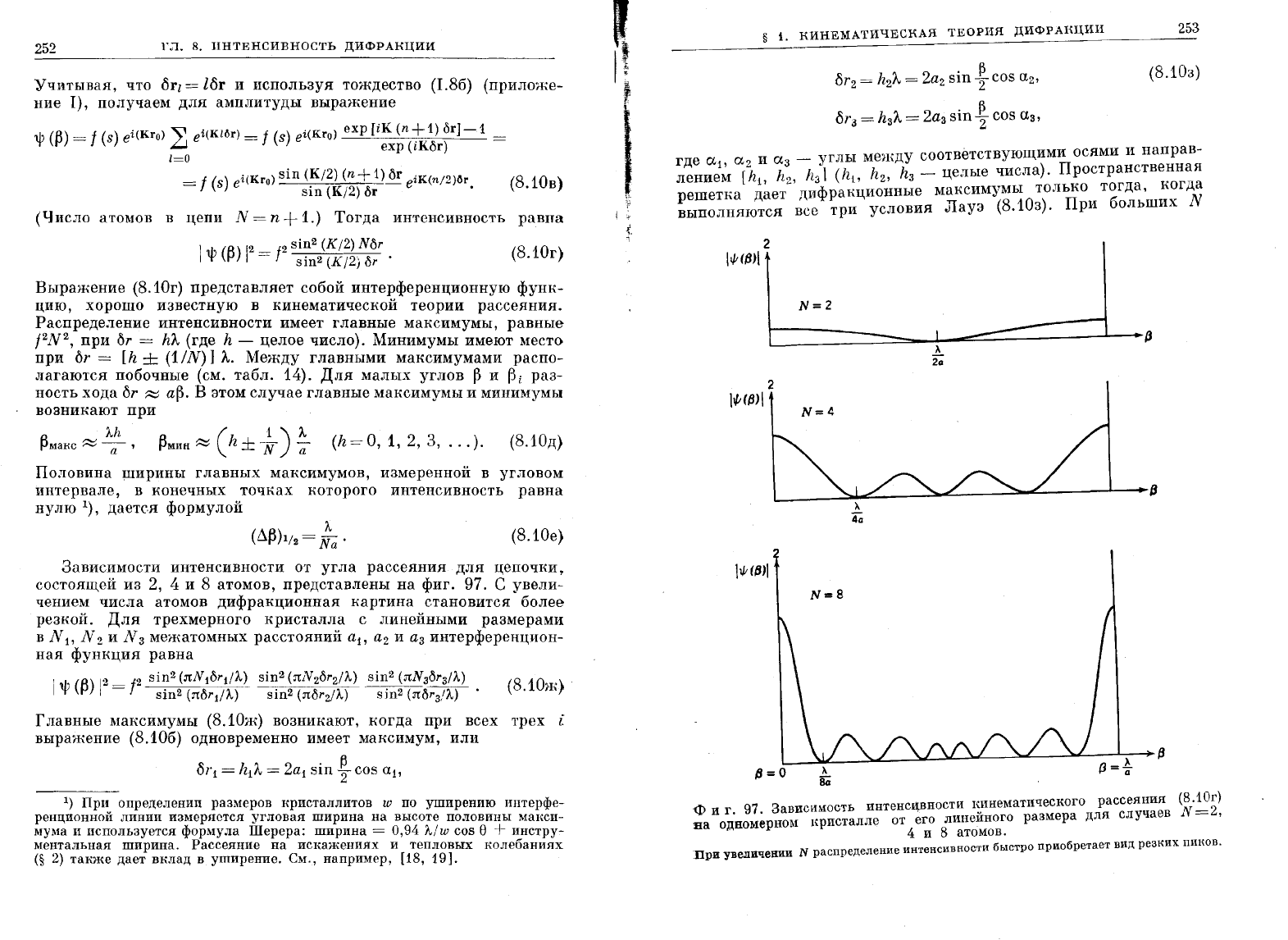
Зависимости
интенсивности
от
угла
рассеяния
для
цепочки,
состоящей
из
2, 4
и
8
атомов,
представлены
на
фиг.
97.
С
увели
чением
числа
атомов
дифракционная
картина
становится более
резкой.
Для
трехмерного
кристалла
с
линейными
размерами
в
N
1,
N 2
И
N
з
межатомных
расстояний
аl,
а2
и
аз
интерференцион
ная
функция
равна
I
'ф
(~)
12
=
f2
sin
2
(лN
I
6Г
l/
Л
)
sin
2
(лN
2
6Г
2/
Л
)
sin
2
(лN
з
6г
зjл)
(8.10ж)
I sin
2
(
л6Г
l/
Л
)
sin
2
(
л6Г
2/
Л
)
sjn
2
(л6
г
з
!л)
.
Главные
максимумы
(8.10ж)
возникают,
когда
при
всех
трех
i
выражение
(8.10б)
одновременно
имеет
маRСИМУМ,
или
81'1
=
1~IЛ
=
2аl
sin
~
cos
аl,
1)
При
определении
размеров
кристаллитов
w
по
уширению
интерфе
ренционной
линии
измеряется
угловая
ширина
на высоте
половины
макси
мума
и
используется
формула
Шерера:
ширина
= 0,94
Л/W
cos
е
+
инстру
ментальная
ширина.
Рассеяние
на
ИСI{ажениях
и
тепловых
колебаниях
(§
2)
также
дает
вклад
в
уширение.
См.,
например,
[18,
19].
I
11.
j
I
I
~
§
1.
НИНЕМАТИЧЕСКАЯ
ТЕОРИЯ
ДИФРАКЦИИ
253
(8.10з)
где
а а
и
а
-
углы
между
соответствующими
осями
и
направ-
1,
[2
h
h
з
I ] (h h h -
целые
числа).
Пространственная
лением
1,
2,
lз
1,
2,
З
решетка
дает
дифракционные
максимумы
только
тогда,
I\Огда
выполняются
все
три
условия
Лауэ
(8.10з).
При
больших
N
2
Iфан\
N=2
>.
га
2
I~(P)\
N=4
N=8
'ф
и
r 97.
ЗависимосТЬ
интенсцвности
I~~нематического
рассеяния
(8.10г)
. -
мера
для
случаев
N
=2,
на
одномерном
I{ристалле
от
его
линеиного
раз
- 4
и
8
атомов.
При
'Увеличении
N
распределение
интенсивноСТИ
быстро
приобретает
вид
реЗl\ИХ
пинов.

254
g
ГЛ.
8.
ИНТЕНСИВНОСТЬ
ДИФРАRЦИИ
Сфера
Эвальда
А
-g
+g
Фиг.
98.
Сфера
Эвальда
в
обратной
pemeTRe
и
ОТRлонение
де
от
Точншо
условия
Брэгга.
Ширина
узла
обратной
решетки
равна
2
(,1/3)1/..
РаССТОяние
BG
ОТ
узла
обратной
решетки
(максимума
интенсивности)
до
сферы
Эвальда
приблизительно
равно
I
<1
I ,1f)
В
литературе
отрезок
BG
часто
обозначают
через
s.
Величина
s
Положительна'"
есл~
IK
1>
I K
g
/.
'
это
требование
оказывается
очень
жестким,
так
как
интерферен
ционная
функция
(8.10ж)
близка
к
дельта-функции
1).
При
ана
лизе
выражения
(8.10ж)
очень
удобно
пользоваться
представле
нием
об
обратной
решетке,
так
как
оно
позволяет
установить
приблиз~тельные
размеры
и
форму
ее
узлов.
Вбл~зи
узлов
обратнои
решетки
Сомножители
выражения
(8.10ж)
могут
быть
записаны
как
N2
sin
2
(лNадВ/л)
[л
(Nа/л)
ДВ]2
,
(8.10и)
где
др
-
угловое
отклонение
от
точного
максимума.
Побочные
максимумы,
возникающие
при
др
= 1,43
(л/а),
2,46
(л/а)
и
т.
д.,
приведены
в
табл.
14.
На
фиг.
98
изображены
узлы
обратной
ре~етки,
лежащие
на
прямой,
и
сфера
Эвальда
для
волны,
падаю
щеи
в
напра~лении
нормали
к
этой
прямой,
причем
показан
угол
др.
Волновои
вектор
К
g
/2л
= AG
не
удовлетворяет
уравнению
1)
Дельта-фУНRЦИЯ
обладает
следующими
свойствами:
+00
6(x-хо)=О
при
x:f=xo
и
~
6(x-
x
o)dx=1.
r
§ 1.
ИИНЕМАТИЧЕСИАЯ
ТЕОРИЯ
ДИФРАRЦИИ
255-
(7.10б)
-
условию
Лауэ
\
К
12
= 1
К
+
2лg
12.
Если
бы
центр
сферы
Эвальда
сместился
из
А
в
А'
при
повороте
около точки
О,
то
условия
дифракции
были
бы
удовлетворены.
Из
чертежа
легко
видеть,
что
отклонение
от
угла
Брэгга
д8
удовлетворяет
соотно
шению
2 (
8::m
)
д
==
1
к
12
--1
K
g
12
= 4 I g I
д8
I
К
1
л
cos
80
~
~
2д8
1
К
12
siп
280'
(8.11а)
так
как
для
быстрых
электронов
cos
80
~
1.
Здесь
80
-
брэг
говский
угол
И
использован
закон
Брэгга
\ g 1 =
(К/л)
sin
80'
Расстояние
GB
в
обратном
пространстве
от
узла
обратной
решетки
до
сферы
Эвальда
равно
I
к
1-1 K
g
I I
к
I
д8
'-
28
-
д8
2л
=~
Ыll
o-g
.
(8.11б).
Ногда
сфера
Эвальда
проходит
через
центр
узла
обратной
решетки
(например,
О),
изменение
интенсивности
дается
выра
жением
(8.10и),
которое
при
w = N
а
и
д6
=
д~
/л
может
быть
записано
в
виде
N
2 1 f ( )
12
sin
2
(лwд~)
s
(ЛWL\s)2
•
(8.11в)
Эта
величина
иногда
называется
кинематичесн.оЙ
трансформантой
формы
в
направлении
6.
Сфера
Эвальда,
так
сказать,
опробует
трансформанту
формы
на
расстоянии
BG
от
максимума.
Для
прямоугольного
кристалла
с
размерами
шl
= N1al
и
Ш2
= N
2а2
трансформанта
формы
представляет
собой
произведение
двух
членов
вида
(8.11в).
Если
сфера
Эвальда
ПРОХО[l,ит
точно
через
центр
узла
обратной
решетки,
дифракционное
пятно
выглядит
так,
как
показано
на
фиг.
53,
а.
Таким
образом,
дифракция
на
пространственной
решетке
конечных
размеров
аналогична
диф
ракции
Фраунгофера.
Нак
будет
отмечено
дальше,
трансфор
манта
формы
зависит
только
от
размеров
и
формы
объекта,
но не
зависит
от
межатомных
расстояний.
Наули
[20]
использовал
транс
форманту
формы
(8.11в)
для
определения
толщины
тонких
пленок
ZnO.
Для
кристалла
в
форме
маленького
диска
диаметром
w
транс
форманты
формы
выглядят
так,
как
показано
на
фиг.
53, 6.
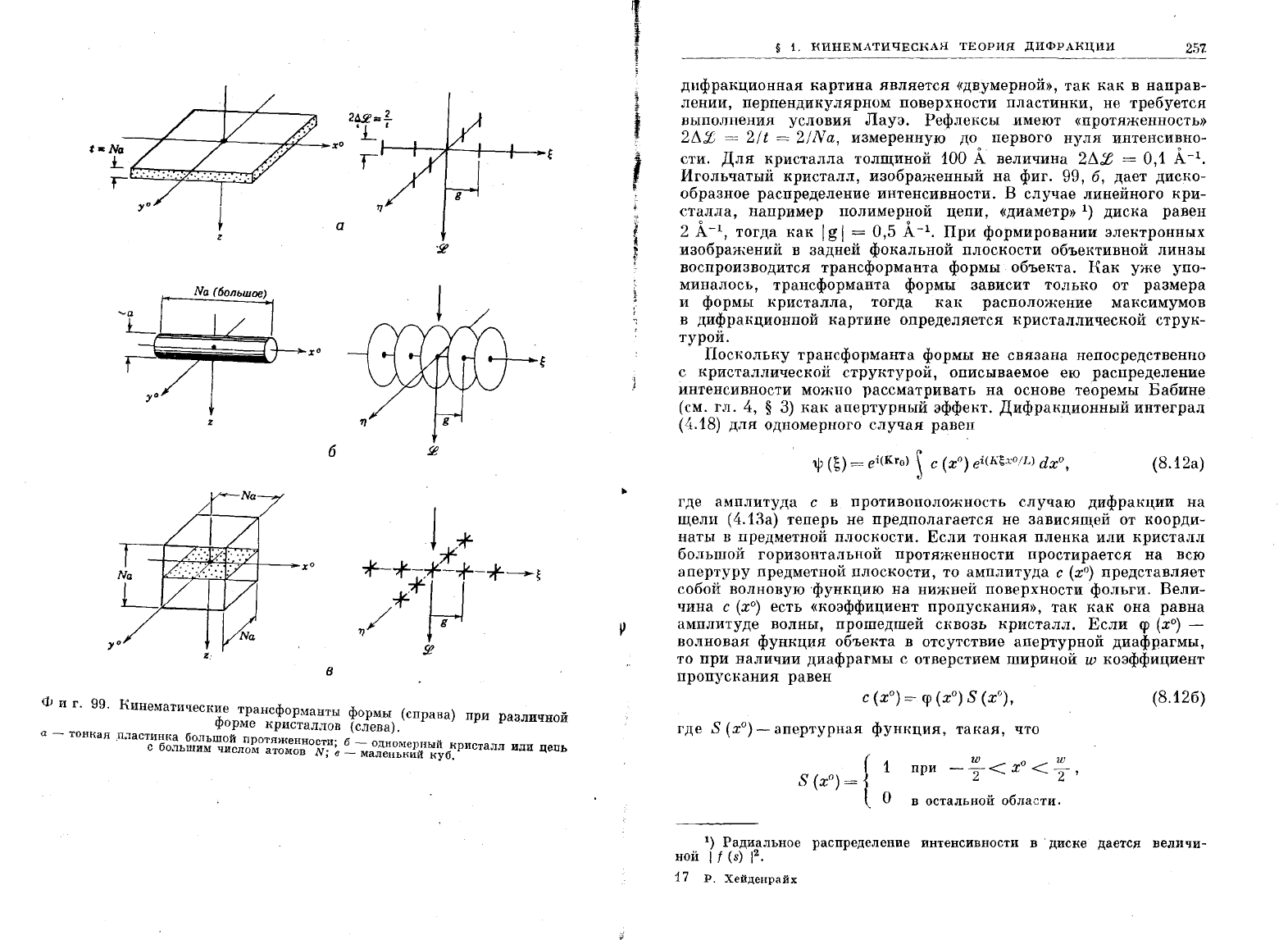
На
фиг.
99
представлено
распределение
интенсивностей
в
обратной
решетке
кристаллов
различной
формы.
Дифракционная
картина,
возникающая
при
рассеянии
волны,
падающей
перпендикулярно
плоскости
(6,
'У)).'
может
быть
приближенно
получена
пересече
нием
областей
вблизи
узлов
обратной
решетки
плоскостью,
парал
лельной
(6,
'У)).
Фиг.
99,
а
соответствует
очень
тонким
кристаллам,
применяющимся
обычно
при
просвечивании;
соответствующая
t
а
Na--.:r----)IL-.---.А:L.._хо
1..
r.-;-."':"""':""r~~"'":"">-r_._.....l".У
Г
~"--'---'-r-~::....;...:...;:.:....:y
z
а
6
в
Фиг.
99.
R'инематичеСRие
трансформанты
формы
(справа)
при
ра:щичной
форме
Rристаллов
(слева).
а
-
ТОНl~ал
плаСтиниа
большой
ПРОТJIЖ
б
.
с
большим
числом
ато';~::О'jJ~'в'
-маодномеР!IЫЙ
бнристалл
или
цепь
, -
леньиии
ну
.
,-
t
f
~
f
i
,
§
t.
НИНЕМАТИЧЕСНАН
ТЕОРИЯ
ДИФРАНЦИИ
2,57
дифракционная
картина
является
«двумерной»,
так
как
в
направ
лении,
перпендикулярном
поверхности
пластинки,
не
требуется
выполнения
условия
Лауэ.
Рефлексы
имеют
<шротяженность»
2/).,;[, =
2/t
=
2/Na,
измеренную
до
первого
нуля
интенсивно-
сти.
Для
кристалла
толщиной
100
А
величина
2/).,:1:,
= 0,1
А
-1.
Игольчатый
кристалл,
изображенный
на
фиг.
99,
б,
дает
диско
образное
распределение
интенсивности.
В
случае
линейного
кри
сталла,
например
полимерной
цепи,
«диаметр»
1)
диска
равен
2
1-1,
тогда
как
I g I = 0,5
А
-1.
При
формировании
электронных
изображений
в
задней
фокальной
плоскости
объективной
линзы
воспроизводится
трансформанта
формы
объекта.
Как
уже
упо~
миналось,
трансформа:нта
формы
зависит
только
от
размера
и
формы
кристалла,
тогда
как
расположение
максимумов
в
дифракционной
картине
определяется
кристаллической
струк
турой.
Поскольку
трансформанта
формы
не
связана
непосредственно
с
кристаллической
структурой,
описываемое
ею
распределение
интенсивности
можно
рассматривать
на
основе
теоремы
Бабине
(см.
гл.
4, §
3)
как
апертурный
эффект.
Дифракционный
интеграл
(1~.18)
для
одномерного
случая
равен
'ф
(~)
=
ei(Kro)
.~
с
(х
О
)
еi(К~хО/Ц
dxo,
(8.12а)
где
амплитуда
с
в
противоположность
случаю
дифракции
на
щели
(4.13а)
теперь
не
предполагается
не
зависящей
от
коорди
наты
в
предметной
плоскости.
Если
тонкая
пленка
или
кристалл
60ЛЬШОЙ
горизонтальной
протяженности
простирается
на
всю
апертуру
предметной
плоскости,
то
амплитуда
с
(х
О
)
представляет
собой
волновую
'функцию
на
нижней
поверхности
фольги.
Вели
чина
с
(х
О
)
есть
(<коэффициент
пропускания»,
так
как
она
равна
амплитуде
волны,
прошедшей
СRВОЗЬ
Rристалл.
Если
<р
(х
О
)
-
волновая
фУНКЦIIЯ
объеRта
в
отсутствие
апертурной
диафрагмы,
то
при
наличии
диафрагмы
с
отверстием
шириной
w
коэффициент
пропускания
равен
(8.126)
где
S
(х
О
)
-
апертурная
функция,
таRая,
что
w w
при
- 2 <
х
О
< 2 '
в
остальной
области.
1)
Радиальное
распределение интенсивности
в'
ДИСRе
даетсд
величи
ной
1 f (s)
12.
17
Р.
Хейденрайх

258
гл.
8.
ИНТЕНСИВНОСТЬ
ДИФРАНЦИИ
Дифракционный
интеграл
(8.12а)
может
быть
теперь
в
виде
+00
'Ф
(s) =
~
ер
(х
О
)
S
(х
О
)
eiK(~xo
jL)
dx
O
,
-00
записан
(8.12в)
Д
г~я
а~~~ит~а
рассеяния
нулевого
а
тома
ехр
i (Kro)
опущена.
у
~
-
s/
L
максимальная
амплитуда
рассеяния
ер
(х
О
)
S
(хО)
равна
как
раз
Nf
(8),
где
число
атомов
N
таково,
что
Na
= w
(а
-
расстояние
между
атомами).
Поведение
'Ф
(s)
вблизи
макси
мума
может
быть
выражено
в
функции
Д
1":
=
Lд
А
С
(8.12в)
находим
(L'Л
~-"
1):
~
fJ·
помощью
+wj2
'Ф
(дs)
= f
(8)
N
~
S
(х
О
)
е
2пЕ
мх
о
dx
O
=
-711/2
- f
(8)
N sin
лwL\~
-
ЛWL\S·
(8.12г)
Ле~ко
видеть,
что
интенсивности
(8
12г)
и
(8
11
)
В
боль
'.
в
совпадают
картин
на~~~~~:й
случаев
при
интерпретации
дифракционны~
интерес
представляют
сведения
о
взаимном
раСположении
кристаллических
ПЛОскостей.
Поэтом
обно
выраз~ить
.
интенсивности
через
структурный
фактор
гру~пь;~лос
~остеи,
про
ходящих
через
все
атомы
одной
элементарной
ячейки-
езультаты,
полученные
для
одномерной
решетки,
в
авноЙ
мере
относятся
и
к системе
плоскостей
(hkl)
с
р
расстоянием
d _ Д
межплоскостным
(
hkl)
hkl
-
а.
ля
кристалла,
имеющего
толщину
w .
в
направлении
нормали
к
плоскостям
(hkl).
Ф
манта
формы
(8.11в)
или
(8.12
г)
равна
'
транс
ор-
'ф
(дS).hkZ
= N F (hkl) sin
ЛW
(hkl)
L\~
(8.13а)
Лw
(hkl)
L\s
'
~~~
~
(hk~)П6Ь
число
групп
плоскостей
со
структурным
факто-
б
.
помощью
СОотношения
(7.8б)
структурный
фактор
может
ыть
выражен
через
коэффициент
Фурье:
NF* (hkl) = N
4~
V
hkZ
•
(8.13б)
Выра~{ение
(8.13а)
удобно
ИСПОльзовать
для
получения
отно-
сительнои
интенсивности
колец
Дебая
Ше
П
не
ни
-
рера.
осле
выпол-
я
интегрирования
по
углам
(21]
от
ная
интенсивность
1 (hkl) / 1
~
носительная
интеграль-
б
о
малои
части
кольца
Д
(отнесенная
к
единице
о
ъема
вещества)
оказывается
равной
[hkl
{F
hk
/2
dh
2
- =
л
2
_l
_k~
(hkl)
л
[о
Q
4лLл
У
L1,
(8.13в)
где
у
(hkl)
-
фактор
повторяемости.
§
1.
НИНЕМАТИЧЕСНАЯ
ТЕОРИЯ
ДИФРАНЦИИ
259
Путем
измерения
относительной
интенсивности
часто
ока
зывается
возможным
установить
наличие
в
поликристаллическом
образце
предпочтительной
ориентации.
В
величинах
относительной
интенсивности
обнаруживается
также
расхождение
между
кине-
матической
и
динамической
теориями
[22].
При
w < 80
А
и
уско
ряющем
напряжении
20-50
кв
рассчитанные
в
кинематическом
приближении
интенсивности
для
алюминия
согласуются
с
экспе-
риментом.
Если
же
w
больше
"",80
А,
требуется
привлечепие
дина
мической
теории.
Для
более
тяжелых
элементов
эта
критическая
толщина
значительно
меньше.
Наличие
различных
структурных
неоднородностей
требует
известной
осторожности
при
интерпре
тации
относительных
интенсивностей
рассеяния
на
поликристал
лических
пленках.
Rимото
[23]
объяснял
аномалии
интенсивно
сти
рассеяния
от
образцов
серебряной
пленки
влиянием
дефектов
упаковки
в
кристаллитах
размером,
примерно
равным
14
A~
Выражение
для
дифракционного
интеграла
для
случая
одного
измерения
(8.12в)
может
быть
обобщено
на
трехмерный
случай.
В
кинематическом
приближении
это
было
сделано
Лауэ
[24],
который
вычислил
распределение
амплитуды
рассеяния
рентге
новских
лучей
около
узлов
обратной
решетки
[25].
Он
назвал
интеграл
Фраунгофера
форм-фактором
кристалла.
Последний
в
точности
соответствует
тому
же
апертурному
эффекту,
который
мы
только
что
рассмотрели
в
одномерном
случае.
Интер
ференционные
функции
(кинематические
трансформанты
формы),
или
форм-факторы
кристалла,
были
подробно
рассчитаны
для
кристаллов
различных
геометрических
форм
и
пространственных
ориентировок
Паттерсоном
[26]
и
Рипчем
(27].
Результаты
расче
тов
справедливы
в
кинематическом
приближении
и
применимы
в
случае
электронной
дифракции
при
размерах
кристаллитов
менее
примерно
60
А.
Таким
образом,
они
имеют
важное
значение
при
изучении
дифракции
от
очень
маленьких
кристаллов
или
групп
атомов.
Внутренние
структурные
нарушения
в
кристаллите
вызы
вают
эффекты
формы
вокруг
узлов
обратной
решетки,
подобные
тем,
которые
обусловлены
форм-фактором.
Если
грань
кристал
ла
параллельна
плоскости
отражения,
в
которой
находится
дефект
упаковки
или
неоднородность,
то
трансформанта
формы
оказы
вается
больше
той,
которая
связана
только
с
конечными
разме
рами
кристалла
или
только
с
неоднородностью.
Часто
бывает
трудно
определить,
связана
ли
наблюдаемая
форма
максимума
в
обратном
пространстве
с
формой
кристалла
или
с
наличием
в
нем
нерегулярностеЙ.
В
таких
случаях
большую
помощь
может
оказать
электронный
микроскоп,
и
именно
при
изучении
дефек
тов
в
кристаллах
электронное
изображение
может
дать
ценную
информацию.
Интерпретацию дифракционной
картины
обычно
17*

260
гл.
8.
ИНТЕНСИВНОСТЬ
ДИФРАНЦИИ
'
'начинают
в
рамках
кинематической
теории,
а
затем
В
случае
необходимости
обращаются
к более
высоким
приближениям.
Дина
мические
трансформанты
формы
могут
значительно
отличаться
от
кинематических.
Методы
преобразования
Фурье
в
применении
к
анализу
данных
электронной
дифракции
весьма
подробно
рас
смотрены
Каули
и
Рисом
[28].
Интересно
рассмотреть
трехмерныIй
вариант
выражения
(8.12в):
чr
(1;,
11,
.z)
=
+00
=
~ ~
~
'Ф(х
О
,
уО,
ZO)S(XO,
уО,
ZO)
ехр
[2лi
(1;х
О
+ 11yo+XzO)]dxOdyOdzO,
(8.14а)
где
'Ф
(х
О
,
уО,
ZO)
-
отношен:це
волновых
функций
выходящего
и
пад«;tющего
пучков,
1;,
11,
Х
-
координаты
в
обратной
решетке
,(положено
Lл
= 1).
Если
известна
Ч'
(1;,
rl,
Х),
то
'Ф
(Х
О
,
уО,
ZO)
легко определяется
обращением
соотношения
(8.14а),
так
как
ч'
и
'ФS
связаны
преобразованием
Фурье.
На
дифракционной
кар
тине
наблюдается
им.енно
!
Ч'
I
2,
И поэтому
никакая
информация
о
знаках
и
фазах
не
может
быть
получена.
В
случае
электронной
~ифра.RЦИИ,
когда
радиус
сферы
Эвальда
значительно
больше
,расстояния
между
ближайшими;
узлами
обратной
решетки,
выра
жение
(8.14а)
может
быть
приведено
к
двумерному
виду.
Пусть
u
объект представляет собой
кристаллическую
пластинку
то.дщи;нои
t
С
ZO
= t,
лежащую
в
предметной
плоскости.
Коор
дината
обратной
решетки
.z
направлена
вдоль оптическоЙ
оси.
Еслц
взять
отдельный
узел
обратной
решетки,
то
отклонение
сфер~
Эвальда
от
этого
узла,
как
и
раньше,
равно
~.
Для
про
стоты
будем
прибллженно
считать
сферу
Эвальда
плоскостью
и
примем,
что
~
~
О.
Равенство
(8.14а)'
примет
теперь
такой
же
вид,
Kfl,K
и
В
случае
двумерной
дифракции:
+00
ч'
(~,
11)
=
~
~
'Ф
(хО,
уО,
t)
S
(х
О
,
уО)
ехр
[2лi
(1;х
О
+
11уО)]
dx
o
dyo.
~OO
(
(8.14б)
Несмотря
на
интегральную
форму
выражения
(8.14б),
основная
,проблем<:t
остается
прежней
-
найти:
волновую
функцию
в
кри
сталле
'Ф
(х
о
,
уО,
t).
Если
выходящая
волна
является
решением
уравнения
Ш
ре
дингера,
то
мы
им'еем
случай
тонкой
пленки
с
постоянным
ПQтец
циалом
внутри,
равным
V
o
,
рассмотренный
в
гл.
5.
Как
сле
дует
из
,соотношения
(5.15),
(8.14в)
§
2.
ДВУХВОЛНОВАЯ
ДИНАМИЧЕСRАЯ
ТЕОРИЯ
261
Единственным
узлом
обратной
решетки,
характеризующим
выхо
дящую
волну,
является
g =
О,
а
форма
максимума
будет
опреде
ляться
дифракцией
Фраунгоq
ер
1
на
границах.
Каули
и
Муди
[29]
в
первом
приближении
предположили,
что
толщина
пленки
t
очень
мала
и
равна,
например,
~ZO.
Тогда
амплитуда
выходя-
щей
волны
равна
(
О О
) 1
+.
nV
~
О
Q
~
О
ер
x,y,t
~
~
л'vа
z
-2
z.
(8.14г)
в
следующем
приближении
будем
считать,
что
V
не
постоянно.,
т.
е.
V = V
(х
О
,
уО,
ZO),
и;
выберем
~ZO
достаточно
малой,
чтобы
изменение
V
по
толщине
~ZO
было
слабым.
Подстановка
(8.14г)'
в
(8.14б)
приводит
к
интегралу,
похожему
на
полученный
Каули
и
Муди.
Но
в
отличие
от
последних
мы
не
учитывали
кривизны
сферы
Эвальда.
При
использовании
аппроксимации
(8.141')
BC~:
сводится
К
суммированию
вкладов
в
рассеяние
слоев
ТОЛЩИНОИ
i
~ZO
дЛЯ
получения
интенсивности
от
толстого
образца.
В
случае:
кристалла
толщиной
t
интенсивнОсть
в
пренебрежении
потеРЯМIL
(Q
/2) t
должна
иметь
примерно
такой
вид:
I
ер
\2
'-' 1 _
(:~
t)
2 •
Если
потребовать,
чтобы
отклонение
от
интенсивности,
соот
ветствующей
экспоненциальной
зависимости
(8.14в),
не
превы
шало
10%,
то
для
t
получаем
условие
t~<0,3
(
л:v~
).~
Для
электронов
с
энергией
100
1'iэв
произведение
лЕ
=
406~
и
если
V
o
""
10
эв,
то
при
указанной
точности
t
не
должно
превы-:
шать
40
А.
Это
требование,
по-видимому,
эквивалентно
оснрв-
,
ным
предположениям
кинематической
теории.
Rаким
образом
рас
смотренное
приближение
приводит
к
результатам
двухволновой
динамической модели для
более
толстых
кристаллов,
удовлетво-,
ряющим
уравнению
Шредингера
и
граничным
условиям,
просле-,
дить
трудно.
§ 2.
Двухволновая
динамическая
теория
Динамическая
теория,
получила
свое
название
в'
оригина.лъ-~
ной
работе
Эвальда
[30],
посвященной
дифракции
рентгеновских,
лучей.
Это
назваНJIе
очень
удачно,
так
как
оно
описывает
обмен
энергией
между
дифрагированной
и
проходящей
волнами.
В
мате,,;.
матическом
отношении
задача
о
дифракции
аналогична
зада:Ч~i
о
линейных
колебаниях
связанных
осцилляторов.
Rолебав;и~
двух
простых
связанных
маятников,
:когда
кинетическ~я
Эn;~рl
,и.~
