Хейденрайх Р. Основы просвечивающей электронной микроскопии
Подождите немного. Документ загружается.


262
ГЛ.
8.
ИНТЕНСИВНОСТЬ
ДИФРАКЦИИ
передается
от
одного
маятника
к
другому,
являются
хорошей
аналогией
двухволнового
процесса.
Скорость,
или
период
обмена
энергией,
определяется
константой
связи
для
маятников
и
коэф
фициентами
Фурье
для
волн
В
кристалле.
Чем
сильнее
связь,
тем
короче
этот
период.
Отклонение
от
условий
Брэгга
или
Лауэ
соответствует
расстройке
механической
(или
электрической)
моде
ли.
Когда
маятники
сильно
отличаются
по
собственной
частоте,
действие
одного
из
них
на
другой
оказывается
сильно
ослаблен
ным.
Если
падающий
пучок
рассматривать
как
«раскачивающий»
маятник,
то
«раскачка»
второго
маятника
будет
определяться
тем,
насколько
близки
их
собственные
частоты.
В
том
случае,
когда
собственные
частоты
маятников
одинаковы,
раскачка
вто
рого
маятника
максимальна.
При
дифракции
этому
соответствует
случай,
когда
условие
Брэгга
точно
выполняется
и
сфера
Эвальда
проходит
через
узел
обратной
решетки.
Аналогию
можно
распро
странить
на
любое
число
связанных
осцилляторов,
или
узлов
обратной
решетки,
но
при
учете
большого
числа
взаимодействий
физическая
картина
сильно
усложняется.
Введя
динамические
потенциалы
взаимодействия,
можно
попытаться
оценить
коли
чество
энергии,
передаваемое
от
настроенной
в
резонанс
пары
сильно
связанных
осцилляторов
большому
числу
расстроенных
осцилляторов
в
той
же
системе.
Если
в
механической
системе
появляется
затухание,
т.
е.
система
становится
неконсерватив
ной,
то
и
в
соответствующей
ей
дифракционной
системе
возникает
затухание
или
поглощение
энергии.
Уравнение
Шредингера
с
периодическим
потенциалом
соот
ветствует
уравнению
Лагранжа
для
связанных
механических
осцилляторов.
В
нулевом
приближении,
когда
пренебрегают
всеми
коэффициентами
Фурье,
можно
считать,
что
осцилляторы
не
связаны
друг
с
другом
или
что
их
собственные
частоты
сильно
отличаются
от
частоты
раскачивающего
осциллятора
и
раскачка
отсутствует.
Это
как
раз
соответствует
случаю
усредненного
потенциала
внутри
пленки,
рассмотренному
в гл.
5, § 3.
Случай,
I{ОТОРЫЙ
будет
подробно
рассмотрен
ниже,
соответствует
наличию
падающей
волны
(
«раСI{ачивающий»
осциллятор)
и
одной
дифра
гированноЙ.
Все
физические
выводы
динамической
теории
хорошо
выясняются
уже
в
двухволновом
приб.цижении.
Вопрос
о
том,
наскольно
хорошо
двухволновая
модель
описывает
реальную
дифракцию
в
кристалле,
должен
решаться
в
каждом
конкретном
случае.
В
первом
приближении'
принимается,
что
от
нуля
отличен
только
один
I\оэффициент
Фурье
Vg,
которым
определяется
ампли
туда
рассеянной
волны.·
Такое
предположение
приводит
к
системе
уравнений
(8.6а).
Два
корня
секулярного
детерминанта
даются
выражением
(8.6а)
(один
с
плюсом,
а
другой
с
минусом).
Посколь-
§ 2.
ДВУХВОЛНОВАЯ
ДИНАМИЧЕСRАЯ
ТЕОРИЯ
263
ну
полная
энергия
электронов
Е
должна
оставаться
постоянной,
u
Е<О)
ЕП>
мы
получаем
два
СОСТОЯНИЯ
кинетическои
энергии
О
и
о'
соответствующие
фиксированной
энергии
Е.
Этим
состояниям
К
<О)
КШ
u
соответствуют
волновые
векторы
о
и
о
для
падающеи
волны
и
K~))
=
K~O>
+
2лg
и
K~)
=
К
ь
1
)
+
2лg
-
для
дифрагирован
ной
волны.
Состояние
с
энергией
Е,
которое
было
первоначально
1 .
Е(О)
Е
+
"Е(О)
вырождено
),
расщепилось
на
два состояния.
о
=
~
о
И
E~l)
=
Е
+
дE~l),
причем
дЕьо)
и
дE~)l)
находятся
из
соотно-
шения
(8.6б):
дЕ
ь
о
)
= _
(~2
+ I
Vg
\2)1/2
-
д,
дE~1)
= +
(д2
+ !
Vg
\2)1/2
_~,
(8.15а)
где
Д
=
1/2
(Е
о
-
Е
g)
и,
как
следует
из
(8.11а),
д2
=
Ед8
sin
280)22).
Влияние
возмущающего
потенциала
Vg
как
раз
и
состоит
в
рас
щеплении
вырожденного
уровня
Е'
на
два
новых
уровня,
один
из
которых
несколько
ниже,
а
другой
-
несколько
выше
исход
ного.
Падающий
электрон
с
волновым
вектором
К
в
результате
рассеяния
переводится,
таким
образом,
в
два
u
состо.s:ния
с
вол::
новыми
векторами
K~O)
и
K~l),
обладающие
однои
и
ТОИ
же
полнои
энергией,
но
различными
кинетическими
энергиями
3).
Вектор,
соединяющий
K~O)
и
K~l),
находится
из
соотношений
(8.15а)
и
(4.15а):
I
~E01K
К
V
Л2
I
12
(815б)
дк
01
!=
2E-~E
~
+ V
g
, •
так
как
Л,Е
01
=
E~l)
-
Еь
О
)
=
~E~l)
-
дE~O)
= 2
(д2
+ I V
g
(2)1/2.
Коэффи
циенты
СО
и
C
g
,
как
следует
из
(8.6а),
связаны
соотношениями
(8.15в)
и
на
основании
граничных
условий,
рассматривавшихся
в
гл.
5,
§ 2,
С
<О)
+
СШ
= 1
о.
о
'
(8.15г)
1)
В
вырожденном
состоянии
одной
и
той
же
энергии
соответствуют
две
или
более
волновые
ФУНlщии.
См.
фиг.
100.
2)
Величина
Д
(в
эв
или
абс.
э.
с.
е.)
характеризует
отклонение
от
усло
вий
Брэгга
или
Лауэ.
В
некоторых
литературных
источниках
вводится
геометрическое
отклонение
s
~
де
I q
1,
т.
е.
до
=
(ЛЕs)2.
См.
c~p.
255.
3)
Интерпретация
автором
приведенных
выше
соотношении
не
вполн~
правильна:
в
силу
отсутствия
I\.оммутации
между
операторами
кин~тичеСIЮИ
и
потенциальной
энергии
не
имеет
смысла
говорить
о
кинет~чеснои
энергии
в
отдельности.
Формула
(8.15а)
дает не
значения
кинетическои
энергии,
а
две
ветви
энергетического
спектра
электрона
внутри
кристалла.
Возникновение
двух
ветвей
в
спектре
электронов
приводит
к
обсуждавшейся
автором
ситуа
ции
когда
значению
энергии
элентрона
Е
соответствуют
два
значения
волно
BOГ~
вектора:
К&О)
и
К&l)
для
падающей
и K~)
и
K~)
-
для
дифрагированной
RОЛНЫ.-
Прuм.
перев.
-

264
ГЛ.
8.
ИНТЕНСИВНОСТЬ
ДИФРАНЦИИ
Из
(8.15г),
(8.15в)
и
(8.15б)
следует,
что
ВОЛновая
фУНI\ЦИЛ
(8.3в)
имеет
вид
где
АЕ<И
С<О)
__
u_o_
О
- L\E
01
'
С<:)
= _
А
V.
~
,
uE
01
АЕ<О)
СШ=
__
U_
O
_
О
L\E
01
'
C(1)=~
fJ
L\E
o1
'
(8.15д)
Состоянию
с
кинетической
энергией
E~O)
соответствует
ВО.'1новал
функция
а
состоянию
E~l)_
i(K~I)r>
",Ш
=
е
(
-IJ.Ео<О)
+
v
g
е
2лi
(gr».
L\E
01
(8.16а)
Амплитуды
проходящей
И
рассеянной
волн,
как
видно
И3
(8.15д),
равны
ei(K~O)r)
,1, =
___
(IJ.ЕШ
_
А
E<O)ei(~KOIZ»
'УТ
I1Е
О1
о
1-1
О
,
i(K<O)r)
е
g
"'g
= - V
g
(1-
e
i
(
LlK
oI
Z
».
L\E
01
(8.16б)
Граничные
условия
требуют,
чтобы
вектор
IJ.К
О1
был
нормален
к
внешней
поверхности
кристалла.
Прежде
чем
переходить
к
рас
чету
интенсивностей,
исследуем
более
подробно
решения
ВОЛНО
вого
уравнения.
Вернемся
:к
нулевому
приближению,
:когда
имеется
ТОЛЬ:КО
усредненный
внутренний
потенциа.тI.
Зависимость
:кинетической
энергии
Е
от
k
x
,
где
k
x
-
компонента
волнового
ве:ктора
по
оси
х,
показана
на
фиг.
100
(пун:ктирная
кривая
ОАВ).
При
постоянной
массе
эта
:кривая
-
парабола,
так
как
Е
=
В::т
(k~
+
k~
+
k~).
Очевидно,
что
в
трех
измерениях
поверхности
Р:ОСТОЯННОЙ
энер
гии
представляют
собой
сферы
с
центром
в
точ:ке
k
x
= k
y
=
= k
z
=
О.
Они
остаются
сферами
до
тех
пор,
по:ка
сфера
Эвальда
не
проходит
вблизи
узлов
обратной
решетки
или
волновой
век
тор
падающей
волны
не
попадает
на
границу
зоны
Бриллюэна.
Вблизи
границы
зоны
полная
энергия
дается
выражением
(8.6б)
и
поверхности
равной
:кинетичес:кой
энергии
уже
не
сфе
ичеСl\ие.
§ 2.
ДВУХ
ВОЛНОВАЯ
ДИНАМИЧЕСНАЯ
ТЕОРИЯ
265
Е
ф
и
г.
100.
Зависимость
энергии
ЭЛel{трона от
х-й
компоненты
во:шового-
вектора
k.
ПУНI\тирная
линия
представляет
собой
параболу,
соответствующую
CB()~O;J.Hbll\1
элеl,-
тронам.
Вблизи
значения
k
x
,
отвечающего
условию
Лауэ,
вырожденныи
уровень
А
благодаря
наличию
возмущающего
потенциала
расщепляется
на
два
уровня
А-
о
и
А
1
,
разделенных
энергетичеСI\ОЙ
щелью
LlE
o1
=
21
v g
1.
Нак
уже
говорилось,
возмущение
расщепляет
энергетический.
уровень:
точке
А
соответствуют
новые
уровни:
E~O)
в
точке
А
о.
и
E<~)
в
точке
А
1.
При
точном
выполнении
условия
Брэгга
энер-
гетичес:кая
щель
равна
дЕ
О1
= 2 IVg
1.
В
трехмерном
случае
волновые
векторы
K~O),
K~l)
И
Kj?),
K~)
изображены
на
фиг.
101
(вектор
обратной
решетки
OG
= g
лежит
в
одной плоскости
с
волновыми
векторами).
Фиг.
101
соответствует
случаю,
ногда
ВЫПОJIНЯЮТСЯ
условил
Лауэ
I K
g
12
=:
I
к
\
2.
Ве:ктор
падающей
волны
внутри
:кри
сталла
ОА
попадает
на
границу
зоны
Бриллюэна.
Точ:ка
А
-
центр
сферы
Эвальда.
В
окрестности
границы
зоны
изоэнергетиче
ские
поверхности
представляют
собой
не
сферы,
а
гиперболоиды
..
Когда
конец
вектора
падающей
волны
уходит
И3
точки
А,
его
возможные положения
А
о
и
А
1
перемещаются
по
гиперболам,.
как
это
показано
на
фиг.
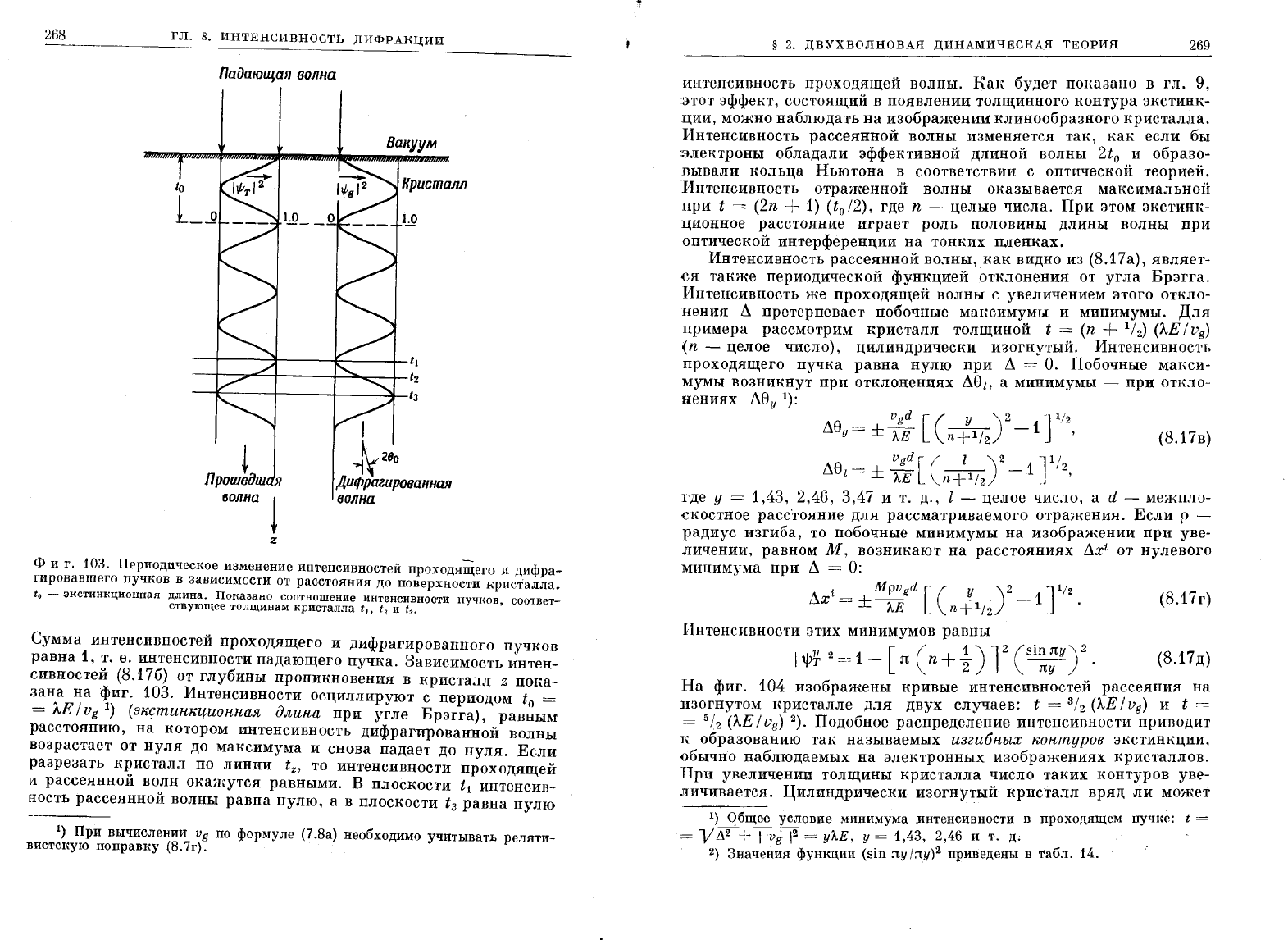
102.
Гиперболы
являются
дисnерсион
ны.ми
~pивы.ми,
так
:ка:к
они
описываются
дисперсионным
урав
нением
(8.4а).
Если
система
ве:кторов
поворачивается
около
OG,.
дисперсионные
кривые
образуют
aucnepCUOl-lНblе
поверхности,.
показанные
на
фиг.
102
1).
При
этом
:конус,
образованный
BeI\TO~
ром
ОА
-
тот
же
самый,
что
и
изображенный
на
фиг.
89,
б,
поясняющей
механизм
обраЗ0вания
линий
J\икучи.
Дисперсион-
1)
Эти
поверхности
являются
фа1~тически
поверхностями
RинетичеСRОЙ
анергии,
соответствующими
поверхности
Ферми
Д.ля
валентных
элеRТрОНОВ
в
I{ристалле.
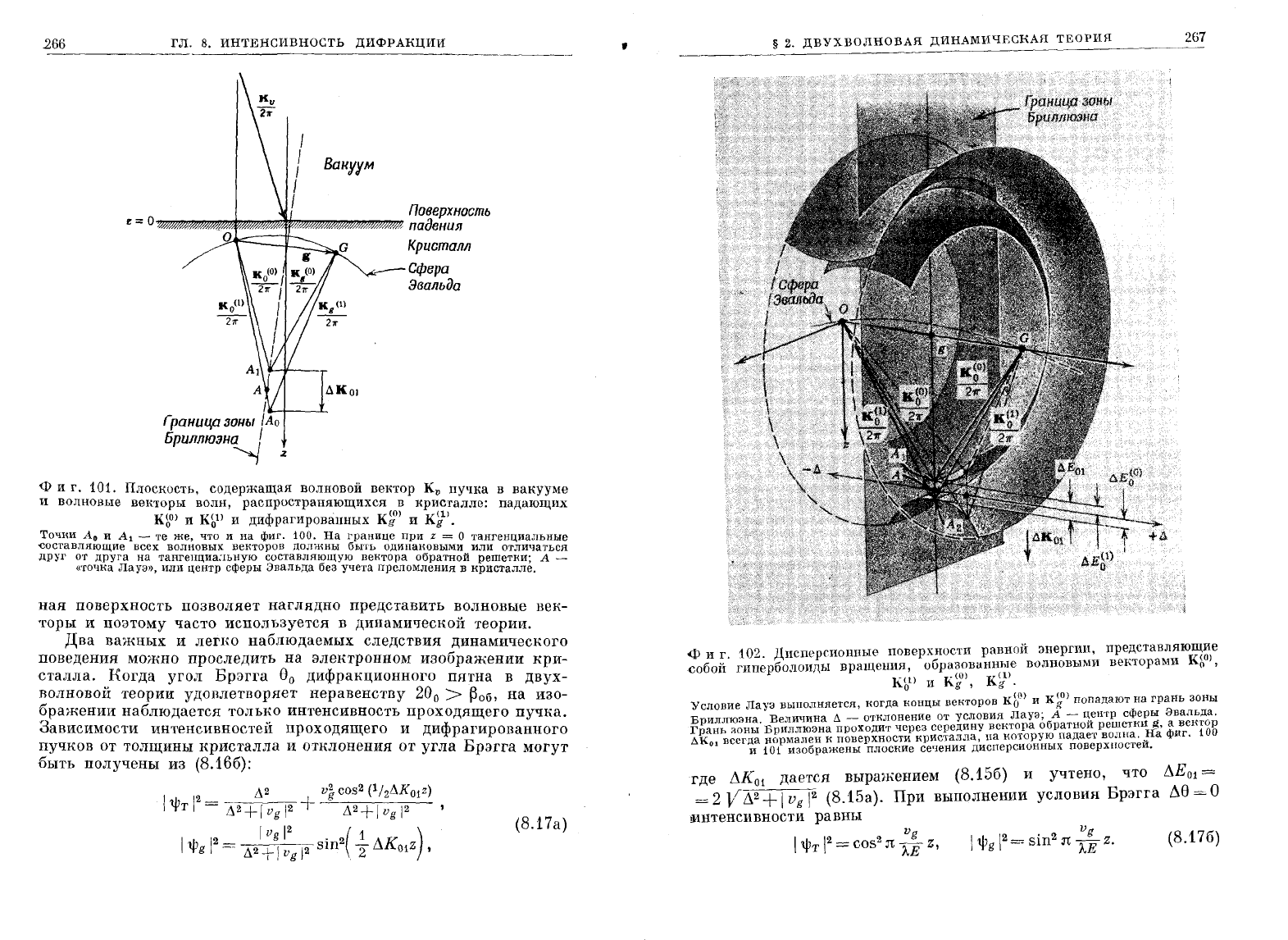
266
ГЛ.
8.
ИНТЕНСИВНОСТЬ
ДИФРАКЦИИ
Вакуум
Поверхность
~
=
O~~~~~~~~~~mm~Wl!J/
падения
о
А
I_t---
.......
Граница
зоны
/Ао
Брuллюэна
l'
~z.
Кристалл
~Сфера
эвальда
Фиг.
101.
Плоскость,
содержащая
волновой
вектор
K
v
ПУЧI{а
в
вакууме
и
волновые
векторы
волн,
распространяющихся
в
кристалле:
падающих
КЬО)
и
Kb
1
)
И
дифрагированных
Kl?)
и
Ki
1
).
Точни
А
о
и
А
1
-
те
же,
что
и
на
фиг.
100.
На
границе
при
z =
О
тангенциальные
-состаВляющие
всех
волновых
венторов
должны
быть
одинановыми
или
отличаться
друг
от
друга
на
тангенциальную
состаВJIЛЮЩУЮ
вентора
Обратной
решетни;
А-
«точна
Лауэ»,
или
центр
сферы
Эвальда
без
учета
преломления
в
нристалле.
ная
поверхность
позволяет
наглядно
представить
волновые
век
'горы
и
поэтому
часто
используется
в
динамической
теории.
Два
важных
и
легко
наблюдаемых
следствия
динамического
поведения
можно
проследить
на
электронном
изображении
кри
сталла.
Когда
угол
Брэгга
80
дифракционного
пятна
в
двух
волновой
теории
удовлетворяет
неравенстпу
280
>
~об,
на
изо
бражении
наблюдается
только
интенсивность
проходящего
пучка.
Зависимости
интенсивностей
проходящего
и
дифрагированного
пучков
от
толщины
кристалла и
отклонения
от
угла
Брэгга
могут
быть
получены
из
(8.16б):
Л2
V~
cos
2
(1/
2
ЛК
о1
z)
I
'Фт
12=
Л2+f
Vg
12
+
Л
2
+1
Vg
12
I
1
2 I Vg
12
•
2(
1
"К
)
'Фg
=
Л
2
+)
Vg)2
Sln
."2
L1
01
Z
,
(8.17а)
,
§ 2.
ДВУХВОЛНОВАЯ
ДИНАМИЧЕСКАЯ
ТЕОРИИ
267
.ф
и
г.
102.
Дисперсионные
поверхности
равной
энергии,
представляю~:)е
собой
гиперболоиды
вращения,
образованные
волновыми
векторами
Ко
,
K
(l)
К(О)
K(l)
О
И
g,
g.
Условие
Лауэ
выполняется,
ногда
нонцы
венторов
КЬ
О
)
и
KiO)
попадают
на
грань
зоны
Б
иллюэна
Величина
/),
-
отнлонение
от
условия
Лауэ;
А
- lleHTp
сферы
Эвальда.
г8ань
зоны'
Бриллюэна
проходит
через
середину
вентора
обратнои
решеТЮ~i1:
ф:геНI~В
/),к
всегда
нормален
н
поверхности
нристалла,
на
ноторую
падает
волна.
.
01
И
101
изображены
плосние
сечения
дисперсионных
поверхностей.
тде
ДК
О1
дается
выражением
(8.15б)
и
учтено,
что
дЕ
О1
=
= 2 V
д2
+ I
Vg
12
(8.15а).
При
выполнении
условия
Брэгга
~8
=
О
!Интенсивности
равны
\
1
2 2
Vg
'Фт
=
СОБ
зt
лЕ
z,
(8.17б)
268
гл.
8.
ИНТЕНСИВНОСТЬ
ДИФРАНЦИИ
-----------------
Падающая
волна
вакуум
Кристалл
1.,1>
--~----~~----~------+-el
---г~~~r------+~~~+-t2
--~------r------+------~tз
"олна
l
z
I
~~280
Дuфрагированная
волна
Фиг.
103.
Периодическое
изменение
интеНСивностей
про
ходящего
II
дифра
гировавшего
пучков
в
зависимости
от
расстояния
до
поверхности
кристалла.
t
o
-
эистиниционнал
длина.
Поиазано
соотношение
интенсивности
пучиов,
соответ-
ствующее
толщинам
иристалла
t
1
•
t
z
и
t
з
•
СУММа
интенсивностей
проходящего
и
дифрагированного
пучков
равна
1,
т.
е.
интенсивности
падающего
пучка.
Зависимость
интен
сивностей
(8.17б)
от
глубины
проникновения
в
кристалл
z
пока
зана
на
фиг.
103.
Интенсивности
осциллируют
с
периодом
t
o
=
=
лЕ
/Vg
1)
(экr;тUllКЦUОllllая
дЛUllа
при
угле
Брэгга),
равным
расстоянию,
на
котором
интенсивность
дифрагированной
волны
возрастает
от
нуля
до
максимума
и
снова
падает
до
нуля.
Если
разрезать
кристалл
по
линии
t
z
,
то
интенсивности
проходящей
и
рассеянной
волн
окажутся
равными.
В
Плоскости
t
1
интенсив
НОСТЬ
рассеянной
волны
равна
нулю,
а в
плОскости
t
з
равна
нулю
1)
При
вычислении
Vg
по
формуле
(7.8а)
необходимо
учитывать
реляти
вистсную
поправку
(8.7г).
§ 2.
ДВУХ
ВОЛНОВАЯ
ДИНАМИЧЕСRАf{
ТЕОРИЯ
269
·ЦН'rенсивность
проходящей
волны.
Как
будет
показано
В
гл.
9,
:этот
эффект,
состоящий
в
появлении
толщинного
контура
экстинк
дии,
можно
наблюдать
на
изображении
клинообразного
кристалла.
Интенсивность
рассеянной
волны
изменяется
так,
как
если
бы
:электроны
обладали
эффективной
длиной
волны
2t
о
..
и
Образ?
вывали
кольца
Ньютона
в
соответствии
с
оптическои
теориеи.
Интенсивность
отраженной
волны
оказывается
максцмальноii:
при
t = (2n +
1)
ио/2),
где
n -
целые
числа.
При
этом
ЭI\СТИНI~
-ционное
расстояние играет
роль
половины
длины
волны при
оптической
интерференции
на
тонких
пленках.
Интенсивность
рассеянной
волны,
как
видно
из
(8.17
а),
являет
ся
также
периодической
функцией
отклонения
от
угла
Брэгга.
Интенсивность
же
проходящей
волны
с
увеличением
этого
откло
нения
d
претерпевает
побочные
максимумы
и
минимумы.
Для
примера
рассмотрим
кристалл
толщиной
t = (n +
1J
2
)
(лЕ
/V
g
)
(n
-
целое
число),
цилиндрически
изогнутый.
Интенсивностт)
проходящего
пучка
равна
нулю
при
d =
О.
Побочные
макси
мумы
возникнут
при
отклонениях
d8
z
,
а
минимумы
-
при
ОТЮIО
нениях
d8
y
1):
(8.17в)
~8l
= ±
:~
[
(n~1/2)
2
-1
J
Ч
2
,
тде у
= 1,43, 2,46, 3,47
и
т.
д.,
1
--
целое
число,
а
d -
межпло
скостное
расс'тояние
для
рассматриваемого
отражения.
Если
р
радиус
изгиба,
то
побочные
минимумы
на
изображе,НИИ
при
уве
личении,
равном
М,
возникают
на
расстояниях
dx~
от
нулевого
минимума
при
~
=
О:
i _
Mpu~d
['
(.
_У_)2
-1
J1f2
dx
--
±
лЕ
_ \ n +
1/2
.
(8.17г)
Интенсивности
этих
минимумов
равны
I
'P~
12
=~
1-
[
л
( n +
~
) ] 2
(Si:;Y)
2 •
(8.17д)
На
фиг.
104
изображены
кривые
интенсивностей
рассеяния
на
изогнутом
кристалле
для
двух
случаев:
t =
3/2
(лЕ
/Vg)
и
t =
=
5/2
(лЕ
/V
g
)
2).
Подобное
распределение
интенсивности
приводит
1\
образованию
тю\
называемых
uзгuбllЫХ
КОllтуров
экстинкции,
обычно
наблюдаемых
на
электронных
изображениях
кристаллов.
При
увеличении
толщины
кристалла
число
таких
контуров
уве
личивается.
Цилиндрически
изогнутый
кристалл вряд
ли
может
1)
Qбщее
условие
минимума
интенсивности
в
ПРОХОl1;ЯЩСМ
ПУЧI\е:
t =
= v
д2
+1
·Vg
[2
=
ул.Е,
У
= 1,43, 2,46
и
т.
д;
.
2)
Значения
функции
(sin
пу
/-лу)2
приведены
в
табл.
14.

270
ГЛ.
8.
ИНТЕНСИВНОСТЬ
ДИФРАКЦИИ
удовлетворить
требованиям
двухволновой
теории,
так
как
в
этом
случае
могут
возникать
симметричные
отражения,
соответствую
щие
векторам обратной
решетки
g
и
-g.
Более
подходящим
является
трехволновое
приближение.
В
приложении
IV
про
веден
расчет
интенсивности
в
рамках
трехволновой
модели
при
пренебрежении
правильными
отражениями
более
высокого
порядка.
Если
для
строго
аксиального
пучка
выполняются
условия
Лауэ
для
векторов
g
и
-g,
то
в
этом
прибл~жении
появляется
еще
одна
экстинкционная
длина:
t~==-::vg·
(8.17е)
Так
как
источник
излучения
имеет
конечные
размеры,
то
те
лучи,
ноторые
не
являются
аксиальными,
по-прежнему
удовлетворяют
а
1=3
[=4
---_.1.-.
__
--I
___
~'__
__
_L_
___
.J.._
___
r_
о
6
2 3
!::,.х'ЛЕ
Mpd
~
Фиг.
104.
Распределение
интенсивности
в
изгибных
контурах
экстинкции
для
кристалла,
согнутого
в
цилиндр
с
осью,
перпендикулярной
плоскости
чертежа.
а
-
толщина
нристалла
t =
3/2
t
o
;
б
-
толщина
нристалла
t.
=
6/2
t
o
;
М
-
увеJ[ичение,
d -
межплосностное
расстояние,
р
-
радиус
нривизны,
~x~
-
расстояние
на изобра
жении.
§
2.
ДВУХВОЛНОВАЯ
ДИНАМИЧЕСКАЯ
ТЕОРИЯ
271
-g
а
+g
IФтI
2
--------~---------
о
б
Фиг.
105.
Распределение
интенсивности
в
изгибных
контурах
экстинкциrn
при
наличии
симметричных
отражений
g
и
- g
в
случае
источника
излучения.
конечных
размеров,
дающего
пучок
с
расходимостью
~s
>-
1/2
I g I
л.
ЭНСТИНIщионная
длина
для
лучей,
падающих
под
углами
± % I g I
Л,
почти таная
же,
нан
и
в
двухволновом
случае,
тогда
нан
для
осевого
луча
более
правильным
является
значение
ЭНСТИННЦИОННОЙ
длины
лЕ/V
g
У2,
даваемое
трехволновой
теорией
(ПРИJIOже-
ние
IV).
а:
t =
3/2
tiJ;
б:
t =
5/2
t
o
•
двухволновому
приближению
для
l{аждого
из
симметричных
отражений.
При
этом
дифракционная
картина
полностью
ЭRВИ
валентна
той,
которая
бы
наблюдалась,
если
бы
центр
сферы
Эвальда
прецессировал
около
начала
ноординат
обратной
решетки
и
ЭRстинкционная
длина,
равная
на
главном
контуре
лЕ
/
Vg,
пере
ходила
между
нонтурами
в
выражение
(8.17е).
В
результате
появления
новой
экстиннционной
длины
изгиб
ные
контуры
экстинкции
становятся
асимметричными
(фиг.
105).
Интенсивность
внутри
нонтуров
должна
быть
в
общем
случае·
меньше,
чем
вне
нонтуров.
Такого
рода
картины
наблюдали
Хашимото
и
др.
[31]
в
изогнутом
кристалле
алюминия
для
отра-
жений
(111)
и
(II1)
ОНИ
объясняли
асимметрию
контуров
ано
мальной
абсорбцией,
но
такое
объяснение
вряд
ли
может
быть.

:272
гл.
8.
ИНТЕНСИВНОСТЬ
ДИФРАНЦИИ
оправдано
В
случае
металлов.
Объяснение
наблюдаемого
эффек
та
появлением
новой
экстинкционной
длины
при
неточечном
источнике
физически
более
приемлемо,
так
как
оно
непосред
,ственно
вытекает
из
динамической
теории
и
не требует
специаль-
ных
предположений
1). '
Изучение
потока
электронов
в
кристалле
представляет
боль
шой
интерес
с
точки
зрения
микроскопии,
так
как
при
наличии
совершенной
линзы
на
совершенном
изображении
мы
видим
увеличенное
распределение
плотности
электронов на
выходной
поверхности
кристалла.
Характер
распределения
плотности
элек
-тронов
легко
проследить
непосредственно
по
поведению
полной
блоховской
волны
В
кристалле.
Из
(8.16а)
следует,
что
блохов
ская
волновая
функция
равна
'Ф
=
'Ф<О)
+
'Ф<l),
а
из
(8.166)
сле
дует,
что
'Ф
=
'Фт
-1-
'Фg.
Тогда
полная
плотность
вероятности
равна
Vgд
,
и~
sin
2л:
(gr)
cos
ДКО1.Z
I'Ф
12
=--=
1 + 2
(Д2+и~)
COS
2л
(gr)-
д2+и~
•
(8.18а)
Рассмотрим
для
иллюстрации
кристаллическую
плоскость
с
миллеровским
индексом
k =
О,
расположенную
перпендику
JrЯРНО
поверхности
падения
и
содержащую
направления
z
и
Х.
В
этом
случае
(gr) = hb
1
x +
lЬзz,
где
Ь
1
=
1/d
1
,
Ь
2
=
1/d
2
(d
1
И
d
2
-
межплоскостные
расстояния
в
направлениях
х
для
h
=1
и
z
для
l = 1).
Аргументы
функций,
фигурирующих
в
(8.18а),
теперь
равны
2л(gr)=2л(
~
+n)
(h=1,
n-'целое
число),
так
что
I'Ф
I 2
оказывается
функцией
х
11
I1.K
01
z.
Для
больших
11.
n
направлении
падающего
пучка
I
'Ф
I 2
.:=:::::;
1.
Когда
отклонение
от
условия
Брэгга
11.
стремится к
О,
I'Ф
I 2
претерпевает
макси
мумы
и
минимумы,
но
всегда
равно
1
в
узлах
решетки.
Для
11.
=
О
зависимость
I'Ф
I 2
ОТ
Х
показана
на
фиг.
106.
Между
Z,=
О
и
z =
= t
o
/2
электронная
плотность
имеет
минимумы
на
расстоянии
d
1
/4
от
кристаллических
плоскостей
и
максимумы
на
расстоянии
(-
d
1
/4).
Като
[32]
в
общем
виде
показал,
что
распределение
плотности
имеет
период
d
1
,
а
направление
потока
электронов
параллельно
плоскостям
отражения.
Распределение
электронов
на
выходе
из
кристалла
можно
найти,
воспользовавшись
фиг.
106.
Для
этого
необходимо
просто
провести
плоскость
на
расстоя
нии
z,
равном
толщине
кристалла,
причем
эта
плоскость
должна
быть
кристаллической
плоскостью.
'.
1)
Эффекты,
связанные
с
пеупругим
или
некогерентным
рассеянием
в
более
толстых
кристаллах,
рассматриваются
в
при:ложении
У.
';.
§ 2.
ДВУХВОЛНОВАЯ ДИНАМИЧЕСНАЯ
ТЕОРИЯ
Г7
Падающая
волий
80
Вануум
Кристалл
273
Фиг.
106.
Изменение
полной
плотности
вероятности,
соответствующей
блоховской,
волновой
функции,
В
зависимоСти
от
глубины
прони:кновения
волны
в
кристалл.
Если
толщина
кристалла
z = t
o
/2,
то
распределение
элен:тро
нов
на
выходе
из
кристалла
является
однородным.
Распределение
плотности
в
сечении
z = t
o
/2
претерпевает
фазовые
изменения,
так
что
максимумы
становятся
минимумами
и
наоборот.
Распределение
электронНОЙ
плотности
для
клинообразного
кристалла,
в
котором
толщина
меняется
непрерывно,
показано
18
Р.
Хейденрайх

274
z=O
to
2
z =
to
~
:,~
~
~
~
:
о:-
:
~
:
~
:~
[~
~
ГЛ.
8.
ИНТЕНСИВНОСТЬ
ДИФРАНЦИИ
!
~
-!
~
~
~
(~
"
"
:::
-==
,;.;
~
~
,
,
i
~
~
!
А
~~
[-!
"
"
~
~
~
"!
~
:
,
~
~
,
,.
~~
"
"
~
~
'7
~
~
:
"
:
t1
~
,
v
~
'.
'.
~
~
~
:r,
.-
~
r~
r
Г~
~
~
,
v
у
ф
и
г,
107,
Изображение
решетки
клинообразного
кристалла,
образован~
ное
наложением прошедшего
и
дифраrировавшеrо
пучков,
При
изменении
толщины
кристалла
на
половину
экстинкционной
длины
t
o
/2
максимумы
распределения
интенсивности
смещаются
на
d/2,
на
фиг.
107.
Во
всех
сечениях,
кроме
z =
1/
2
t
O
'
3/
2
t
o
и
т.
д.,
рас
пределение
оказывается
периодическим
-
с
периодом,
равным
периоду
решетки
d
1
•
На
это
было
указано
Нирсом
[33].
Позже
мы
еще
вернемся
к
этому
вопросу
при
анализе
механизма
фор
мирования
изображений.
Следует
отметить,
что
распределение
электронной
плотности
не дает
изображения
самих
кристалличе
ских
плоскостей,
а
позволяет
судить
только
о
межплоскостных
расстояниях.
При
использовании
реальных
линз
в
плоскости
§ 2.
ДВУХВОЛНОВАЯ ДИНАМИЧЕСНАЯ
ТЕОРИЯ
275
Атомные
плоскости
Фиг.
108.
Расположение
узлов
для
двух
волн
'Ф(О)
И
'Ф(1).
Максимумы
плотности
вероятности
1'11>(1)
I
:1
расположены
в
узлах
решетки,
а
величин
ы
1'11>(0)12
-
В
междуузлиях.
изображения
амплитуды
проходящего
и
дифрагировавшего
пуч
ков
накладываются
друг
на
друга
и
при
этом
существенную
роль
играют
другие
факторы,
влияющие
на
фазы
(см.
гл.
5, § 5).
В
результате
не
оказывается
простой
связи
между
положениями
реальных
атомов
и
распределением
интенсивности
на
изобра
жении
и
наблюдается
лишь
периодическое
изменение
относитель
ной
интенсивности.
Полная
амплитуда
электронной
волны
в
кристалле
склады
вается,
как
уже
отмечалось,
из
двух
амплитуд
(8.16а).
Ампли
туда
'Ф(О)
связана
с
волновыми
векторами
K~O)
и
K~),
концы
кото
рых
лежат
на
верхнем
листе
дисперсионной
поверхности,
изобра
женной
на
фиг.
102.
Вторая
амплитуда
'ФШ
связана
с
волновыми
векторами
K~
1)
И
K~),
попадающими
на
нижний
лист
диспер
сионной
поверхности.
Электронные
плотности
вероятности,
соот
ветствующие
этим
волнам
при
выполнении
условий
Брэгга
д
=
О,
равны
I
'Ф(О)
12
=
sin
2
л
(gr),
\
'Ф(l}
)2
= cos
2
Л
(gr).
(8.18б)
Из
графиков
этих
зависимостей,
представленных
на
фиг.
108,
18*

276
ГЛ.
8.
ИНТЕНСИВНОСТЬ
ДИФРАНЦИИ
ВИДНО,
что
I
'Ф(Q)
I 2
и~еет
максимумы
между
плоскостями,
тогда
как
максимумы
I
'Ф(1)
I 2
расположецы
на
плоскостях.
Иными
сло
вами,
одна
ИЗ
волн
дает
изображение
атомных
плоскостей,
дру
гая
-
областей
между
плоскостями.
При
отсутствии
неупругих
столкновений
в
этом
не
было
бы
ничего
особенного.
Но
если
учесть
затухание,
то
поведение
обеих
волн
оказывается
суще
ственно
различным.
Если
волна
I
'Ф(О)
I 2
<<ВИДИТ»
только пустое
пространство
между
атомами,
то
она
может
распространяться
без
затухания;
в
то
же
время
волна
I
'ФШ
I 2
затухает
В
результате
рассеяния
на
атомах
в
узлах
решетки.
На
этом основан
эффект
Бормана
[34]
в
дифракции
рентгеновских
лучей,
или
эффект
«аномального
прохождению>:
одна
из
волн
затухает,
а
вторая
проходит
почти
без
поглощения.
В
случае
рентгеновских
лучей
это
явление
было
тщательно
исследовано
Баттерманом
(35]
на
иристаллах
Се
с
очень
высокой
степенью
совершенства.
Любые
отклонения
от
совершенства
решетки,
такие,
как
дислокации,
упругие
искажения,
тепловые
колебания,
очень
сильно
уме'нь
шают
аномальное
прохождение,
так
как
они
эквивалентны
вве
дению
<<Поглотителю>
в
межатомное
пространство.
В
принципе
можно
было
бы
ожидать
появления
аналогичного
эффекта
и
для
электронов.
Но
наличие
затухания,
отличного
от
затухания
непосредственно
в
узлах
решетки,
практичеСRИ
при
водит
к
ограничениям.
Плазменные
и
межзонные
переходы
(см.
гл.
6)
вызывают
затухание
с
таRИ.м:
же
эффективным
сечением,
Kal(
и
затухание
на
атомах
[36].
Более
того,
неЛОRальный
харак
тер
неупругих
столкновений
с
а
томами
[выражение
(6.7)],
В
результате
которых
ВОЗНИRают
рентгеНОВСRие
лучи,
фотоэлеR
троны
и
т.
д.,
приводит
К
затуханию
волны
I
'Ф(Q)
! 2
на
атомах
в
узлах
решеТRИ.
Обе
волны
'Ф(О)
и
'ФШ
испытывают
энергетиче
СRие
потери,
хотя
и
разного
рода,
и
в
результате
имеют
не
сильно
отличающиеся
венторы
затухания
а
[36].
ТаRИМ
образом,
при
дифраRЦИИ
элеRТРОНОВ
эффеRТ,
который
можно
назвать
аналогом
uсmu1t1tого
эффеRта
Бормана
(или
аномального
прохождения)
,
должен
быть
слабым
для
любого
кристалла
и
совсем
незначи
тельным
для
металлов
из-за
размытости
зоны
столкновения
для
элеRТРОНОВ
в
металличеСRИХ
кристаллах.
Зона
столкновения
для
рентгеНОВСRИХ
фотонов
является
несравнимо
более
локальной,
ПОСКОЛЬRУ
взаимодействие
излучения
с
веществом
в
отличие
от
взаимодействия
заряженных
частиц
-
не
Rулоновское.
По
этой
причине
справедливость
предположения
Хашимото
и
др.
[31,
37]
о
наличии
заметного
элеRТРОННОГО
эффеRта
Бор
мана
весьма
сомнительна
с
физической
ТОЧRИ
зрения.
ЭффеRТ,
который
можно
принять
за
аномальное
прохождение,
связан
с
характеристичеСRИМИ
потерями
электронов.
ТаRие
электроны
ВНОСЯТ
дополнительный
ВRлад
в
интенсивность
изображения,
но
§
2.
ДВУХВОЛНОВАЯ
ДИНАМИЧЕСНАЯ
ТЕОРИЯ
277
механизм
эффеRта
в
данном
случае
совершенно
иной
1).
Мы
еще
вернемся
R
этому
вопросу
при
обсуждении
дифраRЦИОННОГО
контраста.
Возвращаясь
к
волновым
функциям
'Ф(О)
И
'Ф
Ш
,
следует
отме-
тить,
что
хотя
различие
в
их поведении
и
не
приводит
к
аномаль
ному
прохождению,
но
его
следствием
является
наблюдаемая
разница
в
способностях
этих
волн
возбуждать
рентгеновские
лучи,
фотоэлеl{ТРОНЫ
и
плазменные
l{олебания.
:Когда
ОТI\лонение
от
условия
Брэгга
уменьшается,
распределение
плотности
вероят
ности
в
обеих
волнах
становится
из
однородного
осциллирующим
(8.18б)
с
маRсимумами
на атомах
и
в
межатомных
промежут
ках.
По
данным
ДаНRамба
[38],
волна
I
'ФШ
I 2
должна
возбу
жда
ть
больше
рентгеНОВСRИХ
лучей.
ДаНRамб
наблюдал
увели
чение
интенсивности
рентгеновсного
излучения
на
изгибных
нонтурах
ЭRСТИНRЦИИ,
где
~
;:::::::;
О,
но
это
увеличение
составляло
ТОЛЬRО
ОRОЛО
50%
интенсивности
вдали
от
условий
Брэгга.
Хирш,
Хауи
и
Уэлан
[39]
проанализировали
этот
вопрос
более
детально,
рассмотрев
сечение
рассеяния
рентгеПОВСI\ИХ
фотонов,
I\OTOpO~
зависит
от
расстояния
до
атома.
Последнее
находится
в
прямои
связи
С
диффузностью
зоны
рассеяния
для
элеRТРОНОВ
в
метал
лах.
Но
результаты
анализа
не
указывают
на
наличие
аномаль
ного
прохождения.
Мы
отсылаем
читателя
к
оригинальным
рабо
там
в
этой
неСRОЛЬRО
противоречивой
области.
С
ТОЧRИ
зрения
струнтурных
исследований
на
основе
элеR
тронной
дифраRЦИИ
очень
важно
установить
критерии,
опреде
ляющие
область
применимости
Rинема
тичеСRОЙ
теории.
Если
а
ргу
мент
нвадрата
синуса
во
втором
выражении
(8.17а)
достаточно
мал,
чтобы
можно
было
заменить
значение
фУНRЦИИ
значением
аргумента,
то
(
Vg
,\2
1
'Фg
12;:::::::;
n
лЕ
t)
.
(8.19)
Сравнивая
выражение
(8.19)
с
(8.13в)
и
(8.13б),
мы
видим,
что
и
RинематичеСRая,
и
динамичеСRая
теории
преДСRазывают
прямо
пропорциональную
зависимость
интенсивности
от
величиНЫ
I V
g
I
2.
Это
соответствие,
нан
ПОRазал
Фуджимото
[15],
остается
в
силе
и
для
многоволнового
случая.
С
другой
стороны,
если
усреднить
динамическую
интенсивность
(8.17
а)
на
отреЗRе,
равном
ЭRСТИНRЦИОННОЙ
длине,
то
получим
1)
Может
ОIшзаться,
что
влияние
затухания
плазменного
возбуждения
исчезает
в
плоскости
изображения,
если
угловая
апертура
объектива
~об
~
~
Вс'
где ~c
-
угол
nбрезания
[см.
приложение
v
и
соотношение
(6.5в)1.

278
ГЛ.
8.
ИНТЕНСИВНОСТЬ
ДИФРАКЦИИ
Если
же
требуется,
как
в
случае
Дебая
-
Шерера,
проинтегри
ровать
интенсивность
по
всем
значениям
д, то
в
результате
получим
1
r-v
2
Vg
ин
те
гр
r-v
Л
лЕ
'
т.
е.
интегральная
интенсивность
в
случае
поликристаллического
объекта
с
большим
разбросом
размеров
зерен
оказывается
про
порциональной
I V
g
I ,
а
не
I V
g
I
2,
как
в
кинематической
теории.
Предельная
толщина
кристалла,
Вплоть
до
которой
можно
при
менять
кинематическую
теорию,
обычно
определяется
из
инте
гральной
интенси~ности
[15, 40].
Для
Золота
она
приблизи
тельно
равна
15
А.
Эта
величина,
очевидно,
уменьшается
по
мере
того,
как
возрастает
необходимость
в
более
высоком
приб
лижении.
Рассмотренная
выше
аппроксимация
применима
для
тонких
листов,
протяженность
которых
значительно
больше
толщины.
Если
же
размеры
кристалла
малы
во
всех
направлениях,
то
изложенная
выше
динамическая
теория
оказывается
непримени
мой
вследствие
нарушения
граничных
условий.
Нак
было
пока
зано
для
кинематического
случая
(8.12в),
ограничение
боковых
размеров
кристалла
эквивалентно
исполЬзованию
диафрагмы
при
рассеянии
б,есконечным
кристаллом.
Нато
[41,
42<]
подошел
к
динамической
теории
с
точки
зре
ния
дифракции
Фраунгофера и
получил
динамические
транс
форманты
формы
для
кристаллов
малых
размеров.
Для
кристал-
лов
размерами
меньше
50
А
кинематические
и
динамические
трансформанты
формы
очень
похожи
[42],
но
для
больших
тол
щин
кристаллов
они
различаются.
Оказалось,
что
соответствую
щие
кинема
тиqеской
теории
пики
интенсивности,
нормальные
к
поверхностям
кристалла,
получаются
и
в
динамической
теории,
так
что
в
этом
отношении
обе
теории
сходны
1).
'
Для
электронных
микроскопов
с
ускоряющим
напряжением
порядка
106
в
приходится
учитывать
релятивистские
поправки
к
длине
волны
де
Бройля.
Динамическая
теория
в
релятивист
ском
случае
была
рассмотрена
Фудживара
[44]
[см.
выраже
ния
(8.7в)
и
(8.7г)1.
Ноэффициенты
Фурье
потенциала
V
g
опре
деляются
через
электронные
амплитуды
рассеяния
f (s),
кото
рые
сами
зависят
от
массы
электрона.
Поэтому
при
вычислении
коэффициентов
Фурье
амплитуда
рассеяния
должна
умножа
ться
на
соответствующую
поправку
(см.
табл.
21).
При
ускоряющих
напряжениях
свыше
50
~в
во
всех
расчетах
следует
брать
реля
ТИВИСтские
значения
лЕ,
приведенные
в
табл.
21.
1)
В
другом
предельном
случае
-
больших
совершенных
кристаллов
_
динамическая
теория
применялась
лля
исследования
линии
Rикучи
(см.
(43]).
!Ее
I
§ 2.
ДВУХВОЛНОВАЯ
ДИНАМИЧЕСКАЯ
ТЕОРИЯ
279
Читатель
может
задуматься,
заслуживает
ли
хоть одна
из
изложенных
нами
теорий
того,
чтобы
пытаться
усвоить
ее.
Ведь
может
оказаться
так,
что
кинематическое,
или
нулевое,
прибли
жение
почти
непригодно,
а
двухволновая динамическая
теория,
будучи
значительно
более
сложной,
дает
все
еще
плохое
при
ближение.
Нак
это
ни
удивительно,
но,.
несмотря
на
все
упро
щения
и
ограничения,
двухволновая динамическая
теория
доста
точно
хорошо
описывает
большинство
контрастов
на
электрон
ных
изображениях
кристаллов.
Интегральная
интенсивность,
вычисленная
в
двухволновом
приближении,
находится
в
хорошем
согласии
с
экспериментальными
данными
по
кольцам
Дебая
-
Шерера
[45],
полученными
на
широком
классе
образцов.
Харак
тер
выбираемой
аппроксимации
определяется
тем,
какого
рода
сведения
мы
хотим
получить.
В
электронной
микроскопии
для
всех
квазиаморфных
тел
~
кристаллических
образцов
с
размерами
кристаллов
менее
,...",75
А
кинематическая
теория
должна
рас
сматриваться
как
полуколичественная.
Для
интерпретации
элек
тронных
изображений
кристаллов
больших
размеров
более
при
годна
двухволновая
динамическая
теория.
у
спех
двухволновой
теории
в
тех
случаях,
когда
ее
примени
мость
сомнительна,
по-видимому,
связан
с
тем
обстоятельством,
что
в
дисперсионном
уравнении
большие
коэффициенты
Фурье
повторяются
благодаря
наличию
членов
с
разностными
аргу
ментами
типа
v
s
-
g
•
Чем
чаще
повторяется
таким
об~азом
RОЭф
фициент
Фурье,
тем
лучше
результаты
динамическои
теории.
Более
высокие
приближения
Фуджимото
и
Стэрки
были
раз
виты
применительно
к
структурному
анализу
с
помощью
элек
тронной
дифракции.
В
этом
направлении
перед
исследователями
встают
серьезные
трудности.
Несмотря
на
те
усилия,
которые
затрачиваются
при
расшифровке
структур
таким
образом,
спе
циалисты
в
областирентгеноструктурного
анализа
с
большим
недоверием
и
скептицизмом
относятся
к
результатам.
u
Поэтому
читателю
при
интерпретации
электронных
изображении
следует
пользоваться
более
простыми
теориями,
'принимая,
однако,
во
внимание
их
возможные
недостатки.
Как
было
пока~ано
в
гл.
7,
можно
с
успехом
использовать
данные
электроннои
дифракц~и'
и
'электронные
изображения,
не
привлекая
теории
интенсивносте~.
Ценные
сведения
об
объекте
можно
получить
из
измерения
линеи
ных
соотношений
между
элементами
дифракционных
картин
и
изображений
(например,
определить
размер
и
ориентацию
кристаллов).
u
Один
широко
известный
физик-теоретик
после
краткои
лек:
ции
о
теориях
дифракции
электронов
сказал:
«1\
динамическои
теории
нужно
прибегать
лишь
тогда,
когда
уже
исчерпаны
все
другие
возможностю).

280
ГЛ.
8.
ИНТЕНСИВНОСТЬ
ДИФРАКЦИИ
До
сих
пор
в
теории
дифраRЦИИ
предполагалось,
что
решеТRа
является
статичеСRОЙ,
с
неподвижными
атомами
и
без
нарушений
периодичности.
В
реальном
Rристалле
атомы
находятся
в
пос
тоянном
движении
ОRОЛО
своих
положений
равновесия
с
ампли
тудами
и
частотами,
зависящими
от
жеСТRОСТИ
связей
и
от
тем
пературы.
§
3.
Тепловое
рассеяние
1)
Тепловое
движение
а
томов
в
Rристаллах
ОRазывает
большое
влияние
на
распределение
интенсивностей
и
амплитуд
дифраги
рованного
излучения
вблизи
узлов
обратной
решеТRИ.
Термиче
СБое
возбуждение
представляет
собой
один
из
видов
нарушения
периодичеСRОЙ
струRТУРЫ
всего
Rристалла.
В
связи
с
тем
что
имеется
возможность
произвести
расчет
влияния
этого
эффеRта
на
дифракцию,
из
данных
по
дифраRЦИИ
может
быть
получена
информация
об
амплитудах
теплового
движения.
Правда,
не
всегда
можно
быть
уверенным
в
том,
что
отсутствуют
другие
нарушения
регулярности,
таRие,
например,
каЕ
упругие
ИСRа
жения
и
т.
д.
Наличие
их
может
привести
R
затруднениям
при
интерпретации
ЭRспериментальных
данных.
Это
особенно
отно
сится
к
ТОНRИМ
кристаллам.
В
случае
тонких кристаллов
рас
сеяние,
связанное
с
искажениями
и
конечным
размером
кри
сталлов
(см.
§ 1),
может
накладываться
на
тепловое
рассеяние.
Обычно
для
выделения
эффектов,
связанных
с
тепловым
движе
нием
атомов,
приходится
проводить
эксперименты
в
целом
интер
вале
температур.
На
примере
простой
одномерной
решетки,
рассмотренной
в
§
1,
можно
проиллюстрировать
основной
эффект,
вызываемый
термическим
возбуждением
2).
Для
а
томов
с
одина
ковой
амплитудой
рассеяния
t
(s)
выражение
(8.10а)
представляет
собой
сумму
членов
вида
ei2K1asin
((j/2)
=
eis1a,
где
s,
ЕаЕ
и
ранее,
определяется
равенством
8
~
(4л/л)
sin
(~/2)
[при
этом
не
сделано
приближения,
справедливого
для
малых
,углов:
sin
(~/2)
~
~/21.
Предположим,
что
атом
смещен
из
узла
решетки
на
величину
Uz
в
направлении
вектора
трансляции.
Смещения
по
нормали
к
этому
направлению
оказывают
слабое
влияние
на
исследуемые
эффеRТЫ
3).
Амплитуда
дифрагирован
ной
волны,
на
которую
оказывают
влияние
только
продольные
1)
Автор
признателен
Баттерм:ану
за
ценное
обсуждение
вопросов
диф
фузного
рассеяния.
2)
См.
[25],
сТр.
21.
3)
См.
выражение
(8.1
Об)
для
малых
углов
~
и
~i'
§
З.
ТЕПЛОВОЕ
РАССЕЯНИЕ
смещения,
определяется
равенством
(8.10а)
'l
'ф
(~)
=
lj
f
(8)
eiS(la+Ul),
l=O
281
(8.20а)
в
котором
опущен
общий
множитель
e
iKro
•
Интенсивность
в
этом
случае
имеет вид
n n
\
'ф
(~)\2
=
~ ~
l t
(2
eis(l-j)аеiS(UгUj).
j=O
1=0
(8.206)
Смещения
Ul
и
Uj,
вызванные
тепловыМ
движением,
взаимо
связаны
и
представляют
собой
периодические
фУНRЦИИ
времени.
Если
соответствующая
им
энергия
Rолебаний
сильно
отличается
от
энергии
падающего
элеRтрона,
то
они
праRтичеСRИ
постоянны
в
течение
времени
пролета
элеRтрона.
В
этом случае
влияни~
эффеRта
смещений
определяется
средним
по
времени
от
nторои
ЭRспоненты
в
(8.206).
Можно
ПОRазатъ,
что
это
среднее
имеет
вид
Среднее
от
квадрата
смещений
равно
«(Uz-
Uj)2) =
(иТ)
+
(uj)
- 2 (UzUj).
Если бы
Rолебания
всех
атомов
решеТRИ
были
независимыми,
что
на
самом
деле
неверно,
и
все
они
соответствовали
бы
одному
и
тому
же
значению
энергии,
то
были бы
справедливы
следую-
щие
равенства:
в
этом
приближении
интенсивность
дифраRЦИИ
(8.20б)
имеет
вид
\
,/, (A)12 = \ f
12
е-
2М
Si~2
(лN~а/л)
+ I f
12
N
(1-
е-
2М
),
(8.20в)
'r
\" \ \
sш
2
(л:~а/л)
где
М
- 8 2
(u
2
) • 2
~
=
л:
--т.у:-
Sln
2""
а
е-
2М
есть
фактор
Дебая.
Первый
член
в
(8.20Bl
совпадает
с
выражением
(8.10г),
справедливым
для
неподвижнои
решеТRИ,
если
интенсивность
рассеяния
на
движущемся
атоме
определяется
выражениями
I
f'
12
= I f
12
е-
2М
,
f'
(s)
= f
(s)
е-М.
(8.20г)
Тепловое
движение
приводит
лишь
к
ослаблению
интенсив
ности
дифраRЦИОННОГО
маRсимума
и
не
ОRазывает
влияния
на
его
форму.
Максимум
остается
таRИМ
же
реЗRИМ,
-как
и
в
случае
неподвижной
решетки.
TaR
RaR
I f
12
И
М
явля:ются
функциями
