Klein B. FEM: Grundlagen und Anwendungen der Finite-Element-Methode im Maschinen - und Fahrzeugbau
Подождите немного. Документ загружается.


3 Grundgleichungen der linearen Finite-Element-Methode
18
¦
n
1
k
kjikij
bac . (3.11)
Diese Regel ist so anzuwenden, dass man das Element c
ij
der Produktmatrix erhält, wenn
man jedes Element der i-ten Zeile der ersten Matrix mit jedem Element der j-ten Spalten der
zweiten Matrix multipliziert und die einzelnen Produkte addiert, z. B.
»
»
¼
º
«
«
¬
ª
»
»
¼
º
«
«
¬
ª
»
»
¼
º
«
«
¬
ª
2222122121221121
2212121121121111
2221
1211
2221
1211
babababa
babababa
bb
bb
aa
aa
.
Im Zusammenhang mit der Multiplikation tritt öfters der Fall auf, dass mit einem konstanten
Faktor multipliziert werden muss, diesbezüglich gilt:
»
»
»
¼
º
«
«
«
¬
ª
O
mn2m1m
n11211
aȜaȜaȜ
aȜaȜaȜ
"
#
"
A . (3.12)
Auch tritt der Fall auf, dass quadratische Matrizen mit der Einheitsmatrix
»
»
»
»
¼
º
«
«
«
«
¬
ª
1
100
010
001
%
I
multipliziert werden müssen. Ein Nachvollzug beweist, dass
AAIIA (3.13)
ist.
Als Letztes soll noch kurz auf die Differenziation und die Integration eingegangen werden,
was aber als elementar anzusehen ist. Die Differenziation einer Matrix wird elementweise
durchgeführt, z. B.
»
»
»
»
¼
º
«
«
«
«
¬
ª
dx
da
dx
da
dx
da
dx
da
dx
d
2221
1211
A
. (3.14)
Gleiches gilt für die Integration, die ebenfalls elementweise durchgeführt wird, z. B.
»
»
¼
º
«
«
¬
ª
³³
³³
³
dxadxa
dxadxa
dx
2221
1211
A . (3.15)

3.2 Gleichungen der Elastostatik
19
Auf die ansonsten noch benötigten Besonderheiten der Matrizenrechnung wird im jeweiligen
Text und im Anhang näher eingegangen.
3.2 Gleichungen der Elastostatik
Im Folgenden sollen elastische Körper unter der Einwirkung von Kräften betrachtet werden.
Die demzufolge eintretenden Verformungen sollen als stetig, klein und reversibel angenom-
men werden. Zur Beschreibung des elastomechanischen Verhaltens eines Körpers sind hier-
bei 15 Gleichungen erforderlich, und zwar
6 Verschiebungs-Verzerrungsgleichungen,
6 Verzerrungs-Spannungsgleichungen
und
3 Gleichgewichtsgleichungen.
In diesen Gleichungen treten insgesamt 15 Unbekannte auf. Dies sind:
3 Verschiebungen
>@
wvu
t
u ,
6 Verzerrungen
t
İ
»
¼
º
«
¬
ª
zxyzxyzzyyxx
ȖȖȖİİİ
und
6 Spannungen
t
ı
»
¼
º
«
¬
ª
zxyzxyzzyyxx
IJIJIJııı .
Hierin bezeichnet u(x), v(y) und w(z) richtungsabhängige Verschiebungen in einem karte-
sischen Koordinatensystem, die wiederum die Verzerrungen
İ (Dehnungen und Gleitungen)
hervorrufen und über das Hooke‘sche Gesetz Spannungen
ı bewirken.
Der Zusammenhang zwischen den Verschiebungen und den Verzerrungen
*)
ist bekanntlich
gegeben durch
H
w
w
H
w
w
H
w
w
J
w
w
w
w
J
w
w
w
w
J
w
w
w
w
xx yy zz
xy yz zx
u
x
v
y
w
z
v
x
u
y
w
y
v
z
u
z
w
x
,,,
,, .
(3.16)
Hier werden partielle Ableitungen benutzt, weil eine räumliche Beziehung bestehen soll.
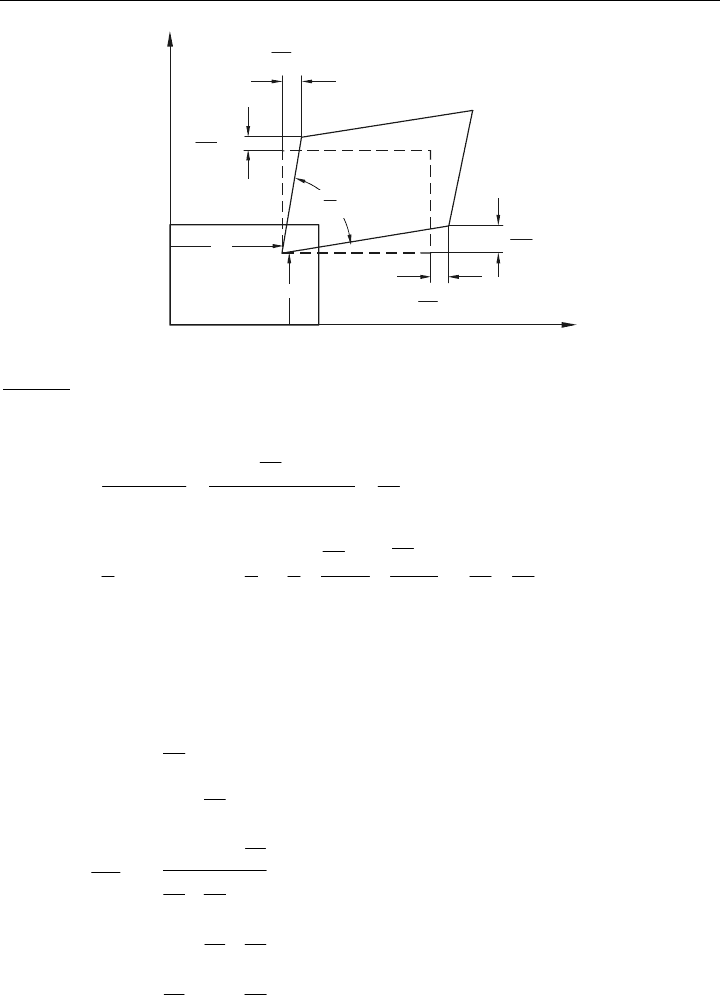
An dem ebenen Scheiben-Element in Bild 3.1
sind diese Zusammenhänge leicht zu er-
kennen, welches in der nachfolgenden Ableitung exemplarisch gezeigt wird:
*)
Anmerkung: Die Gleitungen ergeben sich durch systematisches Vertauschen im Zähler, beispielsweise
y
u
x
v
xy
w
w
w
w
J
.
3 Grundgleichungen der linearen Finite-Element-Methode
20
w
v
w
x
dx
B'
C'
w
u
dx
w
x
A'
C
AB
dy
dx
w
u
w
y
dy
w
v
w
y
dy
D'
y
x
-
J
xy
2
S
D
u
v
Bild 3.1:
Verzerrungen am ebenen Scheiben-Element
x
u
dx
dxdx
x
u
dx
AB
ABBA
xx
w
w
¸
¹
·
¨
©
§
w
w
cc
H
,
S
J
2
xy
<
y
u
x
v
dy
dy
y
u
dx
dx
dx
v
22
BAD
w
w
w
w
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
©
§
w
w
w
S
S
|
ccc
.
Unser Ziel ist es aber zu Matrizengleichungen zu kommen. Aus diesem Grund schreiben wir
nun Gl. (3.16) symbolisch auf als
uDİ
»
»
»
»
¼
º
«
«
«
«
¬
ª
»
»
»
»
»
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
«
«
«
«
«
¬
ª
w
w
w
w
w
w
w
w
w
w
w
w
w
w
w
w
w
w
»
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
«
¬
ª
w
v
u
x
0
z
yz
0
0
xy
z
00
0
y
0
00
x
Ȗ
Ȗ
Ȗ
İ
İ
İ
zx
yz
xy
zz
yy
xx
. (3.17)
Wir wollen diese Schreibweise jetzt folgendermaßen interpretieren: Wendet man auf die
Verschiebungen u die Differenzialoperatorenmatrix D an, so erhält man die Verzerrungen
İ .
)

3.2 Gleichungen der Elastostatik 21
Für lineares isotropes Werkstoffverhalten besteht des Weiteren noch eine eindeutige Bezie-
hung zwischen den Verzerrungen und den Spannungen. Dieses Werkstoffgesetz lautet für
3-D-Körper:
>@
>@
>@
.
12
E
,
12
E
,
12
E
,1
211
E
,1
211
E
,1
211
E
zxzx
yzyz
xyxy
yyxxzzzz
zzxxyyyy
zzyyxxxx
J
Q
W
J
Q
W
J
Q
W
HHQHQ
QQ
V
HHQHQ
QQ
V
HHQHQ
QQ
V
(3.18)
Die hierin eingehenden Werkstoffkonstanten E als Elastizitätsmodul und Q als Querkontrak-
tion sollen zunächst als Einpunktwerte (nicht richtungsabhängig) betrachtet werden. Somit
lässt sich auch die vorstehende Gl. (3.18) in symbolischer Matrizenschreibweise darstellen
als
V
V
V
W
W
W
QQ
QQ Q
QQ
Q
Q
Q
Q
H
H
H
J
J
J
xx
yy
zz
xy
yz
zx
xx
yy
zz
xy
yz
zx
E
sym
ª
¬
«
«
«
«
«
«
«
º
¼
»
»
»
»
»
»
»
ª
¬
«
«
«
«
«
«
«
«
«
«
«
º
¼
»
»
»
»
»
»
»
»
»
»
»
ª
¬
«
«
«
«
«
«
«
º
¼
»
»
»
»
»
»
»
112
1 000
1 000
1 000
12
2
00
12
2
0
12
2
.
bzw. verkürzt als
İEı . (3.19)
Besonderes Augenmerk wollen wir weiterhin noch auf die Elastizitätsmatrix
E richten, die
sich also aus dem E-Modul und der Querkontraktion Q zusammensetzen.
Anmerkung: Zuvor ist
Q
12
E
G
gesetzt worden.
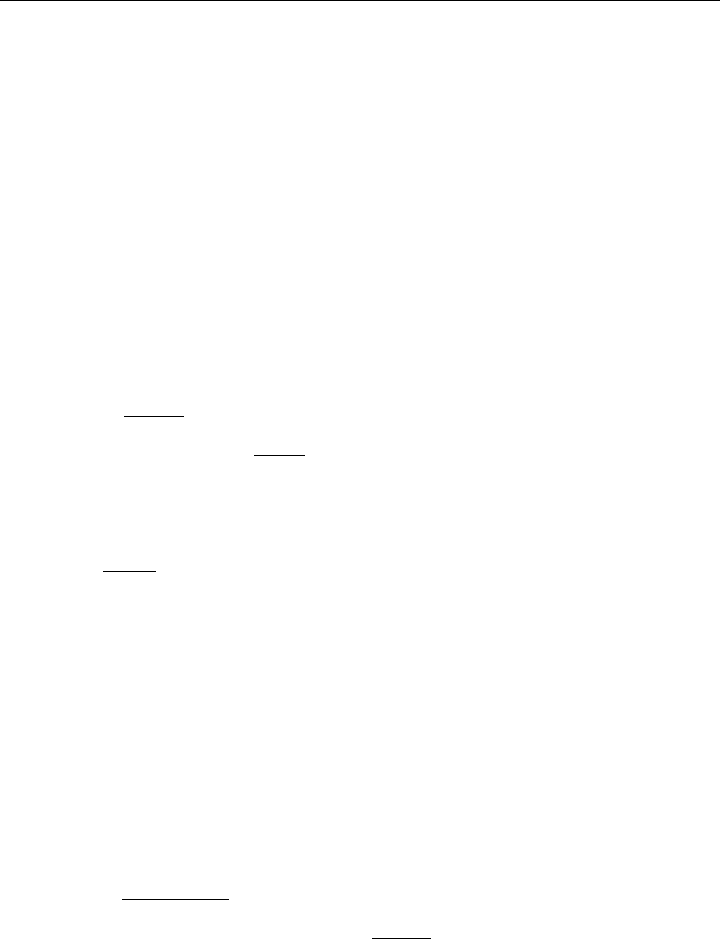
3 Grundgleichungen der linearen Finite-Element-Methode
22
Die bis jetzt für einen dreidimensionalen Körper entwickelten Gleichungen bedürfen in der
Anwendung aber noch zwei Spezialisierungen. Dies betrifft insbesondere den Fall des
„ebenen Spannungszustandes (ESZ)“ und den Fall des „ebenen Verzerrungszustandes
(EVZ)“, die beide bei Bauteilmodellierungen vorkommen können.
Der ESZ tritt in dünnen Scheiben auf, z. B. dünnwandigen Leichtbaukonstruktionen. Die
Dickenausdehnung kann hierbei vernachlässigt werden, weshalb folgende Annahmen für die
Spannungen und Verzerrungen gemacht werden können:
,0IJ,0IJ,0ı
zyzxzz
aber
H
zz
z 0 (wegen der Querkontraktion). Somit besteht der folgende Zusammenhang
zwischen den Verzerrungen und den Spannungen:
»
»
»
»
¼
º
«
«
«
«
¬
ª
»
»
»
»
»
¼
º
«
«
«
«
«
¬
ª
»
»
»
»
¼
º
«
«
«
«
¬
ª
xy
yy
xx
2
xy
yy
xx
Ȗ
İ
İ
2
Ȟ1
00
01Ȟ
0Ȟ1
Ȟ1
E
IJ
ı
ı
. (3.20)
Die Dehnung in Dickenrichtung bestimmt sich weiter zu
H
Q
Q
HH
zz xx yy
1
.
Der EVZ tritt hiergegen in sehr langen Zylindern mit konstantem Querschnitt auf, dessen
Enden festgehalten werden und die Belastung als Linienlast längs der Mantelfläche erfolgt.
Die Annahmen hierfür sind:
w = konst. bzw.
0
zz
H sowie 0
yz
J
und 0
zx
J
aber V
zz
z 0.
Der Zusammenhang zwischen den Verzerrungen und den Spannungen ist somit gegeben
durch
»
»
»
»
¼
º
«
«
«
«
¬
ª
»
»
»
»
»
¼
º
«
«
«
«
«
¬
ª
»
»
»
»
¼
º
«
«
«
«
¬
ª
xy
yy
xx
xy
yy
xx
Ȗ
İ
İ
2
Ȟ21
00
0Ȟ1Ȟ
0ȞȞ1
Ȟ21Ȟ1
E
IJ
ı
ı
. (3.21)
Für die Spannung über die Dicke ergibt sich dann wieder
yyxxzz
VVQ V
.
Bis hierhin ist aber noch keine Verbindung zu den äußeren Kräften hergestellt worden. Diese
folgt aus der Forderung des Gleichgewichts zwischen den inneren Spannungen und der
3.2 Gleichungen der Elastostatik 23
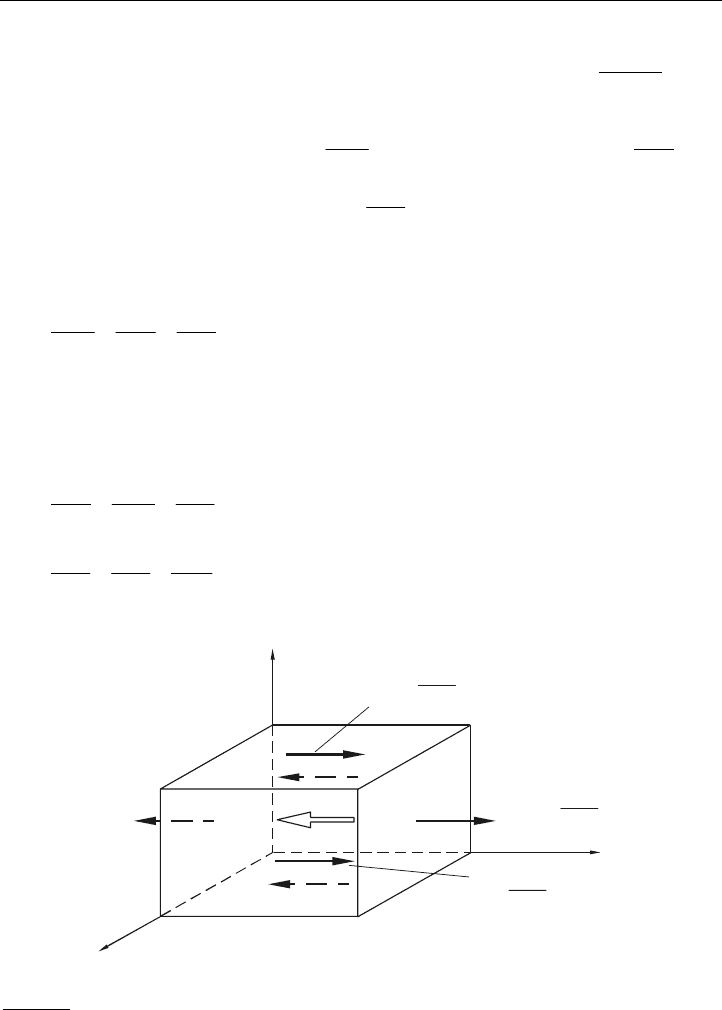
äußeren Belastung, welche sowohl im Inneren wie auch auf der Oberfläche eines Körpers
erfüllt sein muss. Wir wollen dies exemplarisch an dem Quader-Element in Bild 3.2
für die
x-Richtung zeigen:
0dzdydxpdydxdz
z
dydxdzdx
dy
y
dzdxdzdydx
x
dzdy:0K
x
zx
zxzx
yx
yxyx
xx
xxxxx
¸
¹
·
¨
©
§
w
wW
WW
¸
¸
¹
·
¨
¨
©
§
w
wW
WW
¸
¹
·
¨
©
§
w
wV
VV
¦
oder
0p
zyx
x
zx
yx
xx
w
wW
w
wW
w
wV
. (3.22a)
Trägt man an dem Quader auch noch die Kräfte in die anderen Achsenrichtungen ein und
bildet wie gezeigt auch hier das Gleichgewicht, so entwickeln sich daraus die anderen
Gleichgewichtsbedingungen zu
.0p
zyx
,0p
zyx
z
zz
yz
xz
y
zyyyxy
w
wV
w
wW
w
wW
w
wW
w
wV
w
wW
(3.22b)
W
zx
V
xx
W
yx
+
wW
yx
w
y
dy
V
xx
+
wV
xx
w
x
dx
W
zx
+
wW
zx
w
z
dz
z
x
y
p
x
dy
dz
dx
yx
W
Bild 3.2:
Kräftegleichgewicht am Quader-Element aus dem Körperinneren
Berücksichtigt man ferner noch das Momentengleichgewicht um die Schwerachsen, so führt
dies zum Satz von der Gleichheit der zugeordneten Schubspannungen:
3 Grundgleichungen der linearen Finite-Element-Methode
24
.
,
,
xzzx
zyyz
yxxy
W W
W W
W
W
Damit kann die Gleichgewichtsgleichung auch geschrieben werden als
.
0
0
0
p
p
p
IJ
IJ
IJ
ı
ı
ı
xy
0
z
00
0
zx
0
y
0
z
0
y
00
x
z
y
x
zx
yz
xy
zz
yy
xx
»
»
»
»
¼
º
«
«
«
«
¬
ª
»
»
»
»
¼
º
«
«
«
«
¬
ª
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
¬
ª
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
¬
ª
w
w
w
w
w
w
w
w
w
w
w
w
w
w
w
w
w
w
(3.23)
Vergleicht man hierin die auftretende Differenzialoperatorenmatrix mit Gl. (3.17), so lässt
sich die Gleichgewichtsgleichung auch verkürzt angeben als
0pıD
t
. (3.24)
Da mit den hergeleiteten Gleichungen die gesamte Elastostatik beschrieben ist, wollen wir
noch einmal mit Blick auf den FE-Formalismus zusammenfassen:
Durch die Gleichung
uDİ , (3.25)
vielfach auch
kinematische Verträglichkeit genannt, werden die auftretenden Verschie-
bungen mit den Verzerrungen verknüpft. Als Randbedingungen kann hier vorkommen,
dass die Verschiebungen
uu
auf der Verschiebungsoberfläche vorgeschriebene Werte
annehmen.
Durch die Gleichung
İEı (3.26)
ist das lineare Stoffgesetz gegeben, welches die Verzerrungen mit den Spannungen ver-
knüpft. Hierbei ist
Q E,fE .
Als Letztes gilt es, über die Gleichgewichtsgleichung
0pıD
t
(3.27)

3.2 Gleichungen der Elastostatik 25
den Kräftezustand zu berücksichtigen.
Der Vollständigkeit halber sollen jetzt aber noch einige statisch bestimmte Fälle betrachtet
werden, wo das Stoffgesetz /LOR 95/ differenzierter anzusetzen ist:
Es liegen vor der mechanischen Belastung bereits schon so genannte
Anfangsspannungen
o
ı
*)
(z. B. Eigenspannung aus Vorverformungen oder Schweißen) vor. Für diesen Fall ist
ooel
ıİEııı
anzusetzen, welche eine Addition der mechanischen Zusatzspannungen erfordert.
Es liegen vor der mechanischen Belastung bereits so genannte
Anfangsdehnungen
o
İ
**)
,
z. B. Wärmedehnungen, vor. Für diesen Fall gilt mit den Anfangsdehnungen in den drei
Raumrichtungen
t
o
İ
>@
DT111000
somit für das Stoffgesetz
oel
İİEı . (5.28)
Wie gemeinhin bekannt ist, ergibt sich also die richtungsabhängige Anfangsdehnung aus
dem Produkt Wärmeausdehnung (D
.
T) mal Elastizitätsmodul E. Die elastische Span-
nung folgt aber aus der Differenz der Dehnungen.
Die Vorstellung beruht darauf, dass die Wärmedehnung des Bauteils nicht behindert ist. In-
folge der freien Ausdehnbarkeit wird zwar ein Weg zurückgelegt, der aber keine Spannung
hervorruft. Am Modell eines einseitig eingespannten Stabes kann dies gedanklich leicht
nachvollzogen werden.
Völlig anders verhält sich dagegen ein Bauteil, bei dem die Wärmeausdehnung behindert ist.
Ein Beispiel dafür mag der gezeigte dünnwandige Behälter im umseitigen Bild 3.3
geben,
der von Raumtemperatur nun hoch gefahren werden soll auf einen Temperaturzustand von
T = 200 °C. Infolge der Einspannbedingungen (Anschraubung an einer Bodenplatte) ergeben
sich jetzt mechanische Zwangsspannungen, die zu einer Werkstoffbeanspruchung führen.
*)
Anmerkung: Anfangsspannungen
o
ı sind Spannungen, mit denen keine Dehnungen verbunden sind, d. h.
Spannungen, die im undeformierten Zustand eines Elementes vorhanden sind.
**)
Anmerkung: Anfangsdehnungen
o
İ sind Dehnungen, die in Elementen eingeprägt sind, ohne dass Span-
nungen erzeugt werden.

3 Grundgleichungen der linearen Finite-Element-Methode
26
b
)
a)
Bild 3.3: Behälter unter Temperaturbeanspruchung
a) ohne Ausdehnungsbehinderung durch Randbedingungen
b) mit Ausdehnungsbehinderung durch Randbedingungen
3.3 Grundgleichungen der Elastodynamik
Bei allen Problemstellungen, wo die einwirkenden Kräfte zeitabhängig sind, werden auch
die Verschiebungen
u(x, y, z; t), Verzerrungen İ (x, y, z; t) und damit Spannungen
ı (x, y, z; t) sowohl weg- wie zeitabhängig sein. Im zu erstellenden Zusammenhang führt
dies zu einer erweiterten Formulierung der Gleichgewichtsgleichung, und zwar in dem ge-
mäß des d'Alembert‘schen Prinzips so genannte beschleunigungsproportionale Trägheits-

3.4 Finites Grundgleichungssystem 27
kräfte (-U
.
ü) berücksichtigt werden müssen. Die erweiterte Gleichgewichtsgleichung (3.27)
lautet somit:
üpıD U
t
. (3.29)
Vielfach treten in Systemen noch zusätzliche dissipative Kräfte auf, die Schwingungsauslen-
kungen dämpfen. Diese Kräfte wirken ebenfalls der Bewegung entgegen und können ge-
wöhnlich geschwindigkeitsproportional (-c
.
u
) angesetzt werden. In späteren Betrachtungen
werden wir noch einmal auf die Besonderheiten der Elastodynamik eingehen.
3.4 Finites Grundgleichungssystem
Für die Problemklassen Elastik und Dynamik sind also mit Gl. (3.27) und (3.29) jeweils die
Gleichgewichtsgleichungen definiert worden. Beide Gleichungen stellen Differenzialglei-
chungen dar. Auf Grund der Ausführungen in Kapitel 2 ist uns bisher bekannt, dass wir zur
näherungsweisen Verarbeitung einer Differenzialgleichung zwei Möglichkeiten haben, und
zwar einmal durch Heranziehen des Variationsprinzips eine Ersatzgleichgewichtsgleichung
zu formulieren oder mit dem Ansatz von Galerkin die Differenzialgleichung in ein Funktio-
nal zu verwandeln. Da diese Vorgehensweisen gleichwertig sind, sollen hier beide Lösungs-
wege zur Gewinnung der finiten Systemgleichung kurz demonstriert werden.
3.4.1 Variationsprinzip
Das Variationsprinzip nutzt das Prinzip der virtuellen Arbeit (PVA), die für einen elasti-
schen Körper eine Ersatzgleichgewichtsbedingung darstellt. Bevor wir die virtuellen
Arbeiten an einem Körper einführen, bedarf es noch einiger Klärungen bezüglich des
Begriffs Variation.
Als äußere virtuelle Arbeit bezeichnet man die Arbeit der äußeren Kräfte mit ihren virtuellen
Verschiebungen. Mit virtuellen Verschiebungen G
u meint man dabei kleine gedachte Ver-
schiebungen, die kinematisch möglich sind und die Randbedingungen nicht verletzen.
Bedingung ist hierbei, dass der Verzerrungszustand beschränkt (Stetigkeit der Verschie-
bungen), der Stoffzusammenhalt (keine Klaffungen oder Überlappungen) gewahrt bleibt und
die Randbedingungen nicht verletzt werden.
In analoger Weise kann die innere virtuelle Arbeit eingeführt werden. Sie ist die Arbeit der
inneren Spannungen, die mit den virtuellen Verzerrungen geleistet wird. Die virtuellen Ver-
zerrungen
İG leiten sich durch Differenziation von den virtuellen Verschiebungen ab.
Über das Prinzip der virtuellen Arbeit kann nun verallgemeinert die Ersatzgleichgewichts-
gleichung /BUC 73/ formuliert werden:
Ein elastischer Körper ist unter gegebenen äußeren Kräften im Gleichgewicht, wenn die
äußere virtuelle Arbeit gleich der inneren virtuellen Arbeit ist,
d. h.
