Миронов С.В., Пищухин А.М. Метасистемный подход в управлении

Подождите немного. Документ загружается.

241

};Ni|v{VV

|V|i

∈

∪=

∈

(Г.15)

|S|k

Nk|s{SS

∈

∪=

∈

; (Г.16)

Понятно, что

V ⊆ и SV

⊆ для всех

∈

(Г.17)

Для нейтрального варианта SF

структурированная система с

поведением теперь может быть определена так:

={(

) |

∈

}. (Г.18)

Чтобы однозначно идентифицировать элементы х множествами

S, пред-

положим, что выборочные переменные из всех множеств

S (

Nx ∈ ) иден-

тифицируются тем же индексом k, что используется для идентификации пе-

ременных во всем множестве S [уравнение (Г.16)]. Соединения С

элемен-

тов

Ny,x ∈ структурированной системы SF

определяются теперь как пере-

сечения множеств выборочных переменных

x,y

∩

(Г.19)

В представлении (Г.18), которое не содержит никаких ограничений на

порядок порождения и на результирующее разбиение переменных из множеств

S (

Nx ∈ ) и S на порождающие и порождаемые переменные, обычно требу-

ется, чтобы для всех пар элементов

Ny,x

∈

выполнялось только одно до-

полнительное условие, а именно следующее уравнение:

SSf[]SSf[

yyxx

∩↓=∩↓ (Г.20)

Это условие обеспечивает то, что проекции функций поведения

для

любой пары элементов из SF

равны относительно их общих переменных (со-

единяющих переменных). По существу, это требование сводится к требованию,

чтобы переменные из разных элементов, считающихся (определяемых) одина-

ковыми, были действительно равны независимо от элементов, в которые они

входят. Будем это требование называть локальной согласованностью по-

ведения.

Как уже говорилось, системы с поведением

,, являющиеся элементами

, на практике часто определяются на локально несогласованных множест-

вах данных и, следовательно, не удовлетворяют требованию локальной согла-

сованности поведения. Для работы с такими структурированными системами в

различных проблемных контекстах, нужно сначала разрешить эти несогласо-

ванности (смотри раздел Г.11). В остальных разделах этой главы считает-

ся, что структурированные системы с поведением локально согласованы.

После определения порядка порождения для структурированной сис-

темы с поведением SF

множество выборочных переменных S и SF

разбива-

ется на порождающие и порождаемые переменные, соответственно обозна-

242

чаемые как

S и

S . Полученная структурированная система должна удовле-

творять требованию однозначности управления. В данном случае это означа-

ет, что любая переменная из S

должна порождаться одним и только одним

элементом структурированной системы. В свою очередь, это значит, что

множества порождаемых переменных

(

∈

), связанные с отдельны-

ми элементами структурированных систем, должны образовывать разбиение

множества S

Взяв один определенный элемент х (

∈

) структурированной систе-

мы SF

, рассмотрим теперь множество переменных

S)SS(

−

∩

Это (с глобальной точки зрения) множество порождаемых переменных,

соединенных с элементом х, но не порождаемых этим элементом. Понятно, что

с локальной точки зрения (отдельный элемент) это входные переменные, хотя

с глобальной точки зрения (структурированная система) они являются порож-

даемыми переменными. Следовательно, сам элемент должен рассматри-

ваться как направленная система, в то время как структурированная система

рассматривается как нейтральная в том смысле, что переменные множества

не разбиты на входные и выходные. Это не значит, что в определении

структурированных систем есть некоторая несогласованность. Это просто

следствие того, что для структурированных систем возможны два сосущест-

вующих подхода - локальный (с точки зрения элементов систем) и глобальный

(рассматривающий структурированную систему как целое). С локальной

точки зрения все элементы, с которыми связан некий элемент, образуют его

среду. Это нечто вроде внутренней среды, определенной только для струк-

турированной системы. С глобальной точки зрения среда (или внешняя

среда) не выделяется. Однако нам представляется, что в данном случае

предпочтительнее рассматривать структурированную систему как направ-

ленную, у которой все переменные из множества V объявлены выходны-

ми.

Теперь остается обсудить только роль множества порождающих пе-

ременных

для отдельных элементов структурированной системы, то есть

значение переменных из множеств

∩

для всех

∈

Состояния этих переменных должны быть доступны данному элементу

на каждом шаге процесса порождения, как того требует функция поведения.

Они могут быть доступны или изнутри, т. е. выводиться обычным образом

из предыдущих состояний, так же как предыдущие состояния порождае-

мых и входных переменных, или снаружи, т. е. через входные переменные,

представляющие соединения с другими элементами структурированной

системы. Таким образом, эти переменные рассматриваются или как порож-

дающие переменные, или как входные переменные элемента. Одну из этих

альтернатив должен выбрать пользователь. В любом случае будем эти пе-

243

ременные обозначать

S. Спецификация их действительной роли входит

в определение системы с поведением, представляющей этот элемент, а

также в определение направленных соединений элементов.

Итак, порождающие системы с поведением, объединяемые в структу-

рированную систему, обычно должны рассматриваться как направленные

системы. Поскольку такой подход возможен всегда, мы определяем

},Nx)F,S,S{(FS

qGB

∈=

)

(Г.21)

понимая, что при этом не требуется никакого содержательного оп-

ределения SF

Под это определение подходит и особый (вырожденный) случай, ко-

гда ни одна из переменных из V не объявляется как входная.

—

это соответственно порождаемые и входные переменные элементов х:

S-

это множество переменных, введенных и рассмотренных в предыдущем

параграфе. В зависимости от того, какая из альтернатив выбрана, в это

множество входят входные или выходные переменные элемента. Как и в

предшествующем определении структурированной исходной системы,

предполагается, что переменные из всех этих трех множеств и все эле-

менты

Nx ∈ идентифицируются индексом b, определенным в уравнении

(Г.16). Для любого

Nx ∈ эти три множества образуют разбиение множе-

ства

S. Кроме того, для некоторого

∈

{0} переменные из множества

входят в соединения

y,x

)

, в то время как переменные из множества

входят только в соединения

x,y

)

, переменные из

S могут входить в со-

единения с любым направлением или вовсе не входить в соединения.

Будем структурированные системы вида (Г.18) или (Г.21) называть

соответственно структурированными системами с поведением основного и

порождающего типа. Понятно, что из структурированной системы с пове-

дением основного типа может быть выведено семейство структуриро-

ванных систем с поведением порождающего типа. Структурированные

системы этого семейства отличаются одна от другой:

1) разбиением S на

S и S

;

2) разбиением

S на )Nx(S

∈

;

3) использованием переменных из множеств )Nx(S

∈

Разбиение 1 определяется разными порядками порождения для пред-

сказания или восстановления. Разбиение 2 определяется перекрытиями пе-

ременных из множества S

с элементами структурированной системы. Го-

воря точнее, переменная из множества S

, входящая в один и только один

элемент, очевидно, должна порождаться этим элементом. С другой сторо-

ны, переменная, входящая в несколько элементов, может порождаться

любым из этих элементов, но только одним из них. Выбор этого элемента

обычно осуществляется исходя из порождающей нечеткости (чем меньше

244

получающиеся порождающие нечеткости, тем предпочтительнее этот вари-

ант), а также некоторыми вспомогательными критериями, определенными

пользователем. Альтернативы типа 3) не влияют на порождающую не-

четкость выбранной структурированной системы. Они представляют собой

просто варианты формального представления. Пользователю должна

быть предоставлена возможность повлиять на выбор представления; если

представление ему безразлично, то нужно использовать один из вариантов

по умолчанию.

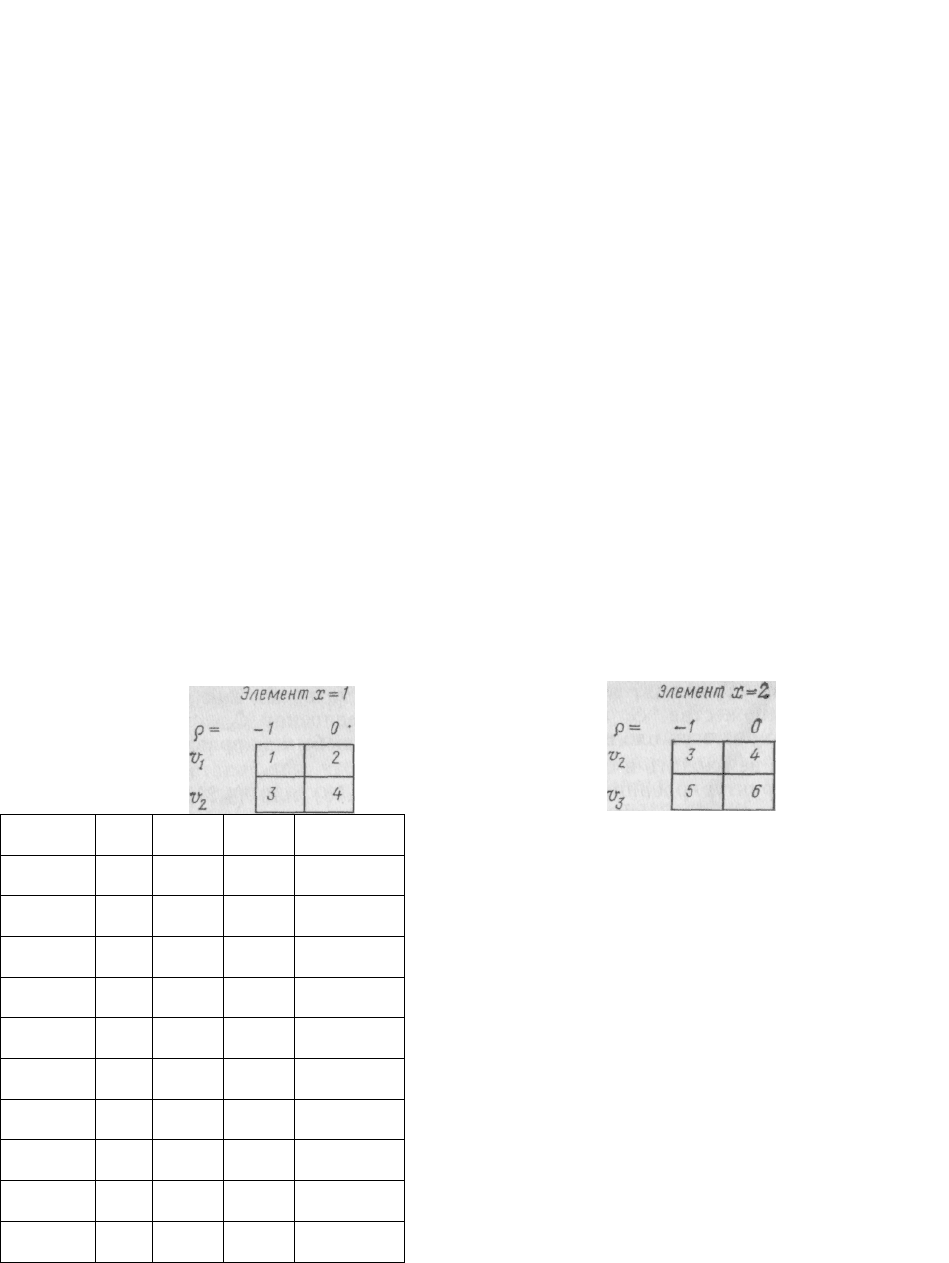
Пример Г.6. Рассмотрим структурированную систему основного типа

(Г.18), состоящую из двух подсистем, базирующихся на одном и том же

полностью упорядоченном параметрическом множестве. Каждый из эле-

ментов состоит из двух бинарных переменных, определяемых вероятност-

ными функциями поведения. Маски

М и

М и функции поведения

показаны соответственно на рисунке Г.5 а и б. Ясно, что эта структуриро-

ванная система удовлетворяет требованию неизбыточности. Она также

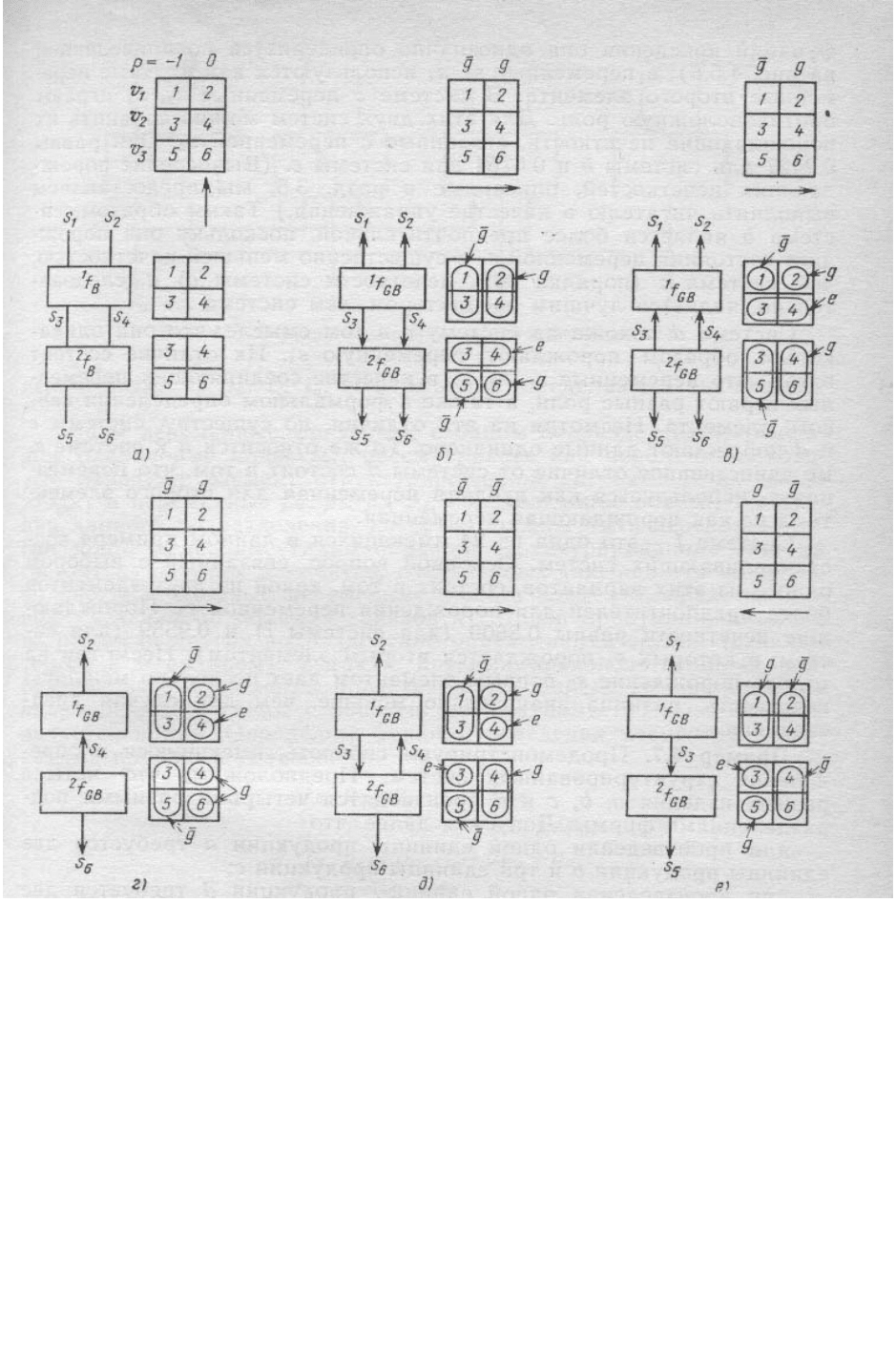
локально согласована, как это показано на рисунке Г.5 б. Полная маска,

схема, а также две частичные маски приведены на рисунке Г.6 а. Осталь-

ные схемы и маски на рисунке Г.6 представляют собой характерные при-

меры некоторых структурированных систем порождающего типа, кото-

рые могут быть получены из этой системы основного типа.

)(f

0 0 0 0.05

0 0 1 0 0.05

0 0 1 1 0.1

0 1 0 0 0.2

0 1 1 0 0.05

0 1 1 1 0.05

1 0 0 1 0.15

1 0 1 0 0.15

1 1 0 1 0.15

1 1 1 0 0.05

245

[

↓{s

, s

}](γ)

[

↓{s

, s

}](γ)

——————————————————

———————————————

γ = 0 0 0.25(= 0.05+0.20)

0.25(= 0.05+0.10+0.10)

0 1 0.30(= 0.15+0.15)

0.30(= 0.05+0.20+0.05)

1 0 0.30(=

0.05+0.05+0.15+0.05) 0.30(=

0.05+0.10+0.10+0.05)

1 1 0.15(= 0.10+0.05) 0.15(= 0.05+0.10)

Рисунок Г.5 - К примеру Г.6

Для вычисления общего числа существенно отличных структу-

рированных систем порождающего типа, которые можно получить из

приведенной в этом примере системы основного типа, предположим, что

соединение со средой содержит все порождаемые переменные, равно как и

все остальные переменные, рассматриваемые как соединяющие пере-

менные. Тогда в этом примере имеются 24 порождающие системы для

каждого из двух порождающих порядков (предсказание, восстановле-

ние). Для целей предсказания они получаются комбинированием сле-

дующих вариантов для переменных: две возможности для переменной

и две для переменно s

(они рассматриваются или как соединяющие,

или нет); возможности для переменной

(она или не рассматривается

как соединяющая, или имеет одно из двух возможных направлений);

два возможных направления для переменной

. Если учитывать оба

порядка порождения, то в данном примере существуют 48

возможных по-

рождающих структурированных систем. Далее варианты любой системы

можно получить, по-разному определяя соединения со средой.

Из 48 вариантов пять, представляющих важнейшие показаны на рисунке

Г.6,б - Г.6,е. Будем для удобства называть их системами

b,c,…,f. Первые

четыре варианта (системы

b — е} предназначены для предсказания, а по-

следний вариант (система

f) для восстановления.

Структурированные системы b и с подобны в том смысле, что и в той

и в другой системе выборочные переменные входят в разные соединения.

Их роль отлична от роли переменных s

, s

. В системе b переменная s

порождается первым элементом

(на языке функций поведения она од-

нозначно определяется по приведенной на рисунке Г.5,б), а переменные s

используются как входные переменные второго элемента. В системе с пе-

ременные s

, s

играют противоположную роль. Для этих двух систем можно

сравнить их порождающие нечеткости, связанные с переменной s

. Они

равны 0,2427 для системы b и 0.6754 для системы c. (Вычисление порож-

дающих нечеткостей, описанные в разделе 3.5, мы предоставляем выпол-

)(f

0 0 0 0.05

0 1 0 0 0.05

0 1 0 1 0.1

0 1 1 0 0.2

1 0 0 0 0.05

1 0 0 1 0.05

1 0 1 0 0.15

1 0 1 1 0.15

1 1 1 0 0.15

1 1 1 1 0.05

246

нить читателю в качестве упражнения.) Таким образом, система b является

более предпочтительной, поскольку она порождает состояния переменной

с существенно меньшей нечеткостью, чем система с (порядка 36% не-

четкости системы с) и, следовательно, является лучшим предиктором,

чем система с.

Система d похожа на систему с в том смысле, что они одинаковым

образом порождают переменную s

. Их отличие состоит в том, что пе-

ременные s

, s

в качестве соединяющих переменных играют разные ро-

ли, а также в формальном определении первого элемента. Несмотря на

эти отличия, по существу, системы с и d порождают данные одинаково.

То же относится и к системе е. Ее единственное отличие от системы d со-

стоит в том, что переменная s

используется как входная переменная для

второго элемента, а не как порождающая переменная.

Система f — это одна из 24 имеющихся в данном примере вос-

станавливающих систем. Основной вопрос, связанный с выбором одного из

этих вариантов, состоит в том, какой из двух элементов более предпочти-

телен для порождения переменной s

. Порождающие нечеткости равны

0.8609 (для системы f) и 0.9559 (для систем, в которых s

порождается

вторым элементом). Несмотря на то, что порождение s

первым элементом

дает несколько меньшую нечеткость, разница значительно меньше, чем для

случая предсказания.

Пример Г.7. Продемонстрируем гибкость, имеющуюся в определении

структурированных систем. Предположим, что четыре разных изделия а,

b, с и d производятся четырьмя разными подразделениями фирмы. Допус-

тим далее, что

для произведения одной единицы продукции а требуется две единицы

продукции b и три единицы продукции с;

для произведения одной единицы продукции d требуется две единицы

247

Рисунок Г.6 - Основной тип структурированной системы с поведе-

нием и некоторые полученные системы порождающего типа

(пример Г.6)

продукции а, одна единица продукции с и четыре единицы продукции b.

Каждое подразделение ежедневно должно знать, сколько продукции

ему необходимо произвести. Соответствующее количество продукции бу-

дем представлять переменными р

, р

, p

. Их значения определяются за-

казом, наличием готового продукта и объемами этого продукта, необходи-

мыми другим подразделениям для производства их собственных продук-

тов. Заказы будем представлять переменными о

, о

, а объемы го-

товой продукции - переменными i

, i

. Эти объемы определяются

значениями p

, p

Будем переменные, связанные с одним подразделением (имеющие

одинаковые индексы), рассматривать как переменные, которые образуют

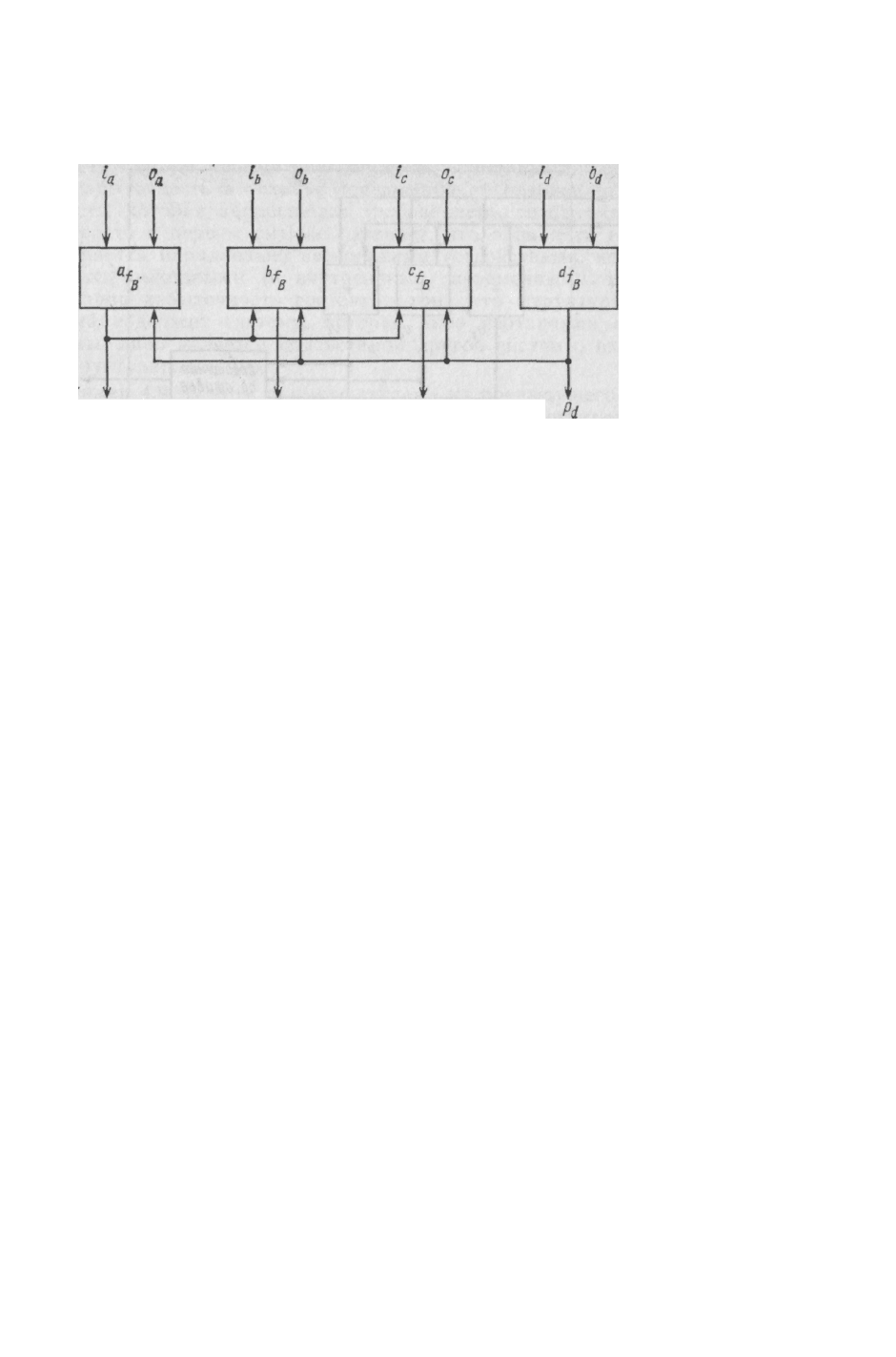
248

элемент структурированной системы. В их число входят и переменные р

, р

, p

, определяющие объемы продукции данного подразделения, кото-

рые должны быть переданы другим подразделениям. Таким образом,

структурированная система состоит из четырех элементов, соединенных

так, как это показано на рисунке Г.7.

Pа

Рисунок Г.7. Структурированная система (пример Г.7)

Входные переменные любого элемента, представляющие сведения об

объемах заказов и готовой продукции, а также потребности других подраз-

делений определяются средой (отделом торговли и складом), а также дру-

гими производственными подразделениями. Элементы представляют собой

детерминированные направленные системы с поведением (без памяти), а

параметром является время. Определим функции поведения элементов сле-

дующими простыми уравнениями:

.iop:f

,ppiop:f

,piop:f

dddB

dacccB

dabbbB

daaaB

−=

++−=

+−=

Пример Г.8. На этом примере будет показано, что требование неизбы-

точности структурированных систем не противоречит тому, что в технике

(в частности, вычислительной технике) для обнаружения и исправления

ошибок часто используются именно избыточные системы. Одна из про-

стейших схем корректирования ошибок состоит в том, что три системы

параллельно выполняют одну и ту же работу, оперируя одними входными

переменными. Подобная схема показана на рисунке Г.8, где три последо-

вательных двоичных сумматора оперируют переменными v

и v

. При

нормальной работе состояния их выходных переменных v

, v

равны,

однако если произошел случайный сбой или если устройство вышло из

строя, то одно значение будет отличаться от двух других, чтобы распознать

подобные ситуации и дать возможность системе в целом продолжить работу,

состояния выходных переменных трех одинаковых устройств оцениваются

двумя специальными системами. Одна из них на рисунке Г.8 называется

«большинство».

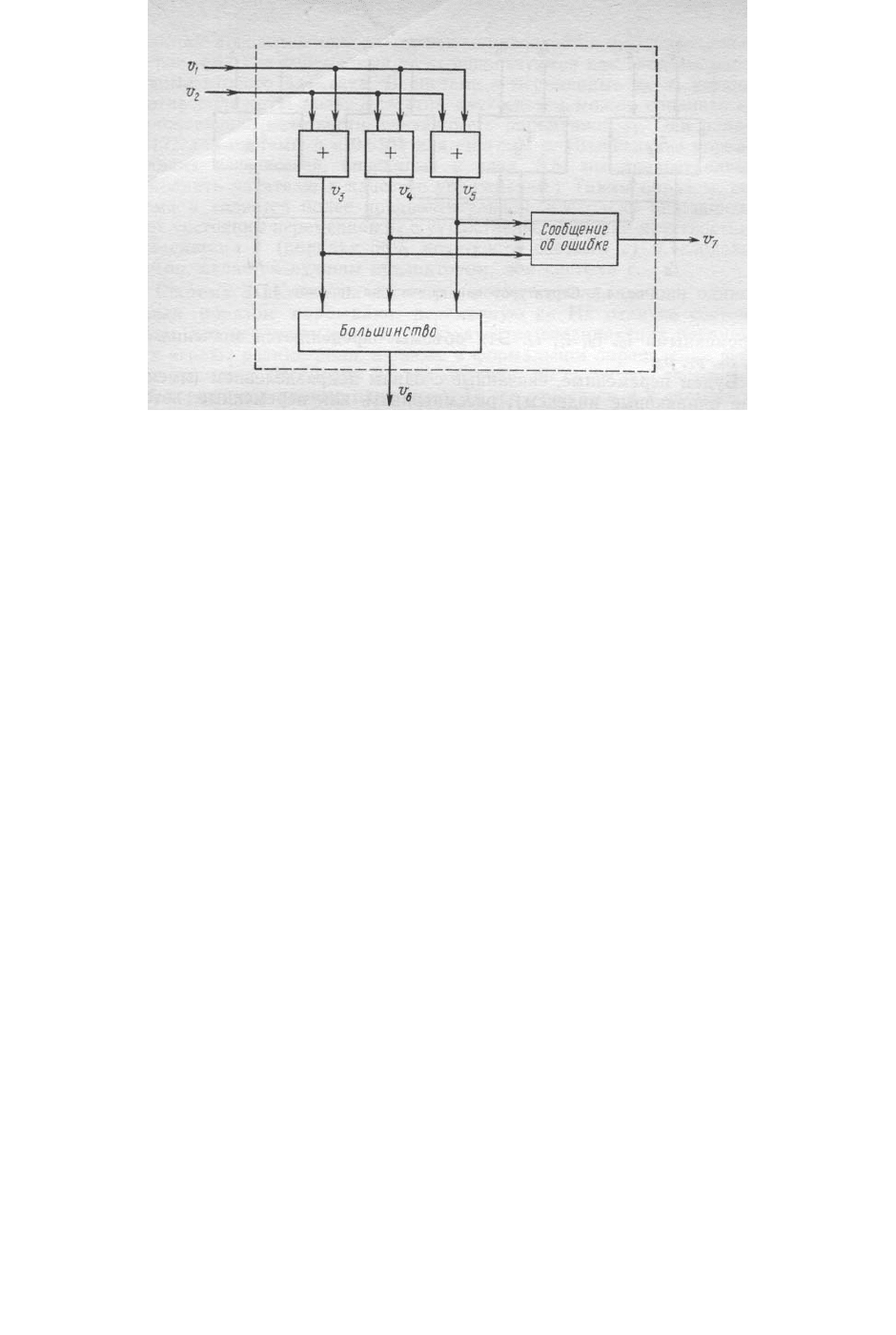
249

Рисунок Г.8 - Простая структурированная система для корректирования

ошибок (пример Г.8)

Она выбирает то состояние выходной переменной (0 или 1), которое

имеют по крайней мере две из трех переменных

, v

, то есть состояние

выходной переменной

равно тому состоянию, которое имеет большинство

входных переменных. Вторая специальная подсистема, названная «сообще-

ние об ошибке» предназначена для обнаружения любой несогласованности

состояний переменных

, v

и для выдачи соответствующего сообще-

ния об ошибке. Ее поведение может быть описано следующим утвержде-

нием:

= l (сообщение об ошибке) тогда и только тогда, когда состояния

переменных

, v

неодинаковы, в противном случае v

= 0 (нормальная

работа). Если сообщения об ошибках появляются редко, это говорит о

случайных сбоях; частое появление таких сообщений говорит о том, что

одно из трех основных устройств (сумматоров) вышло из строя.

Структурированная система, изображенная на рисунке Г.8, удов-

летворяет требованию неизбыточности. Несмотря на то, что система со-

держит две избыточные подсистемы (два из трех сумматоров), они отли-

чаются своими выходными переменными и, если смотреть глубже, свои-

ми внутренними переменными. Таким образом, избыточность в технике

совершенно не похожа на ту избыточность, которая запрещается требова-

нием неизбыточности. Избыточность в первом смысле означает, что одна и

та же работа выполняется параллельно несколькими устройствами, которые

отличаются выходными (и внутренними) переменными. Во втором понима-

нии избыточность состоит в том, что структурированная система содер-

жит систему, которая либо неотличима от другой системы, либо является

подсистемой другой системы, входящей в эту структурированную.

Пример Г.9. В этом примере система из предыдущего примера, изобра-

женная на рисунке Г.8, используется для демонстрации уровней струк-

турного уточнения. Рассмотрим более детально один из блоков на рисунке

250

Г.8 — последовательный двоичный сумматор. Его поведение обычно опи-

сывается следующими уравнениями:

),(modcyxz

tttt

1−

−

(а)

,/)zcyx(c

ttttt

−

(б)

где x

, y

— состояния входных переменных в момент t, равные 0 или 1 (и

упорядоченные по времени в порядке возрастания значений); z

— состоя-

ние выходной переменной (суммарный бит) в момент t; c

t-1

)—состояние

внутренней переменной, представляющей цифру переноса в момент t (t—

1). Согласно этому описанию двоичный сумматор представляет собой

структурированную систему, схема которой изображена на рисунке Г.9,а.

Ее элементы, описанные уравнениями (а), (б), также могут быть детали-

зированы и представлены в виде структурированных систем. Например,

элемент, представляющий уравнение (б), сам может быть представлен как

структурированная система, элементами которой являются стандартные

логические функции от двух переменных (рисунок Г.9,б).

Теперь понятен смысл парных процессов укрупнения и уточнения

структуры. При укрупнении схемы структурированная система корректи-

рования ошибок на рисунке Г.8 является элементом большей структуриро-

ванной системы (арифметического устройства). При дальнейшем структур-

ном укрупнении эта структурированная система становится элементом

еще большей структурированной системы (центрального процессора вы-

числительной машины) и так далее до тех пор, пока не будет достигнут

максимальный уровень, необходимый для конкретного исследования. Но

при уточнении структуры любой элемент системы корректирования оши-

бок (например, сумматор) может рассматриваться как соответствующая

структурированная система (например, та, что изображена на рисунке

Г.9,а), а любой элемент этой структурированной системы также может рас-

сматриваться как структурированная система (рисунок Г.9,б) и так далее

до тех пор, пока не будет достигнут необходимый уровень уточнения.

Два или более уровня структурного уточнения также могут быть объе-

динены в одну систему, то есть в структурированную систему, элементами

которой являются структурированные системы, элементами которых явля-

ются структурированные системы... и так далее. Эта рекурсия, разумеется,

заканчивается на тех элементах, которые не являются структурирован-

ными системами. Будем структурированные системы, содержащие не-

сколько уровней уточнения, называть многоуровневыми структурирован-

ными системами и помечать обобщенным оператором S

, где k — число

уровней уточнения. Например, S

— это двухуровневая структурирован-

ная система с поведением, то есть структурированная система, элементами

которой являются структурированные системы с поведением.