Миронов С.В., Пищухин А.М. Метасистемный подход в управлении

Подождите немного. Документ загружается.

271

например, [f↓{v

, v

}](0 0) =0.312195+0.111628=0.423823 не равно

f(0 0)=0.4,

так что требование для проекций (Г.27) не выполняется. Следовательно, не-

обходимо использовать итеративную процедуру соединения. Последователь-

ность порождаемых процедурой функций поведения сходится к несмещен-

ной реконструкции. Она приводится в таблице Г.10 для i=1, 2, ...,21.

Таблица Г.10 - Последовательность функций поведения, полученных с

помощью базовой и итеративной процедур соединения, пример Г.16

Базовая процедура соединения Итеративная процедура соединения

f*(

f) i = 1 i = 2 i = 3 i = 4 i = 5

0 0 0 0,26 0.312195 0.294647 0.302908 0.309934 0.304982 0.307696

0 0 1 0.15 0.111628 0.105353 0.099904 0.096561 0.095018 0.093371

0 1 0 0.075 0.087805 0.095379 0.088024 0.090066 0.092059 0.089834

0 1 1 0.225 0.188372 0.204621 0.210484 0.203439 0.207941 0.209672

1 0 0 0.13 0.084211 0.094444 0.097092 0.089019 0.091490 0.092304

1 0 1 0.06 0.094118 0.105556 0.100096 0.105580 0.108510 0.106629

1 1 0 0.025 0.015789 0.012977 0.011976 0.010981 0.010418 0.010166

1 1 1 0.075 0.105882 0.087023 0.089516 0.094420 0.089582 0.090328

i = 6 i = 7 i = 8 i = 9 i= 10 i = 11 i= 12 i= 13

0.309608 0.308036 0.308915 0.309511 0.309002 0.309289 0.309481 0.309315

0.092433 0.091964 0.091444 0.091148 0,090998 0.090829 0.090734 0.090685

0.090392 0.091011 0.090314 0.090489 0.090688 0.090462 0.090519 0.090584

0.207567 0.208989 0.209528 0.208852 0.209312 0.209486 0.209266 0.209416

0.090079 0.090826 0.091085 0.090388 0.090626 0.090711 0.090486 0.090563

0.108277 0.109174 0.108556 0.109086 0.109374 0.109171 0.109343 0.109*37

0.009921 0.009761 0.009686 0.009612 0.009561 0.009538 0.009514 0.009498

0.091723 0.090239 0.090472 0.090914 0.090439 0.090514 0.090657 0.090502

i = 14 i = 15 i = 16 i = 17 i = 18 i = 19 i= 20 i = 21

0.309409 0.309472 0.309417 0.309448 0.309469 0.309451 0.309461 0.309468

0.090630 0.090599 0.090583 0.090565 0.090555 0.090549 0.090543 0.090540

0.090510 0.090528 0.090550 0.090525 0.090531 0.090538 0.090530 0.090532

0.209473 0.209401 0.209450 0.209469 0.209445 0.209462 0.209468 0.2C9460

0.090591 0.090518 0.090543 0.090552 0.090528 0.090536 0.090539 0.090531

0.109370 0.109427 0.109457 0.109435 0.109454 0.109464 0.109457 0.109463

0.009490 0.009482 0.009477 0.009476 0.009472 0.009470 0.009470 O.Q0946

0.090527 0.090573 0.090523 0.090531 0,090546 0.090530 0.090532 0.090537

Результаты проверки на сходимость — шаг 4—алгоритм процедуры со-

единения— приведены в таблице Г.11. Отсюда, если ∆>0.15067, то вы-

полнение процедуры завершится при i=3; если ∆>0.004128, то выполнение

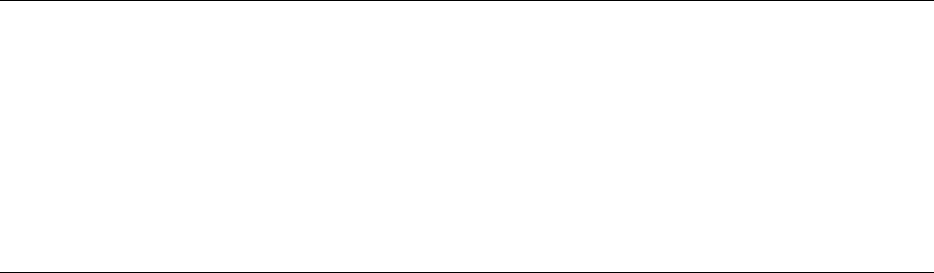
272

завершится при i = 6 и так далее. Так как ∆=0.00002, то процедура завершит-

ся при i = 21.

Таблица Г.11. Проверка на сходимость — шаг 4 итеративной процедуры

соединения из примера Г.16

)q(modi|,f)c(f|

qii

−

—————————————————————————————————

i = 3 i = 6 i = 9 i = 12 i = 15 i = 18 i = 21

0 0 0 0.002261 0.000326 0.000097 0.000030 0.000009 0.000003 0.000001

0 0 1 0.015067 0.004128 0.001285 0.000414 0.000135 0.000044 0.000015

0 1 0 0,002261 0.000326 0.000097 0.000030 0.000009 0.000003 0.000001

0 1 1 0.015067 0.004128 0.001285 0.000414 0.000135 0.000044 0.000015

1 0 0 0.004808 0.001060 0.000309 0.000098 0.000032 0.000010 0.000003

1 0 1 0.011462 0.002697 0.000809 0.000257 0.000084 0.000027 0.000009

1 1 0 0.004808 0.001060 0.000309 0.000098 0.000032 0.00001 0.000003

1 1 1 0.011462 0.002697 0.000809 0.000257 0.000084 0.000027 0.000009

Г.7 Задача реконструкции

Разбиение воспринимаемого мира

на части удобно и, возможно, не-

обходимо, но неизвестно точно,

как, оно должно быть сделано.

Г. Бейтсон

Задача реконструкции может быть сформулирована следующим обра-

зом: дана система с поведением, рассматриваемая как обобщенная система;

требуется определить, какие наборы ее подсистем, а каждый такой набор

рассматривается как гипотетическая реконструкция, подходят для реконст-

рукции заданной системы с заданной точностью, причем реконструкция

должна производиться только по той информации, что содержится в этих

подсистемах.

Укажем, прежде всего, на то, что согласно такой формулировке задачи

понятие «реконструкция» становится более конкретным: при реконструкции

используется вся информация, полученная из подсистем, но только она. Это

означает, что требуется, чтобы реконструкция была несмещенной в том

смысле, как это определилось в разделе Г.6, и, следовательно, можно исполь-

зовать для ее получения соответствующую процедуру соединения.

В задаче идентификации несмещенная реконструкция представляет со-

бой хорошо обоснованную гипотезу (оценку) относительно неизвестной

обобщенной системы причем гипотеза эта строится по заданной структури-

рованной системе. Поскольку истинная обобщенная система неизвестна, то

невозможно определить, насколько близка к ней эта гипотетическая система

В задаче реконструкции несмещенная реконструкция описывает реконструк-

тивные возможности рассматриваемой гипотезы относительно заданной

273

обобщенной системы. Чем ближе несмещенная реконструкция к истинной

(заданной) системе, тем лучше гипотеза.

В общем случае близость двух сопоставимых систем с поведением мо-

жет быть выражена через метрическое расстояние между их функциями по-

ведения. Существует много разных типов метрических расстояний. Так, на-

пример, класс расстояний Минковского определяется следующей формулой:

∑

∈

−=

p/hh

,|)c(f)c(f|[)f,f(

(Г.39)

где

f, f

- соответственно функция поведения заданной системы и несмещен-

ная реконструкция по гипотезе h, a

∈

- параметр функций расстояния.

При

р = 1- это расстояние Хэмминга, при p = 2 - Евклида, при р = ∞ - верхняя

граница расстояний.

Расстояния по Минковскому вычисляют по точечным разностям

|)c(f)c(f|

−

распределение вероятностей или возможностей в соответствии с формулой

(Г.39) . Несмотря на то, что поточечное описание близости

f и f

полезно для

многих приложений, теоретически оно недостаточно хорошо обосновано.

Более обосновано рассматривать близость как разности информации, содер-

жащейся в

h относительно f, или, другими словами, как потерю информации

при замене

f на h (на множество проекций f ).

Меру подобной потери информации будем называть информационным

расстоянием и обозначать

D(f, f

)- Для вероятностных систем она задается

хорошо известной формулой

∑

∈

)c(f

log)c(f

|C|log

)f,f(D

(Г.40)

где константа l/log

|C| — нормирующий коэффициент, обеспечивающий вы-

полнение соотношения

0 ≤

D(f, f

) ≤ 1.

Поскольку, если

(с) = 0, то f(с) = 0, вероятностное информационное

расстояние определено всегда. Это, однако, не метрическое расстояние, так

как оно асимметрично, более того,

D(f

, f) может быть не определено для не-

которых

f и f

[когда f

(с) > 0 и f (c) = 0 для некоторого с

∈

С].

При применении вероятностного расстояния к порождающей системе с

поведением уравнение (Г.40) приобретает следующий вид:

)g|g(f

log)g|g(f)g(f

|G|log

)f,f(D

GgGg

∑∑

∈∈

(Г.41)

Модификация уравнений (Г.40) и (Г.41) для направленных систем с по-

ведением очевидна.

Для возможностных систем информационное расстояние рассчитывает-

ся по формуле

∫

)l,f(c

)l,f(c|

log

|C|log

)f,f(D

, (Г.42)

274

представляющей собой аналог вероятностного информационного расстояния

(Г.40) для

U - нечеткости.

Далее в этом разделе, после соответствующего описания свойств рекон-

структивных гипотез, будет описано применение информационных расстоя-

ний для сравнения этих гипотез.

Реконструктивная гипотеза для заданной обобщенной системы с пове-

дением представляет собой набор ее подсистем. Если обобщенная система

состоит из

n переменных, то число ее подсистем, содержащих по крайней

мере одну переменную равно 2

- 1, а общее число наборов таких подсистем,

содержащих не менее одной подсистемы, равно

−

С ростом n это чис-

ло| растет очень быстро. Однако без потери общности его можно су-

щественно уменьшить, если рассматривать только неизбыточные; наборы

подсистем (смотри раздел Г.3).

Для многих системных исследований очень перспективным является

другой способ сокращения числа реконструктивных гипотез. Он состоит в

исключении наборов подсистем, не содержащих всех переменных обобщен-

ной системы. Это требование, обычно называемое условием покрытия, фор-

мально выглядит так:

∪ ,

где

S — множество переменных из подсистем реконструктивной гипо-

тезы, а

S – множество переменных обобщенной системы. Это условие объяс-

няется прежде всего необходимостью использовать в реконструктивной ги-

потезе информацию обо всех переменных обобщенной системы для того,

чтобы реконструкция была логически возможна. Поскольку вопрос о вклю-

чении или исключении выборочных переменных из обобщенной системы

решается в результате анализа маски (смотри раздел В.6), выполнение усло-

вия покрытия общности не нарушает.

Далее под реконструктивной гипотезой будут пониматься только такие

наборы подсистем заданной обобщенной системы, которые удовлетворяют и

требованию неизбыточности, и условию покрытия. Таким образом, реконст-

руктивная гипотеза — это структурированная система с поведением, сравни-

мая с обобщенной системой с поведением. Однако иногда бывает нужно ра-

ботать со всеми наборами подсистем, которые удовлетворяют только тре-

бованию неизбыточности. Будем такие наборы подсистем называть обоб-

щенными реконструктивными гипотезами. Понятно, что для данной обоб-

щенной системы с поведением множество ее реконструктивных гипотез яв-

ляется подмножеством множества ее обобщенных реконструктивных гипо-

тез.

Любая реконструктивная гипотеза (равно как и любая обобщенная ре-

конструктивная гипотеза) полностью описывается:

1) семейством подмножеств входящих в нее переменных,

2) функциями поведения, соответствующими отдельным под-

множествам переменных.

275

Если опустить свойство 2, то свойство 1 определяет класс ин-

вариантности реконструктивных гипотез, отличающихся друг от друга

только функциями поведения их элементов. Этот класс инвариантности для

того, чтобы отличать его от отдельных реконструктивных гипотез класса,

будем называть структурой. Напомним, что каждая отдельная ре-

конструктивная гипотеза представляет собой конкретную

структурированную систему. Таким образом, структура - это свойство

структурированной системы, инвариантное относительно изменения

функций поведения ее элементов. Для данного множества переменных, скажем множества

S, множество

структур, представляющих все реконструктивные гипотезы любой обобщен-

ной системы, определенной на

S, состоит из семейств подмножеств S, удов-

летворяющих условиям неизбыточности и покрытия. Будем для удобства

представлять все множества переменных одной мощности, скажем мощности

n, общим множеством структур, скажем множеством G

, определенным на

множестве

положительных целых чисел. Формально для любого

n ∈

= {G

G),N(P⊂ удовлетворяет условиям неизбыточности и по-

крытия}.

В этом формальном определении через

обозначены элементы G

, яв-

ляющиеся наиболее общими структурами, рассматриваемыми при решении

задачи реконструкции (некие специальные типы этих структур будут введе-

ны ниже); индекс

i идентифицирует структуры из G

и обычно

|G|

Ni ∈ . Мно-

жество

тривиально интерпретируется на языке любого множества пере-

менных

S, такого, что |S| = n, заданием взаимно однозначного отображения

переменных из

S на целые из N

. Будем для удобства структуры из мно-

жеств

называть G-структурами.

Из некоторых соображений удобно расширить множество G

до

множества G

всех обобщенных реконструктивных гипотез. Формально

для любого n∈N

={G

G),N(P⊂ удовлетворяет условию неизбыточности}.

Несмотря на то, что далее в этой главе основное внимание будет уде-

ляться множествам G

, все результаты относительно G

могут быть легко

обобщены и на множества G

Если множество G

для некоторого определенного п получает кон-

кретную интерпретацию в контексте некой обобщенной системы с поведе-

нием с п переменными, то структуры в G

представляют собой однознач-

ные представления реконструктивных гипотез, связанных с этой обобщен-

ной системой. Это непосредственно следует из того факта, что функции по-

ведения, соответствующие любым подмножествам переменных, определя-

ются однозначно как соответствующие проекции обобщенной функции по-

ведения. Следовательно, реконструктивные гипотезы могут изучаться в ви-

де абстрактных структур. Данная структура из G

становится конкретной

реконструктивной гипотезой, когда интерпретируется в контексте сравни-

мой с ней определенной обобщенной системы с поведением (то есть систе-

мы с п переменными).

276

Основным вопросом задачи реконструкции является разработка эффек-

тивных вычислительных процедур, допускающих представление, оценку и

сравнение реконструктивных гипотез, представленных всеми структурами

для данного множества переменных. Это очень непростая задача, посколь-

ку, как будет показано ниже в этом разделе, число структур растет очень

быстро. Для успешного решения этой задачи необходимо использовать соот-

ветствующее упорядочение и классификацию структур.

Определим сначала естественное упорядочение структур, называемое

уточняющим упорядочением. Пусть даны две структуры G

, G

&∈ Будем

называть G

уточнением G

(и, соответственно, G

укрупнением G

) тогда

и только тогда, когда для любого x

∈

существует

Gy ∈ , такое, что

⊆ ; пусть G

≤ G

означает, что G

это уточнение G

Рассмотрим две структуры G

, G

∈

, такие, что G

≤ G

. Тогда G

назы-

вается непосредственным уточнением G

(a G

— непосредственным укрупне-

нием G

) тогда и только тогда, когда не существует G

&∈ , такого что

&∈

и G

≤ G

. Для заданной структуры G

∈

структурное соседство оп-

ределяется как множество всех непосредственных уточнений и непосред-

ственных укрупнений G

в &

Легко видеть, что отношение уточнения определяет частичное упорядо-

чение. Более того, пара ( &

≤ ) определяет решетку, что подтверждают сле-

дующие факты: 1) существует универсальная верхняя граница — множество

}; 2) существует универсальная нижняя граница - множество

{{x}|

Nx ∈ }; 3) для любой пары G

, G

∈

наибольшим общим уточне-

нием является неизбыточный эквивалент множества

{

Gy,Gx|yx ∈∈∩ }; 4) для любой пары G

, G

∈

наименьшим общим

укрупнением является неизбыточный эквивалент множества

GG ∩ . Будем

называть эти решетки решетками уточнения G-структур). (по одной для

каждого

n ∈ ). Отметим, что уточняющее упорядочение применимо и к

множествам G

, что дает решетки (&

,≤ ).

Понятно, что решетка уточнения или некая нужная ее часть может

быть получена с помощью неоднократного выполнения процедуры, порож-

дающей все непосредственные уточнения для любой структуры из решетки.

Одна такая процедура определяется следующим образом.

Уточняющая процедура для G-структур (или RG-процедура). Заданы G-

структуры G

S|k∈N

}∈&

. Для определения всех их непосредственных

уточнений

1) положить k = 0;

2) если k<q, то k+1→k, иначе перейти на шаг 5;

если |

| ≥ 2, то

S})

∪

X→R,

где

X={x

⊂

x| =|

S| - 1}; иначе перейти на шаг 2;

4) R→Q, где Q — неизбыточный аналог R, записать Q в качестве непо-

средственного уточнения G

, перейти на 2;

5) конец.

277

Обратите внимание на то, что условие |

S| ≥ 2 из шага 3 обеспечивает

то, что порождаемые структуры будут удовлетворять условию покрытия;

замена этого условия на условие |

S| ≥ l позволяет работать с множества-

ми &

обобщенных реконструктивных гипотез. Шаг 4 обеспечивает выпол-

нение условия неизбыточности. Тот факт, что наименьшее возможное из-

менение делается на шаге 3, т. е. только один элемент G

изменяется на не-

посредственно следующие меньшие элементы (подмножества), обспечивает

то, что порождаемые структуры являются непосредственными уточнениями

Пример Г.17. Дано G

= {

S= {1, 2, 3},

S={2, 3, 4},

S={1, 4}}.

Сразу видно, что для всех 2

≥

∈

|S|Nk

, и, следовательно, RG-процедуры

применимы к любому элементу. Таким образом, имеются три непосредст-

венных уточнения G

. Множество

S заменяется на множества {1, 2}, {1,

3}, {2, 3}, однако третье множество является подмножеством и будет ис-

ключено на шаге 4; это даст следующее непосредственное уточнение:

{{1, 2}, {1, 3}, {2, 3, 4}, {1, 4}}.

Аналогичная замена

S дает второе непосредственное уточнение:

{{1, 2, 3}, {2, 4}, {3, 4}, {1, 4}}.

Наконец, множество

S заменяется на множества {1} и {4}, которые

являются избыточными и будут исключены на шаге 4; отсюда имеем третье

непосредственное уточнение:

{{1, 2, 3}, {2, 3, 4}}.

Для сокращения вычислительной сложности порождения ре-

конструктивных гипотез полезно разбить решетки уточнения на подходящие

классы эквивалентности по уровню вычислений. Тогда эти классы эквива-

лентности могут быть представлены соответствующими каноническими

структурами, а уточняющие процедуры разработаны для этих канонических

представлений разных уровней вычислительной сложности. Чтобы проде-

монстрировать этот подход, предположим, что описаны только два уровня вы-

числений, называемые локальным и глобальным.

Локальный уровень вычислений представлен уже описанной RG-

процедурой. Для определения глобального уровня вычислений определим

функции

,Nn,RG:r

nnn

∈

→

где R - множество симметричных и рефлексивных бинарных отношений, оп-

ределенных на множестве N

(они также называются отношениями сравне-

ния, отношениями толерантности или неориентированными графами с цик-

лами), a r

) — бинарное отношение, выполняемое для целых а и b (a,

b∈N

) тогда и только тогда, когда и а, и b принадлежат по крайней мере

одному из подмножеств N

, входящих в G

. Формально

})xbиxa)(Gx(|)b,a{()G(r

iin

∈

∃

= .

278

Будем элементы R

называть графами. Однако мы должны помнить, что

эти графы не ориентированы (симметричность) и содержат циклы (рефлек-

сивность). Некоторые примеры функций классов r

и r

показаны на рисунке

Г.15. При изображении этих графов опущены тривиальные циклы в узлах.

Рисунок Г.15. Примеры функции r

Понятно, что функции r

сюръективны, а при n ≥ 3 прообразы могут

состоять из более чем одного элемента. Поэтому они индуцируют следующее

отношение эквивалентности на соответствующих множествах G

G-

структур: G

≡

тогда и только тогда, когда G

, G

∈

и r

) = r

)

для некоторого

∈

. Если G

= G

, то мы говорим, что структуры G

и G

r-эквивалентны. Для обозначения классов эквивалентности, индуцируемых

на &

, будем использовать стандартную запись &

Для любого

Nn ∈ множество R

и отношение подмножества (или, ина-

че, операции объединения и пересечения множеств) определяют булеву ре-

шетку. Очевидное взаимнооднозначное соответствие между &

и R

инду-

цирует изоморфную булеву решетку на множестве G

. Этот изоморфизм

позволяет нам порождать классы эквивалентности на &

с помощью соот-

ветствующих операций на графах из R

. При этом, однако, желательно, что-

бы любой класс эквивалентности из &

был представлен некоей канони-

ческой структурой. С этой целью введем для любого

∈

следующие под-

множества &

, в которое входят те G-структуры G

из множества &

, которые состоят

из максимально сочетаемых классов, соответствующих графу

) или, но

в другой терминологии, основанных на кликах этого графа. Подобные

структуры называются также полными покрытиями

). Будем обозна-

чать структуры

из G

и называть С-структурами. Примерами С-структур

являются структуры

и G

, изображенные на рисунке Г.15.

, в которое входят те G-структуры из &

, элементы которых состоят из

пар, связанных на графе

) узлов (обозначаемых целыми числами), или

являются отдельными изолированными узлами. Будем структуры из множе-

ства &

называть Р-структурами и обозначать через P

. Примером Р-струк-

туры является структура

на рисунке Г.15.

Из этих определений и из того факта, что множество всех максимально

сочетаемых классов для любого неориентированного графа единственно,

следует, что любой класс эквивалентности из &

содержит в точности одну

)=r

)

279

С-структуру из &

и одну Р-структуру из P

. Таким образом, С- и Р-

структуры могут рассматриваться как два канонических представления клас-

сов r-эквивалентности G-структур. Каждый класс r-эквивалентности, пред-

ставленный графом, описывается двумя каноническими структурами - наиме-

нее уточненной С-структурой и наиболее уточненной Р-структурой. Взаимно

однозначное соответствие между R

и G

(или P

) индуцирует булеву ре-

шетку на G

(или на P

), изоморфную естественной булевой решетке, опреде-

ленной на P

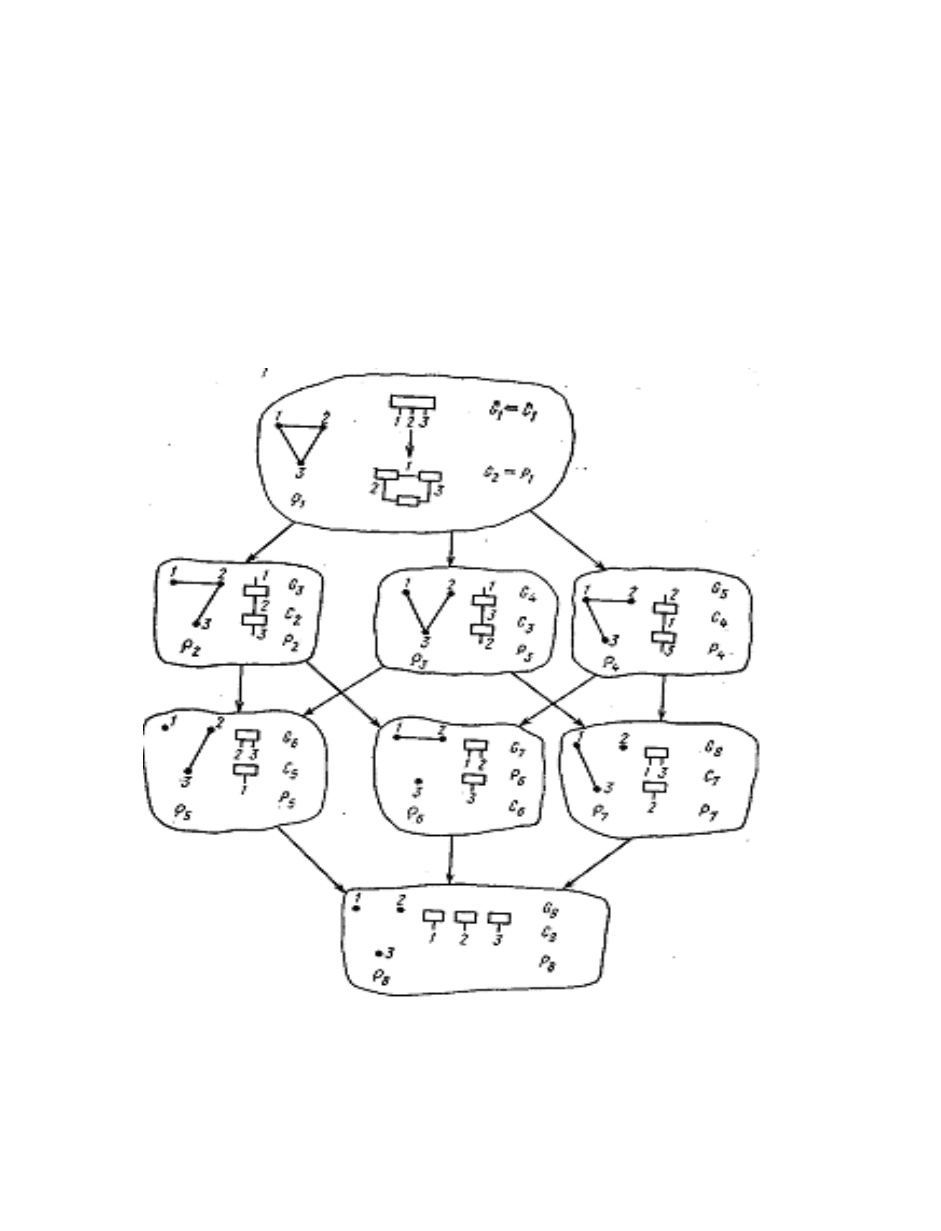
Например, на рисунке Г.16 показаны решетка (&

,≤) и взаимно

изоморфные булевы решетки, определенные на R

, G

, P

и &

Рисунок Г.16 – Решетка (&

,≤) и булевы решетки, определенные на R

, P

, &

Для описания больших решеток полезно определить отношение эквива-

лентности

≡

на множествах &

следующим образом:

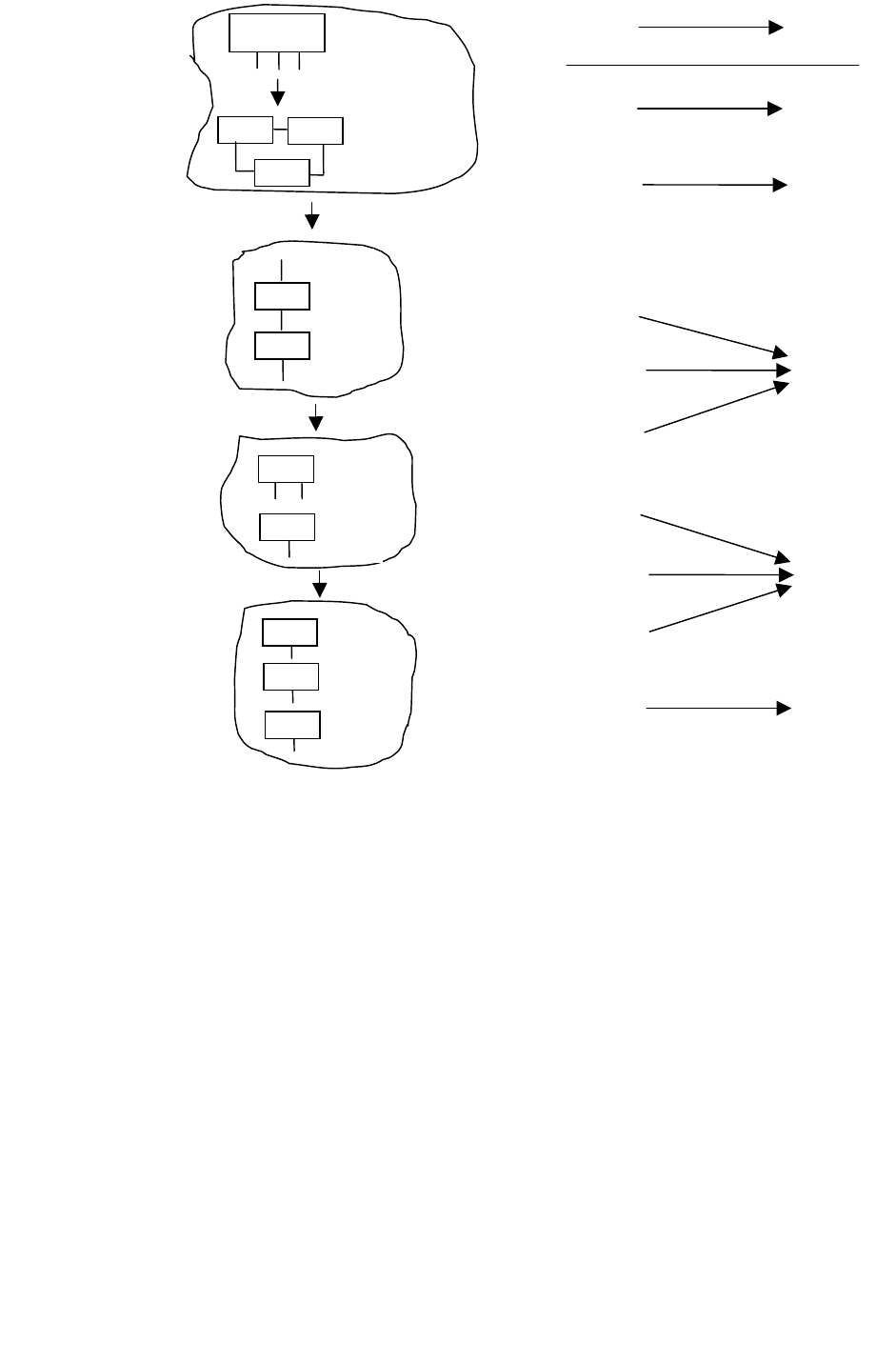
280

Рисунок Г.17 – Решетка (&

, ≤ ) и гомоморфное отображение &

→&

≡

тогда и только тогда, когда G

, G

∈

и G

, G

изоморфны (то

есть когда одна структура может быть получена из другой только переста-

новкой целых чисел из N

, напоминаем, что каждое целое число соответствует

узлу). Будем

≡

называть i - эквивалентностью и обозначать через &

/i мно-

жество классов эквивалентности изоморфных структур (или перестановоч-

ных классов эквивалентности), определенных на &

Пример, демонстрирующий смысл i-эквивалентности, приведен на ри-

сунке Г.17, где обозначенные полужирным шрифтом G

(k∈N

) показы-

вают классы эквивалентности в &

/i. На рисунке Г.17,а показана

решетка (&

/i, ≤). Это та же самая решетка, что и на рисунке Г.16, но уп-

рощенная, так как на ней не различаются изоморфные структуры. Сделано

это за счет удаления меток входов в блоки на схеме и включения только од-

ной схемы для каждого перестановочно эквивалентного класса. Структуры

в каждом классе легко определяются перестановкой целых 1, 2, 3 для входов в

блоки. Упрощенная решетка на рисунке Г.17,в является гомоморфным образом

решетки, изображенной на рисунке Г.16. Гомоморфное отображение, являю-

щееся основой данного упрощения, показано на рисунке Г.17д

а)

)