Миронов С.В., Пищухин А.М. Метасистемный подход в управлении
Подождите немного. Документ загружается.


261
в) p
5
≥ 0 дает p
0
≥0.2;
г) р
6
≥ 0 дает p
0
≥0.3.
Так как должны выполняться все эти ограничения, из неравенств сле-
дует, что р
0
должно принимать значения в диапазоне
0.3 ≤ p
0
≤ 0.4
Если задаться значением р
0
из этого диапазона, то из уравнений а) —
г) можно однозначно определить значения неизвестных. В таблице Г.5
показано, как таким образом определяется реконструктивное семейство для
данного примера.
v
1
v
2
1
f(
1
c) v
2
v
3
2
f(
2
c)
———————— ————————
0 1 0.3 0 0 0.1
1
c = 1 0 0.5
2
c = 0 1 0.4
1 1 0.2 1 1 0.5
Таблица Г.5 - Реконструктивное семейство из примера Г.11
v
1
V
2
v
3
p
i
=
f
(с)
с = 0 0 0 0.3 ≤ p
0
≤ 0.4
0 1 1 p
1
= 0.4 -р
0
0 0 0 p
2
= 0.4 - р
0
0 1 1 p
3
= -0.1+р
0
1 0 0 p
4
= 0.4 - р
0
1 1 1 p
5
= - 0.2 + р
0
1 0 0 p
6
= -0.3 + р
0
1 1 1 p
7
= 0.4 - р
0
При определении реконструктивного семейства этой системы будем ис-
пользовать для неизвестных те же обозначения, что и в примере Г.11. То-
гда реконструктивное семейство будет описываться неравенствами
(
)
70,i
Nip ∈≤ и следующими восемью уравнениями:
p
0
+ p
1
= 0.0, (1) p
0
+ p
4
= 0.1, (5)
p
2
+ p
3
= 0.3, (2) p
1
+ p
5
= 0.4, (6)
p
4
+ p
5
= 0.5, (3) p
2
+ p
6
= 0.0, (7)
p
6
+ p
7
= 0.2, (Г) p
3
+ p
7
= 0.5, (8)
Из уравнений (1), (7) и неравенств имеем р
0
= р
1
= р
2
= р
6
= 0. Отсюда
просто определить оставшиеся вероятности:
р
3
= 0.3, р
4
= 0.1, р
5
= 0.4, р
7
=
0.2. Следовательно, в данном случае идентификация однозначна. То есть
данный пример — это пример одного из тех редких случаев, когда «целое
равно сумме составляющих его частей».
Пример Г.13. Чтобы продемонстрировать более общий тип ре-
конструктивного семейства, рассмотрим структурированную систему из трех
(степень свободы)

262
элементов, причем каждый элемент содержит три переменных v
1
,v
2
,v
3
. Пусть
v
1
и v
2
принимают состояния из множества {0, 1}, а v
3
– из множества {0 1,
2}. Элементы представляют собой вероятностные системы с поведением без
памяти. Их функции поведения
l
f,
2
f,
3
f приведены в таблице Г.6.
Таблица Г.6 - Элементы структурированной системы из примера Г.13.
v
1
v
2
1
f(
1
c) v
2
v
3
2
f(
2
с)
v
1
v
3
3
f(
3
с)
1
c = 0 0 0.25
2
с =0 0 0.17
3
с= 0 0 0.11
0 1 0.18 0 1 0.16 0 1 0.14
1 0 0.20 0 2 0.12 0 2 0.18
1 1 0.37 1 0 0.14 1 0 0.20
1 1 0.18 1 1 0.20
1 2 0.23 1 2 0.17
Будем использовать приведенные в таблице Г.7 обозначения неизвест-
ных вероятностей состояний полной системы.
Таблица Г.7- Обозначения, используемые в примере Г.13
v
1
v
2
v
3
f
(с)
с = 0 0 0 f(000) = p
0
0 0 1
f(001) = p
1
0 0 2
f(002) = p
2
0 1 0 f(010) = p
3
0 1 1 f(011) = p
4
0 1 2 f(012) = p
5
1 0 0 f(100) = p
6
1 0 1 f(101) = p
7
1 0 2 f(102) = p
8
1 1 0 f(110) = p
9
1 1 1 f(111) = p
10
1 1 2 f(112) = p
11
Составление уравнений, описывающих реконструктивное семейство, и
определение их решений при ограничениях
p
i
≥ 0 (
10,
Ni
∈
) предоставим
читателю. Скажем только, что система из 16 исходных уравнений с 12 не-
известными сводится к 10 линейно-независимым уравнениям с двумя степе-
нями свободы. Если предположить, что свободными являются неизвестные
р
10
и р
11
, то мы получим следующие неравенства:
263
..pp.
,.p.
,.p.
340230
170050
180040
1110
11
10
≤+≤
≤≤
≤
≤
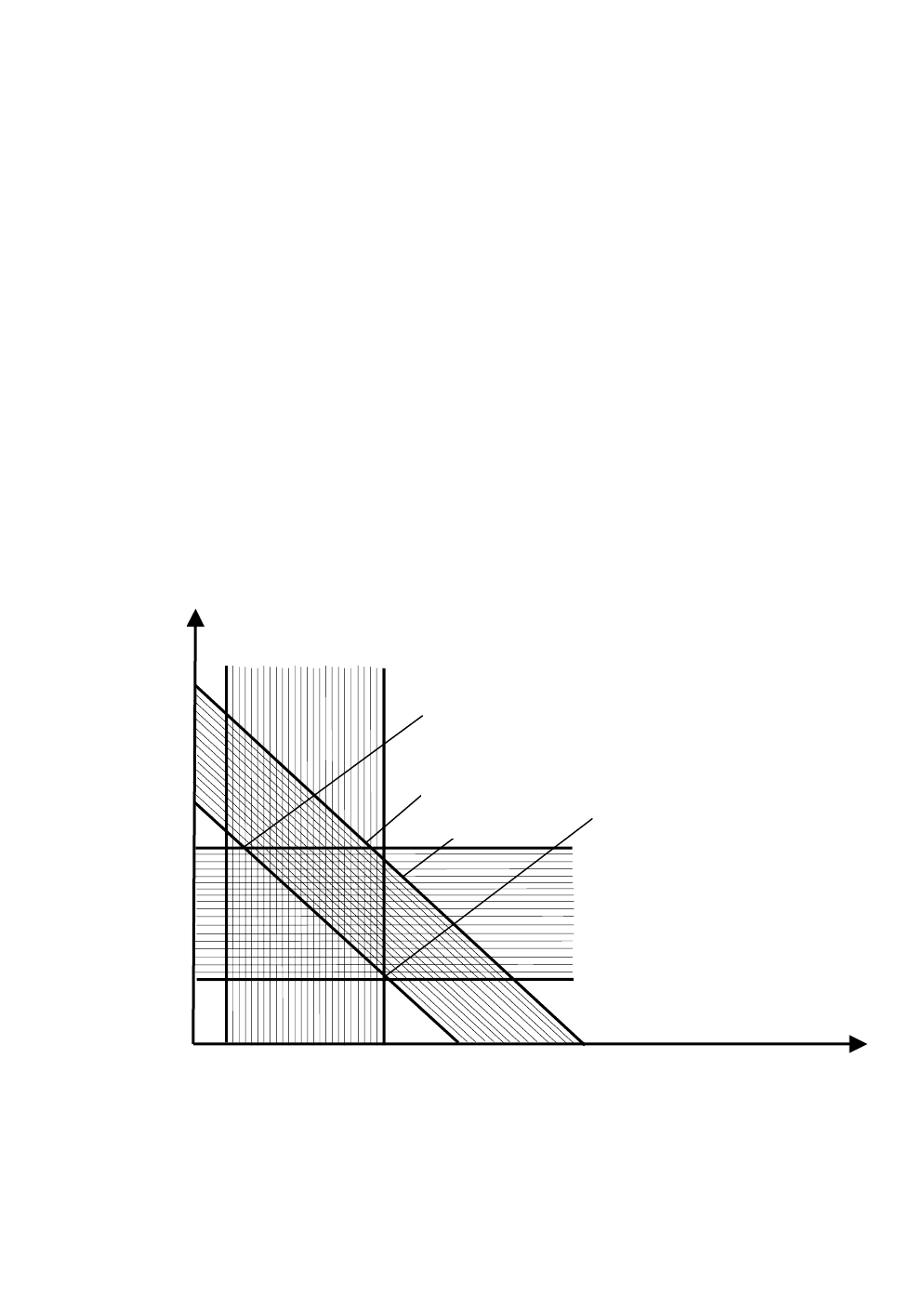
Область значений для р
10
и р
11
, определяемая этими уравнениями, пока-
зана на рисунке Г.14; это выпуклое множество, натянутое на четыре точки
(0.06, 0.17), (0.17, 0.17), (0.18, 0.16), (0.18, 0.05). Для любой пары значений
р
10
и р
11
из этой области значения остальных неизвестных однозначно опре-
деляются следующим образом:
р
0
= 0.34 - р
10
- р
11
,
p
1
= - 0.04 + р
10
,
р
2
= - 0.05 + р
11
,
р
3
= - 0.023 + р
10
+ р
11
,
р
4
= 0.18 – р
10
,
р
5
= 0.23 – р
11
,
р
6
= - 0.17 + р
10
+ р
11
,
р
7
= 0.20 – р
10
,
р
8
= 0.17 – р
11
,
р
9
= 0.37 – р
10
- p
11
.
Пример Г.14. Рассмотрим структурированную систему, элементами ко-
торой являются возможностные системы с поведением с теми же наборами
переменных, что и в примере Г.12. Функции поведения элементов приве-
дены в таблице Г.8. Как видно, они не нормализованы.
0.05 0.1 0.15 0.25 0.3
0.35
0.2
p
10
0.05
0.1
0.15
0.2
0.25
0.3
p
11
Рисунок Г.14 – Описание реконструктивного семейства из примера Г.13
(0.06 – 0.17)
(0.17 – 0.17)
(0.18 – 0.16)
(0.18 – 0.05)

264
Для описания реконструктивного семейства этой структурированной сис-
темы снова воспользуемся обозначениями из таблицы Г.4. Тогда реконструк-
Таблица Г.8 - Элементы структурированной системы из примера Г.14
v
1
v
2
1
f(
1
с)
v
2
v
3
2
f(
2
c)
1
с = 0 0 0.8
2
c = 0 0 0.8
0 I 0.5 0 1 0.9
1 0 0,9 I 0 0.8
1 1 0.8 1 1 0.6
тивное семейство определяется неравенствами p
i
≥ 0 (
70,
Ni
∈
) и следующи-
ми восемью уравнениями в виде (Г.29):
max(p
2
, p
3
)= 0.5, (1) max( p
0
, p
4
)= 0.8, (5)
max(p
3
, p
7
)= 0.6, (2) max( p
2
, p
6
)= 0.8, (6)
max(p
0
, p
1
)= 0.8, (3) max( p
4
, p
5
)= 0.9, (7)
max(p
6
, p
7
)= 0.8, (Г) max( p
1
, p
5
)= 0.9, (8).
Из уравнения (1) следует, что ни р
2
, ни р
3
не могут быть больше 0.5;
следовательно, из (6) следует, что р
6
= 0.8, а из уравнения (2), что р
7
= 0.6.
Из уравнения (5) следует, что р
4
не может быть больше 0.8, а значит, из
уравнения (7) следует, что p
5
= 0.9. Согласно этим результатам данная сис-
тема может быть сведена к двум независимым подсистемам уравнений
max(p
2
, p
3
)= 0.5,
max(p
0
, p
1
)= 0.8,
max( p
0
, p
4
)= 0.8
Единственное уравнение при условии, что р
2
≥ 0 и р
3
≥ 0, имеет решение
р
2
=0.5 и 0 ≤ p
3
≤0.5
или
р
3
=0.5 и 0 ≤ p
2
≤0.5.
Пара уравнений, при условии, что р
0
≥ 0, р
1
≥ 0 и р
4
≥ 0, имеет решение
р
0
=0.8 и 0 ≤ p
1
≤0.8, а также 0 ≤ p
4
≤0.8
или
р
1
= p4=0.8, и 0 ≤ p
0
≤0.8.
B данном реконструктивном семействе легко выделить одно максималь-
ное и четыре минимальных распределения возможностей. Они приведены в
таблице Г.9, где через f
SP
и f
SFi
(
4
Ni
∈
) обозначены соответственно макси-
мальное и минимальные распределения, а через SF — рассматриваемая cтр-
уктурированная система. Реконструктивное семейство состоит из этих четы-
рех распределений, а также из всех распределений, находящихся между мак-
симальным распределением и любым из четырех минимальных.
Для возможностных структурированных систем известно, что в общем
случае их реконструктивные семейства всегда имеют вид, что и в примере

265
Г.14. То есть реконструктивное семейство всегда содержит одно максималь-
ное семейство (предполагается, что данная структурированная система согла-
Таблица Г.9 - Максимальное и минимальные распределения возможностей
для реконструктивного семейства из примера Г.14
v
1
v
2
v
3
f
SF
f
SF,1
f
SF,2
f
SF,3
f
SF,4
C = 0 0 0 0.8 0.8 0.8 0 0
0 0 1 0.8 0 0 0.8 0.8
0 1 0 0.5 0.5 0 0.5 0
0 1 1 0.5 0 0.5 0 0.5
1 0 0 0.8 0 0 0.8 0.8
1 0 1 0.9 0.9 0.9 0.9 0.9
1 1 0 0.8 0.8 0.8 0.8 0.8
1 1 1 0.6 0.6 0.6 0.6 0.6
сована) и множество решений, состоящее из возможностных распределений,
находящихся между максимальным решением и одним из нескольких мини-
мальных решений. Более того, возможность любого полного состояния пере-
менных, входящих в любое минимальное решение, равна или возможности
этого состояния в максимальном решении, или нулю. Данный результат, рав-
но как и некоторые другие результаты, связанные с задачей определения ре-
конструктивного семейства для заданной структурированной системы, полу-
чены недавно и для возможностных, и для вероятностных систем.
КОЭФФИЦИЕНТ ИДЕНТИФИЦИРУЕМОСТИ
Часто необходимо иметь подходящую меру для оценки размера рекон-
структивного семейства. Если эта мера является адекватной, то ее можно ис-
пользовать для оценки нечеткости, связанной с реконструкцией обобщенной
системы по заданной структурированной системе, а также как степень иден-
тифицируемости реальной структурированной системы.
Для возможностных систем размер реконструктивного семейства адек-
ватно оценивается произведением
)]c(f[П
SF
Ас
+
∈
1 (Г.30)
где
f
SF
- максимальный элемент реконструктивного семейства F
SF
, а A -
множество всех полных состояний, для которых степень возможности в ре-
конструктивном семействе определяется не единственным образом [то есть
множество полных состояний, для которых решение ограниченной системы
уравнений вида (Г.29) не единственное]. Обратите внимание, что это произ-
ведение всегда больше или равно 1 и что его значение пропорционально
мощности множества А и значениям
f
SF
(с); оно равно 1 только тогда, когда
множество А пустое (то есть если существует единственное решение.
Если принять произведение (Г.30) в качестве разумной оценки размера
реконструктивного семейства, то естественно было бы определить реконст-

266
руктивную нечеткость u
SF
, связанную со структурированной системой SF,
как логарифм этого произведения, то есть
∏
∑
∈
∈
+=+=
Aс
Ac
SFSF
SF
)]c(f[log)]c(f[logu11
22
. (Г.31)
Понятно, что
|,C|u
SF
≤
≤
0
где считается, что |С| - реконструктивная нечеткость всего множества
G
SF
обобщенных систем, сопоставимых с SF. Можно использовать меру
,
|C|
u
|C|
u|C|
I
SFSF
SF
−=
−
= 1
(Г.32)
называемую коэффициентом идентифицируемости, в качестве разумного по-
казателя возможности определения единственной обобщенной системы по
заданной структурированной системе SF. Понятно, что
.I
SF
10
≤
≤
I = 1 только тогда, когда |
F
SF
| = 1; I
SF
= 0 только тогда, когда
|А| = |С| , и
f
SF
(с) = 1 для всех
С
с
∈
.
Коэффициент идентифицируемости бывает полезен при решении неко-
торых системных задач, особенно при сравнительных исследованиях струк-
турированных систем. В общем случае значительно легче определить коэф-
фициент идентифицируемости структурированной системы, чем реконструк-
тивное семейство: для этого достаточно определить максимальное решение и
состояния с единственными решениями (то есть С - А).
Пример Г.15. Определим коэффициент идентифицируемости структури-
рованной системы, определенной в примере Г.14. Отметим, что в этом при-
мере |С|=8, а множество А состоит из первых пяти состояний, перечисленных
в таблице Г.9. Используя значения
f
SF
(с) для этих состояний, получим рекон-
структивную нечеткость
...log.logu
SF
7143512813
22
=
+
=
Отсюда
I
SF
= 1 — 3,714/8 = 0.536.
ЕДИНСТВЕННЫЙ ВЫБОР ИЗ РЕКОНСТРУКТИВНОГО СЕМЕЙ-
СТВА
Рассмотрим теперь вторую подзадачу задачи идентификации—задачу
выбора из реконструктивного семейства одной обобщенной системы как ги-
потезы о реальной обобщенной системе. Эта задача тривиальна, если рекон-
струкция однозначна (то есть если I
SF
= 1).
В остальных случаях (если данная структурированная система SF со-
гласована и, следовательно
f
SF
≠ 0, этот выбор совершенно произволен, если
только мы не определим некий критерий и не потребуем, чтобы система, вы-
бранная из реконструктивного семейства, наилучшим образом удовлетворяла
этому критерию. В этом случае задача выбора превращается в задачу опти-
мизации с последующим произвольным выбором из лучших, с точки зрения
267
данного критерия, систем. Если исполнительный критерий оптимизации
обеспечивает единственность оптимизации, то из данной задачи исключается
элемент произвольности.
Критерии оптимизации всегда используются исходя из неких фундамен-
тальных соображений и, следовательно, определяются этими соображения-
ми. С эпистемологической точки зрения самым существенным соображением
для выбора обобщенной системы является ее максимальная независимость со
всех точек зрения, за исключением только условия для проекций (Г.27). Бо-
лее конкретно это соображение можно сформулировать так: для заданной
структурированной системы из реконструктивного семейства следует выби-
рать такую обобщенную систему, которая опирается на всю информацию,
содержащуюся в этой структурированной системе, но только на эту инфор-
мацию. Такую обобщенную систему можно было бы назвать несмещенной
реконструкцией. Это система, реконструированная по структурированной
системе без смещений, то есть, с одной стороны, использующая всю имею-
щуюся информацию, а с другой, - не использующая никакой другой до-
полнительной информации.
Выбор несмещенной реконструкции, по существу, представляет собой
индуктивный вывод. Он может быть описан как следующая оптимизацион-
ная задача.
По заданной структурированной системе с поведением SF из множества
функций реконструктивного семейства
F
SF
выбрать такую функцию поведе-
ния
f
SF
, для которой мера нечеткости (шенноновская энтропия для вероятно-
стных систем или U-нечеткость для возможностных) была бы максимальной
при условии, что выполняются ограничения на проекции (Г.27).
Для вероятностных систем эта задача оптимизации фигурирует под на-
званием «принцип максимума энтропии».
Известно, что несмещенная реконструкция единственна и для вероятно-
стных, и для возможностных систем. Она определяет самое слабое из воз-
можных ограничений на переменные, соответствующие заданной структури-
рованной системе. Для возможностных систем
f
SF
это максимальное распре-
деление из реконструктивного семейства
F
SF
, или, другими словами, это рас-
пределение из множества распределений
F
SF
, которое представляет наиболь-
шее нечеткое подмножество всех полных состояний переменных систем.
Несмотря на то, что несмещенная реконструкция эпистемологически
наиболее существенна, поскольку она опирается на один-единственный хо-
рошо обоснованный принцип индуктивного вывода, для других целей могут
лучше подойти другие реконструкции. Совершенно естественным и важным
примером этого может послужить выбор обобщенной системы, для которой
минимизирована наибольшая возможная ошибка. Под ошибкой здесь имеет-
ся в виду расстояние между распределением (вероятностным или возможно-
стным) реконструированной обобщенной системы и распределением истин-
ной системы. Такого типа реконструкция - это реконструкция с наименьшим
риском. Конкретная формулировка полученной оптимизационной задачи за-
висит от того, какой тип расстояния используется. Особую важность из всех
268
возможных типов расстояния имеют те, что оценивают потерю информации.
Далее в этой главе, в особенности в разделах Г.7 и Г.9, мы рассмотрим такие
типы расстояний.
ПРОЦЕДУРЫ СОЕДИНЕНИЯ
Одним из важнейших результатов, связанных с задачей идентификации,
является то, что несмещенная реконструкция может быть определена с по-
мощью относительно простой процедуры, не включающей решение описан-
ной выше задачи оптимизации (задачи максимизации шенноновской энтро-
пии или U - нечеткости при заданных ограничениях). Эта процедура, назы-
ваемая процедурой соединения, основана на вероятностном или возможност-
ном варианте операции соединения довольно простым образом комбини-
рующей функции поведения элементов заданной структурированной систе-
мы.
Рассмотрим две функции поведения
],,[CB:f
],,[BA:f
10
10
2
1
→×
→
×
определенные на множествах состояний А, В, С, смысл которых мы поясним
ниже. Обратите внимание, что в множество В входит область определения
обеих функций. Соединение
1
f и
2
f, обозначаемое как
l
f *
2
f, это функция
],,[CBA:ff10
21
→
×
×
∗
свойства которой зависят от природы функций
1
f и
2
f . Если это функции рас-
пределения вероятностей, то
)],b|c(f),b,a(fmin[)c,b,a](ff[
2121
=
∗
(Г.33)
где
2
f(c|b) — условная вероятность с при .заданном b; если это функции рас-
пределения возможностей, то
)]c,b(f),b,a(fmin[)c,b,a](ff[
2121
=
∗
(Г.34)
Обратите внимание, что в отличие от (Г.33) в (Г.34) не используются ус-
ловные возможности. Дело в том, что тут используется соотношение
)],c,b(f),b,a(fmin[)b|с(f),b,a(fmin[
2121
=
которое легко может быть доказано.
Пусть операция соединения применяется к двум элементам структури-
рованной системы с выборочными переменными из множеств
1
S и
2
S и функ-
циями поведения
l
f и
2
f. Тогда необходимо преобразовать области определе-
ния функций
1
f и
2
f к виду А× В и В
×
С соответственно, где
А - множество совокупных состояний переменных, входящих только в
первый элемент, то есть переменных из множества
1
S - );SS(
21
∩
В - множество совокупных состояний переменных, входящих в оба эле-
мента, то есть переменных из
;SS
21
∩
С - множество совокупных состояний переменных, входящих только во
второй элемент, т. е. переменных из множества
2
S - )SS(
21
∩
.
269
Для определения несмещенной реконструкции данной струк-
турированной системы операция соединения должна быть выполнена для пар
элементов этой системы. При каждом ее выполнении два элемента сливаются
(объединяются) в один больший элемент новой структурированной системы.
Пусть операция соединения всегда выполняется в таком порядке, чтобы ре-
зультат ранее выполненных операций соединения входил в операцию соеди-
нения в качестве второго элемента. Эта процедура заканчивает свою работу
тогда, когда все элементы сливаются в одну обобщенную систему.
Будем называть эту процедуру базовой процедурой соединения. Прежде
чем ее формализовать, нужно рассмотреть два вырожденных случая, чтобы
все содержательные ситуации были описаны. В первом случае все перемен-
ные из первого элемента (соответствующего
1
f) могут быть включены во вто-
рой элемент (соответствующий
2
f). Это может быть, поскольку, вообще гово-
ря, второй элемент получен в результате выполнения неких операций соеди-
нения. В этом случае множество А является пустым, a
l
f принимает вырож-
денный вид
].,[B:f10
1
→
Во втором случае элементы не соединены. Это значит, что множество В
является пустым, а функции поведения имеют вырожденный вид
],,[A:f10
1
→
].,[B:f10
2
→
Обратите внимание на то, что вследствие требования неизбыточности
для структурированных систем (смотри раздел Г.3) и договоренности о том,
что результат предшествующих операций соединения всегда выступает как
2
f, множество С не может быть пустым. Для вероятностных систем вырож-
денные операции соединения определяются так:
)b|c(f)b(f)c,b](ff[
2121
⋅
=
∗
(Г.35)
для А=0 и
)c(f)a(f)c,a](ff[
2121
⋅
=
∗
(Г.36)
для В=0; для возможностных систем они определяются следующим образом:
)],c,b(f),b(fmin[)c,b](ff[
2121
=
∗
(Г.37)
)].c(f),a(fmin[)c,a](ff[
2121
=
∗
(Г.38)
Через
l
f *
2
f будем обозначать в зависимости от контекста как обычную,
так и вырожденную операцию соединения. Тогда базовая процедура соеди-
нения описывается следующим алгоритмом.
Базовая процедура соединения. Дана локально согласованная структури-
рованная система с поведением SF (вероятностная или возможностная) с
функциями поведения
x
f (x∈ N
q
). Для определения соединения
x
f для всех
x∈N
q
:
1) положить k=2 и
f =
1
f ;
2) произвести соответствующую группировку аргументов
k
f и f и выпол-
нить соответствующий вариант операции соединения
fff
k
→∗ (операция
может быть вероятностной или возможностной, обычной или вырожденной);
270
3) если k < q, то k+1 → k и перейти на шаг 2;
4) стоп.
Можно доказать следующее утверждение: если базовая процедура со-
единения применяется к согласованной возможностной системе SF, то в ре-
зультате всегда получается несмещенная реконструкция
f
SF
(максимальное
для реконструктивного семейства
F
SF
распределение возможностей). Однако
если эта процедура применяется к вероятностной системе, то несмещенная
(максимум энтропии) реконструкция получается только для определенного
класса структурированных систем — так называемых ациклических структу-
рированных систем, описываемых в разделе Г.7.
По полученному результату, не определяя типа данной струк-
турированной системы можно определить результат применения базовой
процедуры соединения
f несмещенную реконструкцию или нет. Если f удов-
летворяет условию для проекции
f]Sf[
xx
=↓
для всех
x∈N
q
, то это несмещенная реконструкция, в противном случае f не
соответствует данной структурированной системе и должна быть уточнена с
помощью следующей итеративной процедуры соединения.
Итеративная процедура соединения. Дана локально согласованная
структурированная система с поведением SF с вероятностными функциями
поведения
j
f (j∈N
0
,
q-1
). Дана также функция f, полученная с помощью базовой
процедуры соединения, примененной к SF, и число ∆
∈
[0, 1]; требуется с
точностью до ∆ определить функцию поведения несмещенной реконструк-
ции:
1) присвоить j=0, i=1 и
f
0
= f;
2) сделать соответствующее разбиение аргументов
j
f и f
i-1
и выполнить
операцию соединения
ii
j
f
~
ff →∗
−1
для вырожденного вида (Г.35);
3) если i ≠ 0 (mod q), то i + 1 → i, j+1 (mod q) → j, и перейти на 2;
4) если |
)c(f
~
)c(f
qii −
− | >∆ для какого-то с
∈
С, то i+1→ i, j+1 (mod q)→ j,
и перейти на 2;
5) конец.
Если после выполнения итеративной процедуры соединения
∑
=
c
i
)c(f1, то
∆
∆
+
≤
≥
−
)c(f)c(f)c(f
SF
i
SF
для всех
C
c ∈ ; в противном случае данная структурированная система SF
глобально не согласована (смотри раздел Г.11) и реконструкции SF не суще-
ствует, то eсть F
SF
= 0, и, следовательно, SF бессодержательна.
Пример Г.16. Рассмотрим структурированную систему из примера Г.11,
определенную в таблице Г.3. Сначала используем для определения несме-
щенной реконструкции вероятностный вариант базовой процедуры соедине-
ния. В первых столбцах таблице Г.10 приводятся промежуточный результат
2
f*
1
f и окончательный результат f =
3
f*(
2
f*
1
f). Легко видеть, что окончатель-
ный результат
f не соответствует заданной структурированной системе. Так,
