Миронов С.В., Пищухин А.М. Метасистемный подход в управлении

Подождите немного. Документ загружается.

311

тельности могут базироваться на укрупнении, а не на уточнении и тому

подобное. Одна из последовательностей должна выполняться по умолча-

нию, например простая последовательность, основанная на RС-процедуре.

Помимо своей основной роли при анализе систем естественного происхо-

ждения, реконструктивный анализ может быть применен также и для реше-

ния задач, связанных с искусственными системами. Понятие структурного

соседства можно, например, Непосредственно использовать для обнаруже-

ния дефектов в связях между элементами структурированной системы в

тех случаях, когда непосредственное наблюдение связей невозможно. Пра-

вильно использованное, оно может оказать большую помощь и при про-

ектировании. Его, например, можно применять для определения всего мно-

жества структурных уточнений, полностью сохраняющих данную проекти-

руемую систему с поведением. Такие уточнения являются основой для есте-

ственного способа проектирования по частям, что делает этот процесс бо-

лее управляемым. Под «естественным» здесь понимается то, что эти уточ-

нения содержат только входные и выходные переменные, входящие в дан-

ную систему с поведением, т. е. не содержат дополнительных (или искусст-

венных) переменных, вводимых на данном этапе. В каждом уточнении по

крайней мере некоторые из заданных переменных входят в несколько под-

систем и, следовательно, играют несколько разных ролей. В максимально

подробных уточнениях множественность использования любой переменной

достигает предела. Далее переменные должны при необходимости вво-

диться с помощью обычных методов декомпозиции или другого подходящего

метода проектирования.

Несмотря на такое использование реконструктивного анализа для ис-

кусственных систем, необходимо подчеркнуть, что основным его назначе-

нием является исследование естественных систем. Дело в том, что отноше-

ние часть-целое в естественных системах куда более неопределенно, чем в

естественных. Так, например, любая искусственная система является также

определением соответствующей обобщенной системы. Это непосредст-

венно следует из того факта, что соединяющие переменные в любой искусст-

венной системе являются либо переменными, которые прямо представляют

единственную систему с поведением (определенную в задаче проектиро-

вания), либo искусственными соединяющими переменными, введенными

только для косвенного представления этой единственной системы. Следова-

тельно, реконструктивное семейство любой искусственной структуриро-

ванной системы является единственным и представляет собой объединение

функций поведения ее элементов. То есть обобщенная система любой ис-

кусственной структурированной системы всегда представляется несмещен-

ной реконструкцией этой структурированной системы.

Это взаимно однозначное соответствие между искусственными структу-

рированными системами и связанными с ними обобщенными системами

является, без сомнения, доводом, возможно самым главным, в пользу того,

что связь между сопоставимыми системами с поведением и структурирован-

ными системами при исследовании систем (то есть при исследовании ес-

312

тественных систем) часто недостаточно хорошо понимается, особенно

людьми с инженерной подготовкой. В самом деле, в литературе описано

множество больших систем, которые, как предполагается, описывают раз-

личные естественные явления и составлены из меньших взаимосвязанных

систем (подсистем). На основании полученной конкретной

структурированной системы делаются выводы о свойствах обобщенной

системы так же, как это делается для аналогичных искусственных систем, т.

е. с помощью соединения или композиции функций поведения

соответствующих элементов. Понятно, что подобные выводы

основываются на предположении, что структурированные системы

представляют эту обобщенную систему точно так же, как для искусственных

систем. Это недоказанное и обычно неверное предположение, которое в

подобных исследованиях никогда явно не декларируется, принимается без

доказательства из-за неправомерной и сбивающей с толку аналогии с

искусственными системами.

Г.9. Вычислительные эксперименты

Эксперименты на компьютере не только воз-

можны, но и могут дать информацию,

которую невозможно получить иным пу-

тем.

У. Росс Эшби

В этом разделе в качестве примера метаметодологических средств

УРСЗ описываются вычислительные эксперименты, с помощью которых

можно определить некоторые важнейшие характеристики анализа реконст-

руируемости (связанные с задачей реконструкции). Эти характеристики нуж-

ны для более глубокого понимания реконструктивного анализа, помощи

пользователям УРСЗ по применению реконструктивного анализа при обще-

системных исследованиях и оценки новых принципов, таких, как прин-

цип индуктивного вывода, рассматриваемый в разделе Г.10.

В типичном эксперименте реконструктивная гипотеза выбирается при

заданном числе переменных и мощностях их множеств состояний. Затем про-

цесс порождения данных с помощью этой гипотезы моделируется на компью-

тере. В большей части этих экспериментов порождается последовательность

из 2000 элементов данных. В соответствии с описанными выше правилами

анализ реконструируемости проводится на 10 разных сегментах этих по-

следовательностей, содержащих 10, 20, 40, 80, 160, 320, 640, 1000, 1500 и 2000

элементов данных. Полученные для каждого сегмента результаты затем сравни-

ваются с данной реконструктивной гипотезой.

Для заданного числа переменных и их множеств состояний порождается и

анализируется соответствующее число различных последовательностей данных.

Усредненные результаты этих экспериментов затем используются для определе-

ния различных характеристик. Эксперименты для простоты ограничиваются

только С-структурами. Они были проведены для множеств &

, &

и &

; для

313

каждого множества были соответствующим образом представлены все уровни

уточнения. Аналогичные эксперименты были проведены для множеств состоя-

ний одинаковой мощности (2, 3, 4 и 5) для всех рассматриваемых перемен-

ных, а также для определенных смесей разной мощности. Поскольку отличия пе-

ременных, описываемых масками и средами, которые для общесистемных иссле-

дований очень важны, собственно для реконструктивного анализа значения не

имеют, эксперименты проводились только для нейтральных систем без памяти.

Последовательности данных порождались с помощью генератора случай-

ных чисел в соответствии с конкретной вероятностной структурированной сис-

темой (представленной С-структурой). Затем они анализировались вероятност-

ным и возможностным методами. На самом деле одной из целей проведения

экспериментов было сравнение этих двух методов и определение их областей

применения.

На начальном этапе эксперимента было замечено, что возможностный ана-

лиз демонстрирует тенденцию к естественной классификации реконструктивных

гипотез на каждом уровне уточнения на хорошие и плохие гипотезы, т. е. на

гипотезы соответственно с малыми и большими расстояниями. Было также от-

мечено, что корректные гипотезы (то есть гипотезы, с помощью которых были

порождены анализируемые данные) часто не обладают наименьшим расстоя-

нием, но почти всегда принадлежат к хорошему кластеру. Исходя из этих на-

блюдений вероятностный и возможностный анализы проводились по

немного отличающимся правилам.

При вероятностном анализе любая порожденная последовательность дан-

ных анализируется на соответствующей решетке уточнения дважды с помощью

двух различных процедур поиска. Согласно первой процедуре на каждом уровне

уточнения уточняются только структуры с минимальным расстоянием. Со-

гласно второй процедуре уточняются все структуры, чьи расстояния не превы-

шают минимальное более чем на 100%. По каждой из процедур характеристики

вычисляются отдельно.

При возможностном анализе структуры на каждом уровне уточнения кла-

стеризуются на плохие и хорошие и далее уточняются только хорошие струк-

туры. Любая последовательность данных анализируется дважды с помощью

двух разных процедур кластеризации. Для описания этих процедур пусть

}Ni|)d,C{(R

rii

∈

обозначает множество всех С-структур С

, оцениваемых на определенном уровне

уточнения конкретного эксперимента, с их расстояниями d

. Пусть d

≤d

i+1

для

всех i

1−

∈

N и пусть

G={C

, . .., С

};

В= {С

с+1

с+2

, . . ., С

}

- соответственно кластеры хороших и плохих структур, где 1 ≤ c ≤ r (то есть

кластер G всегда непустой, в то время как кластер В в некоторых случаях

может быть пустым).

314

В первой процедуре кластеризации с определяется наименьшим значением

i, для которого разность d

- d

i-1

превышает среднюю разность в R для всех

i∈N

r-1

. To есть

−

≤−

−

для )d(Ni

=∈ и

−

>−

Будем называть эту процедуру кластеризацией по средней разности

или AD-кластеризацией (average difference).

Во второй процедуре кластеризации с определяется значением

∈

для которого выражение

∑∑

−+−

−

|ad||ad|(

достигает минимума, причем

∑

−

Эта процедура основана на естественном кластеризационном требова-

нии о том, что расстояния между кластерами должны быть велики, а рас-

стояния внутри кластеров малы; будем называть это кластеризацией по внут-

реннему и внешнему расстоянию или IOD-кластеризацией (от англ. Inside and

Outside Distance).

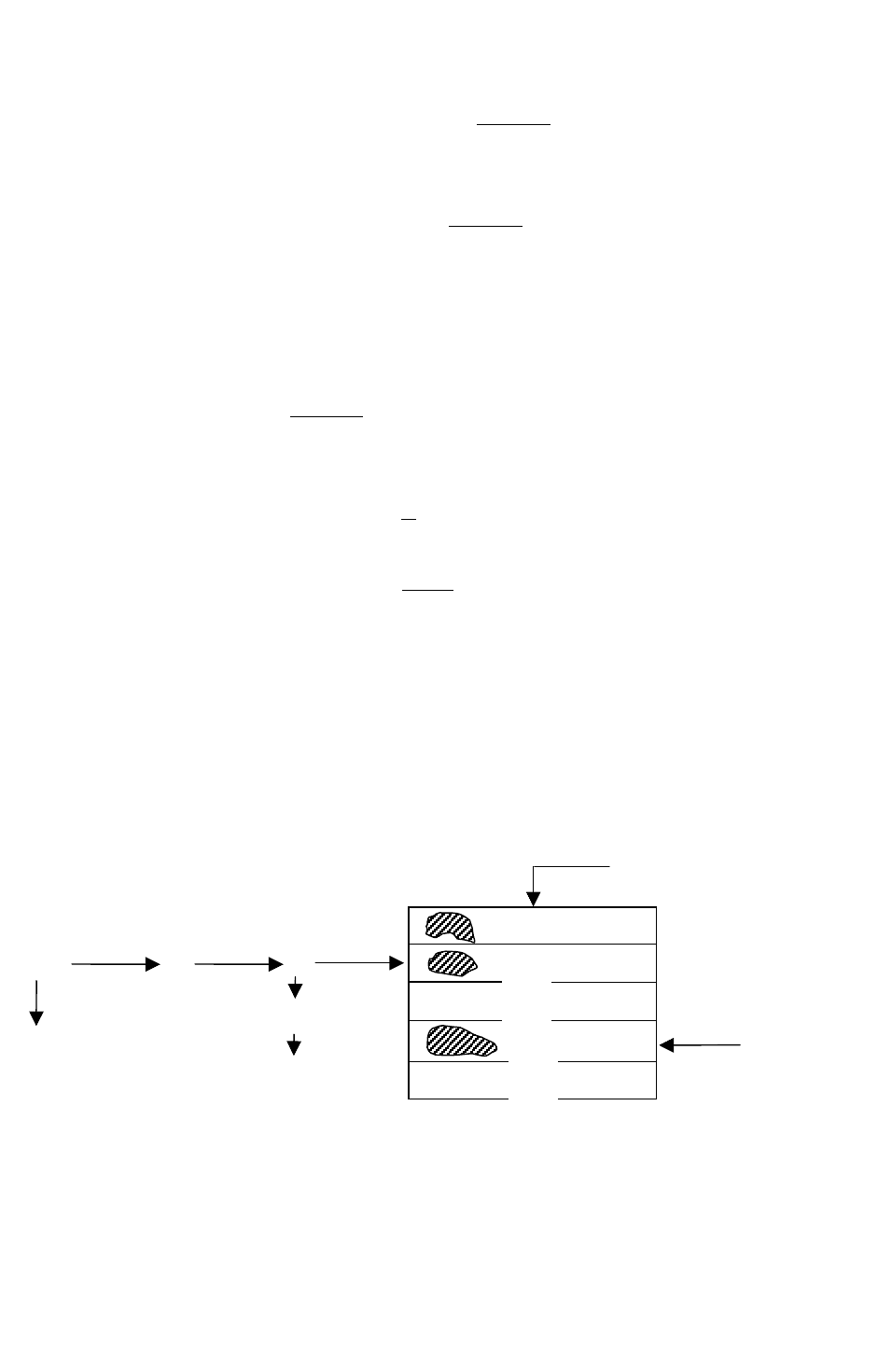
Теперь можно целиком описать процедуру реализации одного экспери-

мента (смотри диаграмму на рисунке Г.36). Она начинается с выбора струк-

турированной системы с поведением

SF (которая рассматривается в эксперимен-

те как подлинная). Эта система основывается на С-структуре. Эта структуризо-

ванная система, представляющая обобщенную систему с поведением

F (по-

лученную из системы

SF с помощью процедуры соединения), моделируется на

компьютере и используется для порождения данных. После порождения данных

из соответствующей системы данных D выводится обобщенная система с

поведением без памяти

F (вероятностная или возможностная). Затем для

цениваемые

структуры и

их расстояния

ровень

Рисунок Г.36 - Схема вычислительного эксперимента

315

ведением без памяти

F (вероятностная или возможностная). Затем для системы

F проводится реконструктивный анализ в соответствии с одной из упомянутых

выше процедур поиска (например, для возможностных систем, основанных на

одном из двух типов кластеризации). Результатом является последовательность

множеств С-структур (и их расстояний), которые оцениваются на отдельных

уровнях соответствующей решетки уточнения. Это множества, скажем мно-

жества

}Ii|)d,C{(E

lliil

∈

для l = 1, 2, ..., п(п — 1)/2, где п — число рассматриваемых переменных. Особый

интерес представляет множество E

для того же уровня уточнения, что и систе-

ма

SF. Система

F также используется для определения структурированной

системы

SF, основанной на такой же С-структуре, что и заданная структуриро-

ванная система

SF. Эта система (

SF) представляет обобщенную систему с

поведением

F (реконструированную обобщенную систему).

По множеству E

(l ∈N

n(n-1)/2

) и обобщенным системам с поведением

F, полученным в результате экспериментов одного типа (то есть для опреде-

ленного числа переменных, определенных множеств состояний, для вероятност-

ного или возможностного варианта и так далее), можно определить различные

характеристики результатов анализа реконструируемости. Опишем эти характе-

ристики на нескольких примерах систем из трех переменных. Некоторые ос-

новные характеристики для вероятностных систем (с тремя переменными)

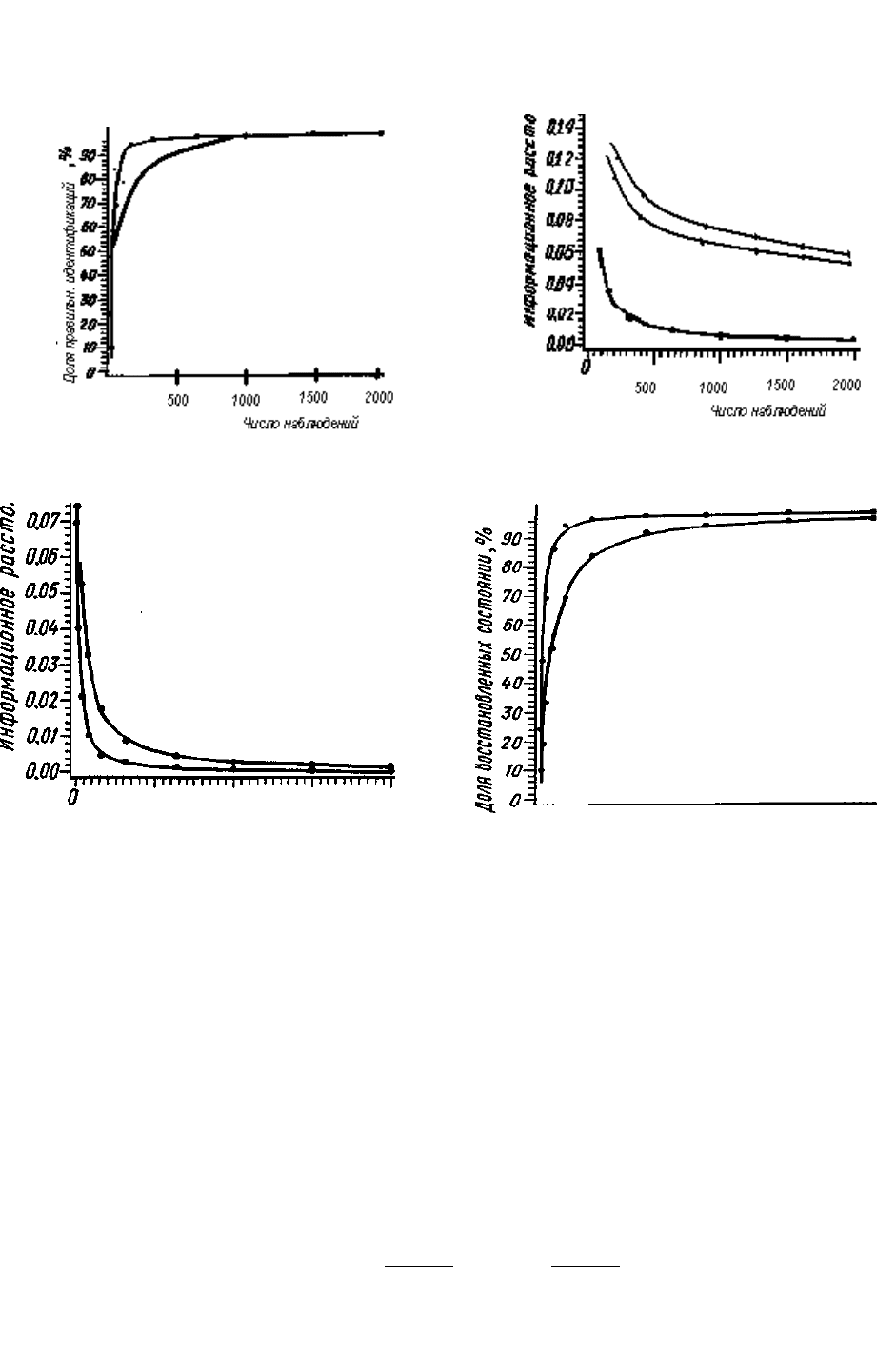
представлены на рисунке Г.37.

Они получены с использованием процедуры поиска, в которой уточняются

только структуры с минимальным расстоянием. Графики на рисунке Г.37,а опи-

сывают влияние числа наблюдений (объем данных |d|) на качество анализа

реконструируемости для переменных с двумя и с пятью состояниями. Качество

оценивается как для тех экспериментов, для которых процедура поиска полу-

чает на соответствующем уровне уточнения корректную структуру, являю-

щуюся структурой с наименьшим расстоянием. Как видно, 100%-ое качество

достигается достаточно быстро для обоих случаев. Несмотря на то, что с ростом

числа наблюдений результативность сходится к 100% во всех исследованных

случаях, скорость сходимости несколько падает с ростом числа переменных.

Это объясняется прежде всего высокой селективностью используемой процедуры

поиска. Видно также, что переменные с пятью состояниями (верхний график)

оцениваются лучше, чем переменные с двумя состояниями (нижний график).

Это также общая тенденция: с ростом мощностей множеств рассматриваемых со-

стояний улучшается и качество. Таким образом, для любого конкретного числа

переменных характеристики представленных систем с двоичными пере менны-

ми могут рассматриваться как худший случай.

На остальных графиках на рисунка Г.37 показаны характеристики анализа

реконструируемости только для двоичных переменных. На графике (рисунок

Г.37,б) показано, насколько отличается корректная структура по информаци-

онному расстоянию от других структур на том же уровне уточнения. На ниж-

нем графике представлено расстояние для корректной структуры D(

f ), на

316

среднем — наименьшие расстояния для структур, конкурирующих с коррект-

ной на том же уровне уточнения, и на верхнем средние расстояния для всех

структур, конкурирующих с корректной (в соответствии с процедурой по

а) б)

в) г)

Рисунок Г.37 - Некоторые характеристики анализа реконструируемо-

сти для вероятностных систем

иска) на одном уровне уточнения. Несмотря на то, что на вид этих кривых

влияет число переменных и мощность множеств их состояний, а также ис-

пользуемый тип расстояния, с ростом числа наблюдений эти расстояния все-

гда убывают, а расстояние для корректной структуры стремится к нулю.

На графике (рисунок Г.37в) сравниваются информационные расстояния

между подлинной системой

F и соответственно системами

F и

F. Поскольку

соответствующие пары распределений вероятностей

f и

f являются произ-

вольными, необходима общая мера информационного расстояния. Это расстоя-

ние, назовем его G, определяется формулой

,f(D)

,f(D)f,f(G

121

(Г.44)

где

f и

f - произвольные распределения вероятностей, определенные на одном и

том же конечном множестве состояний; D — специальное информационное рас-

317

стояние, заданное уравнением (Г.40); (

f +

f )/2—распределение вероятно-

стей, полученное взятием среднего для каждой пары соответствующих ве-

роятностей из

f и

f. Нижний график на рисунке Г.37,в представляет D(

f),а

а) б)

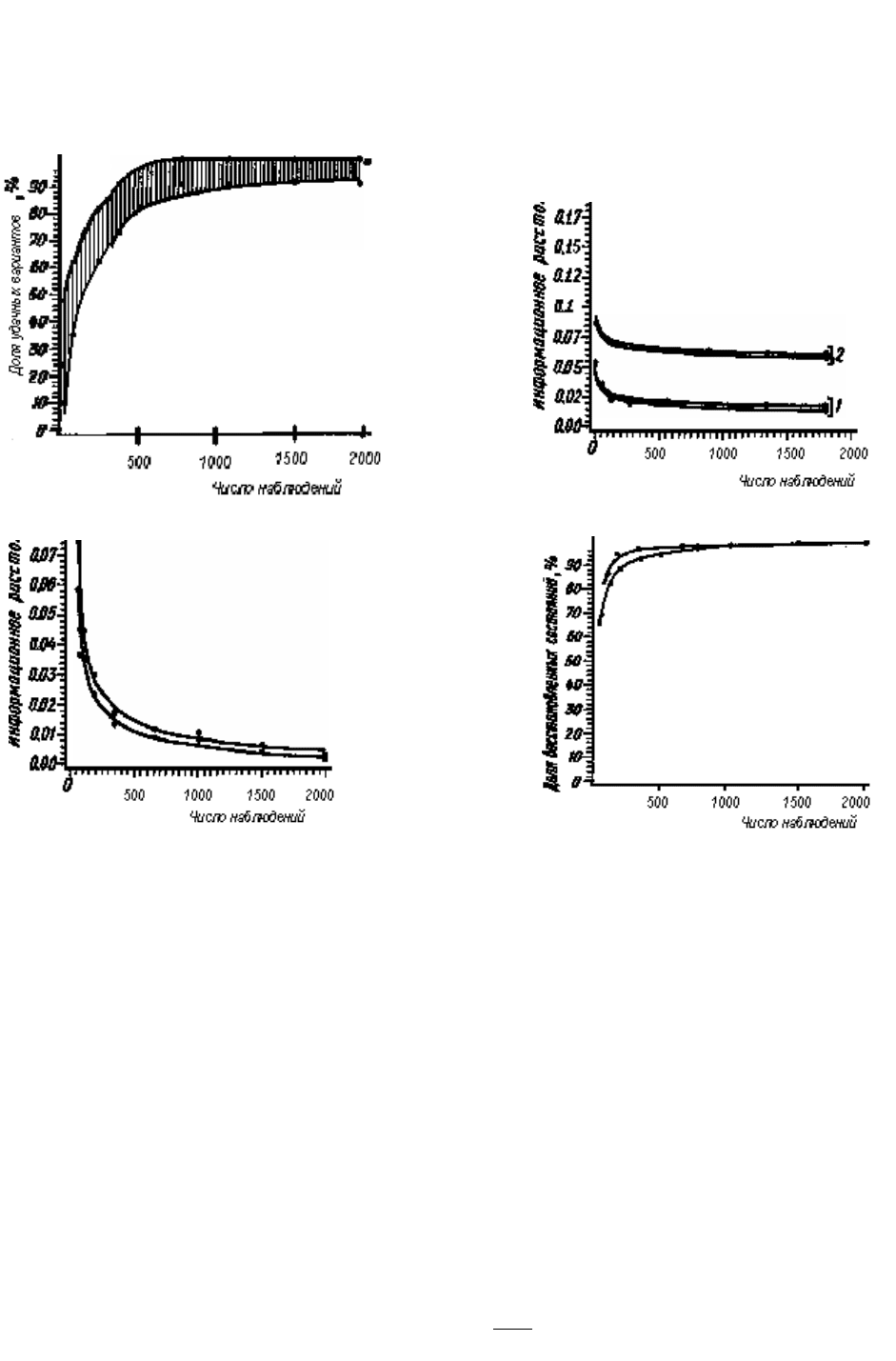
в) г)

Рисунок 7.38 - Некоторые характеристики анализа реконструируемости

для возможностных систем

верхний - D(

f). Таким образом, реконструированная система

F оказыва-

ется ближе к подлинной системе

F, чем система

F, опирающаяся только

на доступные данные. Это довольно неожиданный результат, важность которо-

го будет проанализирована в разделе Г.10.

На графиках (рисунок Г.37г) показана взаимосвязь множеств состояний с

ненулевыми вероятностями для трех участвующих в вычислительном экспери-

менте систем с поведением

F и

F; будем эти множества состояний обо-

значать соответственно

Х,

X и

Х. На нижнем графике показана доля тех со-

стояний

F, которые имеются в

F (это происходит из-за недостатка дан-

ных), то есть (

X)·100; на верхнем графике представлен процент со-

стояний

F, имеющихся в

100⋅

318

Из этих графиков ясно видно, что

XXX

TRD

⊆⊆ (Г.45)

Это столь же важное свойство, как и то, что получено из графиков на ри-

сунке Г.37,г, и оно также будет рассмотрено в разделе Г.10.

Возможностные аналоги описанных характеристик приведены на ри-

сунке Г.38. Они основаны на IOD-кластеризации. Поскольку реконструктив-

ный анализ возможностных систем основывается на работе с кластерами

структур, а не с отдельными структурами, то соответствие между вероят-

ностными характеристиками и их возможностными аналогами не является

прямым.

На рисунке Г.38 (а) показано качество возможностного анализа реконст-

руируемости для различных множеств состояний (от двух до пяти для пе-

ременной). График в данном случае имеет обобщенный вид, поскольку раз-

личия для разных множеств состояний малы и никаких особых тенденций вы-

явить не удается. Качество представляется как доля экспериментов, в которых

корректные структуры входят в кластер хороших структур. Остальные зави-

симости на рисунке Г.38 построены только для двоичных переменных

На рисунке Г.38,г показаны верхнее и нижнее информационные расстоя-

ния для двух кластеров структур. Они существенно отличаются от своих

вероятностных аналогов. Напротив, на рис. Г.38,в и г очень похожи на

свои вероятностные аналоги. Возможностная версия общего информационно-

го расстояния, использованная при построении графиков на этих рисунках,

определяется формулой

f)=D(

f V

f)+D(

f V

f),

(Г.46)

где

f и

f— произвольные распределения возможностей, определенные на од-

ном и том же конечном множестве состояний; D - специальное информацион-

ное расстояние, определяемое уравнением (Г.42);

f V

f - распределение

возможностей, получаемое взятием максимума для каждой пары

соответствующих возможностей из

f и

f .

Все эксперименты, для которых определялись данные характеристики,

проводились в предположении, что данные порождены некой структури-

рованной системой. Целью этих экспериментов было определение того,

насколько недостаток данных влияет на качество анализа реконструируе-

мости. Несмотря на то, что эти идеализированные эксперименты доста-

точно ценны и представляют собой естественный первый этап анализа ре-

конструируемости, очень желательно было бы расширить их для более об-

щих и более реальных ситуаций. Позвольте в качестве примера описать

обобщенные эксперименты, подготавливаемые в настоящее время. Подобно

идеализированным вычислительным экспериментам, обобщенные экспери-

менты будут также разбиты на группы по числу переменных и по мощно-

стям их множеств состояний. Для каждого эксперимента будет выбрано

определенное распределение, где для каждого обобщенного состояния

рассматриваемых переменных будет определено число его наблюдений. Одни

319

сматриваемых переменных будет определено число его наблюдений. Одни

распределения будут выбраны из различных архивов данных и из литерату-

ры, а другие — порождены случайными процессами. Эти два класса экспе-

риментов будут анализироваться по отдельности для того, чтобы понять,

обладают ли распределения, основанные на реальных данных, некими осо-

быми реконструктивными свойствами по сравнению с порожденными слу-

чайно распределениями.

Каждое отобранное распределение будет использовано двояко. Во-

первых, его реконструктивные свойства будут анализироваться как вероят-

ностным, так и возможностным методами. Во-вторых, оно будет использо-

вано для порождения данных, обычно для 2000 наблюдений. Затем распреде-

ления, полученные для различных сегментов данных, будут анализировать-

ся точно так же, как и исходные (истинные) распределения, и с помощью тех

же методов (вероятностного и возможностного). Наконец, результаты соот-

ветствующих экспериментов, полученные для различных сегментов данных,

будут сравниваться с теоретическими свойствами, определенными для исход-

ного распределения. Это сравнение будет проводиться для того, чтобы опре-

делить, насколько хорошо эти теоретические (истинные) свойства согласу-

ются с экспериментальными. Для каждого свойства, считающегося сущест-

венным, в результате выполнения каждой группы экспериментов будет опре-

делена зависимость средней сохранности этого свойства (а также вариа-

ции этой сохранности) от размеря анализируемого сегмента данных и ис-

пользуемого метода.

Вычислительные эксперименты так, как они описаны в этом разделе

для анализа реконструируемости, являются важнейшим инструментом для

метаметодологических исследований в науке о системах. УРСЗ должен

не только предоставлять в распоряжение пользователя метод решения

разных типов задач, но и давать метаметодологическое описание этих ме-

тодов. Характеристики анализа реконструируемости, описанные в данном

разделе,— это простой пример такого метаметодологического описания.

Г.10 Индуктивное рассуждение

Откуда берутся гипотезы, если они не ро-

ждаются прямо из головы Зевса? Частично

ответ состоит в том, что они возникают в

процессе порождения гипотез.

Герберт А. Саймон

Хотя индуктивное рассуждение неявно применялось только при решении за-

дач идентификации и реконструкции, оно используется практически в любой за-

даче, связанной с применением метода открытия в исследовании систем. Поэто-

му желательно дать обзор вопросов, связанных с индуктивными рассуждения-

ми, и это - одна из задач данного раздела; вторая задача - введение нового

320

принципа индуктивного вывода, основанного на некоторых особенностях анализа

реконструируемости.

Понятие индуктивного рассуждения мы будем рассматривать не в тра-

диционном узком смысле - как выведение общего заключения из частных приме-

ров, а более широко - как «охват всех недоказуемых случаев, в которых истин-

ность предпосылок хотя и не определяет инстинность заключения, но показыва-

ет, что есть серьезные основания доверять истинности этого заключения» (Фило-

софская энциклопедия).

Понятие индуктивного рассуждения в течение столетий являлось предме-

том философских споров, особенно после опубликования в 1739 г. Дейвидом

Хьюмом классического анализа этого понятия (David Hume, A. Treatise of Hu-

man Nature, William Collins, Glasgow, 1962). Несмотря на то, что было выдвину-

то множество доказательств, опровергающих скептическое отношение

Хьюма к возможности обоснования индуктивного вывода, в конечном счете

оказалось, что все эти доказательства имеют слабые места. В одних слу-

чаях доказательства оказывались несостоятельными из-за скрытой циклично-

сти (то есть из-за попыток обоснования индукции с помощью индукции), в дру-

гих - зависели от неких метафизических допущений (типа единообразия приро-

ды).

Основной недостаток этих доказательств заключается в том, что они

всерьез рассматривают тезис Хьюма как содержательную проблему. Альтерна-

тивный подход состоит в том, чтобы отказаться от попыток обоснования индук-

тивного вывода дедуктивными методами, что неявно присутствует в анализе

Хьюма, и рассматривать индуктивное рассуждение как процесс правильного

суждения на основе неполной информации. Одним из самых многообещающих

способов обоснования индуктивного рассуждения при таком подходе является

методологический прагматизм, предложенный недавно Решером [263]. Со-

гласно этому способу ключом к обоснованию индуктивного рассуждения яв-

ляются методы; понятно, что методологический прагматизм хорошо согласует-

ся с темой данной книги. Дадим краткий обзор основных особенностей этого

способа.

Решер рассматривает индуктивное рассуждение как метод «правильного

суждения с помощью систематизации на основе опыта, представляющего со-

бой оптимально правдоподобное сочетание догадки и имеющейся информа-

ции» [266]. Он утверждает, что информацию о природе можно получить,

только взаимодействуя с ней, и если мы не готовы довериться такому взаи-

модействию, то остается только отказаться от всего проекта исследования. Не-

смотря на то, что цели такого проекта являются как научными, так и

практическими, окончательная проверка должна основываться на том, насколь-

ко полученные знания оказываются полезны для деятельности человека.

Происходит это из-за того, что в отличие от теоретических построений на

практике для достижения целей (например, чтобы избежать гибели, травмы, бо-

лезни, страданий, огорчений и так далее) нужно принимать неотложные реше-

ния. В книге [260] подробно рассматривается вопрос о том, насколько необ-