Neamen D. Microelectronics: Circuit Analysis and Design

Подождите немного. Документ загружается.

708 Part 2 Analog Electronics

For the drain current to be independent of the drain-to-source voltage (for

λ = 0

), transistor M

should always be biased in the saturation region. The load

current is then

= K

− V

TN2

)

(10.42)

Substituting Equation (10.41) into (10.42), we have

= K





REF

TN1

− V

TN2



(10.43)

If M

and M

are identical transistors, then

TN1

= V

TN2

and

= K

, and Equa-

tion (10.43) becomes

= I

REF

(10.44)

Since there are no gate currents in MOSFETs, the induced load current is identi-

cal to the reference current, provided the two transistors are matched. The relationship

between the load current and the reference current changes if the width-to-length

ratios, or aspect ratios, of the two transistors change.

If the transistors are matched except for the aspect ratios, we ﬁnd

(W/L)

· I

REF

(10.45)

The ratio between the load and reference currents is directly proportional to the

aspect ratios and gives designers versatility in their circuit designs.

Output Resistance

The stability of the load current as a function of the drain-to-source voltage is an im-

portant consideration in many applications. The drain current versus drain-to-source

voltage is similar to the bipolar characteristic shown in Figure 10.4. Taking into ac-

count the ﬁnite output resistance of the transistors, we can write the load and refer-

ence currents as follows:

= K

− V

TN2

)

(1 + λ

DS2

)

(10.46(a))

and

REF

= K

− V

TN1

)

(1 + λ

DS1

)

(10.46(b))

Since transistors in the current mirror are processed on the same integrated

circuit, all physical parameters, such as V

, C

, and

, are essentially identical

for both devices. Therefore, taking the ratio of I

to I

REF

, we have

REF

(W/L)

(1 + λV

DS2

)

(1 + λV

DS1

)

(10.47)

Equation (10.47) again shows that the ratio I

REF

is a function of the aspect

ratios, which is controlled by the designer, and it is also a function of

and V

DS2

As before, the stability of the load current can be described in terms of the out-

put resistance. Note from the circuit in Figure 10.16 that

DS1

= V

GS1

constant for

a given reference current. Normally,

λV

DS1

= λV

GS1

 1

, and if (

W/L)

= (W/L)

then the change in bias current with respect to a change in V

DS2

≡

DS2

(10.48(a))

nea80644_ch10_687-752.qxd 6/19/09 4:27 AM Page 708 pmath DATA-DISK:Desktop Folder:18.6.09:MHDQ134-10:

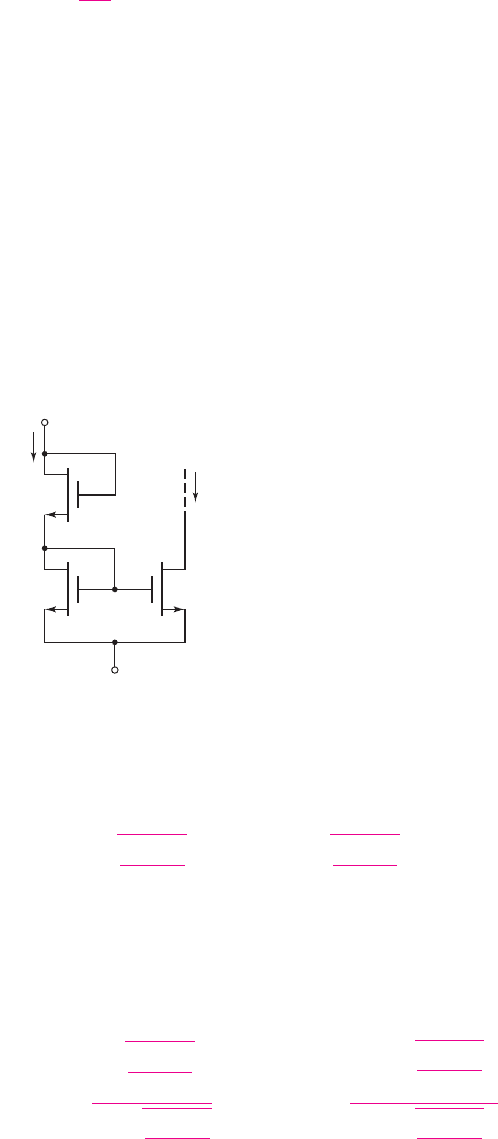
Chapter 10 Integrated Circuit Biasing and Active Loads 709

where

λI

(10.48(b))

where r

is the output resistance of the transistor. As we found with bipolar current-

source circuits, MOSFET current sources require a large output resistance for excel-

lent stability.

Reference Current

The reference current in bipolar current-source circuits is generally established by

the bias voltages and a resistor. Since MOSFETs can be conﬁgured to act like a

resistor, the reference current in MOSFET current mirrors is usually established by

using additional transistors.

Consider the current mirror shown in Figure 10.17. Transistors M

and M

are in

series; assuming

λ = 0

, we can write,

GS1

− V

TN1

)

= K

GS3

− V

TN3

)

(10.49)

= I

REF

–

––

GS1

–

GS3

GS2

Figure 10.17 MOSFET current source

If we again assume that

, μ

, and C

are identical in all transistors, then Equa-

tion (10.49) can be rewritten

GS1



(W/L)

· V

GS3



1 −



(W/L)



· V

(10.50)

where

is the threshold voltage of both transistors.

From the circuit, we see that

GS1

+ V

GS3

= V

− V

−

(10.51)

Therefore,

GS1



(W/L)

1 +



(W/L)

· (V

− V

−

) +



1 −



(W/L)





1 +



(W/L)



· V

= V

GS2

(10.52)

nea80644_ch10_687-752.qxd 6/19/09 4:27 AM Page 709 pmath DATA-DISK:Desktop Folder:18.6.09:MHDQ134-10:

710 Part 2 Analog Electronics

Finally, the load current, for

λ = 0

, is given by







GS2

− V

)

(10.53)

Since the designer has control over the width-to-length ratios of the transistors,

there is considerable ﬂexibility in the design of MOSFET current sources.

DESIGN EXAMPLE 10.8

Objective: Design a MOSFET current source circuit to meet a set of speciﬁcations.

Speciﬁcations: The circuit to be designed has the conﬁguration shown in Fig-

ure 10.17. The bias voltages are

= 2.5

V and

−

= 0

. Transistors are available

with parameters



= 100 μ

A/V

= 0.4

V, and

λ = 0

. Design the circuit such

that

REF

= 100 μ

= 60 μ

A, and

DS2

(

sat

)

= 0.4

Solution: We have

DS2

(

sat

)

= 0.4 = V

GS2

−0.4

, so that

GS2

= V

GS1

= 0.8

Then for transistor











GS2

− V

)



100



(0.8 − 0.4)

= 7.5

For transistor





REF







GS1

− V

)

100



100



(0.8 − 0.4)

= 12.5

The value of

GS3

is found as

GS3



− V

−



− V

GS1

= 2.5 −0.8 = 1.7V

Then for transistor

we ﬁnd





REF







GS3

− V

)

100



100



(1.7 − 0.4)

= 1.18

Trade-offs: As with other designs, slight variations in transistor parameters (



W/L

, and

)

will change the current values slightly. See Test Your Understanding

exercise TYU 10.5.

Comment: In this design, the output transistor remains biased in the saturation

region for

> V

(sat) = V

− V

= 0.8 −0.4 = 0.4V

Design Pointer: As with most design problems, there is not a unique solution.

The general design criterion was that M

was biased in the saturation region over a

wide range of

DS2

values. Letting

GS2

= 0.8

V was somewhat arbitrary. If

GS2

were smaller, the width-to-length ratios of M

and M

would need to be larger. Larger

values of

GS2

would result in smaller width-to-length ratios.

The value of

GS3

is the difference between the bias voltage and V

GS1

. If V

GS3

becomes too large, the ratio (W/L)

will become unreasonably small (much less

than 1). Two or more transistors in series can be used in place of M

to divide the

voltage in order to provide reasonable W/L ratios (see end-of-chapter problems).

nea80644_ch10_687-752.qxd 6/19/09 4:27 AM Page 710 pmath DATA-DISK:Desktop Folder:18.6.09:MHDQ134-10:

Chapter 10 Integrated Circuit Biasing and Active Loads 711

EXERCISE PROBLEM

Ex 10.8: For the circuit shown in Figure 10.17, the bias voltages are

= 1.8

V and

−

=−1.8

V, and the transistor parameters are

= 0.4



= 100 μ

A/V

and

λ = 0

. Design the circuit such that

REF

= 0.5

mA and

= 0.1

mA, and that

remains biased in the saturation region for

DS2

≥ 0.4

V. (Ans.

(

W/L

)

= 62.5

(

W/L

)

= 12.5

(

W/L

)

= 1.74)

Problem-Solving Technique: MOSFET Current-Source Circuit

1. Analyze the reference side of the circuit to determine gate-to-source voltages.

Using these gate-to-source voltages, determine the bias current in terms of

the reference current.

2. To ﬁnd the output resistance of the current source circuit, place a test voltage

at the output node and analyze the small-signal equivalent circuit. Keep in

mind that the reference current is a constant, which may make some of the

gate voltages constant or at ac ground.

Multi-MOSFET Current-Source Circuits

Cascode Current Mirror

In MOSFET current-source circuits, the output resistance is a measure of the stability

with respect to changes in the output voltage. This output resistance can be increased

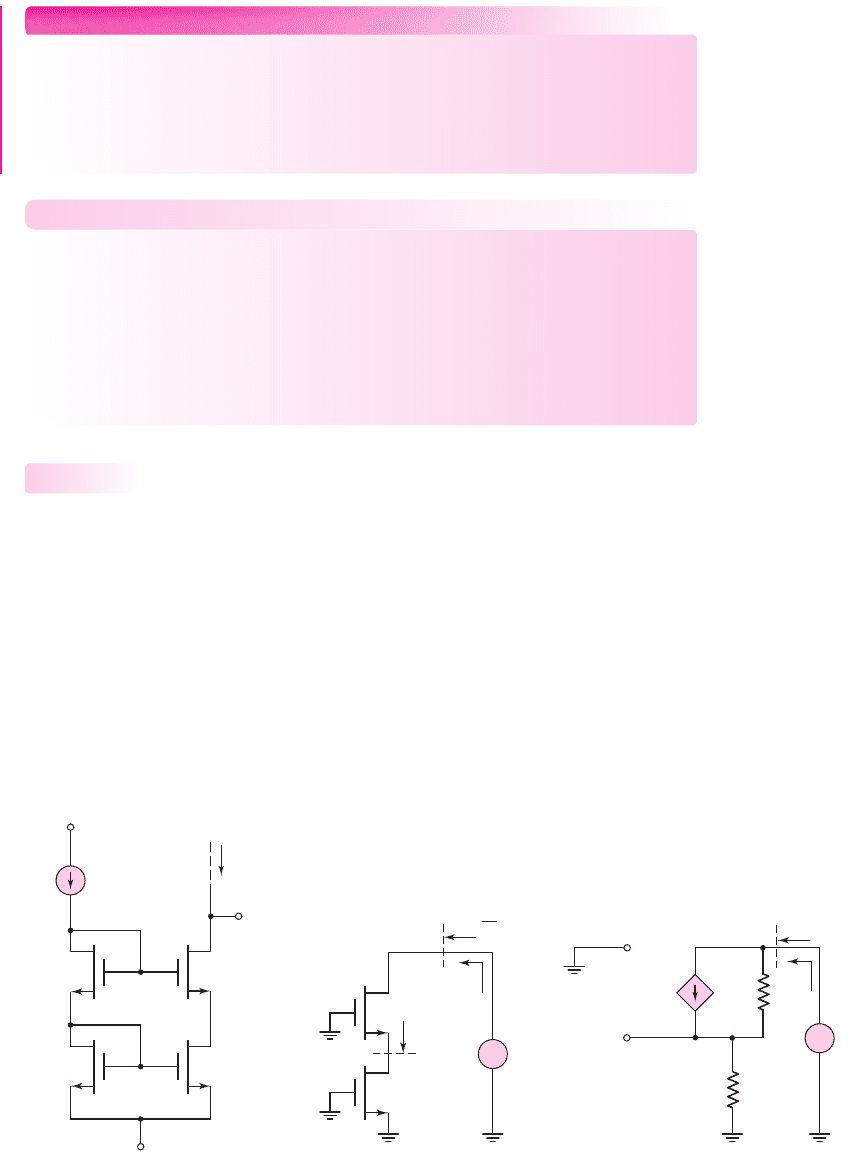
by modifying the circuit, as shown in Figure 10.18, which is a cascode current

mirror. The reference current is established by including another MOSFET in the

reference branch of the circuit as was done in the basic two-transistor current mirror.

Assuming all transistors are identical, then

= I

REF

To determine the output resistance at the drain of M

, we use the small-signal

equivalent circuit. Since I

REF

is a constant, the gate voltages to M

and M

, and

hence to M

and M

, are constant. This is equivalent to an ac short circuit. The ac

equivalent circuit for calculating the output resistance is shown in Figure 10.19(a).

10.2.2

REF

–

Figure 10.18 MOSFET cascode

current mirror

(a)

–

(b)

gs4

–

gs4

–

Figure 10.19 Equivalent circuits of the MOSFET cascode current mirror

for determining output resistance

nea80644_ch10_687-752.qxd 6/19/09 4:27 AM Page 711 pmath DATA-DISK:Desktop Folder:18.6.09:MHDQ134-10:

712 Part 2 Analog Electronics

The small-signal equivalent circuit is given in Figure 10.19(b). The small-signal

resistance looking into the drain of M

is r

Writing a KCL equation, in phasor form, at the output node, we have

= g

gs4

−(−V

gs4

)

(10.54)

Also,

gs4

=−I

(10.55)

Substituting Equation (10.55) into (10.54), we obtain

+ g

(10.56)

The output resistance is then

= r

(1 + g

)

(10.57)

Normally,

 1

, which implies that the output resistance of this cascode

conﬁguration is much larger than that of the basic two-transistor current source.

EXAMPLE 10.9

Objective: Compare the output resistance of the cascode MOSFET current source to

that of the two-transistor current source.

Consider the two-transistor current source in Figure 10.17 and the cascode

current source in Figure 10.18. Assume

REF

= I

= 100 μ

A in both circuits,

λ =

0.01 V

−1

for all transistors, and g

= 0.5 mA/V.

Solution: The output resistance of the two-transistor current source is, from Equa-

tion (10.48(b)),

λI

REF

(0.01)(0.10)

⇒ 1M

For the cascode circuit, we have

= r

= 1

M. Therefore, the output resistance

of the cascode circuit is, from Equation (10.57),

= r

(1 + g

) = 1 +(1)[1 +(0.5 × 10

−3

)(10

)]

= 502 M

Comment: The output resistance of the cascode current source is substantially

larger than that of the basic two-transistor circuit. Since

∝ 1/R

, the load

current in the cascode circuit is more stable against variations in output voltage.

Design Pointer: Achieving the output resistance of 502 M assumes the transistors

are ideal. In fact, small leakage currents will begin to be a factor in actual output

resistance values, so a value of 502 M may not be achieved in reality.

nea80644_ch10_687-752.qxd 6/19/09 4:27 AM Page 712 pmath DATA-DISK:Desktop Folder:18.6.09:MHDQ134-10:

Chapter 10 Integrated Circuit Biasing and Active Loads 713

EXERCISE PROBLEM

Ex 10.9: In the MOSFET cascode current source shown in Figure 10.18, all

transistors are identical, with parameters:

= 1

= 80 μ

A/V

, and

λ =

0.02 V

−1

. Let

REF

= 20 μ

A. The circuit is biased at

= 5

V and

−

=−5

Determine: (a) V

of each transistor, (b) the lowest possible voltage value V

, and

. (Ans. (a) V

1.5 V (b)

(min) =−3.0

V (c) R

505 M)

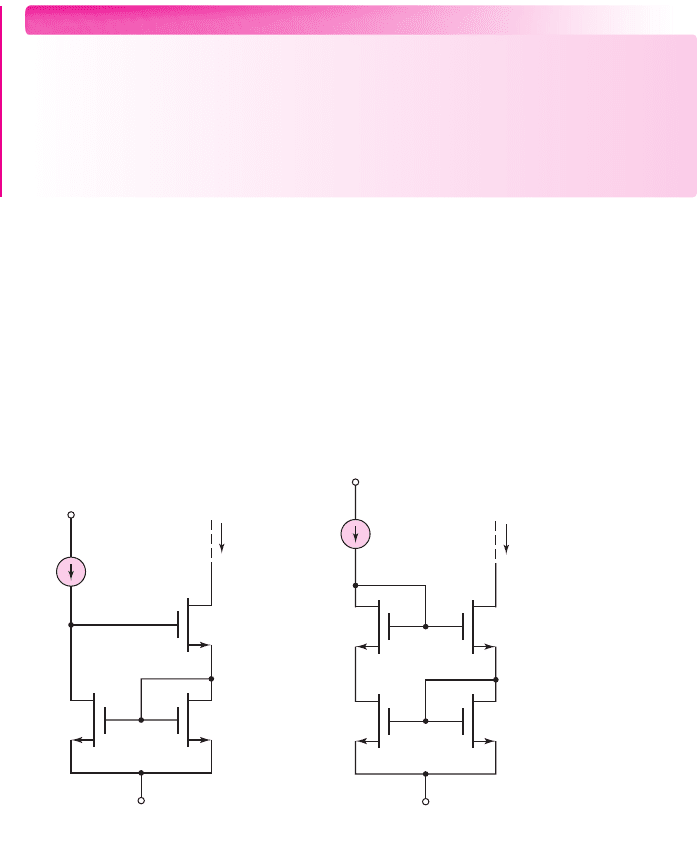
Wilson Current Mirror

Two additional multi-MOSFET current sources are shown in Figures 10.20(a) and

10.20(b). The circuit in Figure 10.20(a) is the Wilson current source. Note that the

values of M

and M

are not equal. Since

is not zero, the ratio I

REF

is slightly

different from the aspect ratios. This problem is solved in the modiﬁed Wilson

current source, shown in Figure 10.20(b), which includes transistor M

. For a con-

stant reference current, the drain-to-source voltages of M

, M

, and M

are held

constant. The primary advantage of these circuits is the increase in output resistance,

which further stabilizes the load current.

(a) (b)

REF

–

REF

–

Figure 10.20 (a) MOSFET Wilson current source and (b) modiﬁed MOSFET Wilson current

source

Wide-Swing Current Mirror

If we consider the cascode current mirror in Figure 10.18, we can determine the min-

imum value of V

, which will inﬂuence the maximum symmetrical swing of the

voltage in the load circuit being biased. The gate voltage of M

= V

−

+ V

GS1

+ V

GS3

(10.58)

The minimum V

is then

(min) = V

− V

GS4

+ V

DS4

(sat)

(10.59)

Assuming matched transistors,

GS1

= V

GS2

= V

GS4

≡ V

. We then ﬁnd

(min) = V

−

(

+ V

DS4

(sat)

)

(10.60)

nea80644_ch10_687-752.qxd 6/19/09 4:27 AM Page 713 pmath DATA-DISK:Desktop Folder:18.6.09:MHDQ134-10:

714 Part 2 Analog Electronics

In considering the simple two-transistor current mirror, the minimum output volt-

age is

(min) = V

−

+ V

(sat)

(10.61)

If, for example,

= 0.75

V and

= 0.50

V, then from Equation (10.60),

(min) = 1.0

V above

−

, and from Equation (10.61), V

(min) is only 0.25 V

above

−

. For bias voltages in the range of

±3.5

V, this additional required voltage

across the output of the cascode current mirror can have a signiﬁcant effect on the

output of the load circuit.

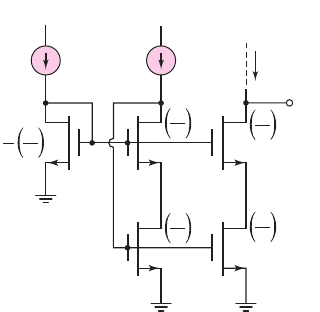
One current mirror circuit that does not limit the output voltage swing as

severely as the cascode circuit, but retains the high output resistance, is shown in Fig-

ure 10.21. Width-to-length ratios of the transistors are shown. Otherwise, the transis-

tors are assumed to be identical.

REF

Bias

REF

Figure 10.21 A wide-swing MOSFET cascode current mirror

The transistor pair M

and M

acts like a single diode-connected transistor in

creating the gate voltage for M

. By including M

, the drain-to-source voltage of M

is reduced and is matched to the drain-to-source voltage of M

. Since M

is one-

fourth the size of M

−M

and since all drain currents are equal, we have

GS5

− V

) = 2(V

GSi

− V

)

(10.62)

where

GSi

corresponds to the gate-to-source voltage of M

−

The voltage at the gate of M

= V

GS5

= (V

GS5

− V

) + V

(10.63)

The minimum output voltage at the drain of M

(min) = V

− V

GS1

+ V

DS1

(sat)

= [(V

GS5

− V

) + V

] − V

GS1

+(V

GS1

− V

)

(10.64)

(min) = V

GS5

− V

= 2(V

GSi

− V

) = 2V

DSi

(sat)

(10.65)

If we have

GSi

= 0.75

V and

= 0.5

V, then V

(min)

0.50 V, which is one-

half the value for the cascode circuit. At the same time, the high output resistance is

maintained.

nea80644_ch10_687-752.qxd 6/19/09 4:28 AM Page 714 pmath DATA-DISK:Desktop Folder:18.6.09:MHDQ134-10:

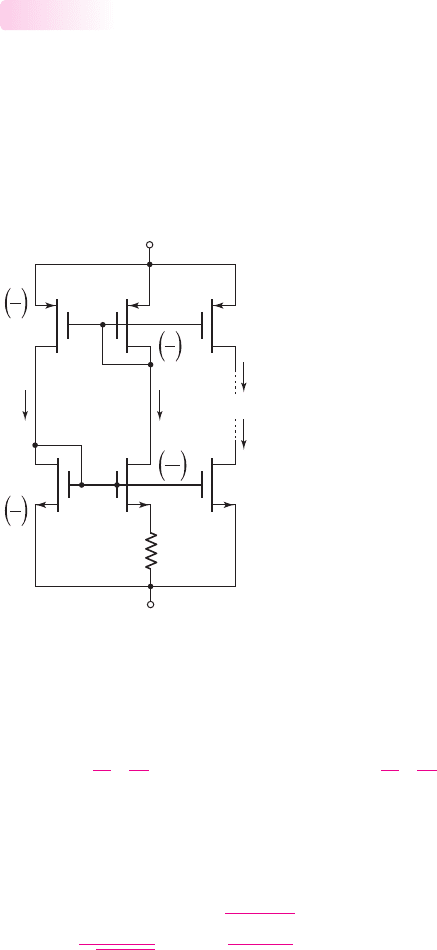
Chapter 10 Integrated Circuit Biasing and Active Loads 715

Discussion:

In the ideal circuit design in Figure 10.21, the transistors M

and M

are

biased exactly at the transition point between the saturation and non-saturation regions.

The analysis has neglected the body effect, so threshold voltages will not be exactly

equal. In an actual circuit design, therefore, the size of M

will be made slightly smaller

to ensure transistors are biased in the saturation region. This design change then means

that the minimum output voltage increases by perhaps 0.1 to 0.15 V.

Bias-Independent Current Source

In all of the current mirror circuits considered up to this point (both BJT and MOSFET),

the reference current is a function of the applied supply voltages. This implies that

the load current is also a function of the supply voltages. In most cases, the supply

voltage dependence is undesirable. Circuit designs exist in which the load currents

are essentially independent of the bias. One such MOSFET circuit is shown in Fig-

ure 10.22. The width-to-length ratios are given.

10.2.3

–

Figure 10.22 Bias-independent MOSFET current mirror

Since the PMOS devices are matched, the currents I

and I

must be equal.

Equating the currents in M

and M

, we ﬁnd







GS1

− V

)

= I







GS2

− V

)

(10.66)

Also

GS2

= V

GS1

− I

(10.67)

Substituting Equation (10.67) into Equation (10.66) and solving for R, we obtain

R =

√



1 −



(W/L)



(10.68)

This value of resistance R will establish the drain currents

= I

. These currents

establish the gate-to-source voltage across M

and source-to-gate voltage across M

nea80644_ch10_687-752.qxd 6/19/09 4:28 AM Page 715 pmath DATA-DISK:Desktop Folder:18.6.09:MHDQ134-10:

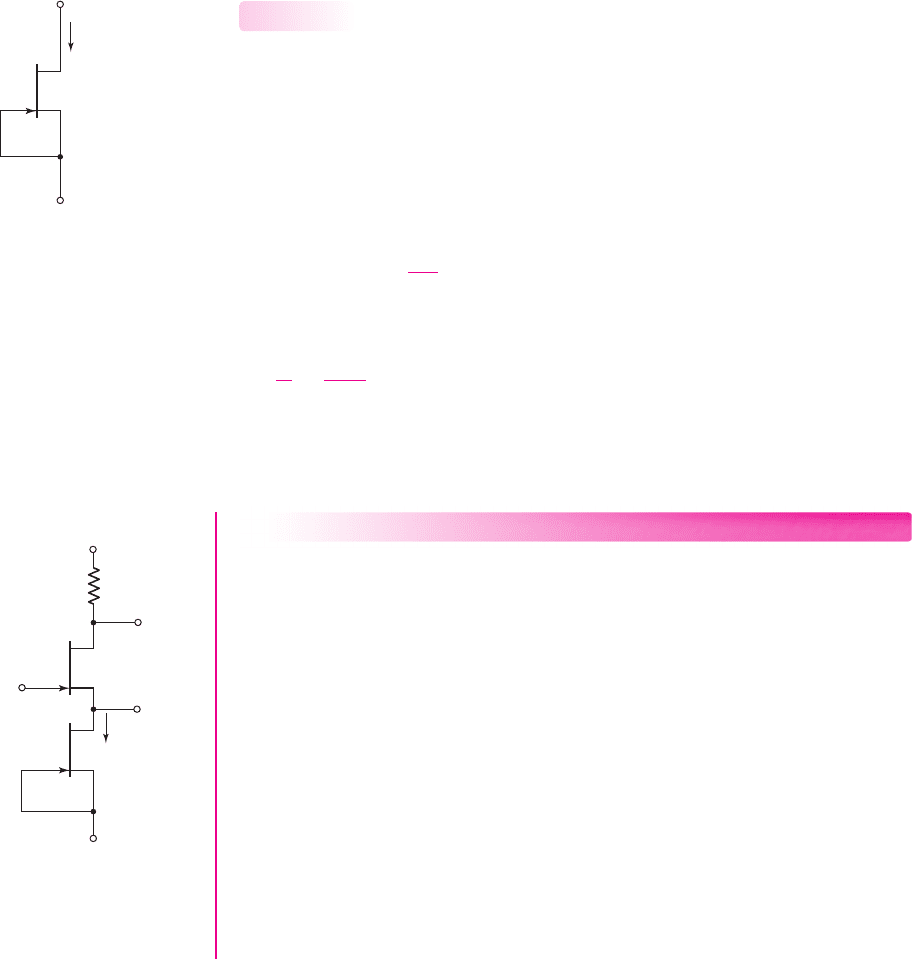
716 Part 2 Analog Electronics

These voltages, in turn, can be applied to M

and M

to establish load currents I

and I

The currents I

and I

are independent of the supply voltages

and

−

long as M

and M

are biased in the saturation region. As the difference,

− V

−

increases, the values of V

DS2

and V

SD3

increase but the currents remain essentially

constant.

Similar bipolar bias-independent current mirror designs exist, but will not be

covered here.

JFET Current Sources

Current sources are also fundamental elements in JFET integrated circuits. The simplest

method of forming a current source is to connect the gate and source terminals of a

depletion-mode JFET, as shown in Figure 10.23 for an n-channel device. The device

will remain biased in the saturation region as long as

≥ v

(sat) = v

− V

(10.69)

In the saturation region, the current is

= I

DSS



1 −



(1 + λv

) = I

DSS

(1 + λv

)

(10.70)

The output resistance looking into the drain is, from Equation (10.70),

= λI

DSS

(10.71)

This expression for the output resistance of a JFET current source is the same as

that of the MOSFET current source.

EXAMPLE 10.10

Objective: Determine the currents and voltages in a simple JFET circuit biased with

a constant-current source.

Consider the circuit shown in Figure 10.24. The transistor parameters are:

DSS1

= 2

mA,

DSS2

= 1

mA,

= V

=−1.5

V, and

= λ

= 0.05 V

−1

Determine the minimum values of V

and V

such that Q

is biased in the saturation

region. What is the value of I

Solution: In order for Q

to remain biased in the saturation region, we must have

≥

= 1.5V

, from Equation (10.69). The minimum value of V

is then

(min) − V

−

= v

(min) = 1.5V

(min) = 1.5 + V

−

= 1.5 +(−5) =−3.5V

From Equation (10.70), the output current is

= I

DSS2

(1 + λv

) = (1)[1 +(0.05)(1.5)] = 1.08 mA

10.2.4

–

Figure 10.23 Depletion-

mode JFET connected

as a current source

= 5 V

–

= –5 V

Figure 10.24 The dc

equivalent circuit of simple

JFET ampliﬁer biased

with JFET current source

nea80644_ch10_687-752.qxd 6/19/09 4:28 AM Page 716 pmath DATA-DISK:Desktop Folder:18.6.09:MHDQ134-10:

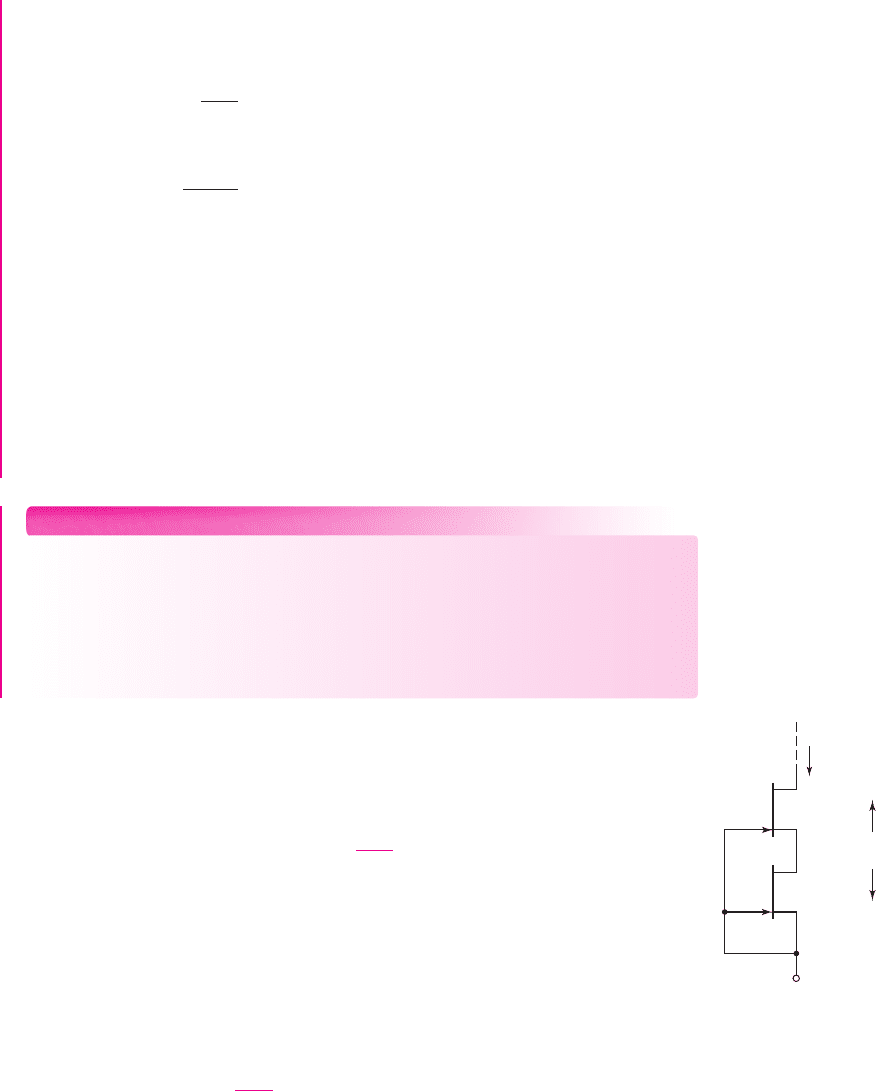
Chapter 10 Integrated Circuit Biasing and Active Loads 717

As a ﬁrst approximation in calculating the minimum value of V

, we neglect the

effect of

in transistor Q

. Then, assuming Q

is biased in the saturation region, we

have

= I

DSS1



1 −

GS1



1.08 = 2



1 −

GS1

(−1.5)



which yields

GS1

=−0.40 V

We see that

GS1

=−0.40 V = V

− V

= V

−(−3.5)

=−3.90 V

Comment: Since Q

is an n-channel device, the voltage at the gate is negative with

respect to the source.

EXERCISE PROBLEM

*Ex 10.10: Consider the JFET circuit in Figure 10.24. The transistor parameters

are:

DSS2

= 0.5

mA,

DSS1

= 0.8

mA,

= V

=−2

V, and

= λ

0.15 V

−1

. Determine the minimum values of V

and V

such that Q

is biased in

the saturation region. What is the value of I

? What is the output impedance look-

ing into the drain of Q

? (Ans.

(min) =−3

= 0.65

mA,

(min) =

−3.2

= 1.09



)

The output resistance of a JFET current source can be increased by using a cas-

code conﬁguration. A simple JFET cascode current source with two n-channel

depletion-mode devices is shown in Figure 10.25. The current–voltage relationship,

assuming Q

and Q

are identical, is given by

= I

DSS

(1 + λv

DS1

) = I

DSS



1 −

GS2



(1 + λv

DS2

)

(10.72)

From the circuit, we see that

GS2

=−v

DS1

. We deﬁne

= v

DS1

DS2

(10.73(a))

so that

DS2

= V

−v

DS1

(10.73(b))

From Equation (10.72), we obtain

(1 + λv

DS1

) =



1 +

DS1



[1 + λ(V

−v

DS1

)]

(10.74)

For a given application, the value of

will usually be known, and the value

DS1

can then be determined. The load current i

can then be calculated by using

Equation (10.72).

–

DS1

–

DS2

Figure 10.25 JFET

cascode current source

nea80644_ch10_687-752.qxd 6/19/09 4:28 AM Page 717 pmath DATA-DISK:Desktop Folder:18.6.09:MHDQ134-10: