Салимов Р.Б. Математика (для студентов бакалавриата)
Подождите немного. Документ загружается.


201
довательным дифференцированием по
x
. Приравняв коэффициенты при оди-
наковых степенях в правой и левой частях (26), получим систему уравне-
ний, содержащих искомые коэффициенты Этих уравнений будет
столько же, сколько имеется неизвестных коэффициентов. Из этой системы и
найдём все коэффициенты
Приведенные рассуждения можно рассматривать как нестрогое обоснова-
ние (24). Уравнения для нахождения вышеуказанных искомых коэффициен-
тов можно получить иначе, а именно, подставив в (26) вместо любые числа.
При каждой подстановке будем иметь определённое уравнение. В итоге по-
лучим число уравнений, равное числу неизвестных коэффициентов. На прак-
тике обычно два вышеуказанных подхода комбинируют. Отметим, что в (26)
вместо выгодно подставлять не любые значения, а значения, равные дей-
ствительным корням
Пример 1.
( )( )
3
33
11 11
x x AB C
x x xx x x x x
−−
= =++
− +− + −
(27)
( )( ) ( ) ( )
( )( )
3
11 1 1
3
.
11
Ax x Bxx Cxx
x
x x xx x
−++−++
−
=
− +−
(28)
( ) ( )
2
3.x xABC x BC A−= +++−+−
Приравняем коэффициенты при одинаковых степенях слева и справа и
получим систему уравнений
0 ;1 ; 3 .ABC BC A= + + =−+ −=−
Отсюда найдём Но проще эти коэффициенты найти из других уравне-
ний, которые получим, подставив в (28) вместо значения, равные корням
знаменателя:
1, 1.xx=−=
При этом будем иметь соответственно
3 , 4 2, 2 2.ABC−=− −= −=
Следовательно,
2, 1.BC=−=−
Таким обра-
зом, (27) примет вид
3
33 2 1
.
11
x
x xxx x
−
=−−
− +−
x
12
, , ,...AB B
12
, , ,...AB B
x
x
( )
.fx
( )( ) ( ) ( )
3 11 1 1x Ax x Bxx Cxx−= + −+ −+ +
x
,,.ABC
x
0,x =
3,A =
5354.ru
202
Пример 2.
Правую часть приведём к общему знаменателю, затем, отбросив общий зна-
менатель, получим
(29)
В (29) положим затем
2,x =
тогда
2
6 9,
2 / 3, 1.
3 3,
A
AB
B
−=
⇒=− =−
−=
Чтобы получить уравнение для , сравним коэффициент при слева и
справа в (29): Отсюда найдем
1
2/3.BA=−=
Окончательно будем
иметь
( )
( )
( )
2
32
5 221
.
3 4 3 13 2
2
x
xx x x
x
−
=−+ −
−+ + −
−
Пример 3.
Выражение в правой части приведём к общему знаменателю, затем отбросим
знаменатель. Тогда получим
(30)
Положим
1,x = −
затем Будем иметь при этом соответственно
12 2 ,
6, 2.
12 6 ,
A
AB
B
= −
⇒=− =
=
Ещё два уравнения для нахождения и получим, сравнив в (30) слева и
справа коэффициенты при и свободные члены:
Далее находим Таким образом,
(31)
( )( ) ( )
12
22
32
55
.
34 1 2
12 2
BB
x xA
xx x x
xx x
−−
= =++
−+ + −
+− −
( ) ( )( ) ( )
2
12
5 2 1 2 1.x Ax B x x B x−=⋅− +⋅+ −+ ⋅+
1,x = −
1
B
2
x
1
0.AB= +
( )( )
( )
43 2
2
12 12
.
1 11 1
11 1
A B Cx D
xxx x x xx
x x xx
+
= =++
+ −− + − ++
+ − ++
( )
( )
( )
( )
( )
( )
22 2
121111 1Ax xx Bx xx CxDx= − ++ + + ++ + + −
1.x =
C
D
3
x
0 , 12 4.ABC ABD C AB C= + + =−+ − ⇒ =−− ⇒ =
12 4.D AB=− −+=−
43 2
12 6 2 4 4
.
111 1
x
xxx x x xx
−−
=++
+ −− + − ++

203
§ 8. Интегрирование рациональных дробей
Дана рациональная дробь нужно найти от нее интеграл
Здесь нужно различать два случая:
• Дробь является правильной. Тогда разложим её на сумму
простейших дробей, и искомый интеграл будет равен сумме интегралов от
простейших дробей.
• Дробь является неправильной. Тогда запишем её в виде сум-
мы
( ) ( ) ( ) ( ) ( )
,Qx fx Mx Fx fx= +
где – многочлен, а – пра-
вильная рациональная дробь. Последнюю разложим на сумму простейших
дробей. После этого проинтегрируем.
Итак, интеграл от рациональной дроби всегда может быть вычислен.
Пример. Вычислить
Воспользуемся формулой (31). Тогда
2
2
6 2 44
11 1
1
6ln | 1| 2ln | 1| 4 .
1
x
J dx dx dx
x x xx
x
x x dx
xx
−
=−+ + =
+ − ++
−
=− ++ −+
++
∫ ∫∫
∫
Интеграл предлагается вычислить самим, использовав материал
§
5 настоящей главы.
§ 9. Интегрирование простейших иррациональных функций
Рациональная функция представляет собой отношение двух многочленов,
следовательно, она определяется формулой, содержащей конечное число че-
тырёх арифметических действий: сложение, вычитание, умножение и деле-
ние, выполненных над независимой переменной, постоянными и получаемы-
ми при этом выражениями.
Иррациональной называется функция, которая определяется формулой,
содержащей конечное число четырех арифметических действий и извлечение
корня с целым показателем, выполненных над независимой переменной, по-
стоянными и выражениями, представляющими рациональные функции от не-
зависимой переменной.
Рассмотрим интеграл
( ) ( )
,Qx f x
( ) ( )
[ / ].Q x f x dx
∫
( ) ( )
Qx f x
( ) ( )
Qx f x
( )
Mx
( ) ( )
Fx fx
43
12
.
1
J dx
xxx
=
+ −−
∫
2
1
4
1
x
dx
xx
−
++
∫

5354.ru
204
1111
, , ,... .
p
m
ax b ax b
J R x dx
ax b ax b
++
=
++
∫
– рациональная функция своих аргументов, , – заданные
действительные числа, причем показатели корней – целые числа. Под всеми
корнями стоит одно и то же выражение, в котором и числитель, и знаменатель
дробей подкоренного выражения содержат в первой степени. Пусть –
наименьшее общее кратное показателей корней , т. е. число, которое
делится без остатка на эти показатели. Чтобы избавиться от иррационально-
сти, сделаем замену
11
,
n
ax b
U
ax b
+
=
+
(32)
Следовательно,
'1
11
2
1
.
()
n
U
n
ab ba
dx x dU nU dU
a aU
−
−
= =
−
Тогда интеграл примет вид
( )
// 1
1 11
2
1
1
,,, .
n
nm np n
n
n
bU b ab ba
J R U U nU dU
a aU
a aU
−
−−
=
−
−
∫
Но числа суть целые
числа, так как по условию – наименьшее кратное чисел Под знаком
интеграла мы получим рациональную функцию, которая может быть проин-
тегрирована. В частности, если то подкоренное выражение и за-
мена (32) примут вид и соответственно.
Пример. Вычислить интеграл
Сделаем замену
2
4.xU+=
Тогда и
( )
23
2
4
2 2 4 24,
3
4
xU U
dx UdU U dU U C
U
x
−
= = − = −+
+
∫∫ ∫
здесь согласно замене
4.Ux
= +
§ 10. Интегрирование тригонометрических функций
Рассмотрим интеграл
( )
1
sin , cos ,J R x x dx=
∫
где – рациональная функция
своих аргументов. Покажем, что приводится к интегралу от рациональной
функции и может быть вычислен. Сделаем замену
(33)
При этом
/2 arctgxU=
, следовательно, поэтому
R
, ,...mp
11
,, ,aba b
x
n
, ,...mp
1
1
.
n
n
bU b
x
a aU
−
=
−
J
, ,...nm np
n
, ,...mp
1
0,a =
1
1,b =
ax b+
n
ax b U+=
.
4
x
dx
x+
∫
2
4,xU= −
2dx UdU=
R
1
J
tg( 2) .xU=
2arctg ,xU=

205
( )
2
2/ 1 .dx U dU
= +
(34)
Чтобы представить подынтегральную функцию через нужно и
выразить через т. е. через Известно, что
Эту формулу запишем так:
Числитель и знаменатель дроби в правой части разделим на и полу-
чим В силу (33) будем иметь
(35)
Аналогично поступим с
( ) ( ) ( ) ( )
22 22
cos [cos 2 sin 2 ]/[cos 2 sin 2 ].xx x x x=−+
И числитель, и знаменатель правой части последней формулы поделим на
тогда поэтому
(36)
Выражения (34) – (36) подставим в интеграл , который теперь примет вид
Здесь подинтегральная функция является уже ра-
циональной функцией от Вычислив , подставим в полученное выраже-
ние и вернёмся к исходной переменной.
Пример. Вычислить интеграл
Сделаем замену (33). Тогда и будут выражаться формулами (34),
(35), поэтому
2
2
2 (1 )
ln | | ln | tg( 2) | .
sin 2 (1 )
dx U dU
dU U c x C
x UU U
+
= = = += +
+
∫∫ ∫
Замена (33) при вычислении интегралов вида всегда приводит к успе-
ху, т. е. позволяет вычислить этот интеграл до конца. В связи с этим замену
(33) называют универсальной. В силу своей общности она не всегда является
выгодной, поэтому иногда лучше применять не (33), а другую замену. Отме-
тим три таких случая.
,U
sin x
cos x
,U
tg( 2).x
( ) ( )
sin 2sin 2 cos 2 .xxx=
( ) ( ) ( ) ( )
22
sin 2sin 2 cos 2 /[sin 2 cos 2 ].xxx x x= +
( )
2
cos 2x
( )
( )
2
sin [2tg 2 ]/[1 tg 2 ].xx x= +
2
sin 2 /(1 ).xU U= +
cos :x
( ) ( )
22
cos cos 2 sin 2 ,xx x= −
( )
2
cos 2 ,x
( ) ( )
22
cos [1 tg 2 ]/[1 tg 2 ],xx x=−+
22
cos (1 ) /(1 ).xU U=−+
1
J
2
1
222
21 2
,.
111
U U dU
JR
UUU
−
=
+++
∫
.U
1
J
tg( 2)Ux=
sin .dx x
∫
sin x
dx
1
J

5354.ru
206
1. Здесь лучше сделать замену тогда
и интеграл примет вид
2. Здесь надо взять тогда исходный интеграл при-
мет вид
( )( )
.R U dU−
∫
3.
( )
22
cos , sin ,R x x dx
∫
здесь и входят только в чётных степенях.
Сделаем замену тогда
Следовательно,
22
cos 1/(1 )
xU
= +
и Поэтому рассматриваемый
интеграл запишется так:
2
222
11
,.
111
U
R dU
UUU
+++
∫
Пример 1. Вычислить интеграл
32
44
sin sin
sin .
cos cos
xx
dx xdx
xx
=
∫∫
Пусть
cos ,Ux=
тогда
sindU xdx= −
и последний интеграл примет вид
2
4 24 3 3
11 1 1
( 1) .
cos
3 3cos
1
CC
Ux
Ux
U dU dU
dU
U UU
− = − =−+ +=− + +
−
∫ ∫∫
Пример 2. Вычислить интеграл
2
4
.
sin
cos
x
dx
x
∫
Положим
tg ,Ux=
тогда
arctg ,xU=
21
)
(1
d
dx U U
−
= +
и
2 2 22
4 22
(1 )
(1 ) (1 )
sin
cos
U dU
UU
xU
dx
x
+
⋅=
++
=
∫∫
23 3
/3 (1/3)tg .dU U C x C
U
= = += +
∫
§ 11. Интегрирование иррациональных функций
с помощью тригонометрических замен
Рассмотрим интеграл Здесь подинтегральная
функция – рациональная функция своих аргументов, – заданные дей-
ствительные числа,
0a ≠
. Преобразуем подкоренное выражение. Вынесем за
скобки а затем полученное выражение дополним до полного квадрата
суммы:
( )
2
2
/(2 ) /(4 ).ax b a c b a= + +−
Введём обозначения
( )
sin cos .R x xdx
∫
sin ,Ux=
( )
sin cos
x
dU x dx xdx
′
= =
( )
.R U dU
∫
( )
cos sin .R x xdx
∫
cos ,Ux=
sin x
cos x
tg ,xU=
arctg ,xU=
2
,
1
dU
dx
U
=
+
2
2
1
cos ,
1 tg
x
x
=
+
2 22
sin tg cos .x xx=
22 2
sin /(1 ).
xU U
= +
(
)
2
2
,.J R x ax bx c dx= ++
∫
R
,,abc
,a
2
ax bx c+ +=
2
,am= ±
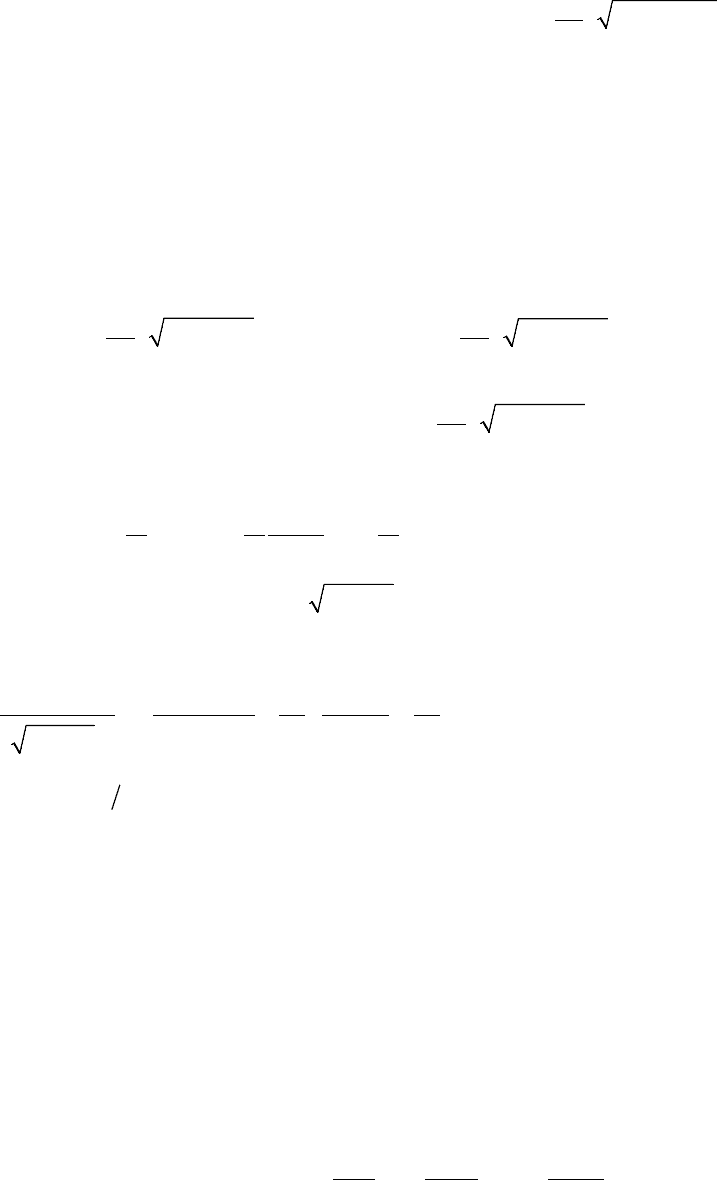
207
22
/(4 ) .
cb a n−=±
Здесь знаки правых частей мы должны считать совпадающи-
ми со знаком левой части в каждом выражении, например, если
0,a >
то бе-
рём если то Кроме того, в рассматриваемом интеграле
сделаем замену Отсюда
/(2 ),xtb a= −
значит, Теперь
исходный интеграл принимает вид Здесь, пере-
брав знаки перед слагаемыми под корнем, получим четыре различных случая,
так как каждый из знаков первого слагаемого сочетается с каждым из знаков
второго слагаемого. Однако один из случаев, когда под знаком корня стоит
, мы должны отбросить, так как получаем отрицательное подкорен-
ное выражение и, соответственно, мнимую величину. Таким образом, остаёт-
ся рассмотреть лишь три следующих варианта:
22 2
2
,;
2
b
J R t m t n dt
a
=−+
∫
Чтобы избавиться от корня, необходимо сделать следующие замены соответ-
ственно:
Пример. Вычислить
Сделаем замену при этом отсюда
(
)
3
33 2 2 2
22
cos 1 1
.
cos cos
dx n UdU dU
tgU C
n U n Un
nx
= = = +
−
∫∫ ∫
Здесь согласно замене
Замечание. В дальнейшем мы докажем, что для любой непрерывной
функции
()fx
существует первообразная
()Fx
, т. е. неопределенный интеграл
()()dx F x Cfx = +
∫
(см. §4 главы 12). Но, оказывается, не всегда этот неопределенный интеграл
представляет собой элементарную функцию, т. е. не всегда он может быть
представлен одной формулой, выраженной через конечное число основных
элементарных функций. К таким интегралам относятся
2
sin cos
,, ,
ln
x
dx x x
dx dx dx
xx x
e
−
∫ ∫∫ ∫
и т. д.
2
,am= +
0,a <
2
.am= −
/(2 ) .xb a t+=
.
t
dx x dt dt
′
= =
22 2
2
,.
2
b
J R t m t n dt
a
= − ±±
∫
22 2
mt n−−
22 2
2
,;
2
b
J R t m t n dt
a
=−−
∫
2 22
2
,.
2
b
J R t n m t dt
a
=−−
∫
tg ;
n
tU
m
=
1
;
cos
n
t
mU
=
sin .
n
tU
m
=
(
)
3
22
.n x dx
−
−
∫
sin ,xn U=
cos ,
U
dx x dU n UdU
′
= =
arcsin( ).U xn=

5354.ru
208
ГЛАВА 12. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. Площадь криволинейной трапеции
Пусть на плоскости задана кривая
уравнением где и
– соответственно абсциссы точек и
Будем считать, что в указанном интервале
всюду Это значит, что кривая
лежит выше оси (приведённые далее
рассуждения справедливы и для случая, ко-
гда ).
Рассмотрим фигуру, ограниченную свер-
ху кривой и снизу отрезком оси а с боков – отрезками
aA
и
,bB
параллельными оси
Oy
(см. рис. 109) Эту фигуру назовем криволинейной
трапецией и её площадь обозначим
.
aABb
S
Будем искать площадь криволинейной трапеции. Разобьём интервал
на частей точками так, что каждая следующая точка лежит пра-
вее предыдущей, пусть при этом Здесь мы получим интерва-
лов, которые будем называть частичными интервалами:
Длины каждого из этих интервалов обозначим
В указанных интервалах возьмём соот-
ветственно произвольные точки (которые могут совпадать также с
концами интервалов). Найдём – ординаты точек кривой
с абсциссами На первом, втором, …, -м частичных ин-
тервалах, как на основаниях, построим прямоугольники, высоты которых
равны соответственно
( ) ( ) ( )
1
, 2, , .
n
ff f
ξξ ξ
Площадь полученной фигуры, со-
ставленной из этих прямоугольников, обозначим . Она будет равна сум-
ме площадей прямоугольников, из которых эта фигура составлена:
(1)
Коротко сумму (1) будем записывать с помощью символа суммирования
следующим образом:
Oxy
AB
( )
,,y fx a x b= ≤≤
a
b
A
.B
( )
0.fx>
AB
Ox
( )
0fx≥
AB
[ ]
,ab
,Ox
[ ]
,ab
n
12 1
, ,...,
n
xx x
−
0
,.
n
axbx= =
n
[ ]
01
,,xx
[ ] [ ]
12 1
, , ..., , .
nn
xx x x
−
110 2 21
; ;...xxx x xx∆= − ∆= −
1
.
nnn
xxx
−
∆= −
12
, ,...,
n
ξξ ξ
( ) ( ) ( )
12
, ,...,
n
ff f
ξξ ξ
( )
y fx=
12
, ,..., .
n
ξξ ξ
n
n
n
S
( ) ( ) ( )
11 22
... .
n nn
S f xf x f x
ξξ ξ
= ∆+ ∆+ + ∆
∑
Рис. 109
209
(2)
Чтобы вместо (2) иметь (1), нужно вместо индекса поочередно подставить
значения и полученные произведения сложить. Ясно, что площадь
зависит от способа разбиения интервала
[ ]
,,ab
так как точки разбиения
влияют на длины оснований прямоугольников. Кроме того, пло-
щадь зависит от выбора точек
12
, , ... , ,
n
ξξ ξ
так как их выбор влияет на высоты прямоугольников.
Пусть есть наибольшая из длин частичных интервалов, на которые мы
разбили интервал
[ , ].ab
Число делений устремим к бесконечности так, что-
бы стремился к нулю. При этом все частичные интервалы стягиваются
в точки, а ступенчатая фигура с площадью приближается по форме к кри-
волинейной трапеции. Таким образом, естественно за площадь криволиней-
ной трапеции
aABb
S
принять величину
1
max 0
lim ( ) .
i
n
aABb i i
n
i
x
S fx
ξ
→∞
=
∆→
= ∆
∑
(3)
При этом будем считать, что предел правой части не зависит ни от способа
разбиения
[,]ab
на частичные интервалы, ни от выбора точек
§ 2. Определение и геометрический смысл
определённого интеграла
Пусть в интервале задана функция которая, в отличие
от предыдущей (§1), может принимать в этом интервале как положительные,
так и отрицательные и нулевые значения. Интервал разобьём на ча-
стей точками Каждая последующая точка лежит
правее предыдущей. Длины частичных интервалов соответственно равны
2 21 1
;...; .
nnn
xxx xxx
−
∆= − ∆= −
Внутри первого, второго, … , -го ча-
стичных интервалов возьмём произвольные точки (они могут сов-
пасть и с концами самих интервалов). В этих точках вычислим значения за-
данной функции и образуем сумму
( )
1
.
n
n ii
i
S fx
ξ
=
= ∆
∑
i
1, 2,..., n
n
S
12 1
, ,...,
n
xx x
−
n
S
( )
i
f
ξ
max
i
x∆
n
max
i
x∆
n
S
12
, ,..., .
n
ξξ ξ
[ ]
,ab
( )
ab<
( )
,fx
[ ]
,ab
n
0 12 1
, , ,..., , .
nn
x ax x x x b
−
= =
n
110
;xxx∆= −
n
12
, ,...,
n
ξξ ξ
( )
fx
5354.ru
210
( ) ( ) ( ) ( )
11 22
1
... ,
n
n nn ii
i
S f xf x f x f x
ξξ ξ ξ
=
= ∆+ ∆+ + ∆ = ∆
∑
(4)
которая называется интегральной суммой для функции на интервале
где функция задана.
Если при и
max 0
i
x∆→
интегральная сумма (4) имеет конечный
предел, не зависящий ни от способа разбиения интервала на частичные
интервалы, ни от выбора точек , то этот предел называют опреде-
лённым интегралом от функции по интервалу и обозначают
Итак, по определению
( ) ( )
1
max 0
lim .
i
b
n
ii
n
i
a
x
f x dx f x
ξ
→∞
=
∆→
= ∆
∑
∫
(5)
В этом случае говорят, что функция интегрируема в интервале
Числа называют соответственно нижним и верхним пределами интеграла,
– подинтегральной функцией, – дифференциалом переменной –
переменной интегрирования, – интервалом интегрирования.
Теорема 1. Если функция непрерывна в то она в этом интер-
вале интегрируема.
Иначе говоря, для этой функции существует конечный предел интеграль-
ной суммы, составленной для неё по интервалу Этот предел не зависит
ни от способа разбиения ни от выбора точек
Теорема принимается без доказательства.
Геометрический смысл определенного интеграла заключается в следую-
щем. Если всюду в то правая часть формулы (5), согласно (3),
равна площади криволинейной трапеции, следовательно,
() .
b
aABb
a
f x dx S=
∫
Эта
трапеция ограничена снизу интервалом сверху – кривой с уравне-
нием где – подинтегральная функция, с боков – отрезками и
В правую часть формулы (5) не входит переменная интегрирования Это
означает, что определённый интеграл представляет собой число и не зависит
от обозначения переменной интегрирования. Буква может быть любой,
например, или , при этом
( )
fx
[ ]
,,ab
n →∞
[ ]
,ab
12
, ,...,
n
ξξ ξ
( )
fx
[ ]
,ab
( )
.
b
a
f x dx
∫
( )
fx
[ ]
,.ab
,ab
( )
fx
dx
,x
x
[ ]
,ab
( )
fx
[ ]
,,ab
[ ]
,.ab
[ ]
,,ab
12
, ,..., .
n
ξξ ξ
( )
0fx≥
[ ]
,,ab
[ ]
,,ab
AB
( )
,y fx=
( )
fx
aA
.bB
.x
x
t
