Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. т а ін. Вища математика у прикладах та задачах. Ч 3
Подождите немного. Документ загружается.


§3.
Диференціювання функцій комплексної змінної
331
д
2
и д
2
—-
+ —- = 2а + 2с = 2(а + с) = 0 => а = -с.
дх
2
ду
2
При а = - с заданий тричлен є гармонічною функцією. ^
Приклад 13. Задана пара гармонічних функцій и(х, у) і
у(х,у).
Довести, що ці функції спряжені.
и(х,
у) = е
х
со§
у
+
\, V(x, у) =
1
+ е
х
зіп у .
•
Перевіримо виконання умов Коші-Рімана.
ди
дх
ди
—
=е соз
у,
дх
ду , ди ду
—
= е соз у =>
——
= перша умова виконується.
ду дх ду
ду
х • ду
х
. ди
—
= -е зіп у, — = е зіп у => — =
ду дх ду дх
Отже, задані гармонічні функції спряжені. ^
-
друга умова виконується.
Приклад 14. Довести, що добуток спряжених гармоніч-
них функцій и(х,у) і
V(x,у)
в області И буде гармонічною
функцією в цій області.
•
Оскільки функції гармонічні, то вони задовольняють рівняння Лап-
ласа, тобто
д
2
у д
2
у д
2
и д
2
и
п
„ . „ . .
—7 + —7 = 0, —- + —- = 0.
дх' ду~ дх ду
Нехай
МІ
= и(х,у)
•
у(х,у) . Треба довести, що
д
2
м> д
2
м>
дх
2
ду
2
= 0.
д\у ди ду д~м> д и „ ди ду д V
—
= — -У+
—
-И, —- =—--у +
2——
+
—-и;
дх дх дх дх' дх' дх дх дх
Зи> ди ду д
2
м> д
2
и _ ди ду д
2
У
——
= —--У +
——
и, —— =
—г-'У
+ 2——н ~"и.
ду ду ду ду ду ду ду ду
Тоді
м> д
2
м>
Ґі2
дх
1
ду
1
2..
\
у
+ 2
V
/а2
д
1
у д
1
у
[дх
2+
ду
2
)
и = Аи-у + 2
д
1
и д
1
и
—Г + —7
дх
2
ду
2
{
ди ду ^диду^
дх дх ду ду
( ди ду ди ду
+
|+
дх дх ду ду
+АУ•и.

332
Глава 3. Функції комплексної змінної
Оскільки и(х, у) і у(х,у) спряжені гармонічні функції, вони задоволь-
няють рівняння Лапласа, тобто А и = 0, АУ = 0, і задовольняють умови Коші-
ди ЗУ ди ЗУ ,
Рімана — = —, — , тобто
Зх Зу Зу Зх
ди ЗУ ди Зу ди ди ди ди
+ = + - = 0.
Зх Зх ду ду дх ду ду дх
Отже,
Ам>
= Аи
•
V + 2
ди ЗУ ди ЗУ ^
-
+ ——— + Ду-и = 0.
^
Зх Зх ду ду )
Таким чином, функція >у = и(х, у)-у(х,у) задовольняє рівняння Лап-
ласа, тобто є гармонічною. А
Приклад 15. Знайти коефіцієнт розтягу і кут повороту при
відображенні
МІ
= 2
2
в точці г
0
• Знайдемо похідну
и/=.(2
2
)'
= 2
2
.
Тоді
м>] ^
+(
^ = 2(л/2+/л/2) = 2л/2+/2л/2 .
Перейдемо до тригонометричної форми запису комплексного числа і
одержимо
Звідси
'42 .41
—+/—
2 2
= 4
л . л
С05
—
+ г 51П
—
4 4
"II
а
= 4 , аг§ и'І,
тобто коефіцієнт розтягу г = 4 , а кут повороту ш = — . А
4
IV. Задачі для практичних занять
3.72.
Знайти всі точки, в яких диференційовні задані функції.
а)
\\>
= Ке і; б)
м>
=
|
г \
2
; в)
м>
= г Ке 2;
г)
м>
= Іт г + і
К.е
2.
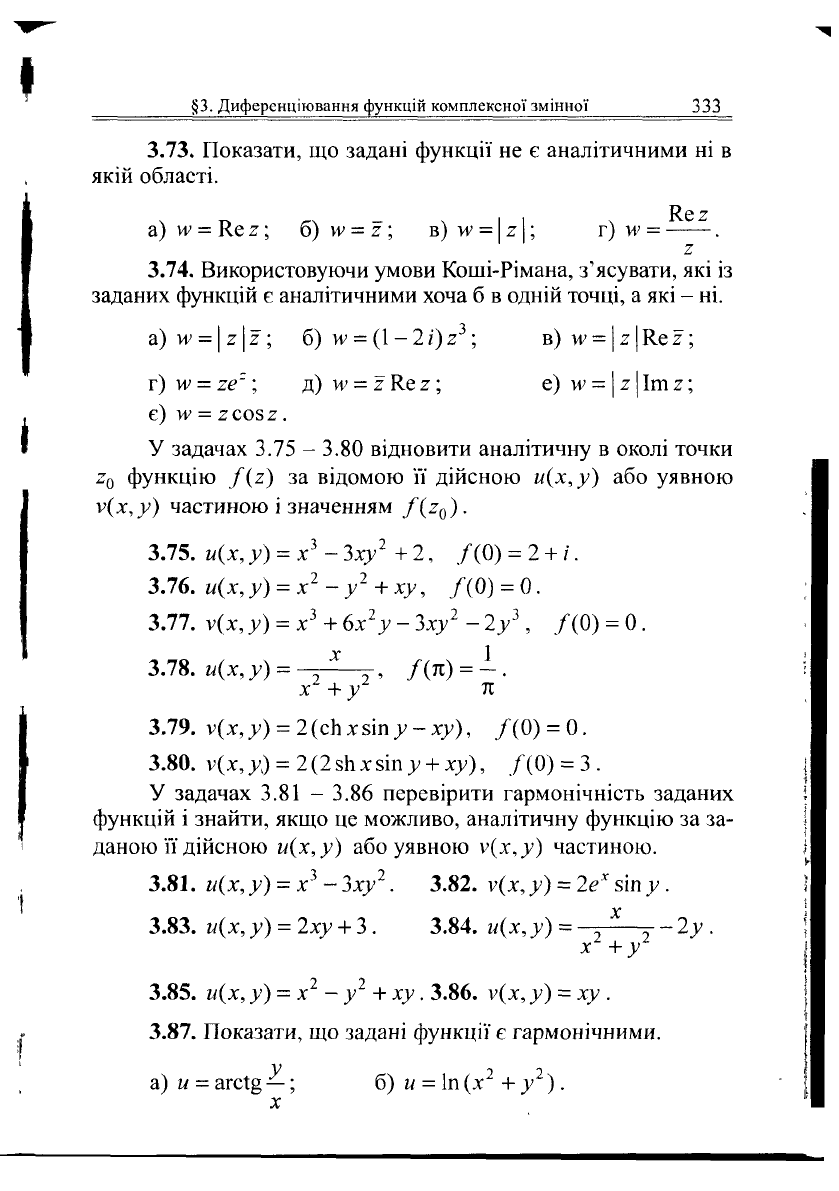
§3.
Диференціювання функцій комплексної змінної
333
3.73.
Показати, що задані функції не є аналітичними ні в
якій області.
а)
XV
= Ке г ; б)
XV
= ї; в)
мг
=
І
21;
г)
м>
=
2
3.74.
Використовуючи умови Коші-Рімана, з'ясувати, які із
заданих функцій є аналітичними хоча б в одній точці, а які - ні.
а)
м>
=
|
г
|
г ; б)
м>
=
(1
- 2 і) 2
і
; в)
м>
=
121
Ке г ;
г)
и>
= 2е~; д) н- = 2 Ке 2; е)
м>
=
121
Ігл 2;
Є)
IV = 2
СОЗ
2 .
У задачах 3.75 - 3.80 відновити аналітичну в околі точки
2
0
функцію /(г) за відомою її дійсною м(х, у) або уявною
у) частиною і значенням
/(2
0
).
3.75.
^) = х
3
- Зх>>
2
+ 2, /(0) = 2 + /.
3.76. и(х,у) =
х
2
-у
2
+ху, /(0) = 0.
3.77. у(х,^) = х
3
+ 6х
2
зу - Зх^
2
- 2у
г
, /(0) = 0 .
х 1
3.78. и(х, у) = — у, /(я) =
—
.
х +у П
3.79.
у(х, у) = 2 (сЬ х зіп у - ху), /(0) = 0.
3.80.
у(х, у) = 2 (2 зп х зіп у + ху), /(0) = 3 .
У задачах 3.81 - 3.86 перевірити гармонічність заданих
функцій і знайти, якщо це можливо, аналітичну функцію за за-
даною її дійсною ^(х,^) або уявною
V(x,^')
частиною.
3.81.
и(х, у) = X
і
- Зх_у
2
. 3.82.
у(х,у)
= 2е
х
зіп у .
X
3.83.
и(х, у) = 2ху + 3 . 3.84. и(х, у) = —г т- - 2у .
х
1
+ у
1
2
2
3.85.
и{х,у) = х -у + ху. 3.86. у(х,у) = ху .
3.87. Показати, що задані функції є гармонічними.
у 2 2
а) и = агсі§ —; б) и =
1п
(х + у ).

334
Глава 3, Функції комплексної змінної
3.88. Задано пари гармонічних функцій и(х, у) і
У(Х,
у).
Знайти серед них спряжені пари гармонічних функцій.
а) и(х, у) =
3
(х
2
- у
2
), у(х, у) = Зх
2
у - у
3
;
X V
6)и(х,у) = — -,
у(х,у)
= =
х+у х+у
в) и(х,у) = х,
у(х,у)
= -у.
3.89. Знайти коефіцієнт розтягу г і кут повороту ф при
заданих відображеннях
м>
= /(г) в заданих точках.
а)
XV
= е у точках 2
Х
= Іп 2 + /
—
і 2
2
=-\-г
—
\
б)
IV
= зіп 2 у точках 2, = 0 і 2
2
=
1
+ /;
в)
УУ
—
2 у точках 2, = 2 - / 1 2
2
=
1
+ / —.
§4.
Інтегрування функцій комплексної змінної
І. Короткі теоретичні відомості
Основні поняття і формули для обчислення інтегралів. Нехай зада-
на деяка орієнтовна крива С , в кожній точці якої задана функція комплекс-
ної змінної и> = /(г). Розіб'ємо криву С на п довільних частин точками
2
0
,2[,...,2
Л
.
У кожній частині візьмемо довільну точку \
к
, знайдемо
та сформуємо інтегральну суму
І/(*и)Дг*,
к=\
ДЄ
Д2
А
= 2*
-2
к
_\.
Позначимо X = шах | Аг
к
|
.
я
Означення. Якщо існує границя Ііт У./(^ )Аг
к
, яка не залежить
від способу розбиття кривої С та вибору точок Ь,
к
, то ця границя назива-
ється інтегралом від функції
м>
= /(і) вздовж кривої С та позначається
1/(2)02.
С

§4.
Інтегрування функцій комплексної змінної
335
Отже,
за
означенням
//(2)
й
к=1ітХ/(^)Аг*.
(3-30)
Нехай
2 =
х
+
іу, /(г)
=
и
+ іг,
де
и =
и(х,у),
у =
г(х,у)
-
дійсні функції змінних
х та у .
Обчислення інтеграла
від
функції комплексної змінної
2
зводиться
до обчислення криволінійних інтегралів другого роду:
|У(2)сіг
= ^(и
+ іу)(ах +
іау) =
|исіх
-
Vсіу +
і^и
сіу +
V
сіх
.
(3.31)
г
с с г
На інтеграли від функцій комплексної змінної розповсюджуються всі
властивості криволінійних інтегралів другого роду.
Інтеграл ^ /(г) сі:, взагалі кажучи, залежить від шляху інтегрування
С .
с
Якщо
/(2) -
аналітична функція
в
однозв'язній області
й , то
інтег-
рал
не
залежить від форми шляху інтегрування.
В
цьому випадку
1/(2)сІ2
= 0,
(3.32)
де
Ь -
будь-який замкнений кусково-гладкий контур
в
області
£>
(див. далі
основну теорему Коші).
Якщо крива
С
задана параметричними рівняннями
х =
х(і), у
=
у(і)
або задана
в
комплексній формі
2(1)
= х(()
+
іу((),
і початкова
та
кінцева точки дуги
С
відповідають значенням параметра
/
= а, / =
(3,
то
Р
\Г(2)СІ2
=
\ГШ}2\
{
)СІІ.
(3.33)
Г
а
Тут 2(1)
=
Х
(()
+іу(1).
Якщо функція
/(г)
аналітична
в
однозв'язній області
О , яка
міс-
тить точки
2
0
та
2|,
то
має місце формула Ньютона-Лейбніца
]/(2)сІ2
=
Ф(2)\1
=ф(
г
,)-ф(2
0
),
(3.34)
де Ф(г)
-
будь-яка первісна для функції
/(2),
тобто Ф'(г)
=
/(2)
в
області
О.

336
Глава 3. Функції комплексної змінної
Якщо функції
/(2) і ф(г)
аналітичні
в
однозв'язній області
О ,а 2
0
та
2]
-довільніточки цієї області,
то
має місце формула інтегрування частинами
|Л2)-ф'(2)^2 = [Л2)ф(2)]|^ -'1ф)/Ь)сЬ
.
(3.35)
-0
-о
Заміна змінної
в
інтегралах
від
функцій комплексної змінної викону-
ється аналогічно випадку функції дійсної змінної.
Нехай аналітична функція
2 =
ф(и") взаємно однозначно відображає
контур
С) в
площині
IV на
контур
С в
площині
7. .
Тоді
має
місце формула
заміни змінної
\/(г)02
= ІЖ»МХ*)А».
(3.36)
с
с,
Якщо шляхом інтегрування
є
півпряма (промінь),
що
виходить
з
точ-
ки
2
0
або
коло
з
центром
у
точці
2 = 2
0
, то
корисно робити заміну змінної
вигляду
2-2
0
=геТ
(3.37)
У першому випадку
ф =
сопзг,
а г -
дійсна змінна інтегрування,
у
другому випадку
г =
соші,
а ф
—
дійсна змінна інтегрування
Якщо
2
0
= 0 , то
отримуємо заміну змінної вигляду
2
= ге"
9
.
(3.38)
Інтегральна формула Коші
Якщо функція
/(2) є
аналітичною
в
області
О ,
обмеженій кусково-
гладким замкненим контуром
С , і на
самому контурі,
то
справедлива інтег-
ральна формула Коші
Я2,)
= ^-Л^-сЬ,
(3.39)
2л і
}. г-г
0
де
2
0
є
£>, контур
С
обходиться так,
що
область
О
залишається весь
час
зліва.
Інтегральна формула Коші дозволяє обчислювати деякі інтеграли,
при
цьому формула (3.39) використовується
у
вигляді
\4^І02
= 2л
і
Дг
0
).
(3.40)
с
2
- Ч
Якщо функція
/(2)
аналітична
в
області
О і на її
межі
С , то для
V
л є N має
місце формула
для
похідної
п -го
порядку

§4.
Інтегрування функцій комплексної змінної
337
№
СІ7.
,
(3-41)
2гс//.(
2
-_-
0
)»
+І
де :
0
єО, гє С .
Формула (3.41)- формула для похідної п -го порядку аналітичної функ-
ції. Ця формула дозволяє обчислювати деякі інтеграли, при цьому вона ви-
користовується у вигляді
А*)
;
У
(п)
(ч)
Г(2-
20
Г
+І
ах = 2тс/
п\
(3.42)
Теорема Коші
Теорема І (основна теорема Коші). Якщо функція у (і) аналітична
в однозв'язній області В , обмеженій контуром Сі/-- замкнений контур
в й, то
І.
Якщо функція /(і) неперервна в замкненій області 0 = £) + С,то
\/(г)еЬ = 0. (3.43)
с
Теорема 2 (узагальнена теорема Коші). Якщо функція /(г) аналітич-
на в многозв'язній області О, обмеженій контуром С і внутрішніми по
відношенню до нього контурами у
і
,
у
2
,...,
, і неперервна в замкненій
області О = О + С
+
+ у І" + У2 +... + у^, де знаки верхніх індексів означають
напрямки обходів, то
\У(ї)аг = 0. (3.44)
; = 1
Теорема 2 є теоремою Коші для многозв'язної області. На рис.3.12
наведена многозв'язна область з обмежуючим її контуром. Вказано напрям-
ки обходу межі.
С
Рис.3.12

338
Глава
3.
Функції комплексної змінної
З формули (3.44) маємо
\/(2)(Ь=І/(2)сЬ+
1/(2)02
+ ...+
1/(2)02.
(3.45)
(' її Ї2 1к
Формула (3.45) використовується
для
обчислення деяких інтегралів.
//.
Контрольні питання та завдання
1.
Дайте означення інтеграла від функції комплексної змін-
ної вздовж кривої
С.
2.
Наведіть формулу, що зводить обчислення інтеграла
від
функції комплексної змінної
до
обчислення криволінійних
ін-
тегралів другого роду
від
функцій дійсних змінних.
3.
Наведіть формулу для обчислення інтеграла від функції
комплексної змінної вздовж кривої
С для
випадку, коли крива
С задана параметричними рівняннями.
4.
Запишіть формулу Ньютона-Лейбніца
для
обчислення
інтеграла
від
функції комплексної змінної.
За
яких умов вона
має місце?
5.
Запишіть формулу інтегрування частинами. За яких умов
вона
має
місце?
6. Наведіть формулу заміни змінної.
Яка
заміна викорис-
товується
для
випадку, коли шляхом інтегрування
є
коло
з
центром
у
ТОЧЦІ
2 = 2
0
; у
ТОЧЦІ
2 = 0?
7.
Запишіть інтегральну формулу Коші.
Як
вона викорис-
товується для обчислення інтегралів?
8.
Запишіть формулу для похідної
п
-го порядку аналітич-
ної функції.
За
яких умов вона
має
місце?
Як
вона пов'язана
з
інтегральною формулою Коші?
9. Сформулюйте основну теорему Коші.
10.
Сформулюйте узагальнену теорему Коші.
11.
Як
використовується узагальнена теорема Коші для
об-
числення інтегралів?

§4.
Інтегрування функцій комплексної змінної
339
///.
Приклади розв'язання задач
Приклад 1. Обчислити інтеграл ^(\ +
і-2г)сІ2,
де С -
с
лінія,
що з'єднує точки 2, = 0 і 2
2
=
1
+ і (рис.3.13), якщо:
а) С - пряма;
б) С - парабола у = х
2
;
в) С - ламана
2
х
г
г
г
г
,
де 2
3
= 1.
•
Перепишемо підінтегральну функцію у вигляді
/(г) =
1
+ /-2г = (1-2х) + /(1 + 2у) .
Тут и =
1
- 2х, у =
1
+ 2_у .
Застосувавши формулу
| /(г)сІ2
= ^исіх -
V
сіу + і |у сіх + и сіу,
с с с
маємо
|(1 +
і-2І)сІ2
=
\(\-2х)сіх-(\
+ 2у)сіу + і\(\+2у)сіх + (\-2х)сіу .
с с с
Рис.3.13
а) С - пряма.
Рівнянням прямої, що проходить через точки 2| = 0 і г
2
=
1
+ /, буде
у = х , а звідси сіу = сіх, 0 < х < 1, тому
|(1+
/-22)02
= |(1-2х)ох-(1 + 2у)ф; + /|(1 + 2>')А: + (1-2х)й^ =
с є
-
с
1
1 11
= /((]- 2х) -
(1
+ 2х))Л + /|((1 + 2х) +
(1
- 2х))Л = -[4х
сіх
+ /\2
сіх
=
0
0 0 0
= -2 + 2/ = 2(/-1).

340
Глава 3. Функції комплексної змінної
б) С - парабола у = х .
Для параболи у = х
2
маємо ау -Іхсіх, 0 < х < 1. Звідси
\'\
+
і-2г)аг
= |(1 - 2х)сіх - (1 + 2у)ау + і |(1 + 2у)сіх + (\ - 2х)ау =
С
С V
і 1
4
= |(1 - 2х -
(1
+ 2х
2
)2х)ЙХ
+ і|(1 + 2х
2
+ (1 - 2х)2х)ах = -2 +
т
і .
оо
в) С - ламана
г
і
2
3
і
2
,
де 2
3
= 1 .
На відрізку 2,2
3
: у = 0, ау = 0, 0 < х <
1
; на відрізку
2
3
2
2
:
х = І,
сіх = 0, 0 < у < 1 . Використовуючи властивість лінійності криволінійного
інтеграла, матимемо
|(1 + /-22)йЬ= ](1 +
(-22)02+
_[(1 + ї-22)£& =
= |(1-2х)<£с-(1 + 2у)с/у + і |(1+2у)с& + (1-2х)с/у +
-1-3
г
1
;
3
+ _[(І-2х)<&-(1+2у)с/у +
г
|(1 + 2у)с6с + (1-2х)й(у =
:
3-2
г
3
:
2
І
II І
= \{\-2х)ах + і\ах-\0+2у)ау + і\<\-2\)сіу = -2.<
0
0 0 о
Приклад 2. Обчислити інтеграл / =
12
Іт 2
2
сіг,
де С: |г| =
1
(-тс<аг§2<0)
(рис.3.14).
•
Застосуємо формулу
| /{г)сІг
=^исіх-усіу + і^уахл-иау,
с
с с
ДЄ
/(2) = М + /У, 2 = Х + /у.
Тоді 2
2
=х
2
- у
2
+2ху/,
ІШ2
2
=2ху .
У
і
1
1
Рис.3.14
