Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. т а ін. Вища математика у прикладах та задачах. Ч 3
Подождите немного. Документ загружается.

§4,
Інтегрування функцій комплексної змінної
34]
У нашому випадку /(2)
=
2Іт2
,тому
/(і)
=
гітг
2
=
2х
2
у + і2ху
2
,
де и
= 2х
2
у,
\
= 2ху
2
.
Тоді
/
=
^г\хпт.
2
ах
=
|2х
2
у ах
—
2ху
2
ау +
і
_|2ху
2
ах + 2х
2
у
ау =
с
о
= 2
|(С05
2
ф(-8ІП
2
ф)-5ІП
2
фС05
2
ф)сЛр +
Х
=
С05ф,
Л =
-8ІПф<Лр
У
=
5ІПф,
йу =
С03ф<Лр,
-л<ф<0
+ 2І
|((-ЗІП
3
ф)с03ф
+
ЗІПфС05
3
ф)<Лр = 21
1
?
'
—
зіп
2ф
2
СІЦ>
+
.
о
+
2/1
— зіп2фсоз2ф
сіц>
= —
|(1 -соз4ф)і/ф +
—
|зіп4ф<Лр
=
1
(
зіп4ф
2
Г 4~
і
(
соз4ф
Приклад
3.
Обчислити інтеграл
|
(г
2
+
22)
сіг, де
С -
дуга
с
кола
121
=
1
(0 <
аг§2
< тс) (рис.3.15).
•
Для обчислення інтеграла скористаємось формулою
\№<ь
=
|/мої
•*'(')<*.
Нехай
2 =
/-е
,(р
.
При /•
=
1 маємо
2 =
е
,<р
. Тоді
|(2
2
+
22)йЬ
=
2
= Є
СІ2=Іе"*СІЧ?
0<ф<я
= |(У
2<р
+1)/У
ф
<Лр
=
= /|(е'
3ір
+
е'
ф
)#
= [д
е'
3(
Р+
е
"Р
І'

342
Глава 3. Функції комплексної змінної
-•О 1
х
Рис.3.15 -4
і
Приклад 4. Обчислити інтеграл
|гсоз2аг.
о
•
Для обчислення інтеграла скористуємось формулою інтегрування
частинами
|
/(г)ф'(г)аЬ =
[/(г)ф)]\1
-
]ф(2)/'(г)аЬ.
-о
-о
У нашому випадку функції /(г) = 2 і ф(г) = соз 2 - аналітичні всю-
ди.
Застосовуючи формулу інтегрування частинами, одержимо
ІгсозгоЬ =
|2(зіп2)'о2
= (гзіпг) ^ -|зіпгсіг = /зіп/ + созг\'
0
=
1
= /зіп і + соз / -1 = -зЬ
1
+ сп
1
-1 =
е'-е-
1
е
1
+е'
]
•
1.<
Приклад 5. Обчислити інтеграл ^Хпгсіг (Іпг - головне
с
значення логарифма), де С : | г1 = 1, за умови, що
а) початок шляху інтегрування 2
0
=
1
(рис.З.Іба);
б) початок шляху інтегрування г
0
= -1 (рис.3.166).
Обхід проти годинникової стрілки.
•
Для обчислення інтеграла скористаємось формулою
Р
С
а
а) початок шляху інтегрування 2
0
=
1
.
Покладемо г = ге"
9
. При г = 1 маємо г = е"
9
. Отже,
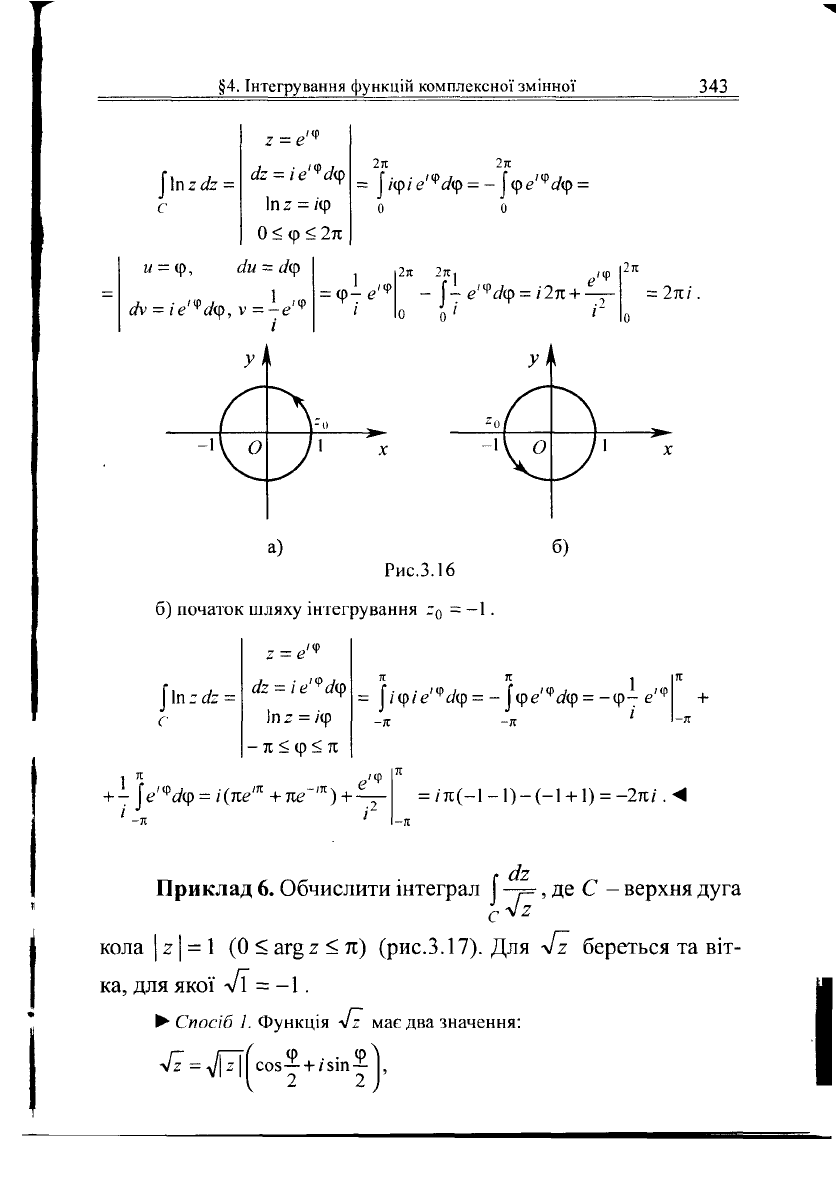
§4.
Інтегрування функцій комплексної змінної
343
^\\\2СІ2
••
2
=
Є
'
Ф
сІ2
= іе"*сІу
ІП
2 = /ф
0 < ф < 2л
и = ф, сій =
сі<р
2 тс
2тс
= |/ф/'е'
Ф
^ф = -|фе'
Ф
^ф:
Л = /е'
ф
а'ф,
У=І
Є
'
Ф
= ф- Є
І
2тс
2тг,
0
о
_|-е'
ф
я'ф = /2л + -^
2тс
:
2Л/ .
У )
л
>
}
*
а)
Рис.3.16
б) початок шляху інтегрування 2
0
= -1.
2
= е'
Ф
сіг = /й'
ф
а'ф
б)
| ІП
2
СІ2
=
ІП
2 = /ф
• 71
< ф < П
= }/ф/е'
ф
б/ф = -|фе'
ф
і
/ф = -фіе"
р
+
- ]Є^СІЦ> = і(ТСе
т
+
7СЄ~
Т
)
+ £-
'
2. і
:/Л(-1-1)-(-1
+ 1) = -2Л/.^
сіг
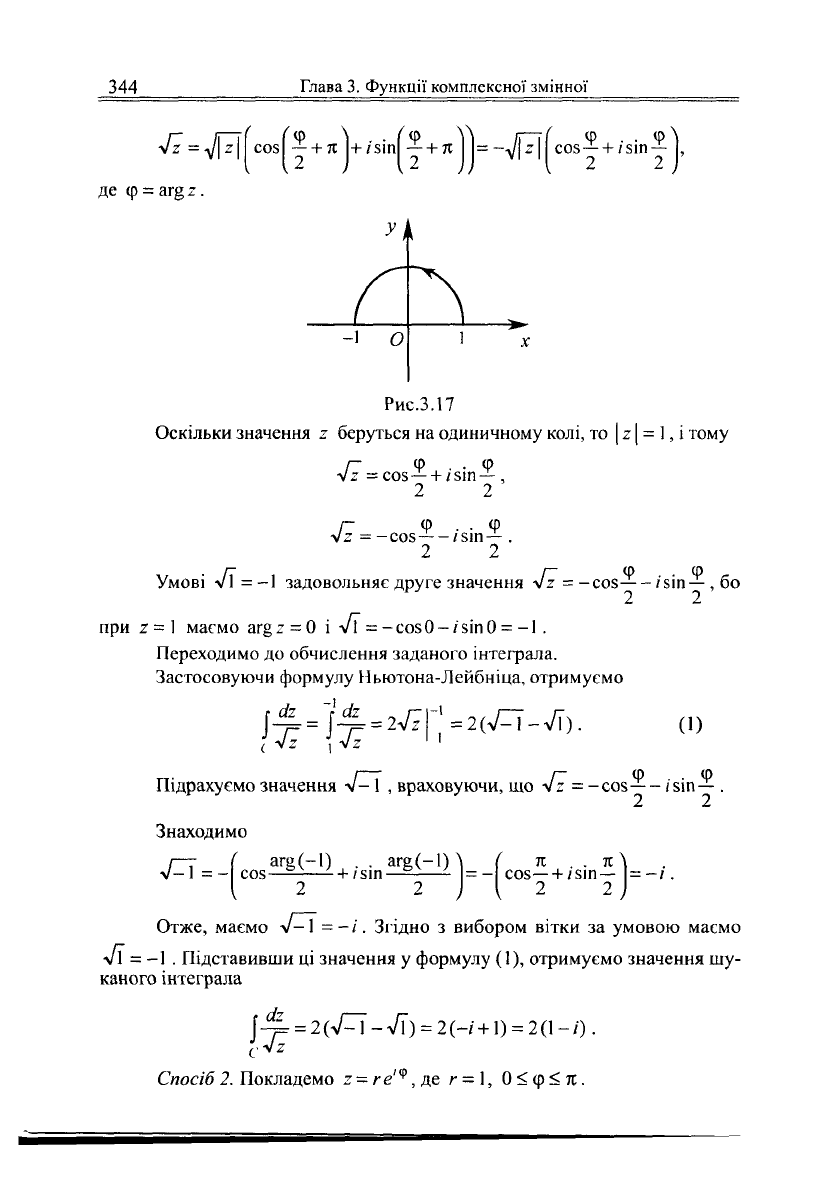
Приклад
6. Обчислити інтеграл
\—==,
де С - верхня дуга
С
\2
кола
|
21
=
1
(0 <
аг§
г <
ж)
(рис.3.17). Для 4г береться та віт-
ка,
для якої
VI
=
-1.
•
Спосіб І. Функція л/7 має два значення:
'
ф . ф^
СОЗ — + /5ГП —
344
Глава 3. Функції комплексної змінної
77 =
де ф = аг§г.
СОЗ
— + Л \+1
12
ЗІП
ф
+
Я =-л/ 2
ф
. . ф
СОЗ — + /51П —
2 2
ґ
-і
о
1 X
Рис.3.17
Оскільки значення 2 беруться на одиничному колі, то
121
= 1, і тому
Г Ф • • Ф
•Я2 - СОЗ—+ /51П — ,
2 2
Г Ф • • Ф
УІ2 = -СОЗ (ЗІП— .
2 2
Умові л/Т = -1 задовольняє друге значення л/7 =
-созу-
/зіпу , бо
при 2 =
1
маємо
аг§2
= 0 і л/Т = - созО - / зіп 0 = -1 .
Переходимо до обчислення заданого інтеграла.
Застосовуючи формулу Ньютона-Лейбніца, отримуємо
1-12
, л/2
11
(1)
Підрахуємо значення -1-Х , враховуючи, що
>/7
= -соз-^- /зіп-^ .
аге(-І)
. . аге(-1)А ( п . . тс ,
СОЗ——
-+(31П—— =- СОЗ—+ /ЗІП — =-/.
2 2 [ 2 2
Знаходимо
Отже,
маємо л/-Т = - /. Згідно з вибором вітки за умовою маємо
VI = -1 . Підставивши ці значення у формулу (1), отримуємо значення шу-
каного інтеграла
|-^
= 2(лП-7Г) = 2(-/ +
1)
= 2(1-/).
С
ЛІ2
Спосіб 2. Покладемо 2 = ге"
9
, де г = 1, 0 < ф < тс.

§4.
Інтегрування функцій комплексної змінної
345
З умови
VI =-1
випливає,
що ^г'' =е'
2
'.
Дійсно, перевіримо
цей факт, поклавши
ф = 0.
Маємо л/е'
ф
=
л/Т
=
е'*
0+7С
^
=
-1.
Переходимо
до
обчислення заданого інтеграла.
•
2е
ск
2
= е
,<р
= іе"*сіц
0<ф<гс
0
(
-і
71
\
--2
е
2
-е~
0
\
)
о
ме
•
2(~і + \) =
2(\-і).<
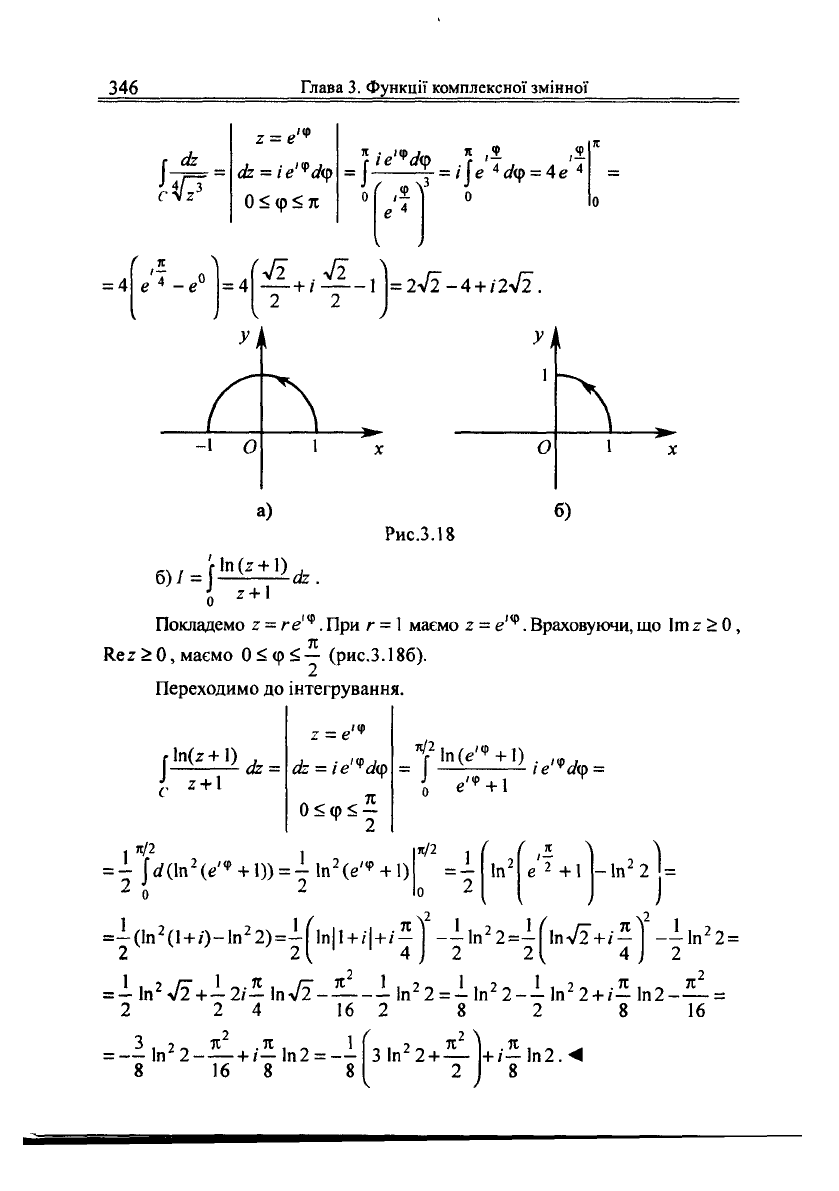
Приклад
7.
Обчислити задані інтеграли:
г
СІЇ І,
а)
/ =
І
—==,
де С -
верхня половина кола
|
2 \ —
1
с
У2
3
(0
<
аг§г
<
тс) (рис.3.18а),
за
умови,
що
вибирається
та
вітка
функції
XV
= V?, для
якої л/Т
= 1;
б) / -
Г
Ш
(
2 +
^ (І
г
ВЗДОВЖ ДуГИ КОЛа
І2І = 1,
ІГП2>0,
о
^
т 1
Ке2>0
(рис.3.186).
• .)/ =
/*
Покладемо
г = ге . При г
—
1 маємо
2 = е
ф
,
тоді
VI
=
ІІе~^=е~~*~,
* = 0,
1,2,3.
(1)
Виберемо таке значення кореня,
щоб
задовольнити умову
Мї = 1.
Маємо
0+2кж
1/ї
=
№ = е
4
=1 при к = 0.
д
Поклавши
к = 0 у
формулі
(1),
отримуємо
Переходимо
до
інтегрування.
346
Глава
3,
Функції комплексної змінної
•47
ск
=
іе
ІЧ,
сі<р
0<ф<л
= Г
Ц-
= і\е
4
<Лр
= 4е
І —
4
о
=
4
І
1
е'*-е
й
=
4
П
(
4Ї
.4Ї ,
—+
, 1
2
2
V
=
2л/2-4
+
/272
.
-1
О
1
О
б)/=|
а)
г 1п
+
б)
Рис.3.18
2+1
Покладемо
2 = ге
ф
.
При
г =
1
маємо
г = е
ф
.
Враховуючи,
що
Іт 2 > 0,
Кег
> 0,
маємо
0 < ф <
— (рис.3.186).
Переходимо
до
інтегрування.
•ІП(2
+ 1)
.
2 +
1
2
=
0<ф<-
т
2
:
\
———-ІЄ
Ф
</ф =
тс/2
=
-
|<з(1п
2
(е'
ф
+ 1)) =
-1п
2
(У
,|
'
+ 1)
о
л/2
]
(
X \
1 —
л/2
]
1п
2
е
2
+1
о
=
2
1
1п
2
2^
=
-І1п
2
2
:
2
=
І1„2
72
+
І
2/
1
,
Пл
/2"-^-І1п
2
2=І1п
2
2-ііп
2
2
+ /^
1п2-^І
=
2
24 16 2 8 2 8 16
->
2 і / 2
4
3,2^ТС
.ТС , „ 1 '
= —1п
2
2
+ /— 1п2 = —
8
16 8 8
=-(1п
2
(1
+
/)-1п
2
2)Л('іп|1
+ /| + /^|-І1п
2
2=-[іп72+/-
>
2
2 ^
4)2 2\ 4
;
З
1^2 + —
|+/-Іп2.««
2
8

§4,
Інтегрування функцій комплексної змінної
347
Приклад 8. Користуючись інтегральною формулою Коші,
обчислити інтеграл \~ <іг, якщо:
с г - 6г
а) С
:
| г -
21
= 1; б)С:|г-2| = 3; в)С:|г-2| = 5.
• а) С:|г-2| = 1.
У замкненій області, обмеженій колом | г - 21 =
1
(рис.3.19а), підінтег-
ральна функція аналітична, тому в силу теореми Коші
2
|г-2|
=
1
Г
~
6Г
б) С: |г-2| = 3.
Всередині області, обмеженої колом | 2 - 21 = 3 (рис.3.196), знаходить-
ся одна точка г = 0, в якій знаменник підінтегральної функції перетворю-
ється в нуль. Перепишемо інтеграл у вигляді
.2
Є"
|;:-2|
= 3
2
~
6г
\г-2\
=
3
2
(
2 6
) |г-2|=3
2-6
аг.
Функція /(х) =
2-6
тегральну формулу Коші у вигляді
аналітична в даній області. Застосовуючи ін-
2-2п
аг = 2пі/(г
0
), 2
0
= 0,

348
Глава 3. Функції комплексної змінної
в) С: \2-2\ = 5.
В області, обмеженій колом |г-2( = 5 (рис.3.19в), знаходяться дві
точки 2 = 0 і 2 = 6, в яких знаменник підінтегральної функції перетворюєть-
ся в нуль. Безпосередньо формулу Коші використовувати не можна. В цьо-
му випадку для обчислення інтеграла можна зробити так.
Спосіб 1. Розкладемо дріб —-^— на суму найпростіших дробів.
Маємо
1
2-62
1
2
1_
_
6
2
2~-б2
6 2-6
Підставляючи в інтеграл, одержимо
1_
]_
6
2
і
7
1^-2
|=*
2
Ог= —
[ ——аг-— [ ——
"6г
6
|;
_2|=5
2_6
б
|-'-2|
= 5
2
1
02 =
=— 2кіе
:
6
1
—
2кіе~
2=6
6
=
—
те'
=о
З
,36
1 . е
36
-1 .
•— ПІ
= КІ .
З З
Спосіб 2. Побудуємо два кола "/) і у
2
3
центрами в точках г = 0 і
2
= 6 достатньо малих радіусів, таких, щоб кола не перетнулись і цілком
містились в крузі
12
-
21
< 5 , як зображено на рис.3.19в). В тризв'язній об-
ласті,
обмеженій колами | г - 21 = 5 , у, і у
2
, підінтегральна функція всюди
аналітична. За теоремою Коші для многозв'язної області
12-21=5
г
2
-6г
-62
Ї2
2
2
-62
•аг.
До кожного інтеграла можна застосувати інтегральну формулу Коші.
Тоді одержимо
І--2
1=5'
2
•62
02= |
= 2л/-
2-6
-2л/-
2=0
.-2|=5
2(2-6)
сіг= \^^аг+ Г
:
2
^
02
Чг
е
іь
-\
кі, А
2=6
Приклад
9. Обчислити задані інтеграли:

§4.
Інтегрування функцій комплексної змінної
349
К2
1)/=
|
=2
81П-
2
і
+22-3
сіг;
6)1
=
І
І&2
ііг:
-
=і
8ІП2
8ІГі(г-1)
2Є
:+2
1=2
2
і
-2
іІ2 .
•
При обчисленні користуватимемось інтегральною формулою Коші.
Кожний приклад супроводжується рисунком, де відзначаються точки, що
належать області £), обмеженої контуром С,вяхихзнамеігникпідінтеграль-
ної функції перетворюється в нуль.
.
7Г2
8ІП-
2
а)
7 = [ — =—
й2
.
{:
_І
н
г
2
+2г-3
В точці 2=1 знаменник обертається в нуль
(рис.
3.20а).
81П- 81П-
ТС2
|.-1|=2
.
пг
51П
2_
,
и,- \ ?— [ -^±1
2
2
+2г-3 ..X,
(2+3)(2-1)
2-1
сіг =
І--4=2
сіг =
І--4=2
81П
2 2хг/ я/
а)
1 х -2\ о
б)
Рис.3.20
б)/= |
І§2
В)
У точці 2 = 0 знаменник обертається в нуль (рис.3.206).

350
Глава
3.
Функції комплексної змінної
/=
|
-Щ-аг=
\ ск =
2кі/{0)
=
2піЩ0І
2
=0.
-і
~2
1
2Є
г+2
и
=1
.
. г
8ІП23Іп(2-1)
,
в)
/ = ^ —^— ^ •
|ф2
2
"
2
Перетворимо
(•
ЗІГ)23Іп(2-1)
, (•
8ІП25ІП(2-1)
,
/=
г аг = аг.
1*1=2
2
~
г
14-2
2(2 _1)
У точках
2 = 0 і 2 =
1 знаменник обертається
в
нуль (рис.3.20в).
Побудуємо
два
кола
Ті і Уг
3
центрами
в
точках
2 = 0 і 2 =
1
і
раді-
усів
<
—
(щоб
вони
не
перетинались
і
цілком містились
в
крузі
| г 15 2). За
теоремою Коші
для
многозв'язної області
5ІП2-8ІП(2-1)
ЗІП28Іп(2-1)
є
ЗІП23ІП(2-1)^
=
Г:
*-1
й2+
Г-
2
ІФ2
'('"І)
І
2
і -1
Далі
за
інтегральною теоремою Коші
,
~ . г • /•
,,ч
^ .
зіпО-віп(О-І)
. .
зіпі-8Іп(1-1)
.
/
=
2л//, (0)
+
2л/
•
/
2
(1)
= 2я/ ^ + 2л/ р = 0,
,
. .
8ІП2-8ІП(2-1)
. . .
8ІП2-8ІП(2-1)
.
Де/і(г)
= ; ~,
/
2
(
г
)
= " --^
Приклад
10.
Обчислити інтеграл
[ ііг.
,4=2(2
+
1)
3
(2-1)
•
Спосіб
1.
Знаменник
(г +
3)
3
(2-1)
підінтегральної функції пере-
творюється
в
нуль
в
точках
г = -1 і 2 = 1, що
містяться всередині круга
121
< 2 .
Розкладемо підінтегральну функцію
на
суму найпростіших дробів.
1 111111
11
(2
+
1)
3
(2-1)
8 2-1 8 2 +
1
4 (
2
+ 1)
2
2 (
2
+ 1)
3
Використовуючи лінійність інтеграла, отримуємо
[
с
*1 \ ^Ог-± \ ^-аг-
,4
=2
(2
+
1)
3
(2-1)
«ІФ2
2
-
1
8
|ф2
2
+ 1
