Тевяшев А.Д., Литвин О.Г. Вища математика. Загальний курс: Збірник задач та вправ
Подождите немного. Документ загружается.


2.23.
125.
127. •
л'і + 3*2
_
*з = 3 ;
2л*[ + х
2
+ 2х
3
=
5 'у
Х| - Х2 + Зхз =
3
;
Зх] + 4х
2
- 7х
3
= 0 .
х\
- 5x2
+
3*з
_
х
4
= 1 ;
2х[ - 10х
2
+ Зх
4
= 0 ;
4х| - 20х
2
+ 6x3 + х
4
= 2 .
Х| + Х2 - Зх
4
- 4x5 =
О
А'і
+ х
2
- х
3
+ 2х
4
- Х5 = 1 ;
2Х[ +2x2
+
*3
-
*4
+
3*5 = 0
2.24.
2.26. {
X] + 2x2 + Х3
—
— 1 ;
2х) + Зх
2
+ 5х
3
= 3 ;
Зх) + 5x2
+
6*3
= 7
.
2х] + 3x2 ~ *3 + *4
=
2
х\
+ 2x2
+
*3 ~ х
4
=
1
Зх, + 5х
2
= З
X] + х
2
- 2хз + 2х
4
=
1
У задачах 2.28 - 2.30 розв'язати однорідні системи рівнянь . Викорис-
~зти метод Гаусса (або метод повного виключення):
2.28.
130.
2.29.
х\
+ 2х
2
- Зх
3
+ х
4
= 0 ;
2хі + 4x2
_
х
3
- х
4
= 0 ;
Зхі + 6x2 - 4х
3
= 0 .
(2хі + х
2
- х
3
= 0 ;
[ Х[ - х
2
+ х
3
= 0 .
2х| +3x2 ~4хз
=
0
Х|
—
2х
2
+3х'з = 0
Зх] + х
2
- х
3
= 0
5х] + 4х
2
-5х
3
= 0 .
У задачах 2.31 - 2.32 знайти фундаментальну систему розв'язків :
2*1 + *2
_
4х
3
= 0 ;
131.
Х[ + х
2
+ Зх
3
- 2х
4
+ Х5 = 0 ;
І
Зх( + 2х
2
+ Зх
3
- х
4
+ 2x5 = 0 .
2.32.
і
Зхі + 4х
2
- Х3 = 0 ;
X] + Зх
2
+ ЗХ3 = 0 .
У задачах 2.33-2.37 знайти власні вектори і власні значення матриці А:
133.
А =
135.
А =
1 -1
2 4
' 1 1
0 1
1 1
2.34. А =
V
4
-2^
-З
о
1
2.36. А
=
2^
4
-2
2.37. А =
•1 2^
—
^
0
61

4.
7.
10.
13.
2.4. Індивідуальне завдання 2
Задача 1.Обчислити визначник четвертого порядку.
Варіанти завдань
114 0
0-3 2 1
2 1-12
-13 0 4
2.
2 3 0
-2 0 4
5 6 1
3 5 2
4 0
З -1
1 2
2 4
1 2
2 0
-1 1
-З З
-1 2 0
3 2
0 4
0
1 -1
1 -
-1
1 -3
1
2
5.
2
1 8
3
2 0 3 1
2 -4
2
0
-4
3
-9 1
-1 1 0
2
3 -5 1
-
8 6
1 10
3
3 2 1 --1
3 1 -
-3
4
-1 2
->
:)
0 1 -1
2
1 1 --1
2
1
_
3
-2 1
. 9.
3 -4 7
8.
. 9.
-1 2 2 0 2
-
3 -5 2
-1 2
3
0 3 1 2
3
1
-7 3
2
-3
5
3 0
1 0
1 2
3
4
-1
3
1
-3 1
-1 3
11.
2
5
8
9
12.
1 2 -1
-3 1
-1
11.
12.
1 -1
6 2
1 5
3 8 0 2
2 1 -3
9 4 2 1
4 3 3 3
3
-7 -5
5 4 3 2
4 3 2 І
0 1 2
3
4 2 2 1
14.
3 4 0 7
15.
1
2
0 - 4
14.
15.
1 0 -
3 2 3 4 2 4 6 8
2 1 3 -
-1
2 4 5 3
1
1
2 3
-3 3 1
0
4
•6
5
4
12
15
62

2
1 -1
3
3 1 2
3
1
2
.)
4
.6.
. 4
2
0
-2
1
3
1
0
.
17.
6
-3
4
2
-1
" 0
0
5
.
18.
-1
1
0 -
3
1
1
2
-1
-2
3
1 -1
3 -1 2 1 2 1
6
0
2 0 1 -
-1
1
-1
0 4
3
1
0
1
9.
0
1
1
-1
2
0
2
1
.
20.
-1
2
2
-1
3
1
0
1
.
21.
2
3
1
-1
-1
2
1
2
-1
2 3 4
1
3
0 --1 -2 0 -1
1
3 1
-7
0
1 -1
2
3
4 1 --1
2 1
22.
-1
1
2
-І
0
-у
4
2
.
23.
0
_ 1
2
1
3
0
1
4
.
24.
0
2
3
І
1
1
1 1
о!
і
0 4 -2 1
2 3 -2 1
2
-1
0 3 |
. 1 1 -1 3 3 1 2 -1 -1
2
0
->
0
25.
-1
2
2
1
3
0
1
4
.
26.
2
1
1
2
0
1
-1
0
.
27.
1
1
_2
2
1
2
-3
0
-1
-1
1 -4
-2 -3 1
2
-1 3 0 4
2
3
-1
2
-3 1 0 5 2
3
4
5
28.
4
4
7
0
1
1
4
3
.
29.
3
6
-2
-3
1
2
-4
1
.
30.
1
2
3
7
2
5 4
-2 -4
2
3
6
2
1
0
-10
2
11
2-315
0 5 14
1-10
2
4-131
63
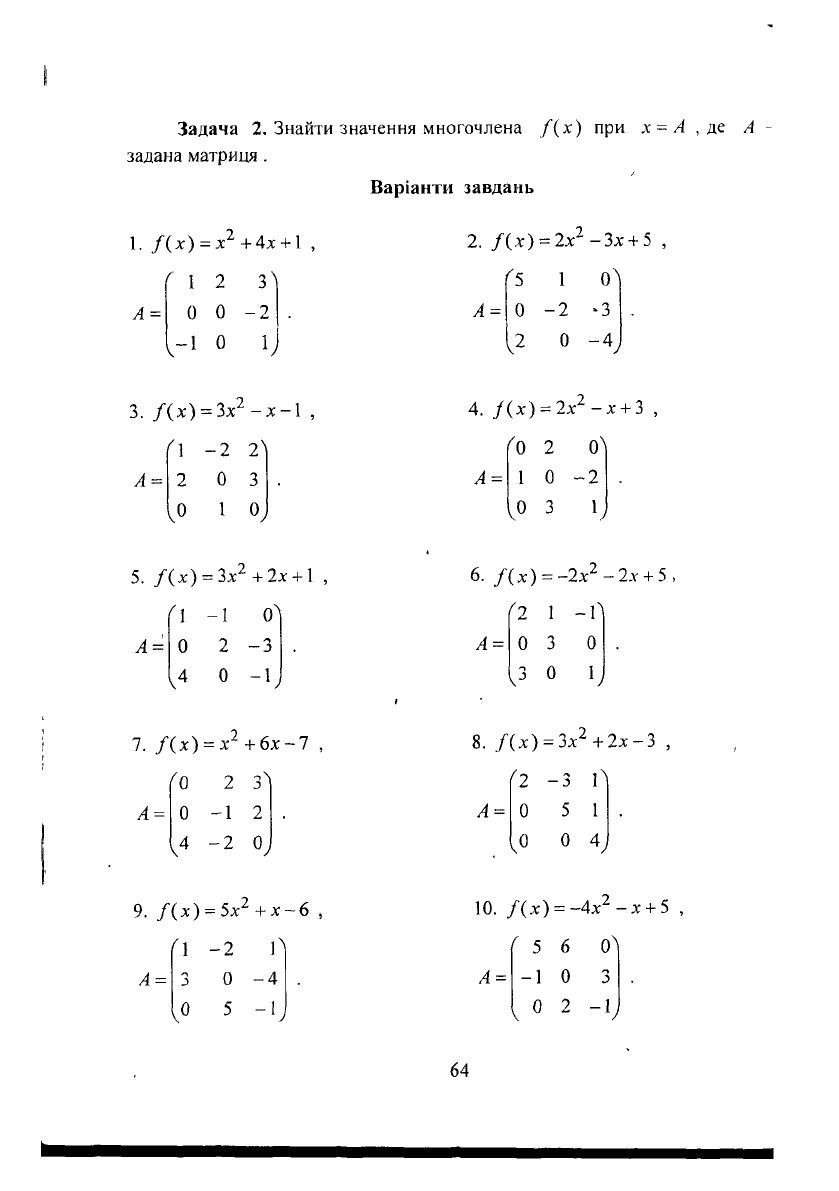
Задача 2. Знайти значення многочлена /(х) при х = А , де А
задана матриця .
Варіанти завдань
1.
/(х) = х^+4х +
1
,
М 2 3^
А= 0 0-2
•1 0 1
3.
Дх) = 3х
/
-х-1 ,
'1 -2 2\
А= 2 0 3
ч
0 1 0,
4.
/(х) = 2х^ - х + 3
'О 2 0^
А= 1 0 -2
1°
3
ь
5.
/(х) = 3х
/
+2х +
1
,
'\ -1 0^
Л= 0 2-3
,4 0 -1,
v
6. /'(х) = -2х
2
-2х + 5:
А =
2 1 -П
0 3 0
3 0 1,
7.
Дх) = х
г
+6х-7 ,
^0 2 3^
/1
=
0-12
4-2 0
. Дх) = 3х
г
+2х-3 ,
ґ
2 -З П
А= 0 5 1
0 0 4;
9. Дх) = 5х
2
+х-6 ,
О -2 1
Л
А= 3 0-4
,0 5 -1
V
10.
Дх) = -4х -х + 5 ,
( 5 6 0^
Л= -1 0 З
ч
0 2 -1
у
64
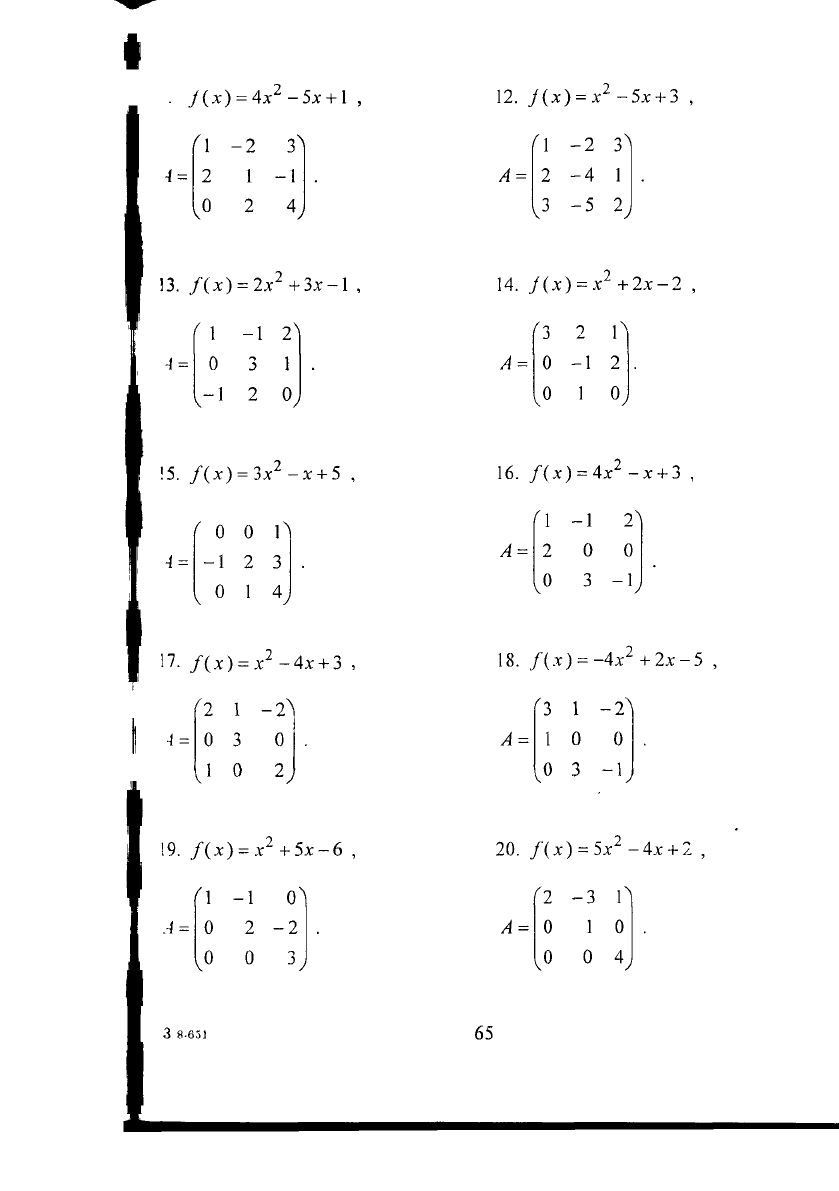
і(х)
=
Ах
1
-5х +
1
12.
Дх) = х -5х + 3
ґ
\ -2 З
л
2 1 -1
0 2 4
V
1 -2 З
2 -4 1
3-5 2
13.
Дх) = 2х
2
+3х-1
1 -1 2Ї
0 3 1
-12 0
14.
Дх) = х^ +2х-2
(З 2 \\
0-12
0 1 0
!5.
Дх) = 3х
2
-х + 5
16.
Дх) = 4х
/
- х + 3
(
0 0 1
л
12 3
0 1 4
у
А =
1 -1 2
2 0 0
0 3-1
17.
Дх) = х
2
-4х +
3
,
(
2 1 -2^
1 =
V
0 3 0
1 0 2
18.
Д.г) = -4х
/
+2х
А =
З 1 -2
1 0 0
0 3-1
19.
Дх) = х
2
+5х-6 ,
20.
Дх) = 5х -4х +
.4
=
'і -1 0
Л
0 2-2
0 0 з
у
А =
ґ
2 -3 1
л
0 1 0
0 0 4
у
З 8-631
65
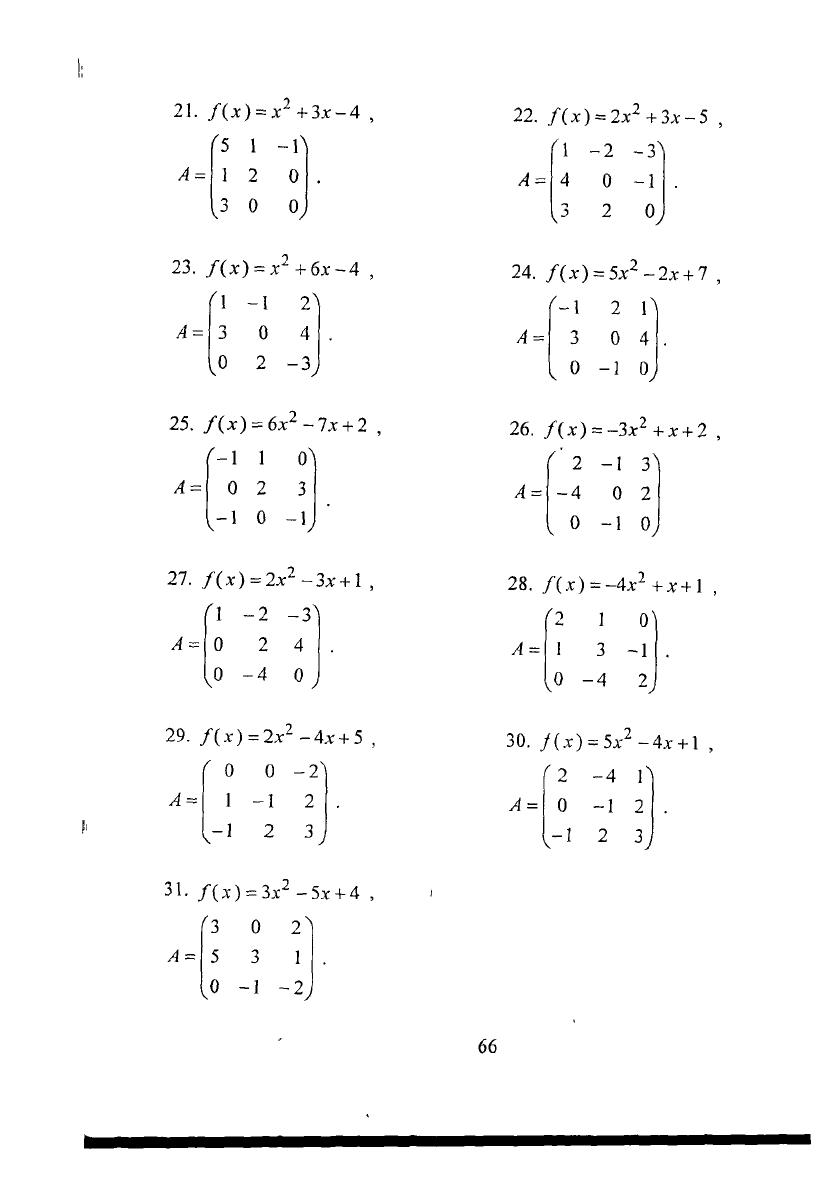
21.
/(х) = х
2
+Зх-4 ,
ґ
5 1 -Г\
1 2 О
,3 О О,
23.
/(х) = д:
2
+6д:-4 ,
'1 -1 2^
3 0 4
,0 2 -З,
25.
Дх)==6х
2
-7х + 2 ,
'-1 1 0>
0 2 3
,-1 0 -1,
27.
Дх) = 2х
2
-3х +
1
,
'1 -2 -3^
Л= 0 2 4
ч
0 -4 0;
22.
Дх) = 2х
2
+Зх-5
ґ
\ -2 -3^
4 0-1
А =
0
24.
Дх) = 5х
2
-2х + 7
'-1 2 Л
А= 3 0 4
, 0 -1 о
у
26.
/(х) = -3*
2
+х + 2
2 -1 3^
-4 0 2
^ 0 -1 0
у
28.
Дх) = -4х
2
+х+1
'2 1 0Ї
А = 1 3-1
29.
Дх)=2х
/
-4х + 5 ,
г
0 0 -2"і
1 -1 2
х
-1 2 3;
31.
Дх) = Зх
2
-5х + 4 ,
'З 0 2
Л
А= 5 З 1
,0 -1 -2,
30.
Дх) = 5х
2
-4х +
1
Ґ2 -4 О
Л = 0 -12
-12 3;
66
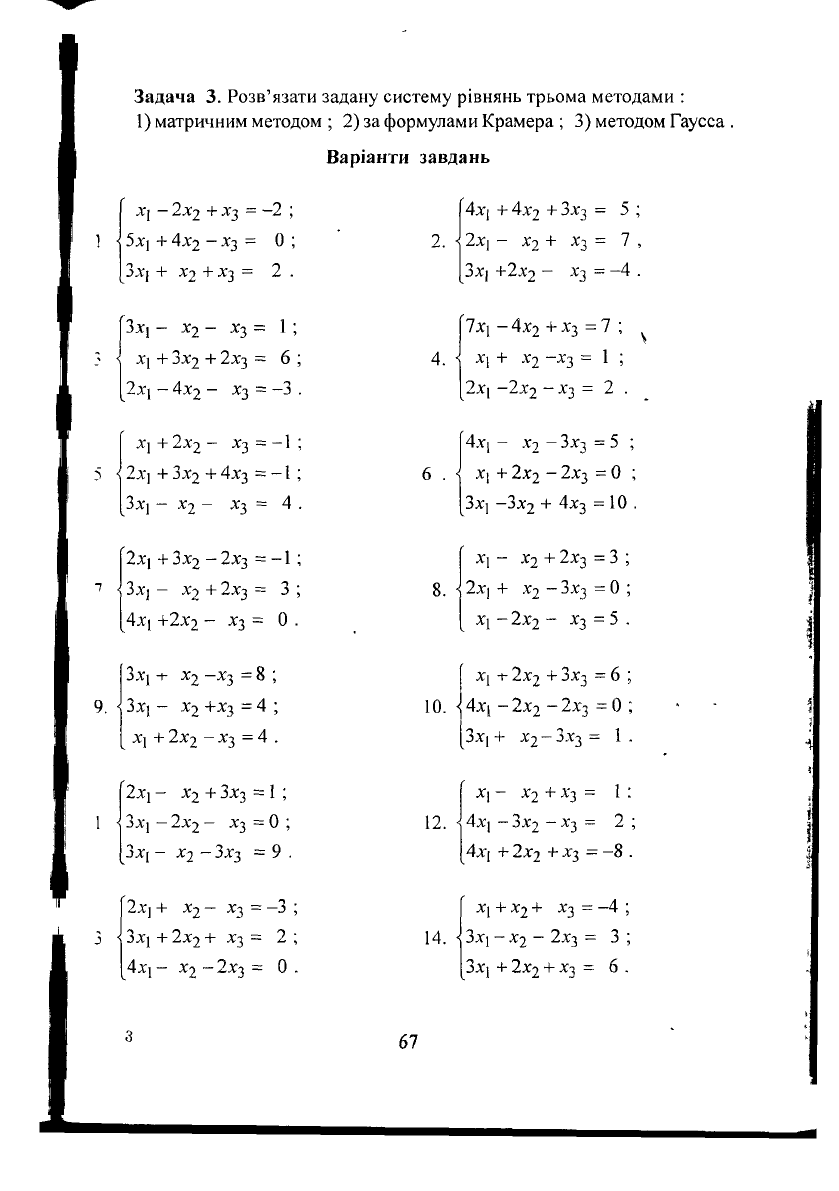
Задача 3. Розв'язати задану систему рівнянь трьома методами :
1) матричним методом ; 2) за формулами Крамера ; 3) методом Гаусса
Варіанти завдань
X,
-
2х
2
+
*з
=
~2 ;
5х\
+
4x2
~ *3
=
0
Зх, + х
2
+ хз = 2 .
Зх,
-
*2- *3=
1
1
*1
+
3X2
+
2*3
=
6
ІХ\
- 4x2
_
Хз = -3
X]
+
2x2
_
х
3
= -1
<
2х, + Зх
2
+ 4х
3
= -1
Зх,
-
*2 " *3 =
4
2х|
+
3x2
~~
2х
3
= -1
-
Зх,
-
х
2
+ 2х
3
= 3
4х,
+2x2
- х
3
= 0
Зх,
-і-
х
2
-х
3
= 8 ;
•
Зх,
-
х
2
+х
3
= 4 ;
1
*1
+
2х
2
- х
3
= 4 .
2х,
-
х
2
+ Зх
3
=
1
;
13*і
-
2х
2
- хз = 0 ;
Зх,
-
х
2
- Зхз = 9 .
2х,
+ х
2
- хз = -3
13*і
+
2х
2
+ хз = 2
4х,
-
х
2~
2хз
= 0
4х,
+ 4х
2
+ Зх
3
= 5 ;
2.
•!
2х,
- х
2
+ х
3
= 7 ,
Зх,
+2х
2
- х
3
= -4 .
7х,
- 4х
2
+ х'з = 7 ;
4.
•! х, + х
2
-хз = 1 ;
2х, —2х
2
—
Х3
= 2 .
4х,
- х
2
- Зх
3
= 5 ;
6 . { х, + 2х
2
-
2x3
= 0 ;
Зх, -Зх
2
+ 4х
3
= 10 .
х, - х
2
+ 2х
3
= 3 ;
2х,
+ х
2
- Зх
3
= 0 ;
х,
—
2x2
~ *3
=
^ •
х,
-і-
2x2
+
3*з = 6 ;
10. \4х
{
-2х
2
-2х
3
=0 ;
Зх, +
х
2
-3х
3
= 1 .
12.
<
14.
х, - х
2
+ х
3
= 1 :
4х, - Зх
2
- х
3
= 2 ;
4х, + 2х
2
+ х
3
= -8 .
х, + х
2
+ х
3
= -4 ;
Зх, - х
2
- 2х
3
= 3 ;
Зх, + 2х
2
+ х
3
= 6 .
З
67
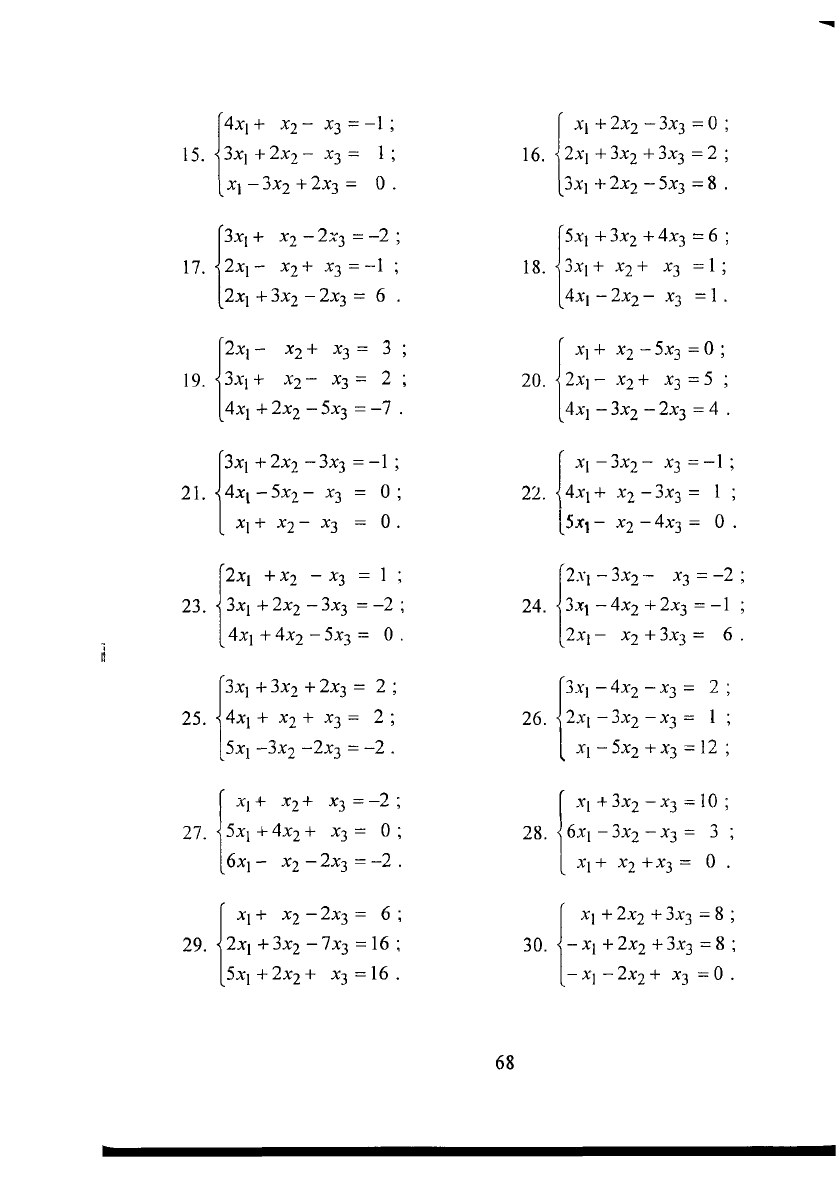
15.
17.
{
19.
4х,
+ х
2
- х
3
= -1 ;
Зх] +
2х
2
- х
3
= 1 ;
X] -
Зх
2
+
2х
3
= 0 .
Зх] + х
2
-
2х
3
= -2 ;
2х,
-
х
2
+
х
3
= -1 ;
2х,
+
Зх
2
-
2х
3
= 6 .
2х|
- х
2
+ х
3
= 3 ;
Зх,
+ х
2
- х
3
= 2 ;
4х[ +
2х
2
-
5х
3
= -7 .
16.
21.
{
23.
25.
Зх,
+
2х
2
-
Зх
3
=
4х,
-
5х
2
- х
3
=
х, + х
2
- х
3
=
2х[ + х
2
- х
3
Зхі +
2х
2
-
Зх
3
-
4х,
+
4х
2
-
5х
3
-і;
0;
о.
27.
29.
<
Зх,
+
Зх
2
+
2х
3
= 2 ;
4хі + х
2
+ х
3
= 2 ;
5хі
-Зх
2
-2х
3
= -2 .
X) + х
2
+ х
3
= -2 ;
5х,
+
4х
2
+ х
3
= 0 ;
6х,
- х
2
-
2х
3
= -2 .
х, + х
2
-
2х
3
= 6 ;
2х,
+3х
2
-7х
3
= 16 ;
5х] +
2х
2
+ х
3
= 16 .
20.
<
22.
24.
26.
28.
<
ЗО.
і
х
\
+
2х
2
-
Зх
3
= 0 ;
2х\
+
Зх
2
+
Зх
3
=
2;
Зх,
+
2х
2
-
5х
3
= 8 .
'5х,
+
Зх
2
+
4х
3
= 6 ;
•Зх,
+ х
2
+ х
3
=
і;
4х,
—
2х
2
—
х
3
= 1 .
X,
+ х
2
-
5х
3
= 0 ;
-
х
2
+
х
3
= 5 ;
4х, Зх
2
2х
3
= 4 .
X,
-Зх
2
-
х
3
=
-і;
•
4х,
+ х
2
-
Зх
3
= і ;
[5х,
- х
2
-4х
3
= 0
2л-,
-Зх
2
-
х
3
= -2
•
Зх,
-
4х
2
+
2х
3
= -1
2х,
- х
2
+
Зх
3
= 6
'Зх,
-
4х
2
- х
3
= = 2 ;
•
2х,
-Зх
2
-х
3
=
= 1 ;
X,
-
5х
2
+ х
3
=
= 12 ;
X,
+
Зх
2
- х
3
=
= 10 ;
< 6х
"
3
*2 -
х
3
=
= 3 ;
X
+ х
2
+х
3
= 0 .
х, +
2х
2
+
Зх
3
= 8 ;
- х, +
2х
2
+
Зх
3
= 8
- х, -
2х
2
+ х
3
= 0 .
68

Х\+
х
2
+ Хз = 6 ;
2х] + х
2
+ Зх
3
=13;
Х\ + 2х
2
+ Зхз = 14 .
Задача 4. Дослідити сумісність системи , і у випадку сумісності знай-
ти загальний розв'язок та один частинний розв'язок системи . Виконати пе-
ревірку правильності частинного розв'язку .
Варіанти завдань
X] + 2хз
—
Х4 = 0 ;
Зх] + х
2
+ 6x3 - ЗХ4 = 3 ;
4х] - х
2
+ 8x3 - 4x4
= -
3 ;
2х] + х
2
+ 4хз - 2х
4
= 3 .
2. \
Зх[ - 2х
2
+ Х3 = -1
2Х] + х
2
- Х3 - 4х
4
= -4
Зх, - х
2
+ 2х
3
= 1
Х[ + 2х
2
+ х
3
- 2х
4
= 1
Х| + х
2
- ЗХ3 = -1
Х| - Зх
2
- ЗХ3 + 4x4
= -
1
2х] + Зх
2
- 6x3 - Х4 = -2
2х| - х
2
- 6x3 + ЗХ4 = -2 .
4.
\
Зхі - 2х
2
- ЗХ3 + ЗХ4
=
~4 ,
х, + 2х
2
- 2х
3
- 2x4
= 4
'
X] - х
2
- 2x3 + Х4 = -2 ;
2х] + х
2
- 4x3 - Х4 = 2 .
Зх] - х
2
- 5хз + 5x4
=
1 '
2х] + х
2
- 5хз = -1 ;
Х|
- 2х
2
+5x4= 2 ;
X]
+
Х
2
-ЗХз-
Х4
= -1.
2х] + х
2
+ Х3 + 2х
4
= 3 ;
X] + 2х
2
- х
3
+ х
4
= -3 ;
Х| + Зх
2
- х
4
= 0 ;
Зх| + 4х
2
+ 2х
3
= 6 .
х
\
+ 2х
2
- ЗХ3 -6х
4
=
4;
X, -4х
2
-Зх
3
=
-8;
X, - 2х
2
- Зхз -2х
4
=
- 4 ;
2х| -5х
2
-6x3 -Зх
4
= -10
2х[ + х
2
- Х3 = 7 ;
Хі - Зх
2
+ х
3
- Зх
4
= 0 ;
2х
2
+ Х3 - 2x4
=
2 ;
Зх( - х
3
- Х4 = 9 .
69
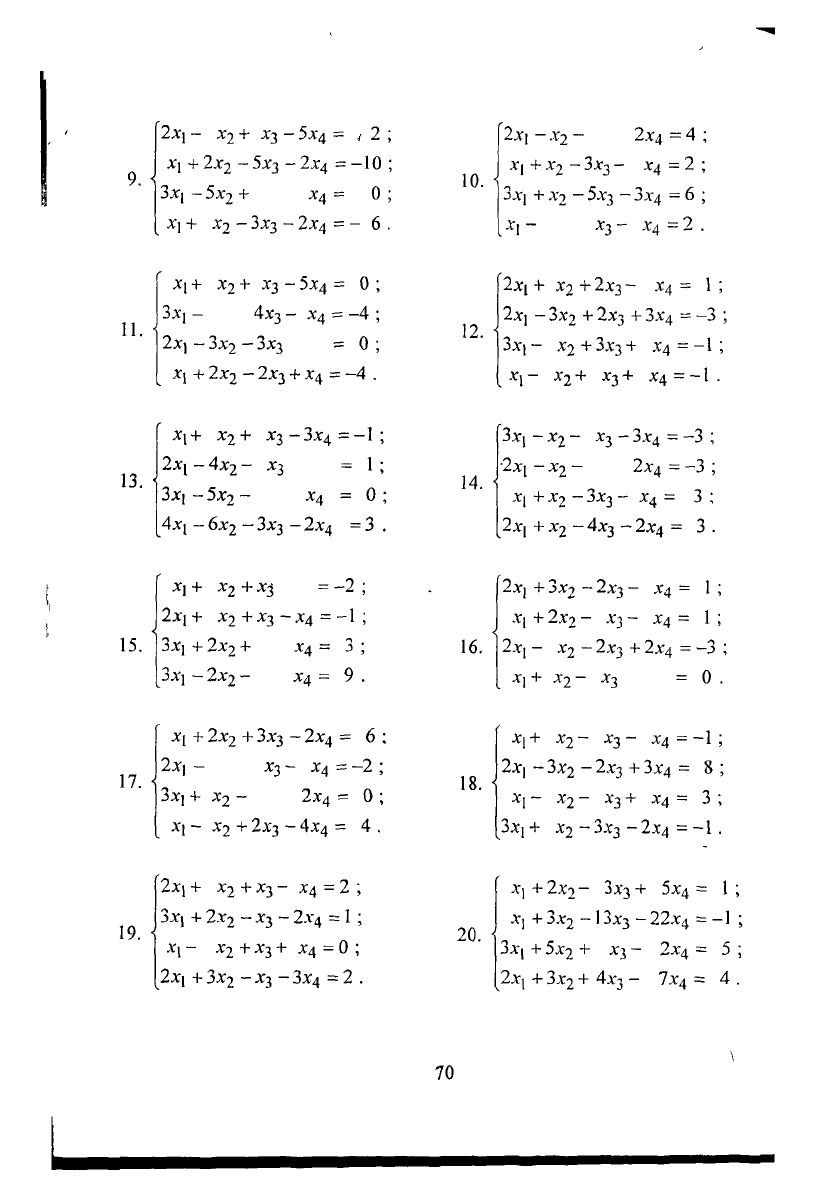
9. і
2дГ]
- х
2
4- х
3
- 5х
4
= і 2
х\
+
2х
2
- 5х
3
- 2х
4
= -10
Зх[ - 5х
2
+ х
4
= 0
X]
+ х
2
- Зхз - 2х
4
= - 6
10.
^
2х] - х
2
- 2х
4
= 4
Х|
+ х
2
- Зх
3
- х
4
= 2 :
Зхі + х
2
- 5*з - Зх
4
= 6 ;
[х, - х
3
- х
4
= 2 .
11.
X)
+ х
2
+ хз - 5х
4
= 0
Зх] - 4х
3
- х
4
= -4
2х| - Зх
2
- Зх
3
= 0
X!
+ 2х
2
- 2х
3
+ х
4
= -4
12.
2х[ + х
2
+ 2хз - х
4
= 1 ;
2х[ - Зх
2
+ 2х
3
+ Зх
4
= -3 ;
Зх]-
х
2
+ 3хз+ х
4
= -1;
X)
- х
2
+ х
3
+ Хц = -1 .
13.
х
\
+ х
2
+
*
3
-3х
4
=-1
2х, - 4х
2
- х
3
=1
Зх, - 5х
2
- х
4
= 0
4х
(
- 6х
2
- Зх
3
- 2х
4
= З
14.
Зх,
—
х
2
—
х
3
—
Зх
4
—
—3
;
2х| - х
2
- 2х
4
= -3 ;
Х|
+ х
2
- Зх
3
- х
4
= 3 ;
2х| + х
2
- 4х
3
- 2х
4
= 3 .
15.
х
\
+
х
2
+
Х
І
= -
2
2хі + х
2
+х
3
-х
4
= -1
Зх, + 2х
2
+ х
4
= З
Зх] - 2х
2
- х
4
= 9
16.
2х, + Зх
2
- 2х
3
- х
4
=
1
;
Х|
+ 2х
2
- х
3
- х
4
= 1 ;
2х| - х
2
- 2х
3
+ 2х
4
= -3 ;
X]
+ х
2
- х
3
= 0 .
17.
Х[
+ 2х
2
+ Зх
3
- 2х
4
= 6
2х| - х
3
- х
4
= -2
Зх] + х
2
- 2х
4
= О
X)
- х
2
+ 2х
3
- 4х
4
= 4
18.
Х|
+ х
2
—
х
3
—
х
4
—
—1
;
2х\ - Зх
2
- 2х
3
+ Зх
4
= 8 ;
Х\ - х
2
- х
3
+ х
4
= 3 ;
Зх[+ х
2
-Зх
3
-2х
4
=-1 .
19.
2Х)
4- х
2
4- х
3
- х
4
= 2
Зх)
4-
2х
2
- х
3
- 2х
4
=
1
*1
_
Х
2
4-
Х
3
4-
Х
4
=
О
2х[
4-
Зх
2
- х
3
- Зх
4
= 2
20.
Х)4-2х
2
-
Зх
3
4-
5х
4
= 1;
X]
4-
Зх
2
-1 Зх
3
- 22х
4
= -1 ;
Зх
(
4-
5х
2
4- х
3
- 2х
4
= 5 ;
2х,
4-
Зх
2
4-
4х
3
- 7х
4
= 4 .
70
