Тевяшев А.Д., Литвин О.Г. Вища математика. Загальний курс: Збірник задач та вправ
Подождите немного. Документ загружается.

2х,
2х
Зх
2х
'2х
4х
2х
Х\
2х
Зх
27.
29
X]
X
2х,
х
\
2-Ї,
4х
]
4х,
2х
]
2х,
4х,
6Х|
8х
— х
2
+ х^
—
х
4
—
1 ;
— х
2
—
Зх
4
= 2 ;
— х
3
+ х
4
= -3 ;
+ 2х
2
- 2хз + 5х
4
= -6 .
+ х
2
- хз - Зх
4
= 2
+ хз - 7х
4
= З
2х
2
- Зх
3
+ х
4
= 1
+ Зх
2
- 4х
3
- 2х
4
= З
-4х
2
+2х
3
= -1 ;
- Зх
2
- хз - 5х
4
= -7 ;
- 7х
2
+ х
3
- 5х
4
= -8 ;
х
2
—
Х3
—
х
4
= — 1 .
- х
2
+ Х3 — х
4
= — 2
+ 2х
2
- 2хз - х
4
= - 5
- х
2
- Зхз + 2х
4
= - 1
+ 2х
2
+ 2х
3
- бх
4
= -10
+ 5х
2
+ х
3
+ Зх
4
= 2 :
+ бх
2
+ Зхз + 5х
4
= 4 ;
+ 14х
2
+ х
3
+7х
4
=4 ;
- Зх
2
+ Зх
3
- х
4
= 7 .
- х
2
+ Зхз + 4х
4
= 5
- 2х
2
+ 5х
3
+ 6х
4
= 7
- Зх
2
+ 7х
3
+ 8х
4
= 9
-4х
2
+9х
3
+10х
4
=11 .
22.
24.
26.
4
28.
\
30.
х\
- 2х
2
+ Зхз - 4х
4
= 4 ;
х
2
—
х
3
+ х
4
=
—3
;
х\
+
Зх
2
- Зх
4
= 1 ;
- 7х
2
+ Зхз + х
4
= -3 .
Х| + Зх
2
+ 5х
3
- 2х
4
= З
2х| + 7х
2
+ Зхз + х
4
= 5
Х| + 5х
2
- 9х
3
+ 8х
4
= 1
5х] + 18х
2
+4х
3
+5х
4
= 12
2х]
+ Зх
2
- хз + х
4
=
1
8х] + 12х
2
- 9х
3
+ 8х
4
= З
4х| + 6х
2
+ Зхз - 2х
4
= З
2х] + Зх
2
+ 9х
3
- 7х
4
= З
4хі + х
2
- 2хз + х
4
= З
X] - 2х
2
- хз + 2х
4
= 2
2х| + 5х
2
- х
4
= -1
Зх[ + Зх
2
- хз - Зх
4
= 1
Х\ + Зх
2
- 2хз + 2х
4
= -4
5х] + 4х
2
+ хз + Зх
4
= -5
2х! + х
2
+ х
3
+ 4х
4
= 2
Зх] + 2х
2
+ хз + х
4
= -З
71

Задача 5. Знайти власні значення і власні вектори матриці
Варіанти завдань
(\ 2
-2Ї
' 2
-1 0^
ґ
з
-1 1
1.
1 0
3
2.
-1
2
0
3.
0
2
-1
^
3
°У
V
-1
1
)
,о -1
2
(5 -1 -0
/ 5
-2 -і
' 3
1
-
4.
0 4 -1
5.
-1
5 -і
6.
2
2
-
V 1
-2 4
У
,-2
1 4
' 2 0
Г 2
1
°1
Г
4
1
°)
7.
1 1 -
8. 1 2
0
9.
1
4
0
0
2^
V
1
1
\
1
( 5 1
-
Г
-4
(
0
1 о
ч
10.
-2 4
-
і
11.
2
1 2
12.
-4 4 0
,-
2 1
6
І
2
0
Ь
,-2
1
2,
г
3 -2
2
Л
Ґ5
-2
2^
(1
-4
4'
13.
0 3 0
14.
0
5 0
15.
2
2
^0 2
,°
2
->
,2
0
ґ
7 -6 6^
(1
-6
~ь\
^13
2
_
16.
4 -1
4
17.
2
3
2
18.
6 9
-
,4 -2
5
,
І
2
2
3
,
,2
-2
'4 -1
0
'4 -5
2^
'-\
3 -1
19.
3 1 -1
20.
5
-7
->
3
21.
-3 5
-1
,1 0
1
)
V
6
-9
Ь
V"
3
3
1
У
У
У
72

Го
-4
0'
\
Г
4
2 6
(2 1 -
22.
1
-4 0
23.
2
1
3
24.
1 2
-
і
-2
/
-3
9
)
0
^ 0
°1
0
°]
'б
1
-
25.
1 2
-1
26.
1
4 --1 . 27. 2 5
-2
-1
2
>
-1
4
,
.1
-1
4,
'1
-1
Г-і
0
1^
' 7
4
-
2
28.
1 1
-1
29.
1 -1
0
зо.
-2 5 -
2
-1
2,
4
-
ь
0 9
-3
31.
і 2
1
1 2
2.5. Зразок виконання індивідуального завдання 2
Задача 1. Обчислити визначник четвертого порядку :
;>
1 2 -1
2 1 0 -2
1 2
1
2
2 -3
1
2
Розв'язання. Використаємо метод пониження порядку , оснований
на застосуванні теореми розкладання визначника за елементами деякого
рядка (стовпця) . При цьому заздалегідь , використовуючи властивості
визначника, обертаємо в нуль усі, окрім одного , елементи його деякого
рядка (стовпця).
Виконаємо , наприклад , наступні перетворення.
Другий рядок помножимо послідовно на (-1), (-2), 3 і додамо до
першого, третього, четвертого рядків відповідно.
73

Отриманий визначник розкладемо за елементами другого стовпця
А =
10 2 1
2 10-2
-3 0 1 6
4 0 1 4
,2+2
1 2 1
-З 1 6
4 1 4
Далі знов обертаємо в нуль усі елементи першого стовпця, окрім еле-
мента в лівому верхньому куті, і після цього обчислюємо визначник другая
-
порядку або використовуємо для обчислення отриманого визначника третьо-
го порядку правило трикутників :
Д =
2
7
-7
7 9
-7 0
= 63
Обчислення за правилом трикутників має такий вигляд :
1 2 1
6 =4-3 + 48-4-6 + 24 = 63 . -З
4
Відповідь : Д = 63
Задача 2. Знайти значення многочлена / (х) при х = А , де /1
задана матриця :
Ґ
\ -2 -3^
/(х) = 2х
2
+Зх-5 , А-
4 0
З 2
-1
0
Розв'язання. /(А) = 2А
2
+ЗА-5Е , де £ - одинична матриця
третього порядку :
'\ -2 -З
4
(\ -2
-з"!
Ґ
\ -2
~
3
1
'1 0 0^
ЛЛ)
=
2
4 0-1
4
0 -і + 3 4 0 -1 -5 0 1 0
,3 2 0,
,з
2
о,
,3 2
о
1,
74
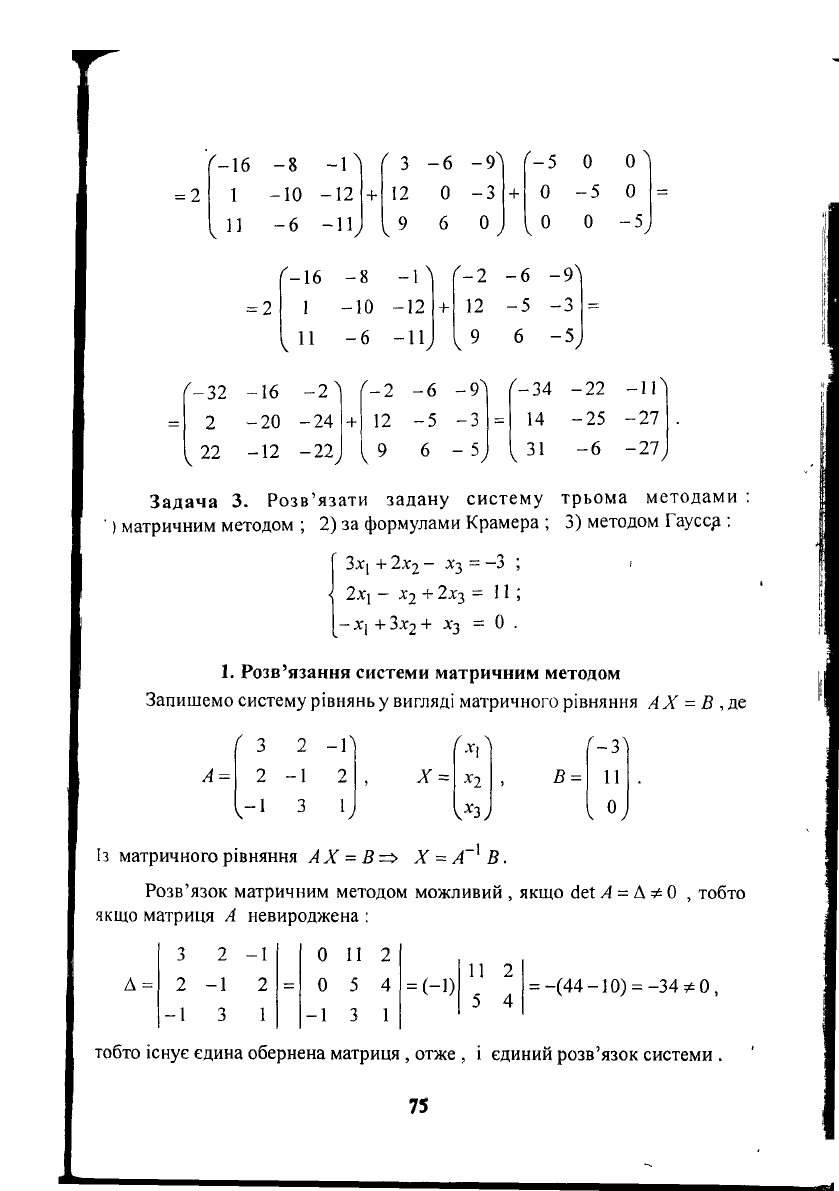
= 2
-16
1
11
-8 -1
-10 -12
-6 -11
= 2
•16
11
-10
-6
3 -
-6
-9
2
0 -3
9
6
0
-0
'-2
-12
+
12
"Ну I
9
Л ґ
+
-5 0
0 -5
0 0
О
-5
•9^
-З
"5,
'-32
2
V
22
-16 -2Ї
-20 -24
-12 -22
-2 -6 -9"і
12 -5
9 6
'-34 -22
14 -25
31 -6
-11
-27
-27
Задача 3. Розв'язати задану систему трьома методами :
матричним методом ; 2) за формулами Крамера ; 3) методом Гаусса :
Зх, + 2х
2
- х
3
= —3
; і
2х[ - х
2
+ 2х
3
=11;
- Х| + Зх
2
+ хз = 0 .
1.
Розв'язання системи матричним методом
Запишемо систему рівнянь у вигляді матричного рівняння А X - В , де
( 3 2
-0
(V
(~
3
)
А = 2 -1 2
х =
х
2
в =
11
-1
3
1
)
3,
і о,
Із матричного рівняння А X = В :
Розв'язок матричним методом можливий , якщо сієї Л = А ф 0 , тобто
якщо матриця А невироджена :
2
11 2
= -(44-10) = -34*0,
5 4
тобто існує єдина обернена матриця , отже , і єдиний розв'язок системи .
3 2 -1
0
11
2
А = 2 -1 2
=
0 5 4
= (-1)
-1 3 1
-1 3 1
75

Знайдемо обернену матрицю А
^=1^
=
1
11 Л
2
1
А
з\
12
А 22
А
32
13
А
23
Л
33
де А
д
=(-і)'
+
^-М
у
, 1<і,]<3
Знайдемо алгебраїчні доповнення
-1 2
З 1
=
-7,
Л.2 = ~
2 2
-1 1
= -4
'13
= 5 ;
А
21
=-
2 -1
3 1
= -5
^22 =
З -1
-1 1
= 2
^23=-
3 2
-1 З
= -11.
Перевіримо правильність знаходження оберненої матриці шляхом пе-
ревірки виконання рівності А А"
1
= Е :
АА~
[
=
_\_
34
З
2
-1
'-34
0
0
2 -1
Л
-1 2
З 1
0
-34
0
34.
0
Л
0 =
-34,
-7 -5 3
Л
-4 2 -8
5 -11 -7,
Л 0 0
х
!
0 1 0
0 0 1
= Е.
)
76

Перевірка показує , що обернена матриця знайдена вірно
Х = А~
х
.В
=
-±-
'-1 -5
3^
(
-3
Х = А~
х
.В
=
-±-
-4
2 -8 11
34
V
5
-11
-\
V
0
_1_
34
_1_
34
Г-34^
(
Г
34 =
-1
,-136
у
,
4
,
V
21-55 + 0^1
12 + 22 + 0
-15-121 + 0
Хі = 1, х
2
= -1, Хз = 4 .
Перевірка правильності розв'язку.
Підставимо отриманий розв'язок у систему :
З•
1
+ 2•(-1)-4 = -3 ;
• 2-1-(-і)+2-4 = 11 ;
-1 + 3-(-і)+4 =0 .
Система розв'язана вірно .
Відповідь : х\ =
1
, х
2
=-1 ,
Х3
= 4 .
2.
Розв'язання системи за формулами Крамера
сієї А = А = -34
Ф
0 => існує єдиний розв'язок системи .
Формули Крамера мають вигляд :
х
з
_А
3
де А,, / = 1, 3 одержується із визначника Л системи шляхом заміни і -го
стовпця стовпцем вільних членів :
-З
11
0
-з
11
о
5
-7
0
-З
11
: 21-55 = -34 ;
77

3 -3 -1
3 -3 2
2 11 2
= 2 11
4
-1 0
1
-1 0
0
3
2
-3
3
11 -3
А
3
=
2 -1 11
=
2
5-
11
-1 3 0 -1
0 0
* А,
-34
-34
=
1
,
х
2
А
-З 2
11 4
= -(-12-22) = 34 .
11 -З
5 11
= -(і21 + 15)=-136.
34
А
3
-136
-34
3.
Розв'язання системи методом Гаусса
Запишемо розширену матрицю системи і приведемо її до трикутногс
вигляду за допомогою елементарних перетворень матриці, які виконуютьсі
над рядками:
А =
-1
2-12
-1 3 1
(-1 3 1
2-12
3 2-1
11
-1 3 1
0 5 4
0 11 2
0
11
-З
3 1 0 > 3 1
0 >
3 1 0 ^
0 5 4 11
~
0
1 -6
-25 0
1
-6
-25
1
-6
-25;
,0 5
4
11
;
1°
0 -34
-136,
і-\ з
0 1
ч
о о 1
о
-25
4
К§Л = К.§/1 = 3 = и, де п - число невідомих .
Система сумісна , має єдиний розв'язок .
Ставимо у відповідність розширеній матриці систему , еквівалентну
вихідній , розв'язання якої.здійснюємо знизу уверх :
78

-
лг|
+ Зх
2
+
х
3 ~ 0 ;
х
2
~
= _
25 ; <=>
*3
=
4
,
х, = 3x2 + х
3
=-3 + 4 =
1
;
дг
2
=-25 + 6дг
3
=-25 + 24 =-1 ; о
х
3
= 4 ;
*1
= 1 ;
х
2
= -і;
х
3
= 4 .
Задача 4. Дослідити сумісність системи , і у випадку сумісності знай-
I
т» загальний розв'язок та один частинний розв'язок системи . Виконати пе-
I
згаірку
правильності частинного розв'язку :
Х\ + *2 - 7х
3
- 2*4 = -1
-х\+ 2x2 ~ 5х
3
- 7*4 = -5
2х\ +
дг2
_
Юдг
3
-
*4 = 0
-Зх
1
+2дг
2
+ л:
3
-9х
4
=-7.
Розв'язання. Запишемо розширену матрицю системи і за допомогою
пементарних перетворень , що виконуються над рядками матриці, приве-
демо її до східчастого вигляду :
'
1
1 -7
-2
!
-Г
'1
1 -
7
-2
і
-Г
-1
2 -5
-7
-5
0 3
-12
-9
і
-6
2 1 -10
-1 0 0
-1
4
3
|
2
.-з
2
1
-9
-ь
,о
5
-20
-
15
! -
-10,
Ґ1
1 -7 2
-Г
(\
1 -7 -2
і "
Г
0
1 -4
-3
-2 0
1 -4 -3
і -2
0 1 -4 -3 -2
0 0 0 0
і
0
,о
1
-4 -3
"2,
,0
0 0 0
!
0,
Замітимо, що при приведенні до східчастого вигляду можлива також
переміна місцями стовпців, що відповідає перепозначенню змінних .
Отримали:
Я§Л = К§Л = г = 2<4 = и, я - число змінних . Згідно з теоремою Кроне-
кера - Капеллі система сумісна ; система має безліч ріозв'язків , бо г < я . Роз-
в'язання здійснюємо методом Гаусса . Базисні змінні - х\ , х
2
; вільні змінні
х
3
. *4 •
СІ'авимо у відповідність перетвореній розширеній матриці системи
79

скорочену систему, яку розв язуємо знизу уверх :
Гх| + х
2
- 7х
3
- 2x4
= _
1
>
\
х
\ +
х
2
=
7^з
+
2*4 ~
1 >
1
х
2
-4х
3
-ЗХ4
=-2 , 1 х
2
=4х
3
+3х
4
-2 ,
Х|
= -х
2
+ 7х
3
+ 2х
4
-1 = -4х
3
-
ЗХ4
+ 2 + 7х
3
+ 2х
4
-1
х
2
= 4хз + Зх
4
- 2 ,
X]
= Зх
3
— Х4
+11
[х
2
= 4х
3
+ Зх
4
- 2, х
3
, х
4
є К.
Запишемо загальний розв'язок у вигляді
^Зх
3
- х
4
+ Р
4хз + Зх
4
- 2
*з
х
4
Х(х
3
,х
4
) =
де х
3
, х
4
є К .
Нехай, наприклад , х
3
= 0 , х
4
= 0 . Отримаємо частинний розв'язок
*(о,0)
=
-2
0
V
Ь
тобто Х[ = 1, х
2
= -2 , х
3
= 0 , х
4
= 0 .
Перевірка. Підставимо отриманий частинний розв'язок у систему :
1-2
—0 —0
= -1 ;
-1-4-0-0 =-5;
2-2-0-0= 0;
-3-4 + 0-0 = -7 .
Система розв'язана вірно .
80
