Бороденко В.А. Исследование систем управления в среде MATLAB

Подождите немного. Документ загружается.

101

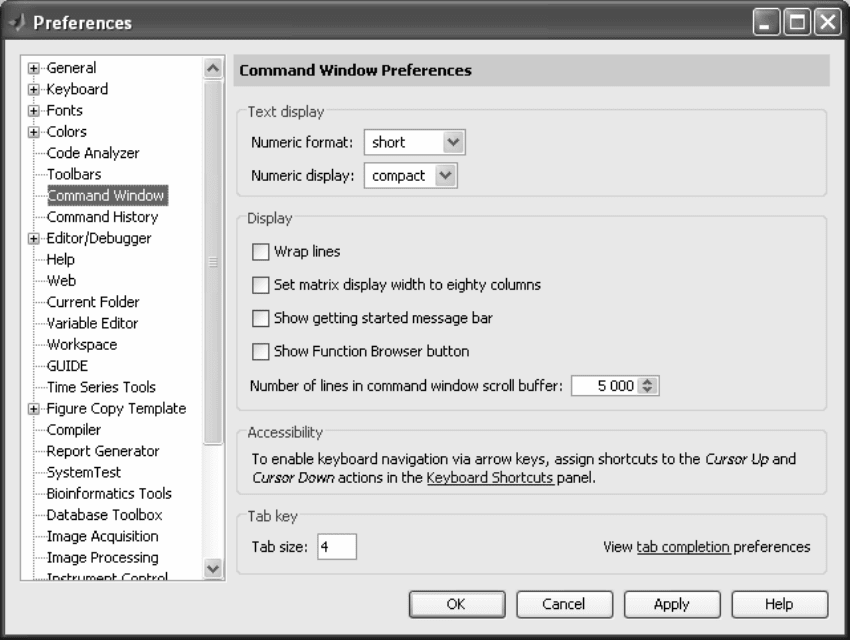
File-Preferences-Fonts увеличить размер шрифта Monospace/Plain с 7

до 10 или 11.

Рисунок 2.3

По ходу вычислений все записи в командном окне смещаются

вверх и становятся неактивными – их можно скопировать, но нельзя

исправить и запустить повторно. Активной является лишь командная

строка с приглашением >>, справа от которого мигает курсор. Сюда

вводятся команды, ввод завершается клавишей Enter. Во время ввода

той или иной функции появляются подсказки формата ввода.

По ходу сеанса программа ведет журнал операций (Command

History), открыв который, использованные ранее команды можно вы-

зывать повторно. Вставлять команды в рабочую строку можно и ско-

пировав их из какого-либо текста, например, сохранив их ранее в фор-

мате документа MS Word. Клавиши управления курсором вверх-вниз

вызывают предыдущие операции (строки) по журналу команд, клави-

ши управления влево-вправо позволяют перемещаться по командной

строке. Команда вводится нажатием клавиши Enter при любом поло-

жении курсора в командной строке. Сохранить все данные текущего

сеанса позволяет команда File-Save Workspace as…

102

Основной режим работы программы MATLAB – прямые вычис-

ления (режим интерпретатора). Минимальный рабочий элемент –

комплексная матрица, размеры массивов и тип данных можно не ука-

зывать. Обработка производится по строкам, в одной строке допуска-

ется несколько операторов, разделенных запятой или точкой с запя-

той, перенос длинной строки осуществляется знаком троеточия ... Ес-

ли в конце строки нет точки с запятой, сразу выводится результат или

значение описанной переменной (выражения). Числа выводятся в не-

скольких форматах по выбору (по умолчанию Short), вычисляется все-

гда 16 значащих цифр в диапазоне от 10

-308

до 10

308

. При выводе мо-

жет быть выбран интервал между строками (по умолчанию увеличен-

ный Loose). Различаются прописные и строчные символы, функции

вводят строчными (маленькими) буквами. Общая справка вызывается

командой help, справка по конкретной функции или оператору коман-

дой help имя_функции, например, help ops.

Программа использует системные переменные и константы –

величины с собственным именем (идентификатором), значения кото-

рых предустановлены:

ans – результат последней операции без знака присваивания (его

можно использовать в выражениях, пока не произошло изменение);

eps – относительная точность дробного числа, равна 2

-52

2.2204e-016;

pi – число π = 3.14159265358979;

realmin – наименьшее вещественное число 2

-1022

= 2.2251e-308;

realmax – наибольшее вещественное число 2

1022

= 1.7977e+308;

intmin – наименьшее целое число -2147483648;

intmax – наибольшее целое число 2147483647;

Inf – бесконечность (Infinity);

NaN – не число (Not a Number), неопределенность (результат

операций типа 0/0 или Inf-Inf и т. д.);

i, j – обозначения мнимой единицы

1

. Ввод комплексного

числа производится в форме a = -1+0.3i, a = -1+0.3j или a = -1+ i*0.3,

a=-1+j*0.3.

Значения системных переменных могут быть переопределены в

пределах одной сессии и восстановлены командой clear, например

>> realmin

ans =

2.2251e-308

>> realmin=0.1

realmin =

0.1000

>> clear; realmin

103

ans =

2.2251e-308

Оператор who вызывает список всех переменных в Workspace,

оператор whos – таблицу имен и описаний переменных, оператор

clearvars удаляет все переменные из Workspace. Возможен показ или

удаление только перечисленных переменных whos var1 var2 (нельзя

вместо пробела использовать в качестве разделяющего знака запятую,

хотя в других случаях они равноценны), только переменных, начи-

нающихся на определенный символ, например, who a*. Оператор clear

variables удаляет только переменные, в форме clear all удаляет также

глобальные переменные, функции и связи.

MATLAB ограничивает набор символов, допустимых для имен

переменных и файлов, длина имен переменных пользователя не долж-

на превышать 63 символа. Особые символы:

>> – приглашение к работе;

= – знак присваивания;

% – предваряет комментарий;

'(апостроф) – кавычки для текста или строковых переменных,

символ транспозиции;

точка – разделитель десятичной части дробного числа;

точка с запятой – отменяет немедленный вывод результата на

экран;

[ ] – назначить, например P=[1 2 3 4] – назначить коэффициенты

полиному Р, обозначение векторов и матриц;

( ) – от аргумента (используя), например, вычислить корни

roots(P) от полинома Р;

{ } – выделение подсистем, групп однотипных массивов;

пробел и запятая – объединение (конкатенация) по горизонтали;

клавиша Enter (при наборе данных) или точка с запятой – объе-

динение (конкатенация) по вертикали, так при задании матрицы раз-

деляются строки A = [1 2; 3 4].

Функция – это слово (имя) со скобками, в которых записывают-

ся аргументы функции, т. е. величины, от которых зависит результат,

возвращаемый функцией. Оператор обозначает действие, которое не-

обходимо проделать. Например, оператор disp печатает запись справа

от него, как текст, функция disp() позволяет показать результат без

присвоения его значения переменной аns:

>> disp 2-7

2-7

>> disp(2-7)

-5

104

Оператор format устанавливает текущее значение интервала ме-

жду строками при выводе (loose – больше, compact – меньше) и спо-

соб вывода чисел: short – пять цифр с фиксированной точкой; short е –

пять цифр с плавающей точкой; long – 15 цифр при двойной, семь

цифр при одинарной точности с фиксированной точкой; long е – то же

с плавающей точкой; short g, long g – то же, с выбором наилучшего

способа представления.

По формату format rat выводятся числа в виде рациональной

дроби с целыми числителем и знаменателем, использование оператора

format без дополнений восстанавливает первоначальные установки.

>> pi

ans =

3.1416

>> format rat; pi

ans =

355/113

>> format; pi

ans =

3.1416

Не во всех случаях использование оператора приводит к изме-

нению способа вывода чисел – многие функции, например, функция

damp(), имеют свой собственный неизменный формат вывода.

2.2 Элементарные операторы и функции

Операторы и функции проверки отношений:

== или eq() равно;

~= или ne() не равно;

> или gt() больше;

< или lt() меньше;

>= или ge() не менее;

<= или le() не более.

Если отношение выполняется, результатом является логическая

единица, если не выполняется – нуль:

>> eq(2,5)

ans =

>> eq(2,2)

ans =

>> 2==2

ans =

105

Функции проверки типа объекта:

isscalar() истина для скалярной величины;

isvector() истина для векторной величины;

isrow() истина для вектора-строки;

iscolumn() истина для вектора-столбца;

ismatrix() истина для матрицы;

isnan() истина для неопределенности Not-a-Number;

isinf() истина для бесконечности;

isfinite() истина для конечного элемента.

Арифметические операторы и функции:

( ) изменение порядка вычислений скобками;

+ или plus(a,b) сложение a+b;

- или minus(a,b) вычитание a-b,

uplus() и uminus() присвоение знака плюс (минус) числу;

* или mtimes(a,b) умножение a*b;

/ или mrdivide(a,b) деление слева направо, так, 2/5 = 0.4;

\ или mldivide(a,b) деление справа налево, так, 2\5 = 2.5;

^ или mpower(a,b) возведение в степень a^b, например

>> mpower(2,3)

ans =

Логические операторы и функции:

& или and() И;

&& укороченное А И В, когда при А=0 проверка В

не производится;

| или or() ИЛИ;

|| укороченное А ИЛИ В, когда при А=1 про-

верка В не производится;

~ или not() НЕ;

xor() ИСКЛЮЧАЮЩЕЕ ИЛИ;

any() истина, если хотя бы один элемент массива не

ноль;

all() истина, если все элементы массива не ноль.

Тригонометрические функции – приведем лишь некоторые,

справку по остальным можно получить командой help elfun (элемен-

тарные функции):

sin() и sind() синус угла, заданного в радианах и градусах;

asin() и asind() угол по его синусу, возвращается в радианах и

градусах;

106

cos() и cosd() косинус угла, заданного в радианах и граду-

сах;

acos() и acosd() угол по его косинусу, в радианах и градусах;

tan() и tand() тангенс угла, заданного в радианах и градусах;

atan() и atand() угол по его тангенсу, в радианах и градусах;

atan2(Re, Im) выводит результат для всех четырех квадран-

тов комплексной плоскости в радианах при вводе двух аргументов –

действительной Re и мнимой Im частей.

Экспоненциальные функции:

exp() степень натурального числа е;

log() натуральный логарифм;

log10() логарифм по основанию 10;

log2() логарифм по основанию 2;

pow2() степень двух, например, pow2(3) = 8;

sqrt() квадратный корень, например, sqrt(-4) = 0 + 2.0000i;

realpow() степень действительного числа;

reallog() натуральный логарифм действительного числа;

realsqrt() корень квадратный из неотрицательного числа;

nthroot() корень n-ой степени из вещественного числа.

Функции округления и вычисления остатков:

fix() округление к нулю;

floor() округление к минус бесконечности;

ceil() округление к плюс бесконечности;

round() округление к ближайшему целому;

mod() остаток от деления с учетом знака;

rem() остаток от деления;

sign() знак числа.

Функции обработки данных (остальные по справке help datafun):

max() максимальный элемент массива (и его индекс);

min() минимальный элемент массива (и его индекс);

mean() среднее значение элементов вектора;

median() срединное значение элементов вектора;

sum() сумма элементов вектора или колонок матрицы;

prod() произведение всех элементов вектора (вектор-строка

произведений элементов колонок матрицы);

mode() наиболее частое значение в наборе;

std() стандартное отклонение;

var() вариация;

sort() сортировка элементов в порядке возрастания.

Особенностью применения функций в MATLAB является то,

что возвращаемый результат зависит от числа передаваемых парамет-

107

ров и вида обращения, например, возможны варианты plot(y), plot(x,

y) и plot(x1,y1,x2,y2). Обычно выводится столько элементов результа-

та из разрешенного количества, сколько аргументов перечислено в

квадратных скобках левой части равенства – по умолчанию при от-

сутствии левой части выводится лишь первый элемент из возможного

количества, либо график.

Следует помнить, что встроенные функции и операторы могут

вести себя не совсем обычно с учетом того, что минимальным элемен-

том MATLAB является комплексная матрица, в то же время матрицы

и массивы здесь не одно и то же.

2.3 Специальные операторы и функции

В операциях с комплексными числами используются:

real() выделение действительной части числа, Re = real(y);

imag() выделение мнимой части числа, Im = imag(y);

abs() модуль числа

ImRe  или sqrt(re.^2+im.^2);

angle() аргумент числа, arctg(Im/Re), в радианах, от - до

+ (аналог функции atan2);

conj(a) комплексная величина

, сопряженная к а (аналог

сопряженного транспонирования a’);

complex(a,b) композиция комплексного числа a + jb из двух ве-

щественных чисел;

cplxpair(v) собирает комплексные величины вектора v в сопря-

женные пары с возрастанием действительной части, потом мнимой

части, действительные числа помещаются в конец списка;

esort(v) сортировка элементов вектора комплексных чисел v

по убыванию значения их действительных частей; в сопряженных па-

рах первой идет величина с положительной мнимой частью;

unwrap(phi) непрерывное изменение фазового угла phi (в про-

тивном случае угол удерживается в диапазоне -180...+180 град;

isreal() истина для массива вещественных чисел.

Многочлены вида a

+ a

n-1

+ … + a

n+1

вводятся своими ко-

эффициентами P = [a

… a

n+1

] в квадратных скобках через пробел

или запятую в порядке убывания степени переменной как вектор

(первый индекс равен единице, ни один коэффициент не пропускает-

ся). Действия с полиномами:

+ или plus(P1, P2) сложение полиномов равного размера;

- или minus(P1, P2) вычитание полиномов равного размера;

conv(P1, P2) умножение полиномов (операция сверт-

ки);

108

deconv(P1, P2) деление P1 на P2; с левой частью произ-

водится деление с вычислением остатка [Q, R]=deconv(P1, P2), где Q –

частное, R – полином остатка;

roots(P) вычисление корней полинома Р;

poly(R) построение полинома по вектору корней R,

либо вывод характеристического многочлена матрицы R;

polyval(P,x) значение полинома Р(x) при заданной вели-

чине переменной x, которая может быть и комплексной;

polyder(P) значение коэффициентов производной от по-

линома Р

polyfit() подбор полиномиального выражения для на-

бора данных.

polyeig() вычисление собственных значений и векторов

для совокупности квадратных матриц;

polyint(Р) значение коэффициентов интеграла от поли-

нома Р;

polyvalm(Р,Х) значение полинома при заданной величине

матричного аргумента x (n×n) и вектора коэффициентов Р

Y = P(1)*X^N + P(2)*X^(N-1) + ... + P(N)*X + P(N+1)*I;

residue(num, den) разложение отношения двух полиномов num,

den на простые дроби.

Векторы задаются как вектор-строка V=[1 2 3], вектор-столбец

V=[1; 2; 3] или V=[1 2 3]' и вычисляемый вектор. Последнему соот-

ветствуют:

- линейная прогрессия V=1:0.1:10 – в примере от 1 до 10 с шагом

0.1, т. е. 100 точек (шаг вектора V=1:10 по умолчанию равен 1) или

v=linspace(1,10,100);

- логарифмический масштаб V=logspace(-2,2,100) – от 10

-2

до

, всего 100 точек. Если число точек не указано, по умолчанию оно

принимается равным 50.

Векторизация позволяет отказаться от использования циклов.

Например, создадим таблицу десятичных логарифмов от 1 до 2 с ша-

гом 0.1

>> x=(1:0.1:2)'; logs=[x log10(x)]

Ввод матрицы производится по строкам A=[1 2 3;4 5 6;7 8 9] или

поэлементно A(1,1)=1; A(3,3)=9 или A(1)=1; A(2)=4; A(9)=9 (одиноч-

ный индекс отсчитывается по столбцам). Первый индекс указывает

строку, второй – столбец, начальный индекс 1. Размер матрицы опре-

деляется автоматически по элементу с наибольшим индексом, необо-

109

значенные элементы внутри установленной размерности автоматиче-

ски обнуляются (не действует для функции reshape).

>> w(2,4)=-1.234

w =

0 0 0 0

0 0 0 -1.2340

>> w(8)

ans =

-1.2340

Задав блоки v1=[1 2], v2=[3 4], можно образовать матрицу из

них А=[v1;v2]. Часть матрицы описывается через индексы с помощью

двоеточия, например, A(1:k,j) – столбец j, строки с 1 по k. Слово End

обозначает последний столбец (строку). В MATLAB легко изменяют-

ся размеры матриц удалением (добавлением) строк или столбцов. Так,

использование пустой (Empty) матрицы (вектора) A(:,2)=[ ] удаляет

все элементы второго столбца матрицы А, при этом число столбцов

уменьшается на единицу.

Открыв окно Workspace и дважды щелкнув мышью имя масси-

ва, можно вызвать редактор массивов Array editor, который позволяет

быстро изменить данные любой ячейки выбранного массива. Здесь

же, использовав инструмент Plot Selection, по данным массива можно

построить один из видов графиков (plot, bar, imagesc, contour и т. д.).

В MATLAB автоматически формируются и вычисляются (пол-

ная справка выводится по команде help elmat):

zeros(n) квадратная нулевая матрица размера n;

eye(n) квадратная единичная матрица размера n;

ones(n) квадратная матрица размера n из одних единиц;

diag(A) вектор-столбец из элементов главной диагонали

матрицы A, либо диагональная матрица из вектора-столбца А;

A' комплексно сопряженное транспонирование матри-

цы A, соответствует функции ctranspose();

inv(A) обратная к А матрица (аналог А^-1);

balance(A) сбалансированная А с примерно равными нормами

по строке и столбцу, [T, B]=balance(A) с матрицей преобразования Т;

det(A) определитель матрицы А;

trace(A) след матрицы А (сумма элементов главной диаго-

нали);

rank(A) ранг матрицы А (порядок наибольшего ненулевого

минора);

poly(A) характеристический полином матрицы А вида

P(s)=det(s∙1-A), где 1 – единичная матрица;

110

eig(A) вектор-столбец собственных значений матрицы А;

при обращении [T, Ad]=eig(A) выводит модальную форму Ad (с ком-

плексными собственными значениями на главной диагонали) матрицы

А и сбалансированную матрицу собственных векторов Т;

svd(A) сингулярное разложение m×n матрицы А = USV

где диагональная m×n матрица S содержит положительные сингуляр-

ные величины σ

> σ

> ... > 0 матрицы А, а столбцы ортогональных

матриц U (m×m) и V(n×n) называются левым и правым сингулярными

векторами. В форме S = svd(А) возвращает вектор сингулярных зна-

чений матрицы А, допустимы также полная [U,S,V] = svd(А) и эконо-

мичная [U,S,V] = svd(A,0), [U,S,V] = svd(A,'econ') формы обращения,

последняя выводит только min(m, n) столбцов матриц U, S, V;

rref(A) преобразование матрицы А к треугольному виду ме-

тодом исключения Гаусса. Правая часть матрицы R=rref([А eye(3)])

будет содержать обратную матрицу к А(3×3);

compan(Р) сопровождающая к полиному Р матрица Фробениуса

с характеристическим полиномом в первой строке;

jordan(A) преобразование матрицы А к модальной форме

Жордана с комплексными собственными значениями на главной диа-

гонали.

>> P=[1 2 3 4];

>> a=compan(P)

a =

-2 -3 -4

1 0 0

0 1 0

>> jordan(a)

ans =

-0.1747 + 1.5469i 0 0

0 -1.6506 0

0 0 -0.1747 - 1.5469i

Функции size() и length() позволяют определить размер матрицы

или вектора.

>> a=[1 2 3];

>> size(a)

ans =

1 3

>> length(a)

ans =

Функции fliplr() и flipud() позволяют отразить (повернуть) мат-

рицу или вектор относительно вертикали и горизонтали, функция