Бороденко В.А. Исследование систем управления в среде MATLAB

Подождите немного. Документ загружается.

121

RelTol: 1.0000e-008

Offset: 1.0000e-008

pzoptions

FreqUnits: 'rad/sec'

Заголовки полей отдельных свойств-структур позволяет полу-

чить команда get(объект, 'свойство'), например

>> P=timeoptions;

>> get(P,'Title') % Параметры заголовка графика

ans =

String: 'Time Response'

FontSize: 8

FontWeight: 'Normal'

FontAngle: 'Normal'

Color: [0 0 0]

Interpreter: 'tex'

>> get(P,'TickLabel') % Параметры оцифровки шкалы и легенды

ans =

FontSize: 8

FontWeight: 'Normal'

FontAngle: 'Normal'

Color: [0 0 0]

>> P.Title.String='Переходная характеристика';

>> P.TickLabel.FontSize=12;

>> step(sys,P) % Изменяем параметры графика

Свойство «наклон шрифта» FontAngle имеет варианты курсив

italic, норма normal, наклонный oblique, свойство «толщина шрифта»

FontWeight – тонкий light, норма normal, полужирный demi, жирный

bold.

Команда H=typeplot(…) возвращает идентификатор построен-

ного графика typeplot, используя который, можно получить параметры

графика командой getoptions и изменить их командой setoptions, руко-

водствуясь списком свойств конкретного графика.

>> H=stepplot(sys);

>> setoptions(H,'RiseTimeLimits',[0 1],'Normalize','on')

Заметим, что не всегда заявленные свойства реализуются – так,

хотя в команде nyquist(sys, P) показ кривой для отрицательных частот

был заблокирован и в контекстном меню Show-Negative Frequencies

флажок отсутствует, однако на графике отображены как основная

кривая, так и ее зеркальное отражение для отрицательных частот (ри-

сунок 2.6). Таким образом, надежнее пользоваться контекстным меню

графоанализатора LTI Viewer.

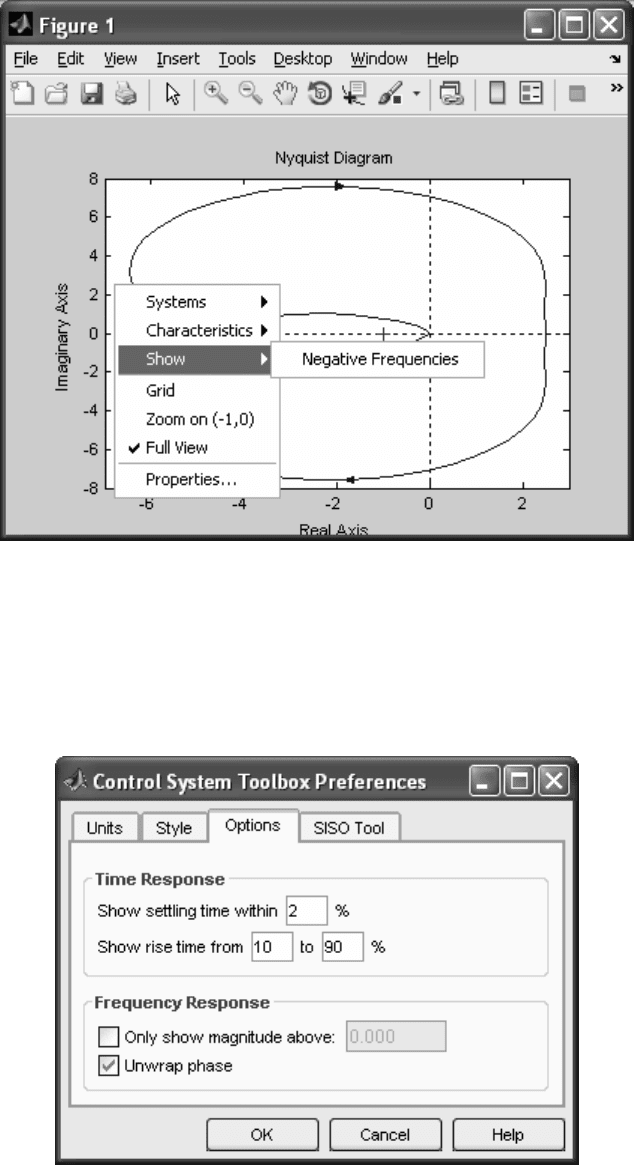
122

>> sys=tf(10,[1 2 3 4]);

>> P=nyquistoptions; P.ShowFullContour='off';

>> nyquistplot(sys,P)

Рисунок 2.6

Только в LTI Viewer, вызвав через меню File-Toolbox Preferences

окно Control System Toolbox Preferences (рисунок 2.7), можно задать

установки не для какого-то конкретного графика, а общие для всего

пакета.

Рисунок 2.7

123

Здесь на вкладке Options рекомендуется установить зону Δ для

контроля времени регулирования не 2, а 5 %, и убрать птичку в окне

Unwrap phase, что ограничит фазовые характеристики диапазоном

-180 ... +180 градусов. На вкладке инструмента SISO Tool можно за-

дать способ отображения регулятора Compensator Format (через по-

стоянные времени Time Constant, через частоты сопряжения Natural

Frequencies, через нули/полюса/коэффициент Zero/Pole/Gain) и показ

корней ПФ объекта, датчика на диаграмме Боде.

Это же окно вызывает команда ctrlpref.

Основной функцией для построения нестандартных двумерных

графиков является функция plot(), придерживающаяся стандартов,

описанных выше для графического анализатора, при задании цвета

Color, типа линии LineStyle и ее ширины LineWidth, вида маркеров

MarkerType и их размера MarkerSize. Для любого массива веществен-

ных данных при обращении plot(y), будет построен график с исполь-

зованием по оси абсцисс (горизонтальной) количества точек. Если же

Y является комплексной величиной, то ее действительные значения

откладываются по оси абсцисс, мнимые – по оси ординат.

При обращении plot(x,y), где x и y векторы одинаковой длины,

значения элементов x откладываются по оси абсцисс, значения эле-

ментов y – по оси ординат (вертикальной). При условии равенства

длины векторов-результатов в качестве аргументов могут быть ис-

пользованы функции, например, plot(t,cos(t)). Аргументами функции

могут быть обе матрицы, либо сочетания вектор-матрица, матрица-

вектор, от соотношения количества их строк и столбцов будет зави-

сеть число и вид выводимых в одном окне графиков. Так, команды

t=0:0.1:5; plot(t,[sin(t); cos(t)]) строят две зависимости одновременно.

Совмещение при построении в одном окне нескольких графиков

с независимым управлением цветом и типом линий обеспечивается

формой обращения plot(x1,y1,'s1',x2,y2,'s2'), где каждая тройка аргу-

ментов должна содержать данные для оси абсцисс Х, оси ординат Y, и

может содержать строковую переменную S с параметрами линии. При

обращении одинаковые данные для оси абсцисс должны все равно по-

вторяться в каждой тройке (двойке) аргументов plot(x,y1,x,y2,'k--') –

здесь откладываются одинаковые значения по оси х.

Помимо строковой переменной, установка дополнительных па-

раметров линии возможна и с использованием принципов объектно-

ориентированного программирования. Так, команда plot(x, y, 'line-

width', 2, 'color', [0.6 0 0]), использующая соответствующие свойства

линии как объекта, обеспечивает построение графика линией шири-

ной (LineWidth) 2 пункта темно-красного цвета (Color). Цвет задается

124

в стандарте RGB вектором [красный зеленый синий] с пределами

уровня по каждому оттенку 0.0-1.0, вычисленному по отношению

значения цвета в палитре RGB к максимальному значению 255. Кроме

того, для маркеров в виде геометрических фигур могут быть заданы

цвет ободка MarkerEdgeColor и заполнителя MarkerFaceColor.

Управление масштабом графика и видом осей координат произ-

водится функцией и оператором axis. Масштаб для текущего графиче-

ского окна задается в форме axis([x1,x2,y1,y2]) и может быть получен

в виде вектора v из четырех элементов командой v = axis. Режим ото-

бражения осей mode в команде axis mode выбирается из списка: auto –

устанавливается по умолчанию, пределы по осям выбираются так,

чтобы график не касался границ окна; tight – график точно вписывает-

ся в окно; equal – устанавливает одинаковый масштаб изображения по

обеим осям, что соответствует реальному виду графика; square – уста-

навливает одинаковый размер изображения по осям независимо от

масштаба; normal – отменяет действие двух предыдущих команд; off –

удаляет все вспомогательные построения, сохраняя только график; on

– отменяет действие предыдущей команды. Добавочные команды:

clf – очистка текущего графического окна во избежание наложе-

ния нового изображения на старое;

hold on/off – оставляет открытым текущее графическое окно (on)

для вывода в него следующих графических объектов или закрывает

его (off), оператор hold без дополнительного параметра действует как

переключатель, т.е. осуществляет переход в противоположный режим;

box on/off или просто box – переключатель показа рамки окна;

subplot(m,n,k) – выделяет несколько графических окон в виде

элементов матрицы размером m на n, отсчитывая номер окна k слева

направо, сверху вниз построчно. Например, subplot(2,2,3) объявляет

текущим левое окно снизу из четырех возможных;

title('txt'), xlabel('txt'), ylabel('txt') используют заданный текст в

качестве заголовка окна, оси Х, оси У. Функция text(x,y, 'txt') разме-

щает текст в графическом окне от точки с физическими координатами

xmin<x<xmax, ymin<y<ymax, функция text('txt') ждет для размещения

текста выбора позиции мышью и щелчка левой кнопкой, функция leg-

end() создает прямоугольник с поясняющими подписями. Все эти

функции и функции нанесения линий, стрелок на график доступны в

режиме редактирования фигуры из меню Insert или кнопкой Edit plot.

При проблемах с русскими шрифтами в Windows XP рекомендуется в ветви

реестра Hkey_Local_Machine\System\CurrentControlSet\Control\Nls\Codepage,

пользуясь командами выполнить-regedit, установить значения кодовых страниц

1250 = "c_1251.nls", 1252 = "c_1251.nls", либо в заголовках избегать использова-

ния русских символов «с» и «я».

125

Все возможности функции plot() имеются и у функций loglog(),

semilogx(), semilogy(), которые отличаются тем, что строят графики в

логарифмическом масштабе соответственно по обеим осям, по оси Х,

по оси У. Функция plotyy() строит график с обозначениями оси У как

слева, так и справа. Основные формы обращения: plotyy(x1,y1,x2,y2) –

пара х1, у1 для левой оси ординат, пара х2, у2 для правой; вызов в

форме plotyy(x1,y1,x2,y2,fun) уточняет способ построения графика,

например, plotyy(x1,y1,x2,y2,@loglog) или plotyy(x1,y1,x2,y2,'loglog'),

из списка plot, semilogx, semilogy, loglog. Если указаны две функции

plotyy(x1,y1,x2,y2,fun1,fun2), то fun1(x1,y1) строит график для левой

оси У, а fun2(x2,y2) предназначена для правой оси ординат.

К области специальной графики относятся функции:

polar(Phase, Mag) – построение в полярных координатах зависи-

мости модуля вектора Mag от его угла Phase (рад);

compass(U, V) – построение в полярных координатах векторной

диаграммы по проекциям U (ось абсцисс) и V (ось ординат). Каждый

вектор отображается стрелкой из начала координат, U и V могут быть

наборами данных для нескольких векторов;

contour() – построение линий равного уровня в пространстве

двух параметров по предварительно сформированной сетке;

fplot(f,[a,b]) – построение графика функции f в интервале (a, b).

Командой ezplot() осуществляется построение графика сим-

вольной функции, которая может быть задана непосредственно име-

нем ezplot(eq2,x1,x2), либо как строковая переменная ezplot('sin(x)').

Диапазон изменения переменной х может быть указан специально ez-

plot(f1,f2,[xmin,xmax]), либо оставлен на усмотрение программы

ezplot(f1,f2), тогда 0 < x < 2. Пределы изменения переменных х1 и х2

могут указываться без квадратных скобок, если это целые числа, либо

в квадратных скобках в ином случае; если они не указываются, про-

грамма использует значения по умолчанию. При исследовании двух

функций одной переменной f1(x) и f2(x) график использует первую из

них для организации изменения по оси Х, вторую – по оси У.

Для функции двух переменных f(x, y)=0 возможны обращения:

ezplot(f,[xmin,xmax,ymin,ymax]) при разных пределах изменения x и y;

ezplot(f,[a,b]) – при изменении обеих переменных в диапазоне от a до

b. В данном случае в описание функции не включают ноль и знак ра-

венства, так как программа их ставит автоматически, поэтому функ-

цию нужно приводить к соответствующему виду. Например, вместо

записи 'x^2+y^2=1' следует вводить 'x^2+y^2-1'. Первые по порядку

пределы указываются для переменной, встречающейся в описании

функции также первой, независимо от ее имени.

126

2.5 Программирование в MATLAB

Основные виды структур управления в MATLAB:

оператор if (elseif, else) … end проверки выполнения условий;

оператор switch (case если выполнено условие, otherwise в ином

случае) … end выбора исполняемого действия;

операторы цикла с известным for … end и неопределенным

while … end числом выполнений;

оператор parfor for-цикла для параллельных вычислений;

оператор continue продолжения цикла;

операторы блока try … catch ME … end с переводом действий по

неправильному результату пробных действий;

оператор break досрочного выхода из того блока for или while, в

котором он встречается;

оператор return выхода из тела функции.

Как только написан первый оператор структурного блока, вы-

полнение в прямом режиме приостанавливается до ввода оператора

конца блока end.

Цикл for повторяет действия заданное число раз, например, от 1

до m для i, от 1 до n для j

for i=1:m

for j=1:n

H(i,j)=1/(i+j);

end

при этом может быть указан шаг изменения for i=1:0.1:2, в том числе

отрицательный for i=1:-0.1:0. По умолчанию шаг равен 1, если усло-

вие цикла неосуществимо, цикл не выполняется ни разу. (Внимание!

Переменные i и j являются системными, они отведены под указание

мнимой единицы, поэтому следует внимательно относиться к их ис-

пользованию в прямом режиме во избежание переопределения).

Оператор Switch осуществляет выбор действия по условию, вы-

полняется только первый соответствующий случай. Выбор альтерна-

тивных путей алгоритма функционирования программируемой функ-

ции осуществляется операторами nargin и nargout, проверяющими со-

ответственно число входных и выходных переменных.

Функция pause останавливает выполнение программы с выво-

дом сообщения Paused: Press any key до нажатия пользователем любой

клавиши, вариант вызова pause(n) формирует задержку выполнения на

n секунд с автоматическим возобновлением операций, где n может

быть дробным числом с точностью 0.01. Для вывода сообщения об

127

ошибке или предупреждения используются функции error('текст') с

прекращением выполнения программы или warning('текст') с его про-

должением.

Функции num2str(Х) и int2str(Х) предназначены для перевода

вещественных и целых чисел Х в текстовые переменные, mat2str(Х)

преобразует числовую матрицу в строковую переменную, записанную

в формате MATLAB, обратное преобразование выполняет eval(str).

Дополнительно можно указать допустимое число значащих цифр N

при преобразовании и формат вывода, например, num2str(Х, N).

>> c=0.1234;

>> num2str(c)

ans =

0.1234

>> d=num2str(c,2)

d =

0.12

>> a=[1.123456 2 3;4 5 6;7 8 0.00009123];

>> a

a =

1.1235 2.0000 3.0000

4.0000 5.0000 6.0000

7.0000 8.0000 0.0001

>> b=mat2str(a,3)

b =

[1.12 2 3;4 5 6;7 8 9.12e-005]

Преобразование чисел позволяет выводить в одну строку дан-

ные разного типа, управлять форматом печати посредством функций

disp() и sprintf('%FORMAT', A, …).

>> disp({' число : ' d}) % каждый элемент в своей позиции

' число : ' '0.12'

>> disp([' число : ' d]) % все элементы подряд

число : 0.12

>> str=sprintf('%s%2.2f',' TimeSample: ',0.05); disp(str)

TimeSample: 0.05

Вызвав через меню File-New-Script редактор программ Editor,

можно записать текст фрагмента программы, а затем выполнить его

командой Debug-Save File and Run или Run для уже существующего.

Программирование в MATLAB удобно рассмотреть на примере

реализации алгебраических критериев Гурвица и Рауса в виде m-

файлов, позволяющих многократно использовать готовые функции.

Встроенных функций расчета критериев Рауса и Гурвица система

MATLAB не имеет. Для редактирования следует открыть редактор

128

(Editor) опцией меню File-New-Function.

Создадим пользовательскую функцию routh(), формирующую из

n коэффициентов полинома матрицу r размером n x m, где m = n/2 при

четном n и m = (n+1)/2 при нечетном n. Первые строки комментариев

после заголовка функции, начинающиеся символом %, обычно выво-

дятся на экран при запросе справки по функции, например, help routh.

Прекращается их вывод пустой строкой. Операторы в одной строке

разделяются символом «;», этот же символ в конце строки отменяет

немедленный вывод результата на экран.

Функция length() позволяет найти длину вектора (количество

коэффициентов полинома) n, которая и определит число строк в таб-

лице. Число столбцов m получим с помощью функции округления

round(). Применив функцию zeros(), создадим нулевую матрицу раз-

мером n на m. Символ двоеточия в MATLAB позволяет указывать це-

ликом строку, столбец матрицы, задавать числовой вектор его началь-

ным, конечным значением и шагом (если величина шага не указана,

по умолчанию она равна единице), либо крайними индексами элемен-

тов и шагом. Учитывая изложенное, запишем порядок вычисления

первой и второй строки таблицы.

n=length(p); m=round(n/2); r=zeros(n,m);

r(1,:)=p(1:2:n); r(2,1:fix(n/2))=p(2:2:n);

Функция fix(), отбрасывающая дробную часть числа, позволяет

соблюсти требования равенства размеров присваиваемого и читаемого

векторов для четного и нечетного n при формировании второй строки

таблицы Рауса.

Задача программирования расчета остальных элементов табли-

цы облегчается в MATLAB тем, что векторная форма задания измене-

ния переменной освобождает порой даже от необходимости записы-

вать сам цикл (например, как это сделано для переменной j).

for i=3:n

j=1:m;

r(i,j)=r(1-2,j+1)-r(i-1,j+1)*r(i-2,1)/r(i-1,1);

end

Цикл в MATLAB начинается словом for и заканчивается словом

end, аналогично формируется блок проверки условия if … end (без

слова then).

Осталось предусмотреть случай, когда в первом столбце оказы-

вается нулевой элемент r(i-1,1), на который делить нельзя. Рекоменду-

ется вместо нуля принять в этом случае очень маленькую положи-

тельную величину и продолжать вычисления. Воспользуемся для это-

129

го имеющейся в MATLAB константой realmin, которая и является ми-

нимально возможным действительным числом 2.2251е-308.

den=r(i-1,1);

if den==0

den=realmin;

end

Обратим внимание на то, что в MATLAB символ «=» соответст-

вует присваиванию, а равенство записывается двойным таким симво-

лом.

Результат, полученный при использовании созданной функции

routh() для оценки устойчивости полинома

P(x)=x

+ 2x

+ 3x

+ 4x

+ 5x

+ 6x + 7,

нельзя считать удовлетворительным.

>> p=[1 2 3 4 5 6 7]; routh(p)

ans =

1 3 5 7

2 4 6 0

1 2 7 0

0 -8 0 0

Inf 7 0 0

-8 0 0 0

NaN NaN NaN 0

Здесь Inf – обозначение бесконечности, эта величина может

иметь знак и не мешает анализу устойчивости, тогда как NaN (не чис-

ло, неопределенность), величина, получающаяся при операциях вида

умножения бесконечности на ноль, отношения двух нулей и т. п., не

способствует правильности анализа.

В силу этого введем вторую проверку – если элемент r(i-2,1) ра-

вен бесконечности Inf, что и ведет к появлению NaN, заменяем его на

очень большое число realmax, равное 1.7977е+308, сохраняя знак бес-

конечности

nom=r(i-2,1);

if abs(nom)==Inf

nom=realmax*sign(nom);

end

Повторим расчет для полинома p

>> routh(p)

ans =

1 3 5 7

130

2 4 6 0

1 2 7 0

0 -8 0 0

Inf 7 0 0

-8 0 0 0

7 0 0 0

Для большинства полиномов работа функции в таком виде бу-

дет удовлетворительной. Однако следует учесть и специальный слу-

чай, вызываемый наличием пар комплексных корней, одинаковых по

величине, но разных по знаку. Найдем корни такого полинома и при-

меним к нему созданную функцию

>> p=[1 3 8 18 37 75 50]; roots(p)

ans =

1.0000 + 2.0000i

1.0000 - 2.0000i

-1.0000 + 2.0000i

-1.0000 - 2.0000i

-2.0000

-1.0000

>> routh(p)

ans =

1 8 37 50

3 18 75 0

2 12 50 0

0 0 0 0

12 50 0 0

0 0 0 0

50 0 0 0

У полинома имеется два правых корня 1±j2, однако в первом

столбце полученной таблицы Рауса отсутствуют отрицательные эле-

менты, что приводит к неверному заключению. Признаком рассмат-

риваемого случая является строка, в которой все элементы нулевые

(четвертая сверху).

В таких случаях рекомендуют заменять нулевой ряд производ-

ной полинома, составленного из коэффициентов предшествующей

строки, по формулам

...)( ;)( ;)(

,,,,,, 3i31i2i21i1i11i

r3inrr1inrr1inr 



Дополним данные формулы условием, что количество значащих

коэффициентов в строке должно быть больше одного, это позволит

избежать ошибки при наличии нулевого коэффициента в последней

или предпоследней строке.