Бороденко В.А. Исследование систем управления в среде MATLAB

Подождите немного. Документ загружается.

161

ное обращение sysp=pade(sysd,ni,no,nio), где векторы ni, no и матрица

nio определяют порядок аппроксимации независимо для каждого вхо-

да (input), выхода (output) и проходной I/O задержки. При отсутствии

задержек на входе, выходе или проходных задержек нужно указывать

в пропускаемой позиции пустую матрицу [ ].

От системы с задержками, имеющую по два входа и выхода



























1s414

e419

1s910

e66

1s021

e918

1s716

e812

)(

перейдем к системе Н без экспоненциальных функций, задав первый

порядок аппроксимации Паде для задержек величиной 1 и 3 с, второй

порядок аппроксимации Паде для задержки 7 с.

>> H=pade(Hd,[ ],[ ],[1 1;2 1])

Указанная в списке аргументов Нd – это исходная система с за-

держками в экспоненциальной форме. Новая Н-система не содержит

задержек в явном виде, но, тем не менее, воспроизводит их, погреш-

ности воспроизведения зависят от порядка аппроксимации. Размер

системы увеличивается на порядок аппроксимации задержки рядом

Паде, так, при объекте первого порядка и аппроксимации второго по-

рядка задержки 7 с получается система третьего порядка

Transfer function from input "R" to output...

–12.8 s + 25.6

Xd: ---------------------

16.7 s^2 + 34.4 s + 2

6.6 s^2 – 5.657 s + 1.616

Xb: ---------------------------------------

10.9 s^3 + 10.34 s^2 + 3.527 s + 0.2449

Transfer function from input "S" to output...

18.9 s – 12.6

Xd: ----------------------

21 s^2 + 15 s + 0.6667

19.4 s – 12.93

Xb: --------------------------

14.4 s^2 + 10.6 s + 0.6667

При преобразовании TF или ZPK объектов в SS модель все мат-

рицы вычисляются с установкой задержки в нуль, а задержка указы-

162

вается отдельно, при этом ssdata() и dssdata() задержку не отображают.

>> s = tf('s'); G = exp(-2*s)*5/(s^2 + 3*s + 2);

>> gs=ss(G)

a =

x1 x2

x1 -3 -2

x2 1 0

b =

x1 2

x2 0

c =

x1 x2

y1 0 2.5

d =

y1 0

Output delays (listed by channel): 2

Модель в пространстве состояний может иметь не только вход-

ную Input Delay или выходную Output Delay, но и внутреннюю Internal

Delay задержки. Например, система

)),(()()(

)()()(













tutty

tutt

DCx



имеет задержку τ между входом и вектором состояний, задержку θ

между вектором состояний и выходом.

Внутренняя задержка Internal Delay образуется автоматически

при конкатенации подсистем с выходной и входной задержками, ох-

вате элемента с задержкой обратной связью, переводе TF и ZPK моде-

лей с задержкой в пространство состояний.

Например, результатом параллельного соединения двух блоков

w=ss(w1)+w2 с ПФ w1=5*exp(-3*s)/(s+1) и w2=1/(s+2) будет система

w=(s+(5*s+10)*exp(-3*s)+1)/(s+1)/(s+2) с задержкой, которую нельзя

отнести ни к входным, ни к выходным, ни к проходным. Такая систе-

ма может существовать только как SS модель с внутренней задерж-

кой.

Временные и частотные характеристики систем с внутренней

задержкой моделируются точнее, чем при использовании аппрокси-

163

мации Паде. Для специального описания подобных систем использу-

ется функция sys = delayss(a,b,c,d,delayterms), в которой структура de-

layterms формирует массив задержек и матриц коэффициентов при за-

держках дополнительно к обычным матрицам A, B, C, D





jjjj

tttt

))()(()()(



uBxABuAx





jjjj

ttttt ))()(()()()(



uDxCDuCxy

где τ

, j=1,..,n – сами задержки в секундах. Структура delayterms со-

держит поля a, b, c, d, delay, причем delayterms(j) определяет значения

, A

, B

, C

, D

. Нулевые матрицы A

, B

, C

, D

задаются как пустые [],

размеры матриц A

, B

, C

, D

и A, B, C, D соответствуют друг другу.

Опишем систему с задержками в пространстве состояний

)()5.0()( ),5.0(2)2.1()()( tutxtytutxtxtx

















Формируем сначала структуру, включающую массив задержек с

пустыми (нулевыми) матрицами коэффициентов при задержках

>> DelayT = struct('delay',{0.5;1.2},'a',[],'b',[],'c',[],'d',[]);

затем заполняем матрицы коэффициентов a, b, c, d перед элементами с

задержкой, еcли они не нулевые

>> DelayT(1).b = 2; DelayT(1).c = 1; % матрицы при τ = 0.5 с

>> DelayT(2).a = -1; % матрицы при τ = 1.2 с

>> sys = delayss(-1,0,0,1,DelayT) % вводим основные матрицы

Можно описывать и сразу матрицы совместно с задержками

>> DelayT(1) = struct('delay',0.5,'a',0,'b',2,'c',1,'d',0);

>> DelayT(2) = struct('delay',1.2,'a',-1,'b',0,'c',0,'d',0);

>> sys = delayss(-1,0,0,1,DelayT)

a =

x1 -2

b =

x1 2

c =

y1 1

164

d =

y1 1

(values computed with all internal delays set to zero)

Internal delays: 0.5 0.5 1.2

Continuous-time model.

Заметим, что внутренние задержки хранятся отдельно от матриц

A, B, C, D, поэтому по указанным матрицам будет построен процесс

без запаздывания. Функции pole, zero, ssdata, get возвращают значения

полюсов, нулей, системных матриц, рассчитанные без имеющейся за-

держки с использованием аппроксимации Паде нулевого порядка. К

командам, не поддерживающим внутренние задержки, относятся

norm, isstable, initial, initialplot, balreal, balred, modred, rlocus, lqg, lqry,

kalman, lqgreg, lqgtrack, lqi и augstate, с меньшей точностью работают

функции margin и allmargin. Кроме того, для указанных систем не

производится преобразование в ZPK и TF модели, не поддерживается

работа с SISO Design Tool.

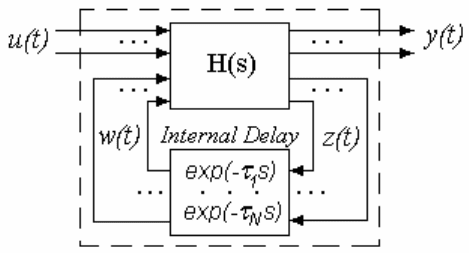
MIMO-модели с внутренней задержкой строятся в специальном

формате из двух частей – обычной системы в пространстве состояний

H(s), снабженной дополнительными выводами, и набора внутренних

задержек, связывающих эти выводы (рисунок 3.5).

Рисунок 3.5

Число задержек равно числу пар выход/вход дополнительных

выводов w, z и ограничено порядком системы, уравнения состояния

модели имеют расширенный вид.

wBuBAxxE





wDuDxCy



wDuDxCz



)()(

tztw





165

MATLAB переходит к такому представлению MIMO системы

автоматически, не требуя участия пользователя, однако можно из-

влечь модель H(s) и значения матриц А, В1 ... В2, C1 ... C2, D11 ... D22

функцией getDelayModel() или изменить некоторые величины функ-

цией setDelayModel(). Нельзя изменить число внутренних задержек,

так как оно уже заложено в структуре модели, например, в модели g

одна внутренняя задержка, но можно изменить ее величину.

>> s=tf('s');

>> p = 5*exp(-3.4*s)/(s+1);

>> c = 0.1 * (1 + 1/(5*s));

>> g = feedback(ss(p*c),1);

>> [H,tau] = getDelayModel(g,'lft')

a =

x1 x2

x1 -1 0

x2 1 0

b =

? w1

x1 1 -1

x2 0 0

c =

x1 x2

? 0 0

z1 0.5 0.1

d =

? w1

? 0 1

z1 0 0

Continuous-time model.

tau =

3.4000

За счет дополнительных выводов w1 и z1 для задержки 3.4 с

объект H имеет два входа и два выхода, хотя система g в целом имеет

по одному входу и выходу. Функции getDelayModel и setDelayModel

(обязательно с прописными M и D в имени, в нарушение заявленного

авторами MATLAB правила, что имена функций пишутся только

строчными буквами) используются в формах:

[H,tau] = getDelayModel(sys,'lft') – система целиком;

[a,b1,b2,c1,c2,d11,d12,d21,d22,e,tau] = getDelayModel(sys,'mat');

sys = setDelayModel(a,b1,b2,c1,c2,d11,d12,d21,d22,tau) – без мат-

166

рицы Е, т. е. только для нормированных систем;

sys = setDelayModel(H,tau), где Н – специальным образом по-

строенная система H = ss(a,[b1 b2],[c1;c2],[d11 d12;d21 d22]).

Для систем без внутренней задержки часть выведенных коман-

дой getDelayModel матриц и вектор задержек будут пустыми и вид

модели H не будет отличаться от обычного представления.

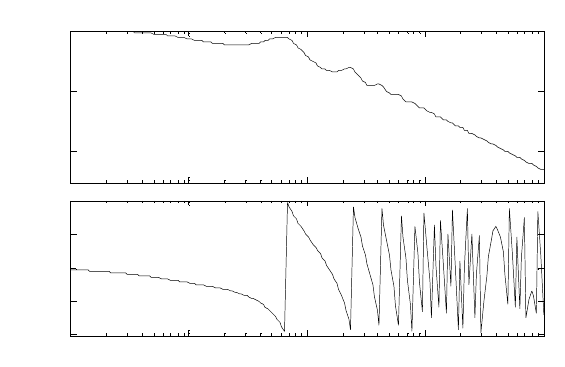
Поведение системы с внутренней задержкой характеризуется

осцилляцией коэффициента усиления (АЧХ) и многократными прово-

ротами вектора W(jω) относительно начала координат (рисунок 3.6).

-40

-20

Magnitude (dB)

-2

-1

-180

-90

180

Phase (deg)

Bode Diagram

Рисунок 3.6

3.4 Преобразование форм модели

В процессе обучения приходится неоднократно вычислять раз-

личные специальные матрицы и преобразовывать формы описания

системы.

Сопровождающую матрицу (матрицу А в инверсной канониче-

ской форме описания системы) можно получить по характеристиче-

скому полиному Р функцией compan(P). Характеристическая матрица

вычисляется в символической записи, характеристический полином

является ее определителем.

>> a=[0 1 0;0 0 1;-4 -3 -2]; % задаем матрицу А третьего порядка

>> syms s % определяем символьную переменную s

>> sa=s*eye(3)-a % вычисляем характеристическую матрицу

sa =

[ s, -1, 0]

[ 0, s, -1]

[ 4, 3, s+2]

>> det(sa) % определитель характеристической матрицы

167

ans =

s^3+2*s^2+3*s+4

Системную матрицу или резольвенту Ф(s) можно получить от-

дельно, либо как обратную матрицу к известной характеристической

>> inv(sa) % вычисляем резольвенту по найденной выше матрице sa

ans =

[(s^2+2*s+3)/(s^3+2*s^2+3*s+4), (s+2)/(s^3+2*s^2+3*s+4), 1/(s^3+2*s^2+3*s+4)]

[-4/(s^3+2*s^2+3*s+4), s*(s+2)/(s^3+2*s^2+3*s+4), s/(s^3+2*s^2+3*s+4)]

[-4*s/(s^3+2*s^2+3*s+4), -(3*s+4)/(s^3+2*s^2+3*s+4), s^2/(s^3+2*s^2+3*s+4)]

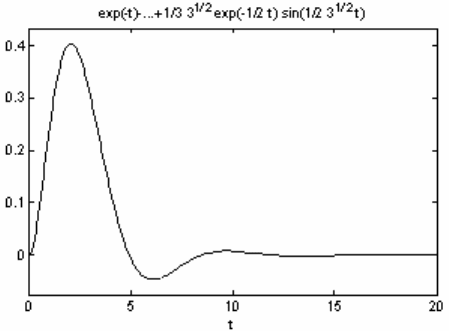
Для некоторых частных передаточных функций при определен-

ных сочетаниях полюсов можно сразу получить оригинал с помощью

обратного преобразования Лапласа и построить график (рисунок 3.7)

>> syms s t % объявляем символьные переменные

>> w=1/(s^3+2*s^2+2*s+1); % описываем изображение W(s)

>> y=ilaplace(w) % обратное преобразование Лапласа от w по t

y =

exp(-t)-exp(-1/2*t)*cos(1/2*3^(1/2)*t)+1/3*3^(1/2)*exp(-1/2*t)*sin(1/2*3^(1/2)*t)

>> ezplot(y,0,20) % строим график y(t) в диапазоне 0-20 с

Рисунок 3.7

Помимо обратного преобразования Лапласа, фундаментальную

матрицу можно получить как матричную экспоненту от At, например

>> syms t; A=[0 1;-2 -3];

>> expm(A*t)

ans =

[ -exp(-2*t)+2*exp(-t), exp(-t)-exp(-2*t)]

[ -2*exp(-t)+2*exp(-2*t), 2*exp(-2*t)-exp(-t)]

Во многих случаях запись фундаментальной матрицы сущест-

венно упрощается, если матрица А представлена в блочной модальной

168

форме Жордана

>> A=[-1 0 0;0 -1 2;0 -2 -1];

>> syms t

>> expm(A*t)

ans =

[ exp(-t), 0, 0]

[ 0, exp(-t)*cos(2*t), exp(-t)*sin(2*t)]

[ 0, -exp(-t)*sin(2*t), exp(-t)*cos(2*t)]

При записи в диагональных клетках матрицы Жордана ком-

плексных собственных значений получающаяся в фундаментальной

матрице мнимая составляющая переходного процесса должна быть

смещена в соседнюю клетку блока.

Матрицы управляемости (controllability) Q и наблюдаемости

(observability) N формируются в MATLAB командами ctrb() и obsv(),

причем последняя иначе, чем принято в СНГ, без транспонирования

матриц А и с (в соответствии со свойством матриц А

= (сА)

Затем с помощью функции rank() вычисляется ранг матриц. До-

пустимы формы ctrb(sys) и ctrb(A, b), obsv(sys) и obsv(A, c).

Ранг матрицы управляемости объекта регулирования g равен

порядку объекта n = 2, следовательно, он полностью управляем.

>> ctrb(g)

ans =

1.0000 -0.5000

0 1.0000

>> rank(ans)

ans =

Ранг матрицы наблюдаемости объекта регулирования g равен

порядку объекта n = 2, следовательно, он полностью наблюдаем.

>> obsv(g)

ans =

0 0.2500

0.2500 0

>> rank(ans)

ans =

В пространстве состояний возможно бесчисленное множество

описаний одной и той же системы, однако удобнее использовать не-

сколько стандартных форм. Рассмотрим применение штатных функ-

ций MATLAB на примере системы с передаточной функцией

169

W(s)=(s^2 + 3 s + 2)/(s^3 + 5 s^2 + 11 s + 15), имеющей нули -1, -2,

полюса -3, -1±j2 и коэффициент усиления 1.

Функция ss() используется для построения SS модели по матри-

цам A, B, C, D или модели системы, описанной в иной форме (кроме

FRD модели). Она приводит TF модель к так называемой модифици-

рованной (сбалансированной) канонической форме с примерно рав-

ными нормами матрицы А по строке и столбцу.

MATLAB может выполнять балансировку системных матриц,

необходимую в случае, если образующие эти матрицы элементы от-

личаются друг от друга на несколько порядков, что увеличивает по-

грешность компьютерных вычислений. Операция балансировки заме-

няет фактические системные матрицы более пригодными для чис-

ленных расчетов, уравнивая различные нормы матрицы А. Норма

матрицы по строкам определяется как наибольшая из сумм абсолют-

ных значений чисел каждой строки, а норма матрицы по столбцам оп-

ределяется как наибольшая из сумм абсолютных значений чисел каж-

дого столбца. Команда [sysb, T] = ssbal(sys) возвращает вместо исход-

ной системы сбалансированную sysb с примерно равным нормами по

строке и столбцу, а также матрицу преобразования подобия Т, позво-

ляющую при необходимости рассчитать фактические фазовые коор-

динаты системы.

Функция tf2ss() преобразует TF модель в псевдоканоническую

инверсную управляемую форму SS модели с коэффициентами харак-

теристического полинома в верхней строке матрицы А – переменные

назначаются со входа системы, а не с выхода, как в методе фазовых

переменных. В соответствующем порядке записываются и элементы

матриц В и С.

>> [a,b,c,d]=tf2ss(num,den)

a =

-5 -11 -15

1 0 0

0 1 0

b =

c =

1 3 2

d =

Обратное преобразование [num, den]=ss2tf(a, b, c, d, iu) требует

указания индекса входа iu, если входов у системы несколько, и выво-

170

дит матрицу num с числом строк, равным числу выходов системы.

Преобразование ZPK модели в управляемую SS модель с произ-

вольно образованной матрицей А производится функцией zp2ss(z,p,k),

где число столбцов матрицы z и вектора k должно быть равно количе-

ству выходов системы.

>> z=[-1 -2];p=[-3,-1+2i,-1-2i];k=1; [a,b,c,d]=zp2ss(z,p,k)

a =

-3.0000 0 0

1.0000 -2.0000 -2.2361

0 2.2361 0

b =

c =

1.0000 1.0000 -1.3416

d =

Обратное преобразование [z, p, k]=ss2tf(a, b, c, d, iu) требует ука-

зания индекса входа iu, если входов у системы несколько, и выводит

матрицу нулей Z с числом столбцов, равным числу выходов системы.

Каноническая модальная форма характеризуется тем, что в мат-

рице А собственные значения расположены по диагонали, причем ис-

пользуются лишь вещественные числа, поэтому каждая пара ком-

плексных корней выводится в виде блока, у которого действительные

части находятся на главной диагонали, а мнимые – справа (положи-

тельная) и слева (отрицательная) от нее.

>> sys=canon(w,'modal')

a =

x1 x2 x3

x1 -3 0 0

x2 0 -1 2

x3 0 -2 -1

b =

x1 3.881

x2 3.69

x3 1.23

c =

x1 x2 x3

y1 0.06442 0.1626 0.122

d =

y1 0