Graef M. Introduction to conventional transmission electron microscopy

Подождите немного. Документ загружается.

178 The transmission electron microscope

3.6.2 Quadrupole elements

A quadrupole lens is a lens with two orthogonal planes of symmetry, and two

additional planes of anti-symmetry oriented at 45

◦

with respect to the symmetry

planes (Fig. 3.20a). In the absence of currents in the ﬁeld region, the magnetic

induction inside such a lens can be derived from the scalar magnetic potential

ω(x, y, z). One can show [Szi88] that this potential is to a good approximation

described by

ω(x, y, z) = F(z)xy,

where F(z) is a function which describes the axial variation of the ﬂux density.

Equipotential contours for this potential are shown in Fig.3.20(a). The magnetic

ﬁeld components are determined from the gradient of the scalar potential:

=−µF(z)y

=−µF(z)x

=−µF



(z)xy.

Figure 3.20(b) shows such a magnetic ﬁeld conﬁguration in between the pole

pieces. Note that if F(z) is constant inside the quadrupole lens, then there is no

axial component to the ﬁeld and the ﬁeld components lie entirely in a plane per-

pendicular to the optical axis. For electrons traveling nearly parallel to the optical

axis the resulting Lorentz force will also be normal to the axis. Because of the cross

product nature of the Lorentz force we ﬁnd that the force vectors are tangent to

the equipotential lines for an electron traveling parallel to the optical axis. Such a

ﬁeld geometry may hence be used to change the shape of the electron beam. Con-

versely, a beam affected by astigmatism can be restored to a circular shape. The

main use of quadrupole lenses in the transmission electron microscope is therefore

to correct astigmatism in the beam. This is typically done at two locations: the ﬁrst

set of quadrupole lenses is located between the last condensor lens and the beam

deﬂectors. A photograph of such a correction coil is shown in Fig. 3.20(c). This

correction coil is actually a pair of quadrupoles oriented at 45

◦

with respect to each

other. This permits adjustments of the beam shape in two orthogonal directions.

The second set of astigmatism correctors is located immediately below the objective

lens lower pole piece, and is typically much smaller than the condensor stigmator –

a photograph is shown in Fig. 3.20(d). These correction coils are among the most

important components of a modern electron microscope. We will see in Chapter

10 that without astigmatism correction coils, the resolution of a TEM would be

around 1 nm, not good enough for observations at the length scale of interatomic

distances.

3.7 Basic electron optics: electron guns 179

3.7 Basic electron optics: electron guns

3.7.1 Introduction

In this section, we will discuss one of the most essential components of a TEM: the

electron gun. The main purpose of the electron gun is to provide a steady stream

of electrons with a constant kinetic energy, i.e. a monochromatic electron beam.

Ideally, the electrons should appear to emanate from a single point on the ﬁlament

surface, so that the gun can be described as a point source. In addition, since we

have seen in the preceding sections that several lens aberrations depend on the

angle between the trajectory and the optical axis, the electrons should travel close

to the optical axis, at very small angles to the axis. Finally, after passing through

the entire column (including the sample) there must be sufﬁcient electrons left over

to form an image on the detector (screen, micrograph, etc.) to acquire the data in

a reasonable amount of time (exposure time). This means that the image current

density, the number of electrons per second that hit a unit area of the detector, must

be reasonably high.

These qualitative statements can be cast into more precise mathematical terms,

and the design of electron guns is a highly specialized ﬁeld, similar to the de-

sign of magnetic lens elements. The basic design process goes as follows: for a

given geometry of the ﬁlament and all potential surfaces around the tip, the elec-

tric equipotential surfaces are computed, typically by ﬁnite element analysis. The

trajectory equation is solved for a large number of trajectory starting points, and

the properties of the assembly are computed, including aberrations. The design

parameters are then varied until the desired functionality is obtained.

We will discuss the various types of electron guns in the following subsections.

First, we will describe the physics behind the process of electron emission.

3.7.2 Electron emission

In this section, we will closely follow a paper by Fransen et al. [FCRT

99] and

Chapter 44 in [HK89b]. For simplicity we will represent the surface of the ﬁlament

tip as a ﬂat surface of unspeciﬁed lateral dimensions. The z-axis is taken to be normal

to the surface. At absolute zero, the energy distribution of the electrons inside the

metal is rather simple: all energy levels up to a maximum energy are occupied.

This maximum energy is known as the Fermi energy E

. When the temperature

is increased, some electrons will gain sufﬁcient thermal energy to occupy higher

energy states. The distribution of occupied states is described by the Fermi–Dirac

distribution:

(

E, T

)

≡

1 + e

[

E−(E

−V

)

]

, (3.46)

180 The transmission electron microscope

Energy (eV)

-1

10246

z (nm)f (E, T)

0 K

1800 K

image charge

applied field (W - eFz)

F=0.5 V/nm

F=1

F=2

F=4

∆W

(

W -

16πε

)

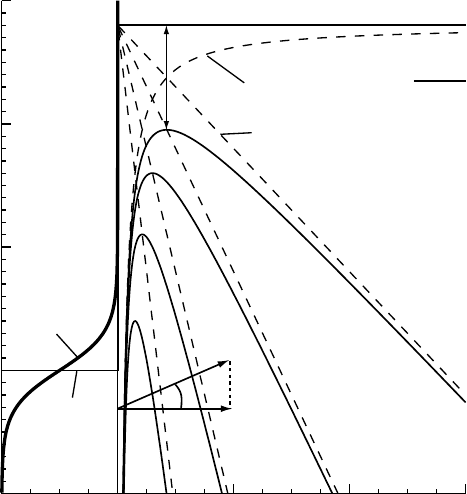
Fig. 3.21. Schematic illustration of the Fermi–Dirac function at 0 and 1800 K (left-hand

side). The barrier potential V (z) (in eV) is shown as a solid line for applied ﬁeld strengths

of F = 0.5, 1, 2, and 4 V nm

−1

, and a work function W = 2.8 eV. The components of V (z)

are shown as dashed lines. (This ﬁgure is based on Fig. 2 in [FCRT

99].)

where k

is the Boltzmann constant (8.618 16 × 10

−5

eV K

−1

), and V

is a constant

used to adjust the energy origin. As the temperature increases, the Fermi–Dirac func-

tion develops a high-energy tail, as shown on the left in Fig. 3.21 for a temperature

of T = 1800 K and V

= E

The energy needed for an electron to escape the metal is given by the work

function, W . The work function is equal to the difference between the vacuum

energy level and the Fermi level, and depends on both the atom type and the crystal

plane forming the metal surface. For pure tungsten the work function is 4.5 eV, while

for ZrO-coated (001) tungsten, W is reduced to 2.8 eV. If the ﬁlament temperature

is sufﬁciently high so that energy states above the vacuum level are occupied,

then electrons will be emitted into the vacuum. This process is known as thermal

emission. If an electric ﬁeld is applied between the metal surface and an external

electrode, then the vacuum level becomes a function of the distance to the surface

and is represented by the barrier potential V (z). It is customary in the electron

emission literature to represent this electric ﬁeld by the symbol F instead of E,

since E is already taken to represent the microscope acceleration voltage.

3.7 Basic electron optics: electron guns 181

The energy V (z) depends on the workfunction W , the applied ﬁeld F, and also

on the Coulomb interaction between the emitted electron and its mirror image in

the metal surface. An explicit expression is given by

V (z) = W − eFz −

16π

(z > 0); (3.47)

= W − Fz −

0.359 95

[

]

(with F in V nm

−1

, z in nm).

The zero of potential energy in this case is taken at the Fermi level. Figure 3.21

shows the function V (z) for several ﬁeld strengths F and a work function of 2.8eV

[FCRT

99]. The dashed lines indicate the Coulomb term and the electric ﬁeld term.

It is clear that with increased applied ﬁeld strength the barrier energy becomes lower

by an amount W . This lowering is known as the Schottky effect. It is left to the

reader to show that

W =

4π

= 1.1998

√

[

]

(with F in V nm

−1

). (3.48)

The main question to be answered is then: what is the emitted current density

in the z-direction at a given temperature and applied ﬁeld? While the general solu-

tion to this problem is still unknown, there are several special cases for which an

approximate analytical solution is possible. For an electron that has left the metal

with momentum p we have a total energy of

E =

p · p

+ V (z).

This energy can be decomposed into components normal and tangential to the

surface. We deﬁne (following [HK89a])

≡

+ V (z); U

≡



+ p



Not every electron with the correct energy will actually escape from the metal. A

fraction of the electrons will be reﬂected from the surface and return to the bulk of

the metal. The fraction of electrons that is actually emitted is described by D(U

the transmission coefﬁcient.

Next, we consider an elementary volume in momentum space, d

p.Ifweuse

cylindrical coordinates, as shown in Fig. 3.21, then we can rewrite this volume

182 The transmission electron microscope

element as

p = sin θ p

dp dθ dφ,

= sin θ p( p d p)dθ dφ,

= sin θ



2m(E − V (z))(m dE)dθ dφ,

where we have used p

= 2m[E − V (z)] and p dp =

d(p

) = m d( p

/2m) =

m dE. The total number N (p) of electrons with momentum between p and p + dp

that have enough energy to escape the metal is given by the product of the number of

quantum states per elementary volume in momentum space (2/ h

), the probability

that the electron will have the correct energy (the Fermi–Dirac function), and the

probability that the electron will not be reﬂected (D(U

)), or

N (p) =

D(U

)

1 + e

(E −E

)/k

The current density element d

j is then given by

j = e

N (p)d

p f (E, T )D(U

p. (3.49)

Since we are mostly interested in the current density component along the

z-direction we can use p

√

2m[E − V (z)] cos θ to obtain [FCRT

99]:

2me

[E − V (z)]

1 + e

(E −E

)/k

D(U

) sin 2θ dE dθ dφ. (3.50)

For a given model for D(U

) and V (z), this equation can be integrated over all

angles (0 <φ<2π ;0<θ <π/2), and over all appropriate energies to obtain the

total emitted current density. We will now consider some special cases for which

these integrations can be carried out analytically.

3.7.2.1 Thermionic emission

In the case of thermionic emission, there is no external applied ﬁeld and the origin

of the energy scale can conveniently be chosen to coincide with the vacuum level.

The potential barrier in the absence of a ﬁeld vanishes outside the crystal, and

the transmission coefﬁcient D(U

) = 1 for positive U

. At high temperature, the

Fermi–Dirac function can be simpliﬁed by dropping the 1 in the denominator and

3.7 Basic electron optics: electron guns 183

we ﬁnd for the current density (3.50):

2me

2π

dφ

π/2

sin 2θ dθ

+∞

−(E +W )/k

dE,

= AT

−W/k

≡ j

, (3.51)

with

A =

4πmek

= 1.201 75 × 10

This equation is known as the Richardson–Dushman equation, and can be used to

determine the work function W from measurements of the current density j

(T )

at different temperatures. For a tungsten ﬁlament with W = 4.5 eV, operated at

T = 2700 K, we have j

≈ 3.5Acm

−2

. A lanthanum-hexaboride ﬁlament (LaB

)

with a work function of W = 2.7 eV is typically operated between T = 1800 K

( j

= 10.7Acm

−2

) and T = 1900 K ( j

= 29.9Acm

−2

3.7.2.2 Schottky emission

We have seen previously that in the presence of an electric ﬁeld F of the order of

1Vnm

−1

the barrier energy is reduced by an amount W . The emission current

density of a Schottky emitter is then given by equation (3.51) with W replaced by

W − W ,or

= e

W/k

. (3.52)

The emission current is hence enhanced with respect to the thermionic emission

current. For a ZrO-coated tungsten single crystal ﬁlament with a work function of

W = 2.8 eV and an applied ﬁeld of 1 V nm

−1

(W = 1.2 eV), the current density is

= 1.3 × 10

Acm

−2

, about three orders of magnitude larger than for thermionic

emission.

Equation (3.52) is valid as long as tunneling through the potential barrier can

be ignored. If the applied ﬁeld is sufﬁciently strong, so that the potential barrier

becomes narrow (Fig. 3.21), then the transmission coefﬁcient D(U

) must be com-

puted explicitly. This is beyond the scope of this textbook and we refer to [FCRT

99]

for an explicit derivation of the so-called extended Schottky emission.

3.7.2.3 Thermal ﬁeld emission

In thermal ﬁeld emission the temperature of the ﬁlament is kept low (room tem-

perature) so that the high-energy tail of the Fermi–Dirac function nearly vanishes.

Electrons can only escape from near the Fermi level by tunneling through the nar-

row potential barrier, as shown in Fig. 3.21 for F = 4Vnm

−1

. The applied ﬁeld

184 The transmission electron microscope

is typically several volts per nanometer and the current density computation be-

comes rather lengthy; we refer to Fransen et al. [FCRT

99] for a brief description

and Kasper [Kas82] for a detailed account. The current density for thermal ﬁeld

emission is given by

4πme

−bW/d

π p

sin π p

. (3.53)

The factor d is a function of the applied ﬁeld and the work function (see [Kas82]):

d =

ehF

4πt(W/W )

√

2mW

9.7598 × 10

−2

t(W/W )

√

[eV] (F inVnm

−1

, W in eV),

with

t(y) = 1 + 0.1107y

1.33

b ≈ 0.6, and p = k

T/d. Equation (3.53) at T = 0 K is known as the Fowler–

Nordheim equation. For non-zero temperatures the equation is only accurate for

p < 0.7. Comparison with the Richardson–Dushman equation shows that d takes

on the role of k

T . For a tungsten ﬁeld emission tip operated at room temperature

(T = 300 K) and an applied ﬁeld of 7 V nm

−1

,wehaved = 0.3eV, p = 0.085,

and j

= 1.9 × 10

Acm

−2

3.7.2.4 Beam brightness

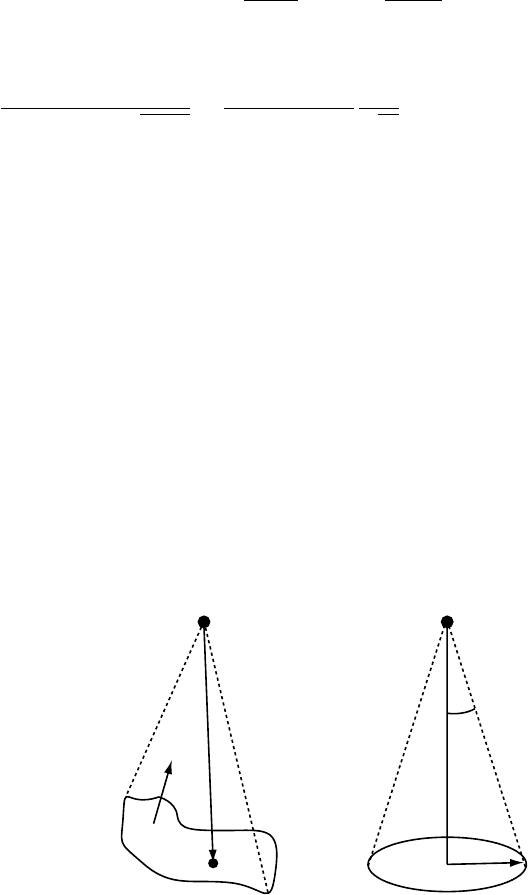
Let us assume that all electrons emanate from a circular region of radius r on the

tip of a ﬁlament. An observer at P, a distance q from the ﬁlament (Fig. 3.22b), will

then “see” an electron source with a surface area of πr

. The size of this source is

typically expressed as a solid angle rather than a surface area, since the apparent

(a) (b)

Fig. 3.22. Deﬁnition of the solid angle and the aperture semi-angle θ; (a) general case and

(b) for a cone.

3.7 Basic electron optics: electron guns 185

surface area depends on the distance q. Solid angle is deﬁned as the area subtended

by a surface S when looking at that surface from a reference point, divided by the

square of the distance to that surface,or

(S) =

r · n

with n the outward normal to the surface (Fig. 3.22a). For a sphere, the solid angle,

when looking from the center of the sphere, is equal to

 =

2π

sin θ dθ dφ = 4π.

The unit of solid angle is the steradian. The solid angle subtended by the base of a

cone with base radius r when viewed from the top is

 =

πr

= πθ

(see Fig. 3.22b) with q = r/θ the height of the cone.

The total current density j passing through the point P is proportional to the

solid angle subtended by the source at the point P, and the proportionality factor

β is known as the beam brightness:

β =

πθ

. (3.54)

Brightness is measured in amperes per unit area per steradian. If we represent the

current density j by the current I divided by the area A, then we can determine

how a magnetic lens affects the beam brightness. A magnetic lens with lateral

magniﬁcation M reduces the current density I /A to I /M

; the angular aperture

θ is increased by the angular magniﬁcation M

by a factor M

= 1/M

, so that the

total brightness remains unchanged. Brightness is hence a property of an electron

beam and is left unchanged by (aberration-free) magnetic lenses.

From the deﬁnition of brightness we ﬁnd that a higher current density will in-

crease the brightness; in other words, if we can get more electrons to emanate

from the ﬁlament emission area with a momentum inside the cone centered at P,

then the current density and hence the brightness would increase. In Section 3.7.2

we have seen that the energy of the emitted electron could be separated into two

components U

(corresponding to the momentum p

and the barrier potential) and

(corresponding to the momentum components p

and p

). It is then easy to

see that a rapid decrease of current density with increasing tangential momentum

components (and therefore with U

) will produce a higher brightness. The (axial)

186 The transmission electron microscope

brightness can hence be deﬁned as [FCRT

99, SM84]:

β ≡





d j



, (3.55)

with

 the relativistic acceleration potential introduced in Chapter 2. We can com-

pute the brightness for the various emission mechanisms discussed in the previous

section. The resulting brightnesses are given by

 j

πk

(thermionic emission); (3.56)

 j

πk

(Schottky emission); (3.57)

 j

πd

(thermal ﬁeld emission). (3.58)

The ION routine

emission.pro on the w

ebsite

can be used to display the barrier

potential V (z) and various quantities (current density, brightness, work function

reduction, etc.) for all three emission mechanisms described in this section. The

drawings produced by this routine are similar to that shown in Fig. 3.21.

Using the gun brightness we can compute the current density at any point along

the optical axis of the microscope, using equation (3.54). The current density in the

illumination spot after an aperture of diameter r, at a distance D from the aperture

plane, is given by

= πβ

)

For a tungsten hair-pin ﬁlament with β = 5 × 10

Acm

−2

−1

[Spe88] the current

density for a 400

µm diameter condensor aperture (r = 0.2 mm) is then approxi-

mately 1 A cm

−2

, using an approximate value for D = 250 mm, measured directly

on the cross-section of the microscope column discussed earlier in this chapter. If a

smaller condensor aperture is used, the current density goes down but the brightness

remains constant. The image current density at the phosphor screen for a magniﬁca-

tion of M = 500 000 is then 4 × 10

−12

Acm

−2

, i.e. current densities at the viewing

screen are of the order of a few pA cm

−2

. This determines the exposure time for

electron micrographs, when it is combined with the sensitivity of the emulsion (see

Section 3.11 on electron detectors). The maximum brightness for a given electron

gun is proportional to the acceleration potential and increases exponentially with

temperature; the lifetime of a ﬁlament decreases with increased temperature, so

there is an optimum operating temperature for the ﬁlament.

3.7 Basic electron optics: electron guns 187

Table 3.2. Approximate parameters for different electron guns

(sources: [Spe88, Rei93, WC96, FCRT

99]).

Thermionic emission Field emission

Tungsten LaB

Schottky Field emission

Work function [eV] 4.5 2.7 2.8 4.5

Operating temperature [K] 2700 1700 1800 300

Current density [A cm

−2

] 1–3 25–100 10

–10

Virtual source diameter [nm] 50 000 10 000 10–15 3–5

Brightness [A cm

−2

−1

]10

–10

Energy spread [eV] 1–3 0.5–2 0.3–1.0 0.2–0.3

Required gun vacuum [Pa] 10

−3

−5

−7

−8

Lifetime [h] 25–100 500–1000 >1000 >1000

Cost [U.S.$] 10–100 400–1200 1500–3500

1500–3500

Does not include installation costs.

3.7.3 Electron guns

In the previous section, we have described how many electrons are emitted from the

ﬁlament tip for a given work function, temperature, and applied ﬁeld. The shape of

the ﬁlament tip and the geometry of the applied ﬁeld did not enter the discussion at

any point. In reality, the geometry becomes very important because it determines

the trajectory of the electron once it has been emitted from the tip. Solving the

trajectory equations for a given gun geometry is far beyond the scope of this book

and we refer the interested reader to Chapters 43–50 in [HK89b] and references

therein.

In this section, we will describe the structure of the electron gun. Several differ-

ent gun types are available based on thermionic emission, (cold) ﬁeld emission, or

Schottky ﬁeld emission. Table 3.2 shows some of the relevant parameters for the

different electron guns. Descriptions of measurement techniques for gun charac-

teristics can be found in [Spe88, Section 7.2] and [WC96, Section 5.5].

3.7.3.1 Thermionic electron guns

Figure 3.23(a) shows a schematic drawing of the components of a thermionic

electron gun, also known as a triode gun, along with a photograph of the cross-

section of the gun of a JEOL 120CX TEM (Fig. 3.23b). The gun consists of three

basic components: the ﬁlament (F), the grid or Wehnelt cap, and the anode. The

ﬁlament is typically a hairpin-shaped tungsten wire or a pointed tungsten wire. In

the latter case the pointed wire is spot-welded to a tungsten support wire. A voltage

V produces a resistive heating current I

through the ﬁlament wire. Tungsten