Хейденрайх Р. Основы просвечивающей электронной микроскопии
Подождите немного. Документ загружается.


422
ПРИЛОЖЕНИЕIII
Фиг.
177 .
.индексы
ПЛОСКостей
в
гексагоналЬНЫХ
кристаллах.
описании
ЭКвивалентным
плоскостям
соответствуют
разные
индек
сы,
и
поэтому
для
гексагональных
кристаллов
часто
исполь
зуется
система
Миллера
-
Бравэ.
Индексы
Миллера
-
Бравэ
записываются
в
:виде
(h1!!l),
где
i =
-(h
+ k).
Плоскость
Призмы
(100)
записываетСЯ
(1010)
и
подобная
плоскость
(110) - (1100).
Базисная
плоскость
- (0001).
МеЖПЛОСКОСТI!ые
расстояния
для
Плоскостей
с
индексами
(hkl)
равны:
.
гексагональная
система
d -
(4
h
2
+hk+k
2
[2
)-1/2
hkl-"3
а
2
+~
.
Межплоскостное
расстояние
для
плоскостей
(llkO),
па
раллельных
оси
с,
определяетСЯ
выражением
а
мо
=
_
аVз
2Vh
2
+
hk+k
2
ЭЛЕМЕНТЫ
КРИСТАЛЛОГРАФИИ
423
Углы
между
плоскостями
часто
помогают
определить
индексы
рефлекса
на
дифракционной
картине монокристалла.
Меrl\ПЛО
скостные
расстояния
в
электронной
диф
ракции
достаточно
неопре
деленны,
так
что
для
близко
расположенных
рефлексов,
таких,
например,
для
которых сумма
квадратов
индексов
равна
11
и
12
или
19
и
20
в
случае
г.
Ц.
к.
кристаллов,
определенность
может
быть
достигнута
только
проверкой
углов
между
отражениями.
Если
ер
-
угол
между
плоскостями
(h
1
k
1
l
1
)
и
(h
2
k
2
l
2
),
то
тогда
для
орторомБIIческой
системы
(J/1h2/a2) + (k
1
k
2
/b
2
)
+
(l1
l
2/
c2
)
cos
ер
= (
h~
Ч.
li
)1/2
(h~
~l
iL)1/
2
'
(;2+V+
с2
а
2
+
Ь
2
+
с2
для
тетрагональной
системы
[(JLlh2
-+
k
1
k
2
)/a
2
]
+
(ll
l
2/
c2
)
cos
ер
=
(/I~+
Ч
~)1/2
(
h~+Ч
+
l~
)1(2
'
а
2
+
с
2
а
2
с
2
для
кубической
системы
h
1
h
2
+ k
1
k
2
+ ll12
COSep--------~~~~~~--~
-
[(h~+k~+l~)
(h~+k~+lшl/2
'
для
гексагональной
системы
1 3
h
1
h
2
+ k
1
k
2
+ 2 (h
1
k
2
+ h
2
k
1
)
+4
(a
2
jc
2
)
11
1
2
COS
ер
=
-l-C-}L-i-+-
k
-r-+-
h
-l
k-'l-+--i-:--;-:;C--
zi
-)-C-=-,
'-1
~-+-h-.~--t--
-h
2
-k-
2
-+---;:;i:---";n:
-.
l-~:::-)--:J=-Т;-l
/2
•
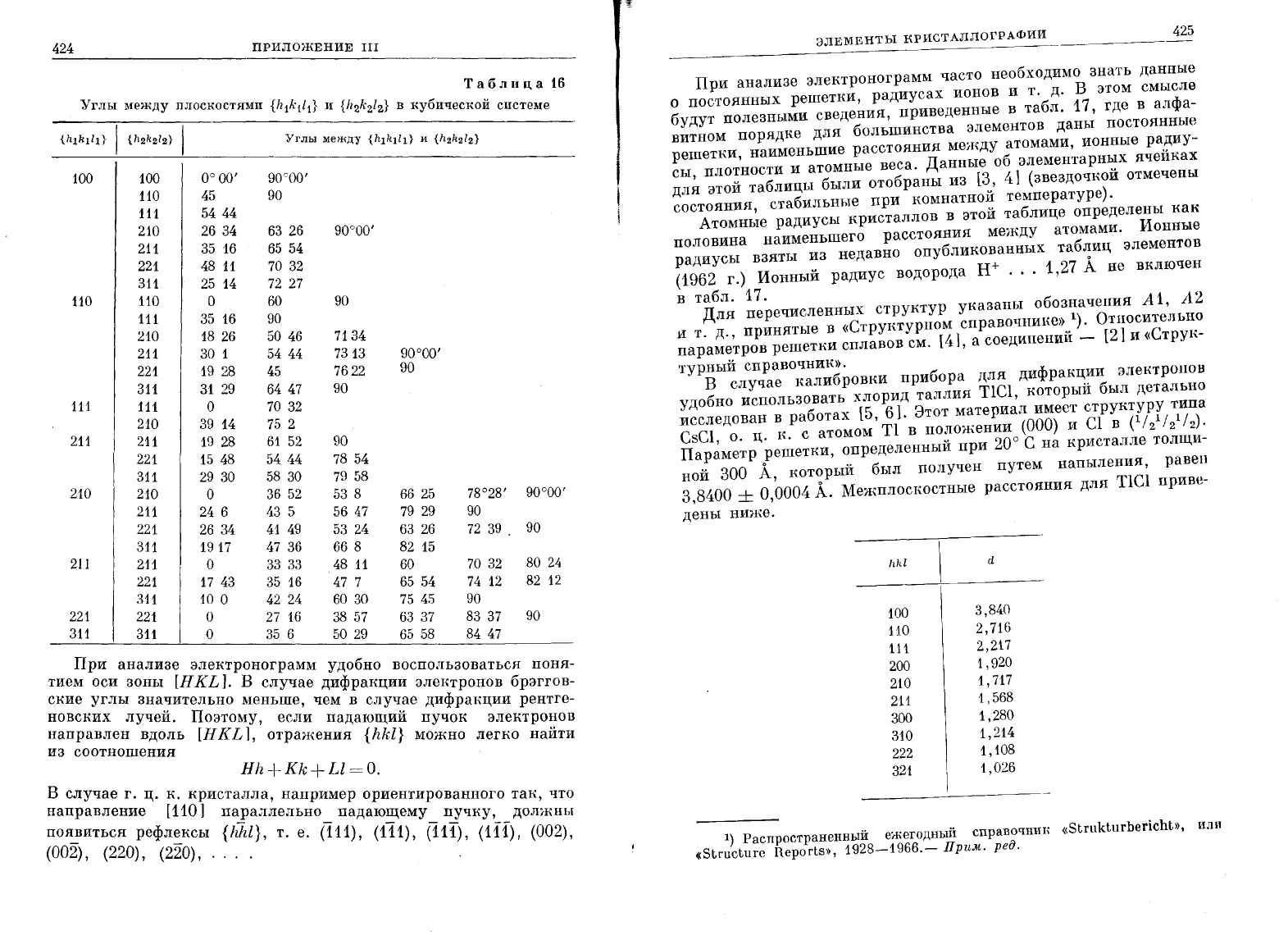
Поскольку
углы
:между
плоскостями
кубической
системы
часто
требуются
при
анализе
электронограмм,
они
приведены
n
табл.
16.
Для
оценки
коэффициентов
Фурье
потенциала
нужны
данные
об
объемах
элементарных
ячеек:
орторомбическая
система:
Q=abc,
тетрагональная
система:
кубическая
система:
Q=a
3
,
гексагональная
система:
а=
~З
а2с=О,866а2с.
Объем,
приходящийся
на
1
а
том,
равен
атомный
вес
.
1024
А
3
=:
Q u
6,02 ·1023
Х
плотность
число
атомов
D
ячеике
424
ПРИЛОЖЕНИЕ
IП
100
100
0000'
90000'
110
45
90
111
54 44
210
26
34
63
26
90000'
211
35
'16
65
54
221
48
11
70
32
311
25
14
72
27
110
110
О
60
90
111
35
16
90
210
18
26
50
46
7134
211
30 1 54 44
7313
90000'
221
19
28
45
7622
90
311
31
29
64
47
90
111
111
О
70
32
210
39
14
75
2
211
211
19
28
61
52
90
221
15
48
54 44
78
54
311
29
30
58
30
79
58
210
210
О
36
52
53
8
66
25
78028'
90000'
211
24
6
43
5 56
47
79
29
90
221
26
34
41 49
53
24
63
26
72
39
90
311
1917
47
36
66
8
82
15
211
211
О
33
33
48
11
60
70
32
80
24
221
17
43
35
16
47
7
65
54
74
12
82
12
311
10
О
42
24
60
30
75
45
90
221
221
О
27
16
38
57
63
37
83
37
90
311
311
О
35
6
50
29
65
58
84
47
При
анализе
электронограм
б
тием
оси
З0НЫ
[Н
KL]
В
м
удо но
ВОСПОЛЬЗ0ваться
поня-
сние
углы
значительн~
Me~~~:ae
дифранции
элентронов
брэггов-
новсних
лучей.
Поэтом
есл'и
чем
в
случ~ае
дифранции
рентге-
направлен
вдоль
[Н
KL
{'
падающии
пучон
элентроноп
И3
соотношения
'
отражения
{hkl}
можно
легно
найти
Hl~+Kk+Ll
=0.
В
случае
г.
ц.
н.
нристалла
на
направление
[110]
,пример
ориентированного
тан,
что
появи
ш:раллельно
_
падающему
пучку,
должны
(002),
T~~;ore~~;~~~.
{hhl},
Т. е.
(111), (111),
(111),
(tП),
(002),
ЭЛЕМЕНТЫ
RРИСТАЛЛОГРАФИИ
425
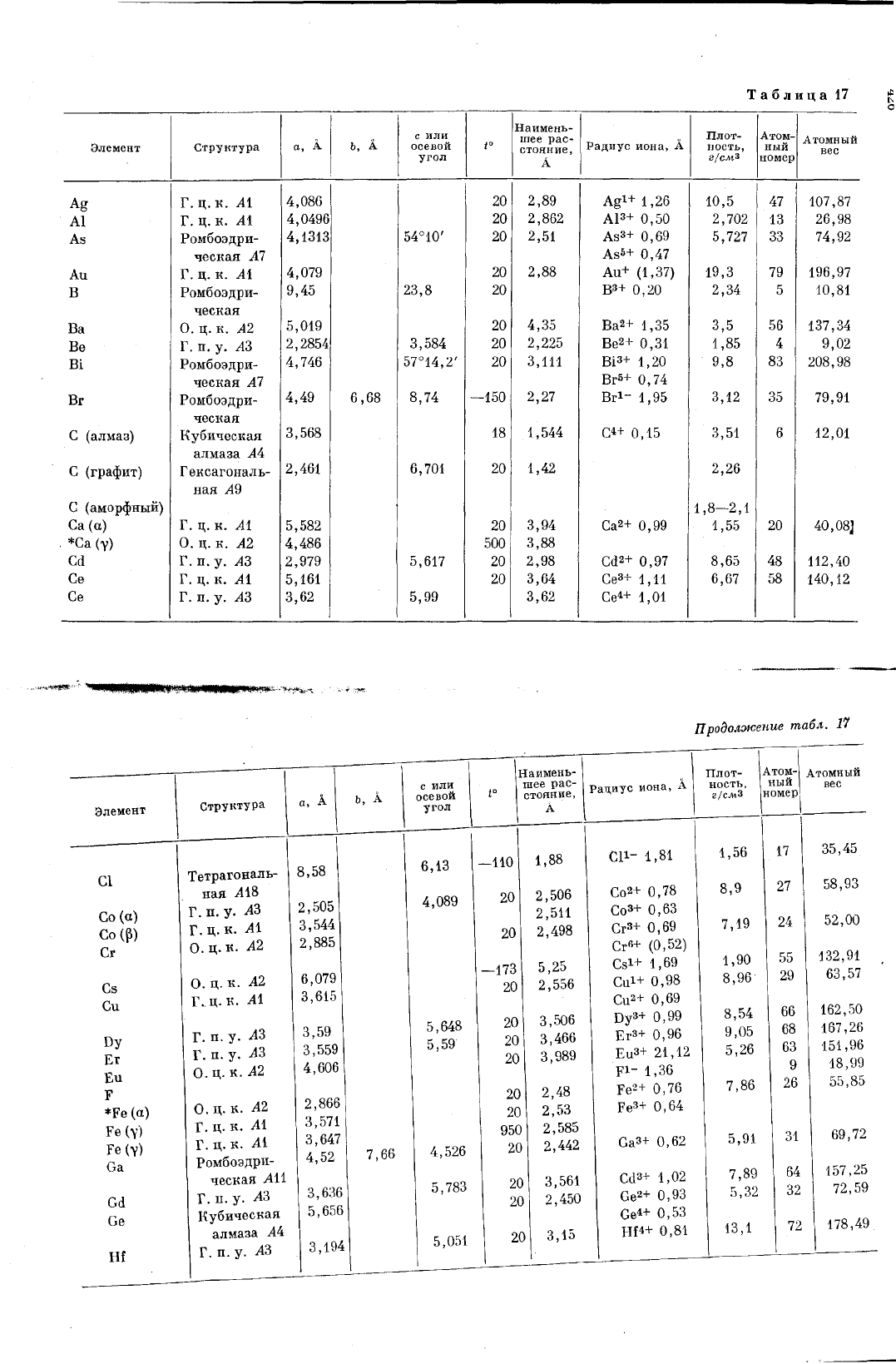
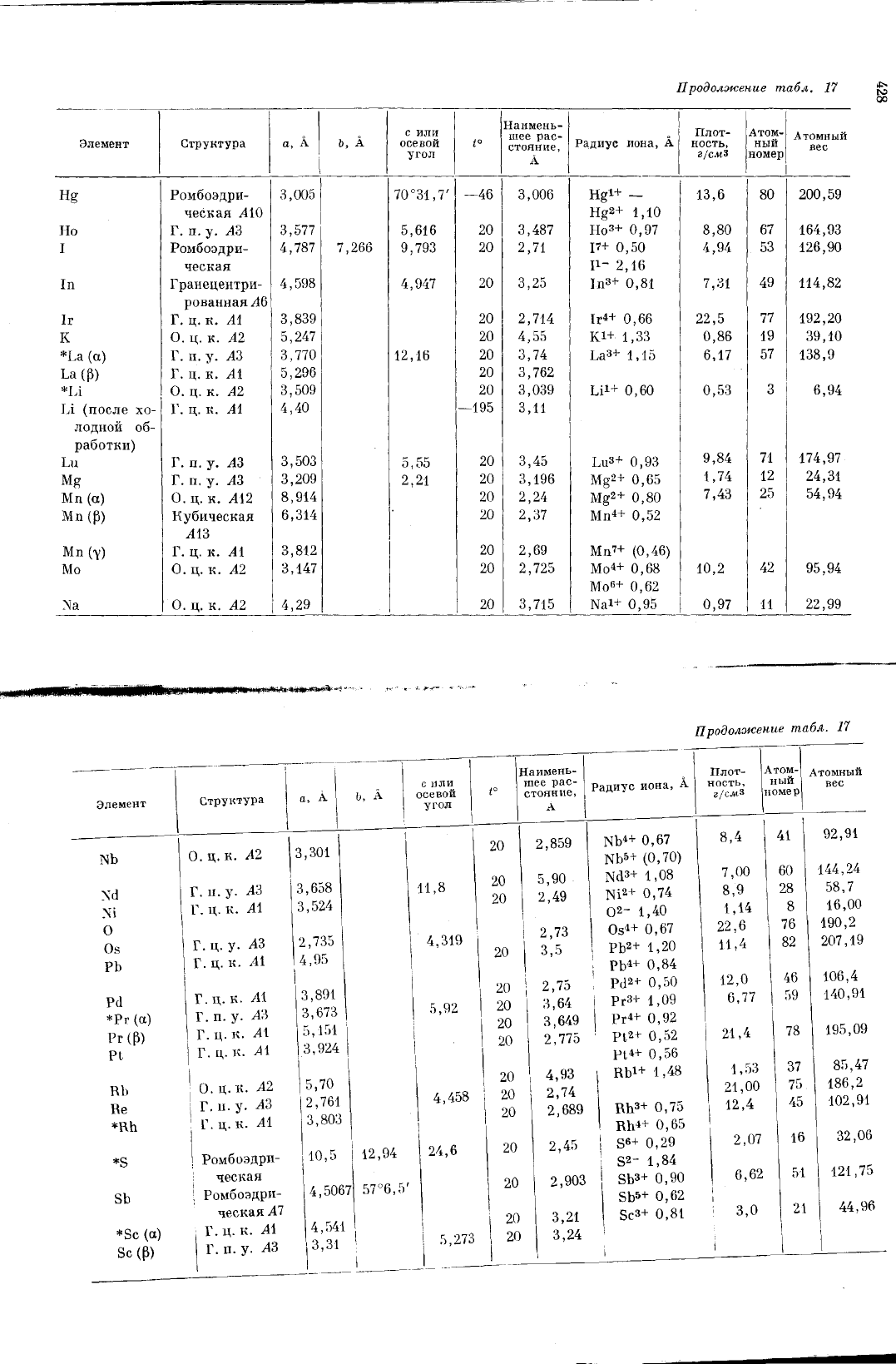
При
анализе
элентронограмм
часто
необходимо
знать
данные
о
постоянных
решетни,
радиусах
ионов
и
т.
д.
Б
этом
смысле
будут
полезными
сведения,
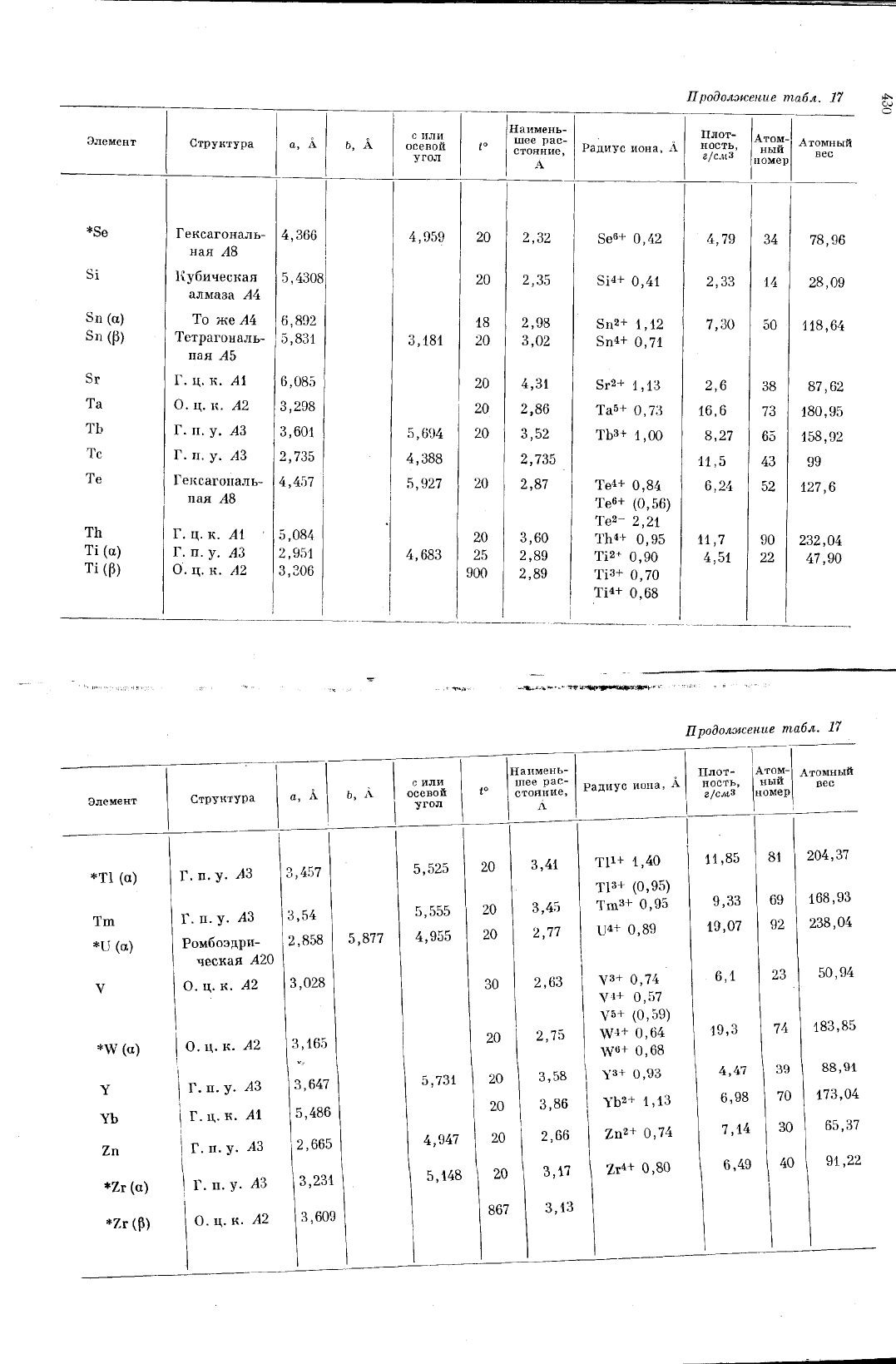
приведенные
в
табл.
17,
где
в
алфа
витном
порядке
для
большинства
элементов
даны
постоянные
решетки,
наименьшие
расстояния
между
атомами,
ионные
радиу
сы,
плотности
и
атомные
веса.
Данные
об
элементарныХ
ячейках
для
этой
таблицы
были
отобраны
И3
[3,
41
(звездочной
отмечены
состояния,
стабильные
при
комнатной
температуре).
Атомные
радиусы
кристаллов
в
этой
таблице
определены
как
половина
наименьшего
расстояния
между
атомами.
Ионные
радиусы
взяты
И3
недавно
опубликованных
таблиц
элементов
(1962
г.)
Ионный
радиус
водорода
Н+
...
1,27
'А.
не
включен
в
табл.
17.
Для
перечисленных
структур
указаны
обозначения
А
1,
А2
11
т.
д.,
принятые
в
«Структурном
спраВОЧНИI{с»
1).
Относительно
параметров
решетки
сплавов
см.
{4],
а
соединений
-
(2]
и
«CTPYI{-
турный
справочнию).
В
случае
калиБРОВI{И
прибора
для
дифракции
электронов
удобно
ИСПОЛЬЗ0вать
хлорид
таллиЯ
TICl,
который
был
детально
исследован
в
работах
{5,
6].
8тот
материал
имеет
структуру
типа
CsCl,
о.
ц.
к.
С
атомОМ
Tl
в
положении
(000)
и
Cl
в
(Ч
2
1J
2
Ч
2)'
Параметр
решетки,
определенный
при
200
С
на
кристалле
толщи-
ной
300
А,
который
был
получен
путем
напыления,
равен
3,8400 + 0,0004
А.
Межплоскостные
расстояния
для
TICl
приве-
дены
ниже.
hkl
d
100
3,840
110
2,716
111
2,217
200
1,920
210
1,717
2'11
1,568
300
1,280
310
1,214
222
1,108
321
1,026
1)
Распространенный
ежегодный
справочнИI{
«Strtlkturbericht),
или
«Structure
Reports}),
1928-1966.-
Прuм.
ред.
Ag
Al
As
Au
В
Ва
Ве
вi
Вг
Элемент
С
(алмаз)
С
(графит)
С
(аморфный)
Са
(а)
,
*Са
(у)
Cd
Се
Се
-
Элемент
Cl
Со
(а)
Со
(~)
Сг
Cs
Cu
Dy
Er
Eu
F
*Fe
(а)
Fe
(у)
Уе
(у)
Ga
Gd
Ge
Hf
Стру«тура
Г.
ц.
Н.
А1
Г.ц.Н.
А1
Ромбоэдри-
чеСRая
А7
Г.ц.Н.
А1
Ромбоэдри-
ческая
О.
ц.
к.
А2
Г. п.
у.
А3
Ромбоэдри-
чеСRая
А7
Ромбоэдри
чеСRая
RубичеСRая
алмаза
А4
Гексагональ
ная
А9
Г.
ц.
Н.
А1
О.
ц. к.
А2
Г.
п.
у.
А3
Г.
ц.
к.
А1
Г.
п. у.
А3
Струнтура
Тетрагональ-
нал
А18
Г.п.у.
А3
Г.
Ц.
Н.
А1
О.
Ц.
Н.
А2
О.
ц. Н.
А2
Г.,ц.н.А1
Г.
п. у.
А3
Г.
п.
у.
А3
О.ц.н.А2
О.
Ц.
Н.
А2
Г.
Ц. Н.
А1
Г. Ц. Н.
А1
Ромбоэдри-
а,
А.
4,086
4,0496
4,1313
4,079
9,45
5,019
2,2854
4,746
4,49
3,568
2,461
5,582
4,486
2,979
5,161
3,62
\
а,
А
\
8,58
2,505
3,544
2,885
6,079
3,615
3,59
3,559
4,606
2,866
3,571
3,647
4,52
чеСRал
А11
Г.
п. у.
А3
3,636
RубичеСRал
5,656
алмаза
А4
Г. п.
у.
А3
3,194
ь, А.
6,68
I
Ь, А.
7,66
с
или
осевой
угол
23,8
3,584
57°14,2'
8,74
6,701
5,617
5,99
\
с
или
осевой
угол
6,13
4,089
5,648
5,59'
4,526
5,783
5,051
Наимень
шее
рас
стояние,
А
20
2,89
20 2,862
20 2,51
20
2,88
20
20
4,35
20
2,225
20 3,111
Радиус
иона,
А
Ag1+
1,26
А13+
0,50
AS3+
0,69
As5+
0,47
Аи+
(1,37)
В3+
0,20
-150
2,27
Ва2+
1,35
ВеН
0,31
Bi
3
+
1,20
Br
5
+
0,74
Br
1
-
1,95
\
18
1,544
20
1,42
20
3,94
500
3,88
20
2,98
20
3,64
3,62
С4+
0,15
Са2+
0,99
Cd
2
+
0,97
Се
3
+
1,11
Се4+
1,01
шее
рас-
о
\наимень-
\
сто~ие,
РадиуС
иона,
А
tO
-110
1,88
Cl
1
-
1,81
20
2,506
Со2+
0,78
2,511
Со3+
0,63
20
2,498
Сг
3
+
0,69
Cr6+
(0,52)
-173
5,25
Cs1+
1,69
20
2,556
Cu1+
0,98
Cu2+
0,69
20
3,506
Dy3+
0,99
20
3,466
Er
3
+
0,96
20
3,989
Eu
3
+ 21,12
Fl-
1,36
20
2,48
Fe
2
+
0,76
20
2,53
Fe3+
0,64
950
2,585
20
2,442
Ga
3
+
0,62
20
3,561
Cd
3
+
1,02
20
2,450
Ge
2
+
0,93
Ge4+
0,53
20
3,15
Hf4+ 0,81
Таблица
17
Плот
ность,
г/сл
3
Атом}
-
ный Атомный
номер
вес
10,5
47
2,702 13
5,727
33
19,3
79
2,34
5
3,5
56
1,85
4
9,8
83
3,12
35
3,51 6
2,26
1,8-2,1
1,55
20
8,65
48
6,67
58
I
107,87
26,98
74,92
196,97
10,81
137,34
9,02
208,98
79,91
12,01
40,08J
112,40
140,12
п
родолжеnuе
табл.
1'1
Плот-
Атом-
Атомный
ность,
ный
вес
г/см3
номер
1,56
17
35,45
8,9
27
58,93
7,19
24
52,00
1,90
55
132,91
8,96'
29
63,57
8,54
66
162,50
9,05
68
167,26
5,26
63
151,96
9
18,99
7,86
26
55,85
5,91
31
69,72
7,89
64
157,25
5,32
32
72,59
13,1
72
178,49
Продолж:enuе
табл.
17
-
Элемент
Структура
а,
А
Ь,
А
е
или
Наимень-
осевой
to
шее
рас-
Плот-
Атом-
угол
стонние,
Радиус
иона,
А
ность,
ный
Атомный
А
г/соМ3
номер
вес
I
Hg
Ромбоэдри-
3'0051
70031,7'
-46
3,006
I
ческая
А10
Hg1+ -
13,6
80
200,59
Но
Г. П.
у.
А3
Hg2+
1,10
3,577
5,616
20
3,487
НоЗ+
0,97
8,80
67
164,93
1
Ромбоэдри-
4,787
7,266
9,793
20
2,71
17+
0,50
4,94
53
126,90
ческая
11-
2,16
In
Гранецентри-
4,598
4,947
20
3,25
In
3
+
0,81
7,:31
49 114,82
РОВaIшаяА6
Ir
Г.
ц.
к.
А1
3,839
20
2,714
Ir4+
0,66
22,5
77
192,20
К
О.
ц. к.
А2
5,247
20
4,55
К1+
1,33
0,86
19
39,10
*La
(а)
Г.
п.
у.
А3
3,770
12,16
20
3,74
La
3
+
1,15
6,17
57
138,9
La
(~)
Г.
Ц.
к.
А1
5,296
20
3,762
*Li ,
О.
Ц. к.
А2
3,509
20
3,039
Li1+
0,60
0,53
3
6,94
Li
(после
хо-
Г.
ц.
к.
А1
4,40
-195
3,11
лодной
об-
I
работки)
Lп
Г. п.
у.
А3
3,503
Mg
Г.
п. у.
А3
3,209
5,55
20
3,45
LuЗ+
0,93
9,84
71
174,97
Mn
(а)
2,21
20
3,196
О.
ц.
к.
А12
8,914
Mg2+
0,65
1,74
12
24,31
20
2,24
M
g
2+
0,80
7,43
25
54,94
Mn
(~)
Кубическая
6,314
20
2,37
Mn4+
0,52
А13
I
Mn
(у)
Г.
ц.
к.
А1
3,812
20
2,69
Mn
7
+
(0,46)
Мо
О.
ц.
к.
А2
3,147 20 2,725
Мо4+
0,68
10,2
42
95,94
Мо6+
0,62
Na
О.
Ц.
к.
А2
4,29
20
3,715
Na1+
0,95
I
0,97
Н
22,99
Продолж:енuе
табл.
17
а.
А
\
Наимень-
плот-
Атом-
е
или
шее
рас-
РадиуС
иона,
А
Атомный
Элемент
Структура
Ь,
А
осевой
tO
СТОRние,
ность,
ный
вес
угол
.А
гjс.м
3
номер
\
1
Nb
О.
ц. к.
А2
\ 3,301
20
2,859
Nb4+
0,67
8,4
41
92,91
Nb
5
+ (0,70)
\"d
Г.
п.
у.
А3
3,658
1'1,8
20
5,90
Nd
3
+
1,08
7,00
60
144,24
~i
Г.
ц.
к.
А1
3,524
20
2,49
Ni
2
+
0,74
8,9
28
58,7
О
02-
1,40
1,14
8
16,00
Os
Г.ц.у.
А3
2,735
4,319
2,73
Os4+
0,67
22,6
76
190,2
РЬ
Г.
ц.
к.
А1
4,95
20
3,5
РЬ2+
1,20
11,4
82
207,19
\
РЬ
4
+
0,84
Pd
Г.
ц. к.
А1
\З,891
20
2,75
Pd
2
+
0,50
12,0
46
106,4
*Рг
(а)
Г.
п.
у.
А3
3,673
5,92
20
3,64
Рг
3
+
1,09
6,77
59
140,91
Рг
(~)
Г. ц.
к.
А1
\5,151
20
3,649
рг4+
0,92
Pt
Г.ц.к.
А1
3,924
20
2,775
Pt
2
+
0,52
21,4
78
195,09
\
Pt4+
0,56
R})
О.
Ц.
к.
А2
5,70
20
4,93
\
Rb1+
1,48
1,5:3
37
85,47
Re
Г.
п. у.
А3
2,761
4,458
\
20
2,74
I
21,00
75
186,2
*Rh
Г.
ц. к.
А1
3,803
20
2,689
\
Rh
3
+
0,75
12,4
45
102,91
I
RhH
0,65
*8
Ромбоэдри-
110,5
12,94
24,6
20
2,45
86+
0,29
2,07
16
32,06
ческа
я
I
82-
1,84
8Ь
:
Ромбоэдри-
4,5067
5706,5'
20
2,903
8Ь
3
+
0,90
6,62
5'1
121,75
ческаяА7
Sb5+
0,62
I
I
1
\
*Sc
(а)
\
Г.
ц. к.
Аl
4,~kl
li
20
3,21
Sc
3
+
0,81
3,0
21
44,96
Sc
(~)
Г.
п.
у.
А3
\3,31
;),273
20
3,24
\
I
I
I
I
i
I
1
ПродОЛ[}fCenuе
табл.
17
Элемент
Струнтура
А
с
или
Наимень-
ATOMJ
а,
Ь,
А
осевой
tO
шее
рас-
Плот-
угол
стонние,
Радиус
иона,
А
ность,
ный
I
Момный
.<\
г/с.м3
номер
вес
I
*Se
Гексагональ-
4,366
4,959
20
ная
А8
2,32
Se6+
0,42
4,79
34
78,96
Si
:Кубическая
5,430В:
алмаза
А4
20
2,35
Si4+
0,41
2,33
14
28,09
Sn
(а)
То
же
А4
6,892
SN
(В)
Тетрагональ-
5,831
18
2,98
Sn
2
+
1,12
7,30
3,181
20
3,02
50
118,64
Sn4+ 0,71
ная
А5
Sr
Г.
Ц.
к.
А1
6,085
20
4,31
Sr
2
+
1,13
2,6
38
87,62
Та
О.
ц.
к.
А2
3,298
20
2,86
Та5+
0,73
16,6
73
180,95
ТЬ
Г.
п. у.
А3
3,601
5,694
20
3,52
ТЬ
З
+
1,00
8,27
65
158,92
Тс
Г.
п.
у.
А3
2,735
4,388
2,735
11,5
43
99
Те
Гексагональ-
4,457
5,927
ная
А8
20
2,87
Те
Н
0,84
6,24
52
127,6
Те6+
(0,56)
Th
Г.
ц.
к.
А1
5,084
Те
2
-
2,21
Ti
(а)
Г.
п.
у.
А3
2,951
20
3,60
Th4+
0,95
11,7
Ti
(В)
4,683
25
90
232,04
О.
ц.
к.
А2
3,306
2,89
Тi2+
0,90
4,51
22
I
900
2,89
ТiЗ+
0,70
47,90
Ti
H
0,68
--
---
----~
____
I~
---
--
-----~--
---1
п
родол;жеnuе
табл.
17
\
Наимень-
Плот-
Атом-
А
ь,
А
с
или
шее
рас-
РадиуС
иона,
А
АтомнЫЙ
Элемент
струнтура
а,
осевой
tO
стонние,
ность,
НЫЙ
вес
\
угол
А
г/с.м,3
номер
1
*Tl
(а)
Г.
п. у.
А3
3,457
5,525
20
3,41
Tl1+
1,40
11,85
81
204,37
T13+
(0,95)
Тт
Г.
п. у.
А3
3,54
5,555
20
3,45
Тm
З
+
0,95
9,33
69
168,93
*u
(а)
Ромбоэдри-
2,858
5,877
4,955
20
2,77
U4+
0,89
19,07
92
238,04
чее:кая
А20
\
V
О.
Ц.:к.
А2
3,028
30
2,63
I
V3+
0,74
6,1
23
50,94
VH
0,57
VH
(0,59)
*w
(а)
О.
Ц.:к.
А2
3,165
20
2,75
W4+
0,64
19,3
74
183,85
W6+
0,68
v.:!
У
Г.
п.
у.
А3
3,647
5,731
20
3,58
\
уз+
0,93
4,47
39
88,91
УЬ
Г.
ц.:к.
А1
5,486
20
3,86
\
УЬ
2
+
1,13
6,98
70
173,04
I
Zn
Г.
п.
у.
А3
2,665
4,947
20
2,66
Zn2+
0,74
7,14
30
65,37
*Zr
(а)
Г.
п.
у.
А3
3,231
5,148
20
3,1.7
Zr4+
0,80
6,49
\
40
91,22
*Zr
(~)
\
О.
Ц. к.
А2
3,609 \
867
3,13
\
\
432
ПРИЛОЖЕНИЕ
III
Хлорид
таллия
ядовит,
и
при
работе
с
ним
необходима
осторож
ность
1).
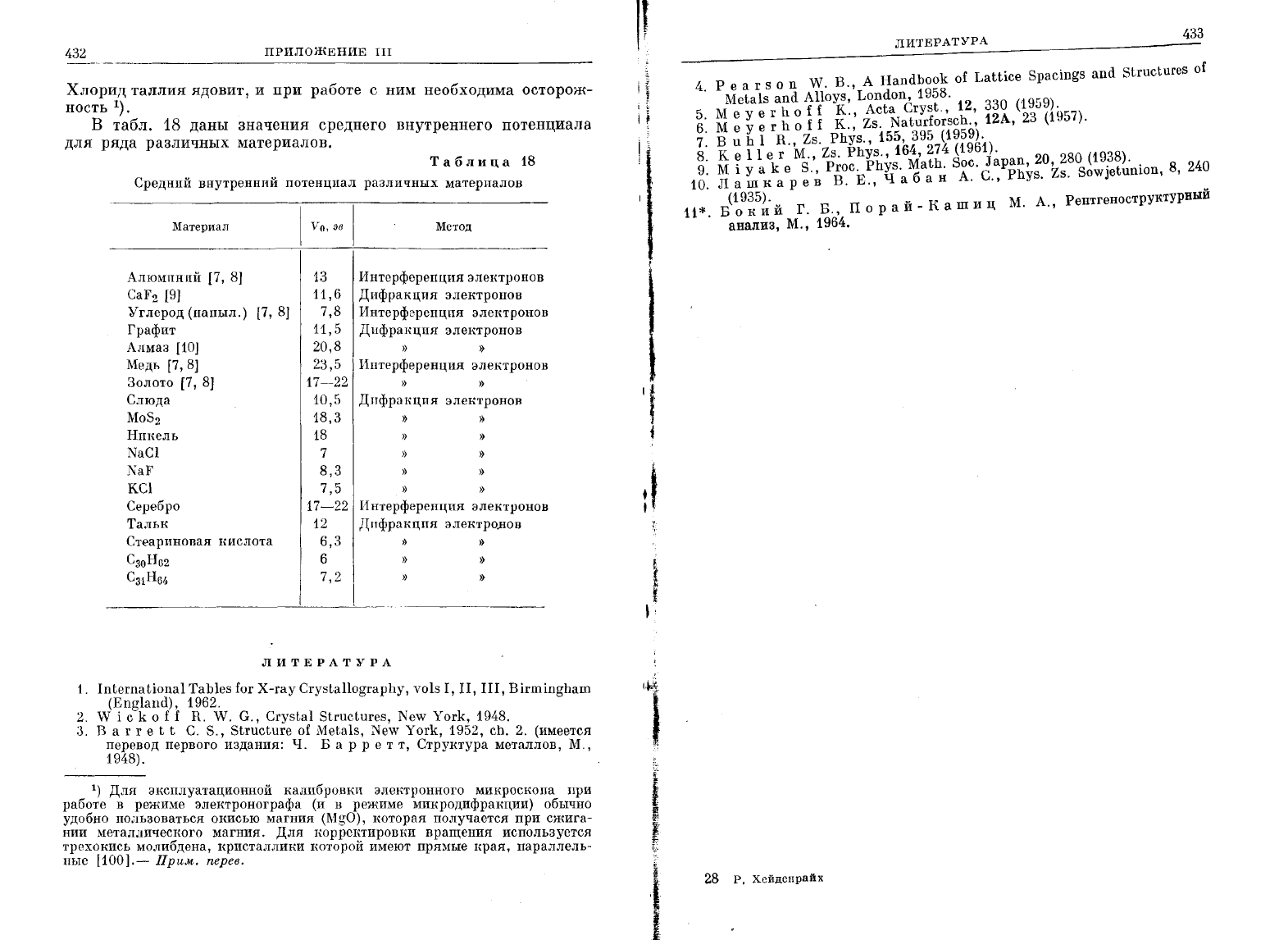
В
табл.
18
даны
значения
среднего
внутреннего
потенциала
для
ряда
различных
материалов.
т
а б
л
и
ц
а
18
Средний
внутренний
потенциал
различных
материалов
Материал
I V,," I
Метод
Алюмпний
[7,
8]
13
Интерференция
электронов
CaF
2
[9]
11,6
Дифракция
электронов
'Углерод
(напыл.)
[7,
8]
7,8
Интерференция
электронов
Графит
11,5
Дифракция
электронов
Алмаз
[10]
20,8
»
»
Медь
[7,8]
23,5
Интерференция
электронов
Золото
[7,
8]
17-22
»
»
Слюда
10,5
Дпфракция
электронов
MoS
2
18,3
»
»
Никель
18
»
»
NaCl
7
»
»
NaF
8,3
»
»
KCl
7,5
» »
Серебро
17-22
Интерференция
электронов
Тальк
12
Дпфракция
электродов
Стеариновая
кислота
6,3
»
С
ЗО
Н
В
2
6
»
»
С
З1
Н
64
7,2
»
»
ЛИТЕРАТУРА
'1
i
1.
International
Tables
for
X-ray
Crystallography,
vols
1,11,111,
Birmingham
I,"~
(England),
1962.~
I~'
2.
W i
с
k
о
f f R. W.
G.,
Crystal
Structures,
New
York,
1948. •
3.
В
а
r r
е
t t
С.
S.,
Structure
of
Меtдls,
New
York,
1952, ch. 2.
(имеется
перевод
первого
издания:
Ч.
Б
а
р р
е т
т,
Структура
металлов,
М.,
~'
1948) .
1)
Для
эксплуатационной
калибровки
элен.ТРОННОГО
микроскоиа
при
работе
в
режиме
электронографа
(и
в
режиме
микродифрющии)
обычно
удобно
пользоваться
окисью
магния
(MgO),
которая
получается
при
сжига
нии
металлического
магния.
Для
корректировки
вращения
используется
трехокись
молибдена,
кристал.лики
которо:й
имеют
прямые
края,
параллель
ные
[100].-
Прuм.
перев.
-
ЛИТЕРАТУРА
433
W
В
А
H
andbook
of
Lattice
Spacings
and
Structures
о!
4. Р
е
а
r s
оп.
. ,
Metals
and
Alloys,
London,
1958. 12 330 (1959)
5
Meyerhoff
К.,
Acta
Cryst.,
, (1957)
6'
М
е
у
е
r h
о
f f
К.,
Zs.
Naturforsch.,
12А,
23
.
7:
в
u h 1
R.,
Zs.
Phys.,
1551'6439527(419(f2~1)
8.
Keller
М
Zs
Phys.,
, .
80(1938)
9.
М
i
У
а
k
е
S.',
Р;ос.
Phrt·
~ath.
S1
c
.
Jap~~y;.Oz;.
SowjetU:nion, 8, 240
10.
Лашкарев
В.
Е., а
ан
..
,
(1935).
u u
М.
А.,
РентгеноструктУРНЫЙ
11*. Бокий
Г.
В.,
Пораи-nашиЦ
анализ,
М.,
1964.
28
Р,
Хейденрайх

ПРИЛОЖЕНИЕ
IV
При
мер
иа
динамической
треХВОdНОВОЙ
теории
В
некоторых
частных случаях
можно
найти
приближенное
решение
дисперсионного
уравнения
(8.4а)
при
наличии
трех
сильных
волн.
Обозначим
амплитуды
сильных
волн
через
С С
и
Св'
Тогда
уравнение
(8.4а)
примет
вид
о,
g
(
ЕО-Е
-
V_
g
-
V-
s
)(Со)
- V
g
Eg-E
- V
g
-
s
C
g
=0.
- V
s
- V
S
-
g
Ев-Е
С
В
(lV.1a)
При
этом
равна
нулю
амплитуда
C
g
-
s
,
соответствующая
коэффи
циенту
V
g
-
s
в
уравнении
(IV.1a).
Последнее
отвечает
симметрич
ному
случаю,
когда
s =
-g
и
величиной
V
s
-
g
в
первом
прибли-
жении
можно
пренебре~~_
Если
g = (111), s =
(111),
то
g -:- S
есть
(222),
а
s - g
e~~
_(222).
Векторы
g - s
й
s - g,
отвечающие
рефлексам
(222)
и
(222),
характеризуют
собой
систематические
отражения
более
высокого
порядка.
Полагая
V
и
V
р
g-s
s-g
ав-
ными
нулю,
получаем
секулярное
уравнение,
в
котором
векторы
g
и
s
удовлетворяют
условию
Лауэ:
Ео-Е
--V_
g
-V-
s
-V
g
Ео-Е
О
-V
s
О
Ео-Е
Три
К0РНЯ
этого
определителя
равны
Ео<О)
-
Е
=
О
=
дЕ<О)
О ,
(IV.1б)
E~1)
-Е
=
IJ.E~1)
= -
Vrl
V
g
12
+ I V
s
12
, (IV.2a)
E~2)
-
Е
=
IJ.Е62)
= +
VI
V g
12
+ I V
s
12
.
В
том
случае,
когда
обе
дифрагированные
волны
удовлетво
яют
условию
Брэгга,
возмущение
.приводит
к
расщеплению
вы
01:
ен-
ного
уровня
Е
на
три
уровня:
Е<О)
ЕШ
Е(2)
В
Р Д
чае
Е<О)
Е
О'
О
И
О'
данном
слу-
О
=
И
поэтому
трем
поверхностям
дисперсии
отвечают
11
I
ПРИМЕР
ИЗ
ДИНАМИЧЕСКОЙ
ТРЕХВОЛНОВОЙ
ТЕОРИИ
три
энергетические
щели.
Третья
щель
равна
дЕ
12
=
!J.E~2)
-
ДE~1).
Соответствующее
приращение
волнового
вектора
есть
IJ.К
12
=
2~
дЕ
12
=
~
VIV
g
\2+IV
s
\2.
435
(IV.2б)
Используя
граничные
условия
в
системе
(IV
.1а),
получаем
выра
жения
для
амплитудных
коэффициентов:
C~O)
=
о,
АЕ<Н
АЕ(2)
С
Ш
___
и_о
_
С(2)
=
_и_о_
,
О
- l:!E
12
,
о
L\E
12
Ш
V
g
(2)
V
g
C
g
= -
L\E
12
, C
g
=-.
l:!E
12
'
С
Ш_-~
C(2)~~
s - l:!E
12
' s l:!E 12 •
C~O)
=
о,
Соответствующие
три
волновые
функции
имеют
вид
(IV.За)
В
интересующем
нас
случае
s = - g
интенсивности
выражаются
в
виде
1
I
Ч'т
\2
= cos
2
2"
дК
12
Z
'
\
12
_ 1 V g
12
,. 2 1
АК
_ 1 . 2
i.
А
К
Ч'g
I
.-
\ V g
12
+ \ V
_g
\2
Sln
2"
Lj
12
Z
-
2"
Sln 2
Lj
12
Z
,
(Iv.Зб)
1
Ч'-g
\2=-
~
sin
2
~
ДК
12
z.
Закон
Фриделя
1)
выполняется,
поскольку
при
выводе
форму
лы
(IV
.За)
предполагалось
наличие
центра
симметрии.
При
рассеянии
на
совершенном
кристалле,
когда
падающий
пучок нормален
R
сечению
обратной
решетки,
содержащему
век
торы
g
и
_g,
оба
вектора
будут
находиться
на
сфере
Эвальда.
Если
же
кристалл
имеет
цилиндрический
иагиб,
то,
как
показано
на
фиг.
178,
узлы
обратной
решетки
превращаются
в
дуги.
На
электронном
изображении,
соответствующем
фиг.
178,
будут
проявляться
два
изгибных
контура
экстинкции,
в
В
И
С,
соот
ветственно
узлам
обратной
решетки
G
и
-G.
1)
См.
F.
Fujim:oto,
Journ.
Phys.
Soc
..
Таран,
14,1558
(1959).
28*

436
ПРИЛОЖЕНИЕ
IV
Нсточник
конечных
размеров
а
-r~--~~~~~~~--~~====~J[~1-Нул~ой
,роввнь
g
..
:
и
г.
178.
а
-
цилиндрически
иаогнутый
кристалл
с
радиусом
иагиба
ели
диаметр
ИСточнииа
в
плосиости
объеRта
В
е
удовлетворяет
условию
р
<
в
lr g
I~:
то
Появятся
нонтуры
В
областях
В
и
С.
е,
б
-
представление
обратной
решетки
для
рефлексов
g
и
_g
в
дуги
порядка
1/2
(В
/Q). '
растянутых
Если
расходи:мостъ
падающего
ПУЧRа
Удовлетворяет
у~ловию
{:J
>-
у.
r g I
л
(&1
вина
угла
расходи:мости)
то
для
й
..
s
---
2
1-'
8 -
поло-
ЗИСТИНRЦионная
длина
б
'дет
оп
е
луче
,
распространяющихсл
под
углами
1±
У.
I g I
л
распространяющегося
в~олъ
tcи:де~:~;~:и~~рмулами
двухволноВой
теории.
д~я
луча'
трехволновой
о~~~~и:~ли:на
определяется
по
формулам
Пр~
источнике
излучения
конечных
размеров
можно
предста
вить
се
е,
что
изображение
ВОзникает
в
результате
пре
ессии сфе
ры
Эвальда
относительно
нулевого
узла.
Для
участка
6
на
сфе
~
лежат
точки
0u
и
G,
а
для
участка
В
-
точки
О
и
-G.
Размыт~е
узлов
обратнои
решетки
в
дуги
приводит
К
тому
что
распространяюще
u ,
для
Волны
об
G
ися
в
направлении,
совпадающем
с
осью
пучка'
е
точки
и
-G
касаются
сферы
Эвальда.
'
В
Положении
С
(на
контуре)
ЭКСТИНКЦИонная
длина ля
изл
чения,
распространяющегося
не
по
оси,
близка
к
значе:ию
у-
лЕ
tO=-тт
,
. g
ПРИМЕР
из
ДИНАМИЧЕСНОЙ
ТРЕХВОЛНОВОЙ
ТЕОРИИ
437
так
же
как И
на
контуре
В.
Но
для
излучения,
распространяю
щегося
вдоль
направления
оси
падающего
пучка,
экстинк
ционная
длина
равна
t'
_
лЕ
0-
V
g
V2
.
Следовательно,
при
источнике
конечных
размеров
(фиг.
105)
профи
ли
интенсивности
нессиметрично
пересекают
контуры
экстинкции.
Если
кристалл
тонкий
и
слегка
клинообразный,
то
число
допол
Elительных
максимумов
будет
увеличиваться
через.
каждый
интер
вал
толщины,
соответствующий
экстинкционной
длине.
Область
между
контурами
будет
более
темной,
чем
области
вне
контуров.
Так
как обычно
в
изогнутых
кристаллах
реализуется
более
одной
экстинкционной
длины,
то
при
интерпретации
контуров
экстинкции
в
этих
кристаллах
необходима
большая
осторожность.
Если
же
изогнутый
кристалл
достаточно
толстый
для
того,
чтобы
образовывались
линии
Rикучи,
то
мошно
установить
направление
изгиба
-
выпуклость
или
вогнутость
кристалла.
Интенсивность
линий
Rикучи
будет
максимальной,
если
точно
выполняется
условие
Брэгга и
плоскости,
участвующие
в
обра
зовании
линий
Кикучи,
параллельны.
Таким
образом,
при
исполь
зовании
малой
селекторной
диафрагмы
область
В
будет
участво
вать
в
образовании
светлых
линий
Кикучи,
которые
расположены
дальше
от
нулевой
точки
(фиг.
178),
чем
брэгговский
рефлекс
-G.
Область
С
также
будет
участвовать
в
образовании
светлой
линии,
расположенной
дальше
от
нуля,
чем
брэгговский
рефлекс
G.
Если
бы
кристалл
был
расположен
выпуклостью
вверх,
то
светлая
линия
Кикучи
была
бы
ближе
к
нулевой
точке
или
лежала
бы
между
соответствующими
брэгговскими
рефлексами.
Если
в
дифракционной
картине
имеются
как
брэгговский
рефлекс,
так
и
связанная
с
ним
линия
Кикучи,
то
~
расстоянию
между
рефлексом
и
линией
легко
определить
отклонение
рефлекса
от
угла
Брэгга.
Если
темная
линия
смещается
из
нулевой
точки
на
то
же
расстояние
и
в
том
же
направлении,
что
и
светлая
линия,
то
кристалл
отклоняется
от
точного
угла
Брэгга
на
угол
лl'1R
ДО
=-
---п:-
рад,
где
д,R
-
линейное
расстояние
па
диффракционной
картине
между
брэгговским
рефлексом
и
светлой
линией
Rикучи.
Отклоне
ние
от
условия
Брэгга,
выраженное
в
элеКТРОJIвольтах,
имеет
вид
лЕ
л
2
ЕI'1R
д'=-d-
ДО
=
(Lл)d
'
где
d -
межплоскостное
расстояние.
Если
же
линия
Кикучи
расположена
дальше
от
нуля,
чем
брэгговский
рефлекс,
то
вели
чина
s =
gД,е
положительна
(см.
фиг.
98) .

ПРИЛОЖЕНИЕ
V
Опреде.JIепие
вектора
Бюргерса
в
гл.
9
было
показано,
что
особенности
контраста,
обуслов
ленного
наличие~
дефекта
в
кристаллической
решетке,
опреде
ля~т~
величинои
(gb)
или
(gUj) ,
где
g -
вектор
обратной
решетки
а
-
П!
-
смещение
атома,
вызванное
дефектом.
Величин~
(gb)
есть
проекция
смещения
Ь
на
направление
вектора
обратной
решетки
g.
Плоскости
кристаллической
решетки,
в
которых
лежит
вектор
Бюргерса
дефекта
Ь,
удовлетворяют
условию
(gb) -
О
и
не
подвержены
искажениям,
обусловленным
наличием
эт~го
дефекта.
Вектор
Бюргерса
является
отрезком
линии
в
пря
мои
решетке
и
поэтому
определяется
геометрическим
местом
пересечения
двух
или
больше
плосн:остеЙ.
Таким
образом
если
известны
миллеровские
индексы
двух
плоскостей,
пересе~ением
которых
определяется
вектор
Бюргерса,
то
тем
самым
фактически
определен
и
вектор
Бюргерса.
Пусть
g
и
g'
б
u
-
векторы
о
ратнои
решетки,
соответствующие
двум
отражениям,
в
которых
контраст
от
данного
дефекта
равен
нулю.
Тогда
,
(gb) =
О,
(g'b)
=
О,
(V.1a)
или
в
обозначениях
прямой
решетки
(а
а а
б
ячейки
в
прямой
решетке):
f,
2,
3 -
длины
ре ер
(V.1б)
Здесь
Ь
1
,
Ь
2
,
Ь
З
_.
компоненты
вектора
Бюргерса.
Если
падающий
пучок
электронов
параллелен
оси
зоны
[HKLJ
тонкого
кристалла
то
для
ПЛОСКостей
(отражений)
(hkl)
и
U/"k'l')
выполняютс~
l'
,
условия
ОПРЕДЕЛЕНИЕ
ВЕКТОРА
БЮРГЕРСА
IlH
+kK
+lL=O,
Il'H
+k'K
+
l'L
=0.
439
(V.1B)
Таким
образом,
после
того
как
определена
ось
зоны,
при
помощи
выражений
(У.1в)
может
быть
.Проиндицирована
дифракционная
картина
и
определен
вектор
Бюргерса,
удовлетворяющий
усло
виям
(У.1а)
или
(V.1б).
Методически
это
может
быть
осуществлено
при
систематическом
темнопольном
исследовании
дифракционных
пятен
для
нахождения
тех
из
них,
контраст
от
дефекта
в
которых
равен
нулю.
Такой
метод
был
использован
В
работе
[1]
при
ана
лизе
дислокационных
сеток
в
теллуриде
висмута.
С
другой
сто
роны,
используя
методику
наклона
образца,
можно
вывести
объект
в
такое
положение,
при
котором
контраст,
обусловленный
исследуемым
дефектом,
станет
равным
нулю.
При
этом
индексы
дифракционных
пятен
на
электронограмме,
ПОJlучеНIIОЙ
от на
клоненного
кристалла,
будут
удовлетворять
соотношениям
(У.1а)
и,
таким
образом,
будет
определен
вектор
Бюргерса
дефекта.
В
том
случае,
когда
есть
сомнения,
точно
ли
равен
нулю
кон
траст,
весьма
полезна
пере
крестная
проверка,
которая
мошет
быть
осуществлена
комбинацией
этих
двух
методов
определения
вектора
Бюргерса.
Если
микроскоп
скорректирован
на
магнитное
вращение
изображения,
то
при
совмещении
электронно-микроскопического
изображения
с
картиной
микродифракции,
полученной
с
того
же
места
образца,
на
изображении
могут
быть
определены
криста.тI
лографические
напраВ.тIения.
Для
большинства
случаев
этого
оказывается
достаточно,
так
как абсолютное
соответствие
кри
стаЛ.тIографических
направлений
не
имеет
большого
смысла.
Но
в
некоторых
С.тIучаях
бывает
необходимо
получить
ПО.тIное
соответст~ие
кристаллографических
направлений,
т. е.
точно
определить
их
в
объекте
и найти на
изображении.
Это
дости
гается
поворотом
конечного
изображения,
скорректированного
на
магнитное
вращение
промежуточной
.тIинзы,
на
1800
относи
тельно
центра
изображения.
Необходимость
такого
добавочного
поворота
очевидна
из
фиг.
64.
При
использовании
метода
микро
дифракции
промежуточная
линза
устанаВ.тIивается
так,
чтобы
получить,
например,
рефлекс,
соответствующий
вектору
обратной
решетки
01
(см.
фиг.
64).
При
этом
магнитное
вращение
относи
Te.тIЬHO
объекта
равно
Ур'
При
уве.тIичении
оптической
СИ.тIЫ
проме
жуточной
линзы
ПО.тIучается
уве.тIиченное
изображение
О
p~,
сум
марное
магнитное
вращение
которого
равно
Yi'
Относительное
магнитное
вращение
между
изображением
и
дифракционной
Н.ар
тиной
У;
-
Ур
определено
калибровкой
прибора.
Но
расстояние
OP~
перевернуто
относительно
расстояния
OP~
в
объекте,
а
также
440
ПРИЛОЖЕНИЕ
V
относительно
вектора
обратной
решетки
01.
Следовательно,
если
окончательное
изображение
ОР;
ОТНОсится
к
расстоянию
OP~
в
объекте,
то
изображение
должно
быть
повернуто
на
1800,
кю{
это
было
показано
в
работе
[21.
Необходимость
определения
абсолютного
направления
век
тора
Бюргерса
возникает,
например,
тогда,
когда
нужно
опреде
лить
различие
между
вакансионной
петлей
и
петлей
дефекта
внедрения
[3].
в
случае
таких
дефектов
решетки
основной
метод
изучения
-
контролируемый
наклон
кристалла
(объекта).
Если
при
ИСПОЛьзовании
Этого
метода
угол
наклона
образца
превыmает
несколько
градусов,
то
в
выражении
(9.4е)
должно
быть
учтено
эффективное
увеличение
толщины
(конечно,
только
тогда,
когда
это
выражение
используется
для
оценки
светлопольного
кон
траста).
Отклонения
от
условия
Брэгга
при
этом
получаются
IHKLJ
~
@
х
о
Пл~с/{осmь
oozeHma
------~r_-~-
____
Ее
Е
3аdНRЯ
фокальная
О
g G
плоскость
е
x
i
"'""'C
___
.~_-.-~_~.....;.
___
---.....
(±)ж
i
Плоскость
~
О
Ь]
uзо6ражения
+г'
ОптuчеснаJl
ось
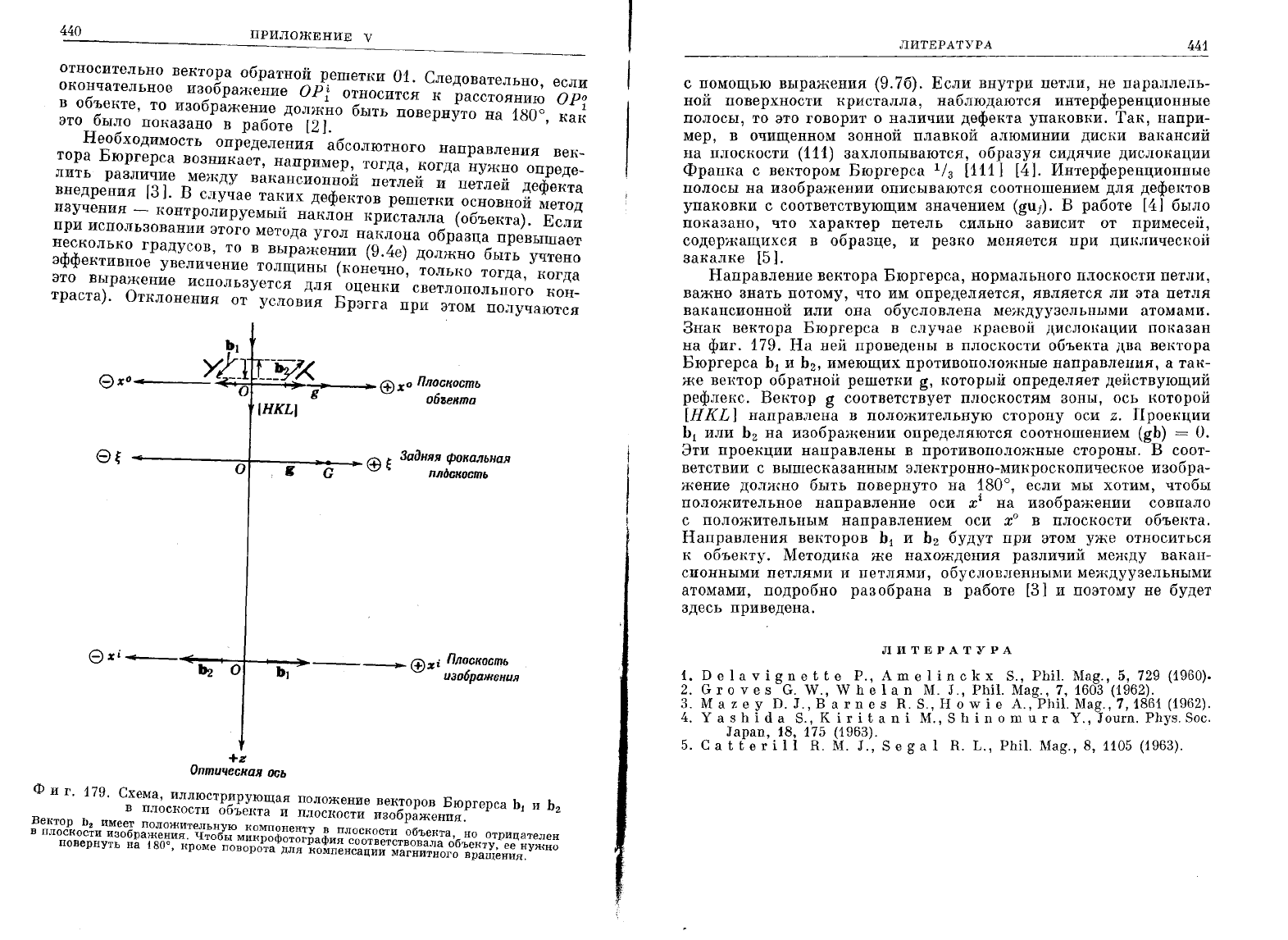
фиг.
179.
Схема,
иллюстрирующая
Положение
BeRTopoB
Бюргерса
Ь
1
и
Ь
2
В
ПЛОСRОСТИ
объекта
и
плоскости
изображения.
Вектор
Ь
2
имеет
положительную
компоненту
в
ПЛОСКОСти
объекта
но
От
и
ателен
в
ПЛОСI<ОСТИ
ИЗОбражения.
Чтобы
МИI<РОфотографИя
Соответствовала
объекту
РееЦнужно
повернуть
на
1800,
Ироме
поворота
Для
компенсации
магнитного
вращения.
ЛИТЕРАТУРА
441
с
помощью
выражения
(9.
7б).
Если
внутри
петли,
не
параллель
ной
поверхности
кристалла,
наблюдаются
интерференционные
полосы,
то
это
говорит
о
наличии
дефекта
упаковки.
Так,
напри.:
мер,
в
очищенном
зонной
плавкой
алюминии
диски
вакансии
на
плоскости
(111)
захлопываются,
образуя
сидячие
дислокации
Франка
с
вектором
Бюргерса
lJ
З
[111]
[4].
Интерференционные
полосы
на
изображении
описываются
соотношением для
дефентов
упаковки
с
соответствующим
значением
(gUj).
В
работе
[4]
БЫJ~.,о
показано,
что
характер
петель
сильно
зависит
от
примеС8}~?
содержащихся
в
образце,
и
резко
меняется
при;
цинличеснои
закалке
[5].
Направление
вектора
Бюргерса,
нормального
плоскости
петли,
важно
знать
потому,
что
им
определяется,
является
ли
эта
петля
вакансионной
или
она
обусловлена
междуузсльными
атомами.
Знак
вектора
Бюргерса
в
случае
краевой
ДИСЛОl\аЦИИ
показан
на
фиг.
179.
На
ней
проведены
в
ПЛОСIШСТИ
объекта
два
вентора
Бюргерса
Ь
1
и
Ь
2
,
имеющих
ПРОТИВОПОJIожные
направле.~IИЯ,
а
так
и
-
же
вентор
обратной
решетни
g,
ноторый
определяет
деиствуIOЩИ~
рефлекс.
Вектор
g
соответствует
плоскостям
зоны,
oc~
которои
[Н
KL]
направлена
в
положительную
сторону
оси
z.
IIроекции
Ь
1
или
Ь
2
на
изображении
определяются
соотношением
(gb) =
О.
Эти
проекции
направлены
в
противоположные
стороны.
В
соот
ветствии
с
вышесказанным
ЭJIектронно-микроскопическое
изобра
жение
должно
быть
повернуто
на
t80°,
если
мы
хотим,
чтобы
положительное
направление
оси
x~
на
изображении
совпало
с
положительным
направлением
оси
х
О
в
плоскости
объекта.
Направления
векторов
Ь
1
и
Ь
2
будут
при
этом
u
уже
относиться
к
объекту.
Методика
же
нахождения
различии
между
вакан
сионными
петлями
и
петлями,
оБУСЛОВJlенными
междуузельными
атомами,
подробно
раз
обрана
в
работе
[3]
и поэтому
не
будет
здесь
приведена.
ЛИТЕРАТУРА
1.
De1avignette
Р.,
Amelinckx
S.,
Phil.
Mag., 5, 729 (1960).
2. G r
о
v
е
s
G.
W.,
W h
е
1
а
n
М.
Х.,
Phil.
Mag., 7, 1603 (1962).
3.
М
а
z
е
у
D.
J.,
В
а
r n
е
s R. S.,
Н
о
w i
е
А.,
Phil.
Mag., 7, 1861 (1962).
4.
У
а
s h i d
а
S.,
к
i r i t
а
n i
М.,
S
11
i n
о
m u r
а
У.,
J ourn.
Phys.
Soc.
J
арап,
18, 175 (1963).
5.
С
а
t t
е
r i
11
R.
М.
Х.,
S
е
g
а
1 R.
L.,
Phil.
Mag., 8, 1105 (1963).
