Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление

Подождите немного. Документ загружается.

3.7. Выводы 101

монотонно убывает — в отличие от просто устойчивых систем, для которых норма

убывает в асимптотике, а при малых t возможен всплеск (резкий рост траекто-

рии).

Аналогичными свойствами обладает и дискретная система, матрица A = ((a

))

которой дискретно сверхустойчива, т.е. для которой kAk

< 1 (Теорема 19). Для

дискретного случая имеется одномерный аналог сверхустойчивости, именно, поли-

ном P (z) = p

+. . . +p

z +p

называется сверхустойчивым, если

i=1

| < |p

при этом для скалярной системы, заданной разностным уравнением, соответству-

ющим полиному P (z), аналогичные результаты даются Теоремой 22.

Если в нестационарной системе ˙x(t) = A(t)x(t) матрица A(t) сверхустойчива при

любом фиксированном t, то система сверхустойчива, Теорема 21 (этот вывод со-

вершенно неверен применительно к устойчивости).

Поскольку сверхустойчивость формулируетсая в терминах элементов матриц, то

она неинвариантна относительно преобразования координат, т.е. может теряться

или, наоборот, приобретаться в новых координатах.

102 Глава 3. Устойчивость

Глава 4

Стабилизация

В предыдущей главе обсуждалось важнейшее понятие устойчивости линейных си-

стем. Однако открытая система может быть неустойчивой; тогда можно пытаться до-

биться устойчивости замкнутой системы путем введения обратной связи. Различные

способы подобной стабилизации исследуются в настоящей главе.

4.1 Стабилизация с помощью регуляторов низкого по-

рядка

Пусть одномерный объект записывается с помощью передаточной функции

G(s) =

A(s)

B(s)

, A(s) = a

+ a

s + . . . + a

, B(s) = b

+ b

s + . . . + b

, m ≤ n.

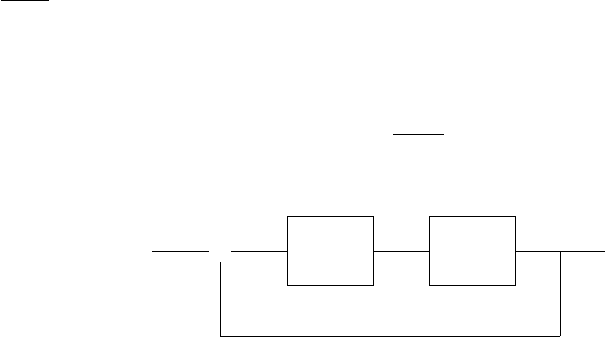
Мы хотим замкнуть систему с помощью регулятора (см. рис. 4.1)

C(s) =

N(s)

D(s)

так, чтобы замкнутая система была устойчивой. Как мы знаем, характеристический

G(s)

C(s)

Рис. 4.1: Стабилизирующий регулятор.

полином имеет вид

P (s) = A(s)N(s) + B(s)D(s).

Таким образом, нужно выбрать полиномы N(s) и D(s) так, чтобы P (s) был гурвицевым.

В такой постановке мы рассмотрим задачу в разделе 4.2, а сейчас рассмотрим ситуации,

когда C(s) имеет простейший вид и зависит от одного-двух параметров.

103

104 Глава 4. Стабилизация

4.1.1 П-регулятор

Наиболее элементарным представляется случай, когда C(s) — пропорциональный

регулятор (П-регулятор): C(s) = k, и выбору подлежит коэффициент усиления k > 0.

Характеристический полином имеет вид

P (s) = B(s) + kA(s),

и его корни являются функциями от k (при k = 0 они совпадают с корнями B(s), а

при k = ∞ — с корнями A(s)). Можно исследовать поведение этих корней графически;

такой метод называется методом корневого годографа. Однако в двух важных частных

задачах решение находится проще.

а. Устойчивый объект (полином B(s) устойчив). Тогда разомкнутая система устой-

чива, и в принципе нет нужды во введении обратной связи. Однако в ряде задач об-

ратная связь вводится для других целей; более того, важно иметь как можно более

высокий коэффициент усиления. Характеристический полином P (s) = B(s) + kA(s)

устойчив при малых k (поскольку B(s) устойчив); вопрос заключается в том, каково

критическое значение k, при котором происходит потеря устойчивости. Ответ на него

немедленно следует из критерия Найквиста. Действительно, там мы рассматривали

объект с передаточной функцией G(s ) и единичную обратную связь, а вышеприведен-

ная задача эквивалентна объекту с передаточной функцией kG(s) и также единичной

обратной связью. Вспоминая формулировку критерия Найквиста для устойчивого объ-

екта, и проводя “масштабирование” вещественной оси, получаем критерий устойчиво-

сти.

Теорема 23 Объект с устойчивой передаточной функцией G(s) и коэффициентом

усиления k в цепи обратной связи устойчив тогда и только тогда, когда годограф

Найквиста G(jω) не охватывает точки − 1/k.

ﬁgure=c:/sher/book/ﬁgs/4nyq.eps,height=2.5in,width=3.5in

Рис. 4.2: Критический коэффициент усиления.

Таким образом, один и тот же годограф решает вопрос об устойчивости для любых

значений k. Более того, немедленно решается и задача о максимальном k:

k = −

где κ — точка самого левого пересечения G(jω) с отрицательной вещественной полу-

осью, рис. 4.2, слева. Это объясняет термин “запас по амплитуде”, введенный в Гл. 3.

Отметим, что в некоторых случаях — если G(jω) не пересекается с отрицательной

полуосью — k = ∞ (рис. 4.2, справа), т.е. возможны сколь угодно большие коэффици-

енты усиления, сохраняющие устойчивость замкнутой системы.

Пример 4.1 Рассмотрим цепочку n одинаковых звеньев первого порядка с передаточ-

ной функцией W(s) = 1/(1+T s), T > 0, соединенных обратной связью с П-регулятором

(рис. 4.3).

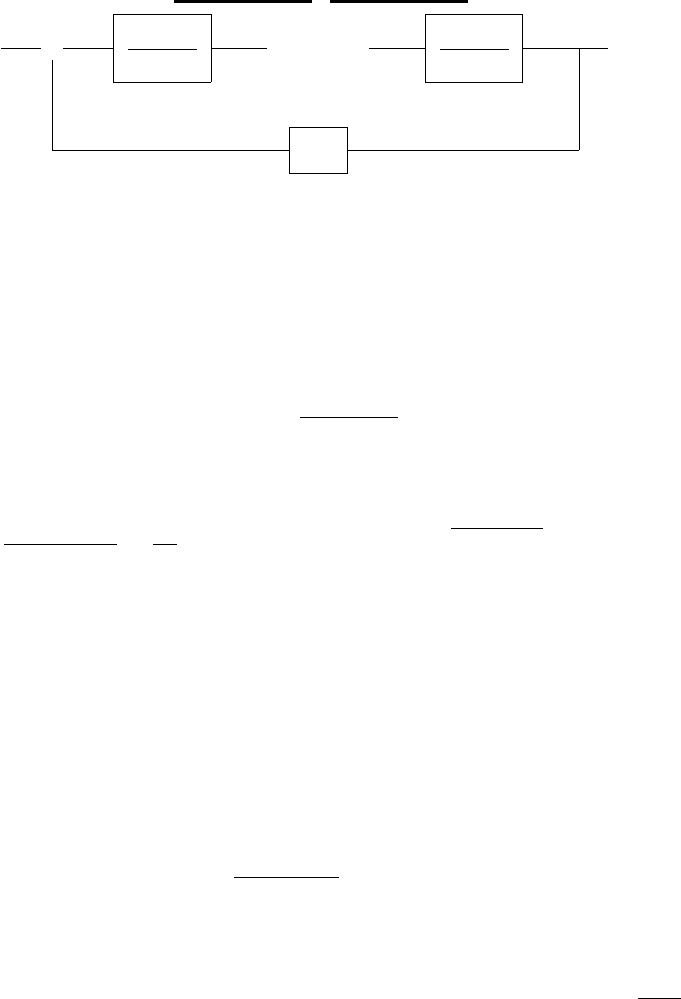
4.1 РЕГУЛЯТОРЫ НИЗКОГО ПОРЯДКА 105

z }| {

1 + T s

. . .

1 + T s

Рис. 4.3: Последовательное соединение звеньев первого порядка с П-регулятором в цепи

обратной связи.

Тогда передаточная функция разомкнутой системы (см. правило (1.16) для после-

довательного соединения) равна

G(s) =

(1 + T s)

Полином B(s) = (1 + T s)

очевидно устойчив (все его корни равны −1/T < 0) и

G(jω) =

(1 + T jω)

, z = 1 + T jω, |z| =

√

1 + T

, ϕ = arctg T ω,

т.е.

G(jω) = (1 + T

)

−n/2

(cos nϕ − j sin nϕ).

Точки пересечения годографа с вещественной осью отвечают значениям ϕ, для которых

sin nϕ = 0, т.е. nϕ = lπ, где l = 0, ±1, . . .. При этом Re G(jω) для таких точек равно

±(1 + T

)

−n/2

. Нас интересуют точки с отрицательной вещественной частью и та из

них, для которой −Re G(jω) максимальна; при n > 2 она соответствует l = 1. Тогда

ϕ = π/n, arctg T ω = π/n, T ω = tg π/n, т.е. κ = −(1 + T

)

−n/2

= −(1 + tg

π/n)

−n/2

−(cos π/n)

. Окончательно получаем значение максимального коэффициента усиления

k =

(cos π/n)

, n > 2. (4.1)

Нетрудно проверить, что при n = 1, 2 замкнутая система устойчива при любом k > 0

(действительно, характеристический полином P (s) = (1+ T s)

+k при n = 1, 2 и любом

k > 0 гурвицев). Например, при n = 3 из формулы (4.1) получаем k =

(0,5)

= 8; это

же следует из критерия устойчивости для кубического полинома P (s) = (1 + T s)

+ k :

> (1 + k)T

, и k < 8.

б. Минимальнофазовый объект. Так называется объект, для которого полином A(s)

устойчив, a

> 0. Как и ранее, характеристический полином равен

P (s) = B(s) + kA(s) = k

A(s) + εB(s)

, ε = 1/k, (4.2)

поэтому P (s) устойчив тогда и только тогда, когда

(s)

= A(s) + εB(s)

106 Глава 4. Стабилизация

устойчив. На первый взгляд ситуация аналогична рассмотренной выше, — A(s) устой-

чив, и можно ожидать, что при 0 ≤ ε < ε сохраняется устойчивость. Однако в дей-

ствительности такой вывод, вообще говоря, не верен. Дело в том, что m — степень

полинома — может быть меньше n — степени , и даже при малых ε > 0 устойчивость

может теряться. Более точный результат учитывает этот эффект. Построим обратный

годограф Найквиста

H(jω) =

B(jω)

A(jω)

, 0 ≤ ω < ∞.

Он всюду определен, так как A(s) устойчив, и потому A(jω) 6= 0 при любом ω. Найдем

∗

из условия:

Im H(jω) = 0, Re H(jω) < 0, Re H(jω) → max

(т.е. найдем корни ω

уравнения Im H(jω) = 0 и среди них найдем тот, для которого

Re H(jω) отрицательно и наиболее близко к 0) и положим ν

= −Re H(jω

∗

) (если такого

∗

нет, ν

= 0).

Теорема 24 Пусть выполнено любое из условий

а). n = m,

б). n = m + 1, b

> 0,

в). n = m + 2, b

> 0, b

n−1

> 0, a

n−1

> a

m−1

Тогда при 0 ≤ ε < ε

= ν (т.е. при k ≥ 1/ν) замкнутая система (4.2) устойчива. В

остальных случаях полином P

(s) неустойчив при малых ε.

Доказательство. При n = m доказательство остается таким же, как и для устойчивого

случая, лишь и меняются ролями.

При n = m + 1 покажем, что полином

(s) = A(s) + εB(s) = a

+ εb

+ . . . + (a

n−1

+ εb

n−1

+ εb

устойчив при малых ε > 0, если b

> 0. В самом деле, понижая степень P

(s) с помощью

Леммы 3, приходим к полиному степени n − 1, коэффициенты которого лишь членами

порядка ε отличаются от коэффициентов A(s), и который, следовательно, устойчив в

силу устойчивости A(s).

Для n = m + 2 имеем

(s) = a

+ εb

+ . . . + (a

n−2

+ εb

n−2

+ εb

n−1

+ εb

Понижая степень P

(s) с помощью Леммы 3, приходим к полиному степени n −1, у ко-

торого старший коэффициент равен εb

n−1

, следующий равен

n−2

+ εb

n−2

−

n−1

n−3

εb

n−3

)

, и оба они по условиям положительны (второй — в силу малости ε). Вновь при-

меняя Лемму 3 и пользуясь алгоритмом Рауса, получаем, что последующие элементы

первого столбца таблицы Рауса для полинома A(s)+εB(s) отличаются от соответствую-

щих элементов таблица Рауса для A(s) лишь членами порядка ε, т.е. положительны для

малых ε в силу устойчивости A(s). Отсюда следует утверждение теоремы в случае в).

Более того, если в случаях б) или в) соответствующие неравенства не выполнены, то

4.1 РЕГУЛЯТОРЫ НИЗКОГО ПОРЯДКА 107

коэффициенты P

(s) имеют разные знаки (например, при n = m + 1, b

≤ 0, старший

коэффициент равен εb

≤ 0, а младший a

+ εb

> 0) и потому P

(s) неустойчив по

критерию Стодолы (см. раздел 3.3).

Наконец, при n > m + 2 полином P

(s) имеет m корней, близких к корням A(s) (и

потому лежащих в левой полуплоскости) и n − m ≥ 3 корней, уходящих в бесконеч-

ность при ε → 0 под равными углами. Такие корни не могут все оставаться в левой

полуплоскости, поэтому при n − m ≥ 3 устойчивости при малых ε не может быть.

Таким образом, в двух случаях можно заведомо стабилизировать систему с помощью

П-регулятора: для устойчивых объектов (с помощью малого коэффициента усиления)

и для минимальнофазовых объектов (с помощью большого коэффициента усиления).

4.1.2 D-разбиение

Стабилизировать объект с помощью П-регулятора можно лишь в редких случа-

ях; как правило, приходится прибегать к помощи регуляторов более сложной струк-

туры. Простейшим из них является пропорционально-интегральный регулятор (ПИ-

регулятор):

C(s) = k

+ k

/s. (4.3)

Иногда рассматривают и другие аналогичные формы регуляторов, например,

C(s) =

s + k

, C(s) =

1 + k

и т.д. Важно, что они зависят лишь от двух параметров k

, k

, поэтому и характери-

стический полином будет зависеть линейно от этих же двух параметров:

P (s, k) = P

(s) + k

(s), k = (k

; k

). (4.4)

Например, для ПИ-регулятора (4.3) будет P

(s) = B(s)s, P

(s) = A(s)s, P

(s) = A(s).

Оказывается, для характеристического полинома вида (4.4) можно указать области на

двумерной плоскости {k

, k

}, в которых он будет обладать заданным количеством

корней в левой и правой полуплоскости (и, в частности, область, отвечающая всем кор-

ням в левой полуплоскости, соответствует устойчивой системе). Этот метод называется

D-разбиением плоскости параметров; его идея заключается в следующем. Пусть при

каком-либо значении k степень полинома P (s, k) равна n, и он имеет m ≤ n корней в ле-

вой полуплоскости и n −m корней — в правой. Как при изменении k может измениться

расположение корней? Ясно, что это может произойти только в одном из следующих

случаев:

а). Изменится степень многочлена P (s, k).

б). Вещественный корень P (s, k) перейдет из одной полуплоскости в другую, т.е.

станет равным 0.

в). Пара комплексных корней перейдет из одной полуплоскости в другую, т.е. P (s, k)

будет иметь пару чисто мнимых корней ±jω.

Таким образом, границы областей D-разбиения описываются параметрическим урав-

нением

P (jω, k) = 0 (4.5)

108 Глава 4. Стабилизация

(соответствующем случаям б) и в)) и уравнением

(k) = 0, (4.6)

где a

(k) — старший коэффициент P (s, k) (случай а)). Уравнение (4.5) при фиксиро-

ванном ω — это два линейных уравнения (отвечающих вещественной и мнимой частям

P (jω, k)) относительно двух переменных k

, k

. В общей ситуации его решение опредeля-

ет одну точку k(ω) на плоскости параметров, при изменении ω от 0 до ∞ она описывает

некоторую кривую. Кроме того, в вырожденном случае (когда линейные уравнения в

(4.5) линейно зависимы) возникают так называемые особые прямые: одному значению ω

отвечает прямая на плоскости параметров. Наконец, условие (4.6) также определяет

прямую линию.

Итак, процедура D-разбиения следующая. Проводится кривая k(ω) (4.5), прямая,

отвечающая условию (4.6) и особые прямые; они разбивают плоскость k на области.

Каждая из этих областей соответствует определенному расположению нулей полинома

P (s, k). Среди этих областей находится и область устойчивости; впрочем она может ока-

заться пустой — тогда характеристический полином неустойчив при любом значении k.

“Расшифровку” расположения нулей в каждой из областей можно делать по-разному.

Например, начать с конкретного полинома P (s, k

) и для него выяснить, сколько его

нулей лежит в левой, а сколько — в правой полуплоскости, а затем из соответствую-

щей ему области переходить к соседним, пользуясь тем, что кривой

(

)

соответствует

переход пары корней через мнимую ось, а особым прямым — переход одного корня че-

рез начало координат. Впрочем, можно в каждой из областей выбрать по точке и найти

корни соответствующих полиномов; то же расположение корней сохраняется и для всех

остальных полиномов из области. Покажем, как эта техника работает на примере.

Пример 4.2 Требуется стабилизировать объект второго порядка

G(s) =

s − 1

+ 1

(он не является ни устойчивым, ни минимальнофазовым) ПИ-регулятором

C(s) = k

Характеристический полином равен

P (s, k) = s(s

+ 1) + (s − 1)(k

s + k

) = s

+ k

+ (1 − k

+ k

)s − k

Его старший коэффициент не зависит от k, поэтому прямая (4.6) отсутствует. Равенство

P (jω, k) = 0 принимает вид

−k

− k

= 0,

ω(1 − k

+ k

− ω

) = 0.

Если ω = 0, то решением является особая прямая

= 0.

4.1 РЕГУЛЯТОРЫ НИЗКОГО ПОРЯДКА 109

При ω 6= 0 точка k(ω) определяется однозначно. При этом нет необходимости находить

эту зависимость, а можно просто исключить ω

= 1−k

из второго уравнения и под-

ставить в первое, тогда уравнение кривой будет задано в явной, а не параметрической

форме:

+ k

(1 − k

+ k

) = 0, k

− k

1 + k

Это уравнение гиперболы, однако условие k

= −ω

< 0 выделяет ее часть, лежащую

во II и IV квадранте, она вместе с прямой k

= 0 осуществляет D-разбиение плоскости

k на 4 области (рис. 4.4).

ﬁgure=c:/sher/book/ﬁgs/4dpart.eps,height=2.5in,width=3in

Рис. 4.4: D-разбиение.

Обозначения D(0), D(1), D(2), D(3) показывают, сколько корней в левой полуплос-

кости y всех полиномов, у которых параметры k лежат в данной области. Небольшая

область D(3) отвечает устойчивым полиномам. Взяв любые значения коэффициентов

ПИ-регулятора внутри этой области, получим устойчивую замкнутую систему.

Для данного примера удалось найти стабилизирующий ПИ-регулятор. Однако в

целом проблема синтеза стабилизирующих регуляторов заданной структуры весьма

сложна; сказать заранее, можно ли данный объект сделать устойчивым с помощью

регулятора низкого порядка, не удается.

4.1.3 Дискретные системы

Рассмотрим, как видоизменяются вышеприведенные методы в случае дискретных

систем. Пусть дискретный объект задан в виде передаточной функции

G(z) =

A(z)

B(z)

где z обозначает оператор сдвига назад, и под устойчивостью полинома понимается

расположение его корней вне едининого круга, |λ

| > 1. Регулятор

C(z) =

N(z)

D(z)

в цепи обратной связи приводит к характеристическому полиному замкнутой системы

P (z) = A(z)N(z) + B(z)D(z);

в частности, при C(z) = k имеем

P (z)

= P

(z) = kA(z) + B(z).

Теоремы 23 и 24 приобретают следующий вид.

110 Глава 4. Стабилизация

Теорема 25 Если объект G(z) устойчив (т.е. полином B(z) устойчив), то при 0 ≤

k ≤ k полином P

(z) устойчив. Если объект G(z) минимальнофазовый (т.е. полином

A(z) устойчив), то при k ≥ k полином P

(z) устойчив. При этом

k = min

−1/G(e

jω

) : Im G(e

jω

) = 0, Re G(e

jω

) < 0

в первом случае и

k = max

−1/G(e

jω

) : Im G(e

jω

) = 0, Re G(e

jω

) < 0

во втором случае.

Таким образом, аргумент jω в непрерывном случае заменяется на e

jω

в дискретном;

с этим мы уже встречались и раньше (Гл. 3). Более существенно, что в Теореме 25, в

отличие от ее непрерывных аналогов, нет никаких требований к степеням полиномов A

и B. Дело в том, что в дискретном случае у полинома

= A + εB, deg A = m, deg B = n > m,

при малом ε любого знака m корней близки к корням A, а n − m корней “приходят

из бесконечности” (т.е. велики по модулю). Поэтому если A — устойчивый полином,

то и P

будет устойчивым при малых ε (именно здесь мы пользуемся определением

устойчивости полиномов в форме |λ

| > 1 — “приходящие из бесконечности” корни

являются устойчивыми). В остальном доказательство Теоремы 25 проводится так же,

как и в непрерывном случае. Дискретное D-разбиение осуществляется так же, как и

для непрерывных полиномов, с заменой аргумента jω на e

jω

Сопутствующие функции Matlab:

tf (CST) — задание системы с помощью передаточной функции;

rlocus (CST) — построение корневых годографов;

nyquist (CST) — построение годографа Найквиста.

4.2 Общий вид стабилизирующих регуляторов

В разделе 4.1 отмечалось, что проблема стабилизации регулятором заданной струк-

туры не всегда имеет решение и достаточно сложна. Ситуация иная, если не ограничи-

вать порядок регуляторов. Именно, в предположении управляемости системы проблема

стабилизации всегда имеет решение, и все стабилизирующие регуляторы имеют простое

описание. Ниже мы займемся этим кругом вопросов.

Пусть одномерный объект задан с помощью передаточной функции

G(s) =

A(s)

B(s)