Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление

Подождите немного. Документ загружается.

7.1. Робастная устойчивость полиномов 171

Теорема 44 (Харитонов) Для робастной устойчивости интервального семейства

(7.3) необходимо и достаточно, чтобы все полиномы Харитонова были устойчивы.

Доказательство. Необходимость устойчивости полиномов Харитонова тривиальна,

так как они входят в интервальное семейство. Чтобы доказать достаточность, восполь-

зуемся Теоремой 43 и построим множество S(ω). Представим

P (jω)

= U(ω) + jωV (ω),

U(ω) = a

− a

+ a

− . . . ; V (ω) = a

− a

+ a

− . . .

Ясно, что

U(ω) ≤ U(ω) ≤ U(ω), V (ω) ≤ V (ω) ≤ V (ω),

где

U(ω) = a

− a

+ a

− . . . , U(ω) = a

− a

+ a

− . . . ,

V (ω) = a

− a

+ a

− . . . , V (ω) = a

− a

+ a

− . . .

Иначе говоря, P (jω) может изменяться в прямоугольнике, вершинами которого явля-

ются точки

= U(ω) + jωV (ω), z

= U(ω) + jωV (ω),

= U(ω) + jωV (ω), z

= U(ω) + jωV (ω).

Нетрудно видеть, что z

= P

(jω), i = 1, . . . , 4, т.е. S(ω) — прямоугольник, вершины ко-

торого соответствуют харитоновским полиномам. Покажем, что S(ω) не содержит на-

чала координат при любом 0 ≤ ω < ∞. Действительно, при ω = 0 имеем 0 /∈ S(0) (иначе

было бы P (0) = a

= 0, что противоречит условию a

> 0), поэтому если 0 ∈ S(ω

) при

каком-то ω

> 0, то должно произойти пересечение границы прямоугольника S(ω) с

началом координат при некотором 0 < ω

≤ ω

. Это пересечение не может произойти

ни в какой вершине прямоугольника S(ω), так как вершины соответствуют устойчивым

харитоновским полиномам. Пусть это пересечение произойдет с некоторым ребром, на-

пример в точке z = λz

+ (1 − λz

), 0 < λ < 1. Поскольку P

(s) и P

(s) устойчивы, то

в силу критерия Михайлова (Теорема 9) аргументы P

(jω) и P

(jω) монотонно строго

возрастают с ростом ω, однако это противоречит тому, что сторона z

прямоугольника

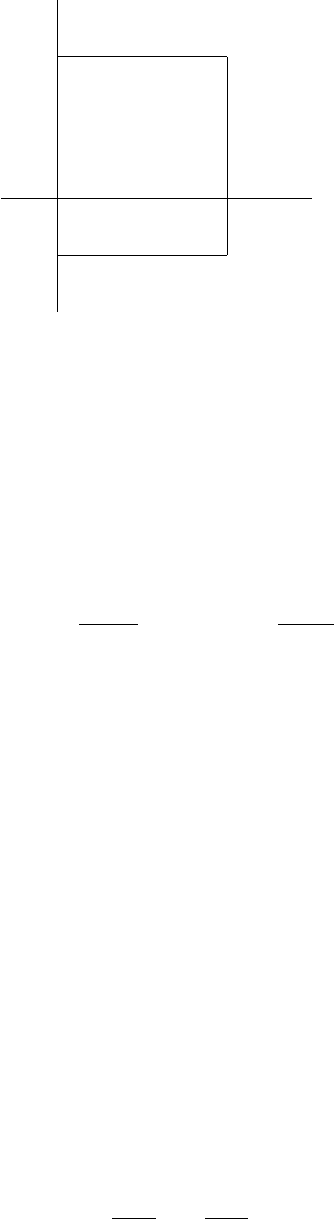
S(ω) остается вертикальной (см. рис. 7.1).

Таким образом, выполнены все условия Теоремы 43 , т.е. из устойчивости харито-

новских полиномов следует робастная устойчивость интервального семейства.

Теореме Харитонова можно придать графическую форму. При этом достаточно про-

верять поведение лишь одного (а не четырех) годографов, и, кроме того, одновременно

можно найти максимальный размах неопределенности, при котором сохраняется ро-

бастная устойчивость. С этой целью запишем интервальное семейство в форме (6.7):

P(s) =

P (s) = a

+ a

s + . . . + a

, |a

− a

| ≤ γα

, i = 0, 1, . . . , n

, (7.4)

причем считаем α

, α

> 0, и введем следующие величины:

(jω)

= U

(ω) + jωV

(ω);

172 Глава 7. Робастная устойчивость

u u

S(ω

)

(ω

)

(ω), ω > ω

©¼

(ω

)

(ω),

ω > ω

(ω

)

(ω

)

Рис. 7.1: Движение области значений S(ω).

(ω)

= a

− a

+ a

− . . . , V

(ω)

= a

− a

+ a

− . . . ;

R(ω)

= α

+ α

+ . . . , T (ω)

= α

+ α

+ . . . .

Построим годограф

z(ω) = x(ω) + jy(ω), 0 ≤ ω ≤ ∞,

x(ω) =

(ω)

R(ω)

, y(ω) =

(ω)

T (ω)

(7.5)

который часто называется годографом Цыпкина-Поляка.

Теорема 45 (графический критерий) Для робастной устойчивости семейства (7.4)

необходимо и достаточно, чтобы

> γα

, a

> γα

, (7.6)

и годограф z(ω) при изменении ω от 0 до ∞ проходил последовательно через n квад-

рантов против часовой стрелки и не пересекал квадрата с вершинами (±γ, ±γ).

Доказательство. Очевидно, что область значений семейства (7.4) — это прямоуголь-

ник

S(ω) =

z = x + jy : |x − U

(ω)| ≤ γR(ω), |y −ωV

(ω)| ≤ γωT (ω)

а условие 0 /∈ S(ω) эквивалентно тому, что |U

(ω)| ≤ γR(ω), |V

(ω)| ≤ γT (ω), т.е.

|x(ω)| ≤ γ, |y(ω)| ≤ γ. Поэтому непересечение годографа z(ω) с квадратом {z = x + jy :

|x| ≤ γ, |y| ≤ γ} эквивалентно условию 0 /∈ S(ω). Далее, по критерию Михайлова поли-

ном P

(s) устойчив тогда и только тогда, когда годограф P

(jω) проходит последова-

тельно через n квадрантов, но P

(jω) = U

(ω) + jωV

(ω) лежит в каком-либо квадранте

тогда и только тогда, когда z(ω) =

(ω)

R(ω)

+ j

(ω)

T (ω)

лежит в том же квадранте. Итак,

z(ω) проходит через n квадрантов тогда и только тогда, когда P

(s) устойчив. Наконец,

условие (7.6) требуется для обеспечения положительности коэффициентов a

и a

для

всех полиномов семейства. Тем самым Теорема 45 эквивалентна принципу исключения

нуля (Теорема 43) для данного семейства.

7.1. Робастная устойчивость полиномов 173

Таким образом, построив годограф z(ω), можно не только проверить робастную

устойчивость при фиксированном γ > 0, но и найти наибольшее γ = γ

max

, для которого

робастная устойчивость сохраняется при всех γ < γ

max

. Такое γ

max

называется радиусом

устойчивости интервального семейства; оно находится по формуле

max

= min{γ

∗

, γ

∞

}, (7.7)

где γ

∗

— размер наибольшего квадрата {|x| ≤ γ

∗

, |y| ≤ γ

∗

}, вписанного в годограф

z(ω), γ

= a

/α

, а γ

∞

= a

/α

Пример. Задан номинальный полином 6-ой степени с коэффициентами

= (433, 5 667, 25 502, 72 251, 25 80, 25 14 1)

и размахами коэффициентов

α = (43, 35 33, 36 25, 137 15, 075 5, 6175 1, 4 0, 1).

На рис. 7.2 показан вид годографа z(ω) и вписанный в него наибольший квадрат; из

него находим γ

max

≈ 1, 2372.

ﬁgure=c:/sher/book/ﬁgs/7tspol.eps,height=2.5in,width=3in

Рис. 7.2: Годограф Цыпкина-Поляка.

Отметим, что годограф (7.5) существенно отличается от годографа Михайлова —

он начинается внутри первого квадранта, а не на вещественной оси, и заканчивается в

конечной точке z(∞), а не уходит на бесконечность (поскольку дробно-рациональные

функции x(ω), y(ω) имеют одинаковые степени числителя и знаменателя).

Для семейств (7.3), (7.4) неопределенными параметрами являются сами коэффици-

енты полиномов. Перейдем теперь к изучению более сложной ситуации — аффинному

семейству полиномов:

P(s, Q) = {P

(s) + q

(s) + . . . + q

(s), |q

| ≤ γ, i = 1, . . . , `}, (7.8)

с параметрами, изменяющимися в кубе

= {q ∈ R

: |q|

∞

≤ γ}. (7.9)

Одномерное семейство вида

P (s, q): |q

| = γ, i 6= k, |q

| ≤ γ

назовем реберным полиномом. Напомним (см. раздел 6.1), что вершинными полинома-

ми мы назвали полиномы вида P (s, q), q

= ±γ, i = 1, . . . , `. Геометрически вершинные

и реберные полиномы соответствуют вершинам и ребрам куба (7.9), т.е. реберный по-

лином “соединяет” два “соседних” вершинных полинома (соответствующих соседним

вершинам куба), и всего имеется ` 2

`−1

реберных полиномов. Справедлива следующая

174 Глава 7. Робастная устойчивость

Теорема 46 (реберная теорема) Пусть

deg P

≤ deg P

= n, i = 1, . . . , `, (7.10)

i=1

| < |a

|, γ

i=1

| < |a

|, (7.11)

где a

, i = 1, . . . , `, — коэффициенты при s

полиномов P

(s). Пусть полином P

(s)

устойчив. Тогда для робастной устойчивости семейства (7.8) необходима и доста-

точна устойчивость всех реберных полиномов.

Доказательство. Мы воспользуемся Теоремой 43 с q

= 0; тогда неравенства (7.10)–

(7.11) гарантируют условие a

(q) 6= 0, q ∈ Q, для старшего коэффициента полинома

P (s, q) (7.8). Нам остается проверить принцип исключения нуля (7.2). Область S(ω)

имеет вид

S(ω) =

z ∈ C : z = P

(jω) +

i=1

(jω), |q|

∞

≤ γ

т.е. это аффинный двумерный образ `-мерного куба. Такой образ является многоуголь-

ником, стороны которого — образы ребер куба Q. Поскольку 0 /∈ S(0) (в силу (7.11)), то

может оказаться 0 ∈ S(ω), лишь если 0 будет принадлежать границе S(ω) для некоторо-

го ω > 0. Однако это невозможно, так как граница соответствует реберным полиномам,

а они по предположению устойчивы.

Реберная теорема позволяет получить эффективную формулировку критерия ро-

бастной устойчивости, лишь если число ` неопределенных параметров мало. В этом

случае следует проверить все реберные полиномы. Они представляют собой однопа-

раметрические семейства вида λM(s) + (1 − λ)N(s) (где M(s), N(s) — два соседних

вершинных полинома), и в соответствии с критерием Найквиста (роль точки −1 здесь

играет −(1 − λ)/λ) их устойчивость при 0 ≤ λ ≤ 1 эквивалентна тому, что полиномы

M(s), N(s) устойчивы, а годограф G(jω) = M(jω)/N(jω) не пересекает отрицательной

вещественной полуоси. Однако, если ` велико, то число таких проверок значительно

(даже для ` = 5 нужно проверить ` 2

`−1

= 80 реберных полиномов). Можно предло-

жить другой способ, основанный на более конструктивном описании множества S(ω);

мы используем этот подход позже, при исследовании робастной устойчивости дискрет-

ных полиномов.

До сих пор мы рассматривали семейства с линейно входящими неопределенными

параметрами, которые изменялись независимо в кубе (параллелепипеде). Перейдем те-

перь к анализу сферических семейств. Проверку робастной устойчивости и определение

радиуса устойчивости также можно осуществить с помощью графических критериев

типа Теоремы 45. Рассмотрим эллиптические ограничения (6.5):

P(s) =

P (s) = a

+ a

s + . . . + a

i=0

− a

)

≤ γ

, (7.12)

где, как и раньше, a

— коэффициенты номинального полинома P

(s), α

≥ 0 — масшта-

бы изменения коэффициентов a

(при α

≡ 1 ограничения переходят в сферические),

7.1. Робастная устойчивость полиномов 175

причем α

, α

> 0, а γ > 0 — общий размах неопределенности. Как и в Теореме 45,

введем следующие величины:

(jω)

= U

(ω) + jωV

(ω);

(ω)

= a

− a

+ a

− . . . , V

(ω)

= a

− a

+ a

− . . . ;

R(ω)

= (α

+ α

+ . . .)

1/2

, T (ω)

= (α

+ α

+ . . .)

1/2

;

и построим годограф

z(ω) = x(ω) + jy(ω), 0 ≤ ω ≤ ∞,

x(ω) =

(ω)

R(ω)

, y(ω) =

(ω)

T (ω)

(7.13)

Теорема 47 Для робастной устойчивости семейства (7.12) необходимо и достаточ-

но, чтобы a

> γα

, a

> γα

, и годограф z(ω) при изменении ω от 0 до ∞ проходил

последовательно через n квадрантов против часовой стрелки и не пересекал круга

радиуса γ с центром в нуле.

Доказательство в точности повторяет рассуждения Теоремы 45 (т.е. основано на

принципе исключения нуля), с той лишь разницей, что область значений S(ω) — эллипс

S(ω) =

(z −P

(jω))

−1

(z −P

(jω)) ≤ γ

где

M = M(ω) = A(ω)A

(ω), A(ω) =

0 −α

0 α

0 . . .

0 α

ω 0 −α

0 α

. . .

Таким образом, радиус устойчивости эллиптического семейства (7.12) вычисляется

следующим образом:

max

= min{γ

∗

, γ

∞

где γ

∗

— радиус наибольшего круга, вписанного в годограф z(ω), γ

= a

/α

, γ

∞

/α

Для того же семейства 6-й степени из рассмотренного выше примера получаем

max

≈ 2, 8380, т.е. больше, чем величина радиуса устойчивости (7.7) соответствующего

интервального полинома, что неудивительно, так как ограничения на неопределенность

в семействе (7.12) более жесткие, чем в семействе (7.4): эллипсоид {a = (a

, . . . , a

)

i=0

− a

)

/α

≤ γ

} содержится в параллелепипеде {a = (a

, . . . , a

)

: |a

− a

| ≤

γα

, i = 0, 1, . . . , n}.

Отметим, что для сферических семейств не существует аналогов теоремы Харитоно-

ва: робастная устойчивость семейства не определяется устойчивостью конечного числа

элементов семейства.

Остановимся кратко на задаче о робастной устойчивости полинома, мультилинейно

зависящего от параметров, например (6.10):

P (s, T, k) = (1 + T

s) · . . . · (1 + T

s) + k

· . . . · k

176 Глава 7. Робастная устойчивость

при

T, k ∈ R

: T

≤ T

, k

≤ k

Эта задача существенно более сложна, чем рассмотренные выше. Так, область S(ω)

оказывается, вообще говоря, невыпуклой; ее границы порождены не только ребрами Q и

являются криволинейными. В некоторых частных случаях, однако, задача значительно

упрощается. Например, если интервалы неопределенности для T

не перекрываются:

< T

< . . . < T

< T

(порядок следования интервалов может быть любым), то S(ω) — многоугольник с 2`

ребрами, допускающими явное описание. Поэтому задача робастной устойчивости в

этой ситуации может быть эффективно разрешена.

В заключение рассмотрим проблему робастной устойчивости дискретных полино-

мов. Семейство полиномов

P(z, Q)

P (z, q) = a

(q) + a

(q)z + . . . + a

(q)z

, q ∈ Q

(7.14)

робастно устойчиво, если для всех значений параметра q ∈ Q ⊂ R

полиномы P (z, q)

дискретно устойчивы, т.е.

(q)| > 1, i = 1, . . . , n, q ∈ Q,

где z

(q) — корни P (z, q). Принцип исключения нуля принимает следующий вид.

Теорема 48 Пусть P (z, q

) устойчив для некоторого q

∈ Q и Q связно, тогда усло-

вие

0 /∈ S(ω)

P (e

jω

, q): q ∈ Q

, ∀ 0 ≤ ω < 2π

необходимо и достаточно для робастной устойчивости семейства (7.14).

Доказательство проводится точно так же, как в Теореме 43, и мы его опускаем. Раз-

ница лишь в том, что границей между устойчивыми и неустойчивыми корнями в непре-

рывном случае являлась мнимая ось jω, а в дискретном случае — это окружность e

jω

0 ≤ ω < 2π. Отметим также некоторое различие в формулировках теорем — в дискрет-

ном случае не требуется, чтобы все полиномы P (z, q) имели одинаковую степень (от-

сутствует условие a

(q) 6= 0). Это связано с тем, что полином вида P

(z) = P

(z) +εz

n+1

(где P

(z) — устойчивый полином степени n) устойчив при малых ε (см. раздел 4.1.3).

Для эффективного использования Теоремы 48 нужно уметь строить область значе-

ний S(ω). Начнем с интервального семейства

P (z) = a

+ a

z + . . . + a

, |a

− a

| ≤ γα

, α

> 0, i = 0, . . . , n. (7.15)

Для непрерывного случая область S(ω) была прямоугольником. В дискретном слу-

чае

S(ω) =

jω

) + γ

k=0

jωk

= c

k=0

7.1. Робастная устойчивость полиномов 177

где c

= P

jω

), z

= γα

jωk

, а µ

— произвольные числа, изменяющиеся от −1 до +1.

Отсюда следует, что S(ω) — многоугольник с центром в c

и сторонами, параллельны-

ми z

, k = 0, . . . , n; всего у этого многоугольника 2n + 2 ребер и столько же вершин.

Исключением являются значения ω = 0 и ω = π, для которых S(ω) — отрезок. Условие

0 /∈ S(ω) можно записать в аналитической форме, оно эквивалентно условиям

γ < γ(ω)

= max

i=0

cos(i − k)ω

i=0

|cos(i − k)ω|

, ω 6= 0, π;

γ < γ(0) =

i=0

;

γ < γ(π) =

i=0

(−1)

i=0

Таким образом, радиус устойчивости (в предположении устойчивости полинома P

(z))

вычисляется так:

max

= min

0≤ω<2π

γ(ω).

Эти формулы отличаются от тех, которые были получены для непрерывного случая (7.7).

Более того, в дискретном случае нет никакого аналога теоремы Харитонова — устойчи-

вость даже всех вершинных полиномов не гарантирует робастной устойчивости интер-

вального семейства (7.15). Дело, как уже отмечалось, заключается в различии геомет-

рии области значений S(ω) — в непрерывном случае это прямоугольник с заданными

направлениями сторон, тогда как в дискретном это многоугольник с 2n + 2 вершинами

и меняющимися направлениями сторон.

Для аффинного семейства дискретных полиномов верна реберная теорема; впро-

чем, радиус уcтойчивости для такого семейства можно вычислять и иначе, используя

представление области S(ω) в виде многоугольника, подобно тому как это было сделано

выше для интервального семейства.

Отметим другое семейство дискретных полиномов, для которых область S(ω) имеет

простой вид. Именно, рассмотрим

P(z)

P (z) = a

+ a

z + . . . + a

k=0

− a

| ≤ γ, n = 0, 1, . . .

. (7.16)

В этом семействе отклонения коэффициентов ограничены в l

-норме, а степень полино-

мов P (z) не ограничена. Оказывается, для всех ω таких, что ω/π иррационально (т.е.

для почти всех ω) замыкание множества S(ω) — круг радиуса γ с центром в P

jω

Отсюда следует выражение для радиуса устойчивости этого семейства:

max

= min

0≤ω<2π

¯P

jω

)

¯.

178 Глава 7. Робастная устойчивость

Здесь P

(z) — аналитическая функция в круге |z| ≤ 1,

(z) = a

+ a

z + . . . + a

+ . . . ,

∞

k=0

| < ∞, и P

(z) 6= 0, при |z| ≤ 1.

Мы видим, что различные структуры неопределенности и различные виды огра-

ничений на неопределенные параметры приводят к большому разнообразию форм об-

ластей значений; тем не менее многие задачи могут решаться единообразно на основе

принципа исключения нуля и применения графических критериев устойчивости типа

критерия Михайлова.

7.2 Робастная устойчивость матриц

Обратимся теперь к параметрическим семействам матриц, таким как интервальное

семейство, задаваемое в форме

A = ((a

)), a

≤ a

, i, j = 1, . . . , n, (7.17)

или

A = A

+ ∆, ∆ = ((∆

)), |∆

| ≤ γ, i, j = 1 , . . . , n, (7.18)

либо аффинное семейство

A(q) = A

i=1

, |q

| ≤ γ, i = 1, . . . , `. (7.19)

Семейство называется робастно устойчивым, если устойчивы все его элементы, т.е.

Re λ

< 0, i = 1, . . . , n,

при всех q (∆ для семейства (7.18)) из допустимого множества, где λ

— собственные

значения A. При этом, как и для семейств полиномов, наибольшее γ = γ

max

, для ко-

торого робастная устойчивость сохраняется при всех γ < γ

max

называется радиусом

устойчивости матричного семейства.

Можно было бы ожидать, что проблемы робастной устойчивости таких матричных

семейств решаются приблизительно так же, как и для соответствующих семейств поли-

номов. Однако оказывается, что ситуация с матрицами значительно более сложная. Так,

для интервального семейства (7.17) нет никакого аналога теоремы Харитонова (все вер-

шинные матрицы могут быть устойчивы, однако робастная устойчивость отсутствует),

для аффинного семейства (7.19) неверна реберная теорема и т.д. Формальное пояснение

этого заключается в том, что в характеристический полином P (s, q) = det

sI − A(q)

параметры q входят нелинейно (мультилинейно для интервального семейства (7.17) и

полиномиально для аффинного семейства (7.19)), поэтому применить реберную теоре-

му или какой-либо иной результат предыдущего параграфа мы не можем. В связи с

этим обсудим совсем иные подходы к проблеме.

7.2. Робастная устойчивость матриц 179

Первый из них основан на идеях теории возмущений. Пусть нам известны соб-

ственные числа λ

(0) и собственные векторы e

(0) матрицы A(0). Как они изменятся

при малом возмущении A(q) этой матрицы? Здесь q ∈ R

— векторный параметр, при-

чем матрица A(q) зависит от этого параметра дифференцируемым образом, так что

существуют и известны матрицы D

∂A(q)

∂q

q=0

. Например, для семейства (7.19) имеем

A(0) = A

, D

= A

. Ответ дается следующей основной теоремой теории возмущений,

(см. также разделы 10.3 и 10.2 Приложения).

Теорема 49 Пусть все собственные значения λ

(0) матрицы A(0) различны, а x

— соответствующие им правые и левые собственные векторы:

A(0)x

= λ

(0)x

, y

∗

A(0) = λ

(0)y

∗

, |x

| = |y

| = 1, k = 1, . . . , n.

Тогда собственные значения матрицы A(q) имеют вид

(q) = λ

(0) +

i=1

∗

+ o(q).

Этот результат дает возможность оценить, насколько чувствительны собственные

числа матрицы A(q) к изменению параметра q. Пусть, например, матрица A(0) устой-

чива, а λ — ее собственное значение, имеющее наибольшую вещественную часть. Если x

и y — соответствующие правый и левый собственные векторы, а семейство матриц аф-

финное (7.19), то для матрицы A(q) это собственное значение переходит в

λ(q) ≈ λ +

i=1

∗

для малых q, поэтому Re λ(q) ≈ Re λ+

i=1

, где α

= Re

∗

, и max Re λ(q) по |q

| ≤

γ, i = 1, . . . , `, достигается при q

= γ sign α

и равен приближенно Re λ + γ

i=1

|α

Итак, можно ожидать, что при γ

∗

= −

Re λ

i=1

|α

матрица A(q) потеряет устойчивость

(Re λ(q) станет равным нулю), т.е. γ

∗

— оценка радиуса устойчивости для A(q). Ра-

зумеется, этот анализ лишь приближенный, и никаких гарантированных выводов о

робастной устойчивости семейства (7.19) при фиксированном γ на этом пути получить

нельзя.

Другой подход связан с использованием достаточных условий робастной устойчи-

вости. Можно потребовать, чтобы у всего семейства матриц A(q), q ∈ Q была общая

функция Ляпунова V (x) = x

P x, P > 0. Мы знаем (см. Приложение, раздел 9.1), что

существование решения матричного неравенства A

P + P A < 0, P > 0, гарантирует

устойчивость матрицы A; тем самым существование решения системы линейных мат-

ричных неравенств

(q)P + P A(q) < 0, P > 0, q ∈ Q, (7.20)

гарантирует робастную устойчивость матричного семейства A(q). Если A(q) — семей-

ство интервальных матриц (7.17) или аффинное семейство (7.19), то неравенства (7.20)

180 Глава 7. Робастная устойчивость

достаточно решить лишь для вершин множества Q (обозначим их через V ); поскольку

любая точка q ∈ Q представляется как выпуклая комбинация вершин, то из выполне-

ния (7.20) для вершин будет следовать, что (7.20) удовлетворяется (с данным P ) и для

любого q ∈ Q. Итак, достаточно решить конечное число матричных неравенств

)P + P A(q

) < 0, P > 0, q

∈ V, (7.21)

где A(q

) — вершинные матрицы: в случае семейства (7.17) это те матрицы, в которых

все a

принимают крайние значения (либо a

, либо a

), а в случае семейства (7.19)

это матрицы, для которых |q

| = γ, i = 1, . . . , `. Ясно, что число неравенств в (7.21)

достаточно велико даже если n и ` не слишком большие числа. Впрочем, существуют

простые итеративные методы решения неравенств (7.21), работоспособные даже для

больших размерностей.

В то же время нужно ясно понимать, что мы получили лишь достаточный критерий

робастной устойчивости. Если система линейных матричных неравенств (7.20) не имеет

решения, то это не значит, что робастная устойчивость нарушена — могут существо-

вать робастно устойчивые семейства, для которых нет общей квадратичной функции

Ляпунова.

Другое достаточное условие заключается в использовании сверхустойчивости вме-

сто устойчивости. Покажем как такой подход работает на примере интервального мат-

ричного семейства, записанного в виде (6.9):

A = ((a

)), a

= a

+ ∆

, |∆

| ≤ γm

, i, j = 1 . . . , n, (7.22)

где номинальная матрица A

= ((a

)) сверхустойчива, т.е.

σ(A

)

= min

−a

−

j6=i

> 0.

Потребуем, чтобы условие сверхустойчивости сохранялось для всех матриц семейства:

−(a

+ ∆

) −

j6=i

+ ∆

| > 0, i = 1, . . . , n.

Ясно, что это неравенство будет выполнено для всех допустимых ∆

тогда и только

тогда, когда

−a

− γm

−

j6=i

| + γm

> 0, i = 1, . . . , n.

т.е. при

γ < γ

∗

= min

−a

−

j6=i

В частности, если m

≡ 1 (масштабы изменения всех элементов матрицы одинаковы),

то

∗

σ(A

)