Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление

Подождите немного. Документ загружается.

7.6. Выводы 201

при этом радиус сверхустойчивости γ

∗

находится в явном виде. Аналогичные

формулы справедливы и в дискретном случае: если kA

< 1, то семейство мат-

риц остается сверхустойчивым при

γ < γ

∗

1 − kA

• При задании матричной неопределенности в виде ограничений на спектральную

норму возмущения

A = A

+ ∆, k∆k ≤ γ

нахождение радиуса устойчивости — максимального значения γ = γ

max

, при ко-

тором все возмущения k∆k < γ

max

не нарушают устойчивости A

, — зависит от

типа возмущений.

Если возмущения ∆ комплексные, то выражение для комплексного радиуса устой-

чивости γ

max

= γ

max

дается Теоремой 50. При этом дестабилизирующее возмуще-

ние при γ ≥ γ

max

может быть взято в виде матрицы ранга один.

Если допускать лишь вещественные возмущения ∆, то нахождение вещественно-

го радиуса устойчивости γ

max

= γ

max

усложняется; выражение для γ

max

дается

Теоремой 52. Дестабилизирующими возмущениями являются матрицы второго

ранга.

Аналогичные результаты справедливы для дискретных систем, т.е. матриц, устой-

чивых по Шуру.

• Для одномерных систем с частотной неопределенностью вопрос о робастной устой-

чивости решается с помощью робастного аналога критерия Найквиста (Теоре-

ма 55).

Для многомерных систем основным техническим аппаратом исследования устой-

чивости при частотной неопределенности является теорема о малом коэффициен-

те усиления. Пусть M(s) — матричная передаточная функция из RH

∞

, ∆(s) —

матричное частотное возмущение из RH

∞

, ограниченное в H

∞

-норме: k∆(s)k

∞

≤

1/γ. Тогда матричная функция

I +M(s)∆(s)

−1

определена и принадлежит RH

∞

тогда и только тогда, когда kM(s)k

∞

≤ γ (Теорема 56). Отсюда можно получить

разнообразные критерии робастной устойчивости при частотной неопределенно-

сти. Типичные результаты приведены в Теореме 57. Пусть объект имеет адди-

тивную неопределенность: G = G

+ W

∆W

, а регулятор C(s) помещен в цепи

обратной связи. Тогда замкнутая система устойчива при всех k∆(s)k

∞

≤ 1, если

CSW

∞

< 1, где S = (I +G

−1

— чувствительность номинального объекта.

• Общая схема исследования робастной устойчивости дается так называемым µ-

анализом. Он основан на понятии структурного сингулярного числа матрицы. В

µ-анализе система приводится к стандартной M–∆ конфигурации, где все неопре-

деленности ∆ включены в цепь искусственной обратной связи, а M — номиналь-

ная замкнутая система (включающая номинальный объект, регулятор и обратную

202 Глава 7. Робастная устойчивость

связь). Матричная неопределенность ∆(s) имеет некоторую структуру (в ней мо-

гут быть блоки, отвечающие вещественной или комплексной параметрической или

матричной неопределенности, частотной неопределенности). Число µ(M) опреде-

ляется как обратное к минимальной норме ∆ заданной структуры, при которой

матрица I + M∆ становится вырожденной. Для вычисления µ(M) существуют

численные методы, основанные на верхних и нижних границах для µ(M). Общий

критерий робастной устойчивости для M–∆ конфигурации дается Теоремой 59,

обобщающей теорему о малом коэффициенте усиления.

• Теория робастной устойчивости опирается на минимаксный подход — требуется

сохранение устойчивости при любой допустимой неопределенности. Однако мож-

но считать неопределенность случайной, а систему робастно устойчивой, если она

сохраняет устойчивость с вероятностью, близкой к единице. Такой вероятност-

ный подход имеет ряд преимуществ. В частности, можно применить метод Монте-

Карло для прямой проверки вероятностной устойчивости. Вероятностный радиус

устойчивости часто оказывается заметно б´льшим, чем детерминированный.

Глава 8

Робастная стабилизация и управление

В этой главе мы проанализируем каким образом методы стабилизации и оптималь-

ного управления, рассмотренные в Главах 4 и 5, могут быть обобщены на задачи с

неопределенностями различных видов. Разумеется, не все описанные там методы до-

пускают “робастизацию”. Например, подход с помощью размещения полюсов системы

(раздел 4.3) имеет смысл только для фиксированной системы. С другой стороны, воз-

можны и специальные постановки задач, связанные с робастностью, например, задача

о максимальной робастности (раздел 8.4).

8.1 Робастная стабилизация с помощью регуляторов

низкого порядка

Как и в разделе 4.1, мы займемся вначале задачей стабилизации одномерного объ-

екта с передаточной функцией

G(s) =

A(s)

B(s)

с помощью скалярного коэффициента усиления k в цепи обратной связи.

G(s)

Рис. 8.1: Стабилизация неопределенного объекта скалярной обратной связью.

Однако, здесь, в отличие от раздела 4.1, G(s) не предполагается фиксированной,

а содержит некоторую неопределенность. Для примера будем считать, что A и B —

интервальные полиномы:

A(s) = a

+ a

s + . . . + a

, a

≤ a

, i = 1, . . . , m;

B(s) = b

+ b

s + . . . + b

, b

≤ b

, i = 1, . . . , n.

203

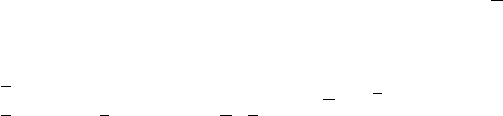
204 Глава 8. Робастная стабилизация и управление

Характеристический полином замкнутой системы

P (s) = B(s) + kA(s)

при фиксированном коэффициенте усиления k также будет интервальным полиномом

с коэффициентами p

= b

+ ka

, i = 1, . . . , n (мы предполагаем, что n ≥ m и дополняем

= 0 для m < i ≤ n). По теореме Харитонова 44 P (s) устойчив в том и только в том

случае, когда устойчивы четыре харитоновских полинома

(s) = B

(s) + kA

(s), i = 1, . . . , 4,

где A

(s), B

(s) — харитоновские полиномы для интервальных семейств A(s), B(s) (см.

раздел 7.1). Используя Теоремы 23 и 24 о стабилизации устойчивых и минимальнофа-

зовых объектов, получаем их робастные аналоги.

Теорема 61 Пусть полиномы B

(s), i = 1, . . . , 4, устойчивы. Тогда система на рис. 8.1

робастно стабилизируется при 0 ≤ k < k

= min

1≤i≤4

, где k

= −1/κ

, а κ

— точка

самого левого пересечения i-го годографа Найквиста G

(jω) = A

(jω)/B

(jω) с отрица-

тельной вещественной полуосью.

Теорема 62 Пусть полиномы A

(s), i = 1, . . . , 4, устойчивы, a

> 0, и выполнено

любое из условий

а). n = m,

б). n = m + 1, b

> 0,

в). n = m + 2, b

> 0, b

n−1

> 0, a

n−1

> a

m−1

Тогда система на рис. 8.1 робастно стабилизируется при k > k

= max

1≤i≤4

, где k

−1/ν

, а ν

— точка самого левого пересечения i-го обратного годографа Найквиста

(jω) = B

(jω)/A

(jω) с отрицательной вещественной полуосью.

Таким образом, робастно устойчивые и робастно минимальнофазовые объекты мож-

но робастно стабилизировать с помощью постоянной обратной связи (в первом случае

с помощью малого, а во втором случае — большого коэффициента усиления). При этом

для отыскания критического значения коэффициента усиления k достаточно постро-

ить четыре харитоновских годографа, соответствующих либо прямым, либо обратным

годографам Найквиста.

Сходным образом допускает робастное обобщение и техника, основанная на D-раз-

биении по двум параметрам, описанная в разделе 4.1. Как мы видели, для регуляторов,

зависящих от двух параметров k

, k

, характеристический полином принимает вид (4.4):

P (s, k) = P

(s) + k

(s), k = (k

, k

где полиномы P

(s), P

(s) линейно зависят от A(s) и B(s). Например, для ПИ-

регулятора

C(s) = k

+ k

получаем

P (s, k) = B(s)s + k

A(s)s + k

A(s).

8.1 РЕГУЛЯТОРЫ НИЗКОГО ПОРЯДКА 205

Чтобы выявить более четко идею метода, рассмотрим простейший случай, когда

полиномы P

и P

фиксированы, а P

— интервальный полином. В приведенном вы-

ше примере ПИ-регулятора это соответствует случаю, когда числитель объекта A(s)

фиксирован, а знаменатель B(s) — интервальный полином. Тогда, как мы знаем (раз-

дел 7.1), P

(jω) изменяется в некотором прямоугольнике на комплексной плоскости (его

вершины определяются харитоновскими полиномами), поэтому при фиксированном ω

решения системы

(jω) + k

(jω) = −P

(jω)

относительно k

, k

изменяются в параллелограмме, вершины которого определяют-

ся решениями четырех харитоновских систем. Таким образом, каждая точка границы

D-разбиения размывается в параллелограмм. Точки внутри области устойчивости, не

накрываемые ни одним из этих параллелограммов, определяют значения k

, k

, гаран-

тирующие робастную стабилизацию.

Рассмотрим робастный вариант примера 4.2 из раздела 4.1. Для объекта с интер-

вальным знаменателем

G(s) =

s − 1

+ a

s + a

, 0, 8 ≤ a

≤ 1, 2; −0, 1 ≤ a

≤ 0, 1; 0, 8 ≤ a

≤ 1, 2,

мы ищем ПИ-регулятор

C(s) = k

+ k

/s,

гарантирующий робастную устойчивость. Характеристический полином замкнутой си-

стемы имеет вид

P (s, k) = a

s + a

+ a

+ k

s(s − 1) + k

(s − 1),

и уравнение границы D-разбиения P (jω) = 0 записывается следующим образом:

−k

− k

= a

−k

+ k

= −a

+ a

(8.1)

откуда

− (a

+ a

)ω

1 + ω

, k

(−a

− a

+ a

)

1 + ω

Задавая значения a = (a

), отвечающие четырем харитоновским полиномам:

= (0, 8 − 0, 1 1, 2), a

= (1, 2 − 0, 1 0, 8), a

= (1, 2 0, 1 0, 8), a

= (0, 8 0, 1 1, 2),

мы при фиксированном ω получим четыре точки k

, i = 1, . . . , 4, лежащие в вершинах

параллелограмма. При изменении ω эти параллелограммы зачертят полосу, в которую

размоется граница D-разбиения для невозмущенного объекта a

= (1 0 1) (на рис. 8.2

она показана жирной линией). Особая прямая k

= 0 не зависит от параметров a

остается одной прямой. Таким образом, область D

rob

робастной устойчивости на плос-

кости { k

, k

} приобретает вид, показанный на рис. 8.2. Разумеется, эта область меньше,

чем в случае невозмущенного объекта (ср. с рис. 4.4).

В данном случае (и в других аналогичных) можно было поступить и иначе, восполь-

зовавшись Теоремой 53 (регулятор первого порядка стабилизирует интервальный объ-

ект тогда и только тогда, когда он стабилизирует все харитоновские объекты). Иными

206 Глава 8. Робастная стабилизация и управление

ﬁgure=c:/sher/book/ﬁgs/8rdpart.eps,height=2.5in,width=3in

Рис. 8.2: Робастное D-разбиение. Область робастной устойчивости.

словами, можно построить D-разбиение по двум параметрам k

, k

для всех харитонов-

ских объектов; тогда пересечение всех областей устойчивости даст область робастной

устойчивости. Для данного примера D-разбиение дается гиперболами, получающимися

после исключения ω

из уравнений (8.1):

− a

)(k

+ a

)

+ a

+ k

и особой прямой k

= 0. Четыре области устойчивости (для четырех харитоновских

полиномов с коэффициентами

, i = 1, . . . , 4) показаны на рис. 8.3; их пересечение

определяет ту же область робастной устойчивости, что и на рис. 8.2. Идея робастного

ﬁgure=c:/sher/book/ﬁgs/8rdpart1.eps,height=2.5in,width=3in

Рис. 8.3: Робастное D-разбиение. Область робастной устойчивости как пересечение об-

ластей устойчивости четырех харитоновских объектов.

D-разбиения может быть применена и в более общем случае, когда полиномы A(s), B(s)

принадлежат семействам, отличным от интервальных, однако при этом техника по-

строения границы усложняется (граница порождается не параллелограммами, а более

сложными множествами).

Изложенные выше методы относились к стабилизации непрерывных систем. Их

можно отчасти перенести и на дискретный случай, но мы на этом не будем останавли-

ваться.

Возможны совсем другие подходы к синтезу робастных регуляторов низкого поряд-

ка, опирающиеся на численные методы. Пусть характеристический полином замкнутой

системы имеет вид

P (s, q, k), q ∈ Q.

Здесь, как и ранее, q — вектор неопределенных параметров, изменяющийся во мно-

жестве Q ⊂ R

, а k — коэффициенты регулятора. Будем считать, что k ∈ R

, т.е. мы

проектируем регулятор, зависящий от двух параметров. Тогда, для некоторого номи-

нального q

∈ Q можно с помощью D-разбиения найти область устойчивости в про-

странстве {k

, k

}, т.е. построить

= {k ∈ R

: P (s, q

, k) устойчив}.

Ясно, что множество всех робастно стабилизирующих регуляторов

rob

= {k ∈ R

: P (s, q, k) робастно устойчив для всех q ∈ Q}

является подмножеством D

: D

rob

⊂ D

. Генерируя точки k

∈ D

и пользуясь крите-

риями робастной устойчивости из раздела 7.1, можно проверять, будет ли k

∈ D

rob

Ясно, что можно организовать не только перебор точек из D

, но и построить более

эффективные методы поиска.

8.2. Робастная квадратичная стабилизация 207

8.2 Робастная квадратичная стабилизация

Рассмотрим ту же задачу, что и в разделе 4.4, но в робастном варианте. Для семей-

ства систем

˙x = A(q)x + Bu, q ∈ Q, (8.2)

мы пытаемся найти общий регулятор вида

u = Kx,

так, чтобы у замкнутых систем

˙x = A

(q)x, A

(q) = A(q) + BK, q ∈ Q,

была общая квадратичная функция Ляпунова

V (x) = x

P x, P > 0.

Зависимость матрицы A от параметров q может быть любой, например, это может быть

интервальное или аффинное семейство матриц (см. раздел 6.1). Как было показано в

Теореме 35, решение задачи для фиксированной A определяется решением одного ли-

нейного матричного неравенства. В случае неопределенной матрицы появляется набор

соответствующих неравенств, отвечающих всевозможным значениям параметра q.

Теорема 63 Если X — решение системы линейных матричных неравенств

(q) + A(q)X − 2BB

< 0, q ∈ Q, X > 0, (8.3)

то регулятор с матрицей

K = −B

−1

робастно стабилизирует систему (8.2), а квадратичная форма

V (x) = x

−1

является общей функцией Ляпунова для замкнутой системы при всех q ∈ Q.

Доказательство дословно повторяет доказательство Теоремы 35; заметим лишь, что

мы несколько изменили обозначения во избежание путаницы.

Таким образом, проблема сведена к решению линейных матричных неравенств. Их

может быть конечное число, если зависимость A(q) линейна, а Q — многогранник.

Действительно, если A(q), например, аффинное семейство

A(q) = A

i=1

, q ∈ Q

= {q ∈ R

: |q|

∞

≤ 1},

то неравенства (8.3) выполняются для всех q ∈ Q тогда и только тогда, когда они

выполняются для всех вершин q

∈ V

= {q ∈ Q : |q

| = 1, i = 1, . . . , `} куба Q. В

частности, если A(q) — интервальное семейство матриц, то достаточно решить систему

208 Глава 8. Робастная стабилизация и управление

линейных матричных неравенств, соответствующих вершинным матрицам, т.е. тем, у

которых все элементы принимают максимальные либо минимальные значения. Для

численного решения конечных систем линейных матричных неравенств существуют

мощные вычислительные методы; их можно найти, в частности, в пакете LMI Control

Toolbox системы Matlab. Тем не менее, число неравенств может быть слишком велико:

скажем, в случае интервальной матрицы n × n число неравенств равно 2

, и уже при

n = 5 применение таких методов наталкивается на трудности. В этих случаях могут

применяться более простые итеративные методы, которые на каждом шаге имеют дело

лишь с одним случайно генерируемым неравенством. При этом общее число неравенств

может быть бесконечным.

Мы рассмотрели лишь ситуацию, когда матрица A включает неопределенность, в то

время как матрица B известна точно. Более общий случай неопределенной матрицы B

также может быть сведен к линейным матричным неравенствам.

Сопутствующие функции Matlab:

quadstab (LMIC) — нахождение общей квадратичной функции Ляпунова и радиуса

квадратичной устойчивости для аффинного семейства на основе решения системы

линейных матричных неравенств.

8.3 Робастный линейно-квадратичный регулятор

Для той же модели неопределенности, что и в предыдущем разделе,

˙x = A(q)x + Bu, q ∈ Q, x(0) = x

рассмотрим задачу о линейно-квадратичном регуляторе. Мы хотим с помощью обрат-

ной связи

u = Kx

гарантировать некоторый уровень µ квадратичного критерия оптимальности

∞

(Rx, x) + (Su, u)

dt, J ≤ µ,

при всех значениях параметров q ∈ Q. Для простоты мы рассматриваем лишь случай,

когда матрицы B, R > 0, S > 0 известны точно, а неопределенность присутствует лишь

в матрице A. В разделе 5.1 были описаны различные способы решения задачи о линейно-

квадратичном регуляторе. Один из них (основанный на решении линейных матричных

неравенств (5.21)), допускает робастное обобщение.

Теорема 64 Пусть X(γ) — решение системы линейных матричных неравенств







A(q)X + XA

(q) + (γ − 2)BS

−1

1/2

X − I







≤ 0, X > 0, q ∈ Q. (8.4)

8.4 H

∞

-ОПТИМИЗАЦИЯ 209

Решим одномерную задачу минимизации

∗

= arg min

ϕ(γ), ϕ(γ) = γ

−1

X(γ)x

где минимизация ведется по всем γ > 0, для которых решение X(γ) существует.

Тогда для обратной связи

u = −S

−1

X(γ

∗

)

−1

гарантируется оценка критерия оптимальности

J ≤ ϕ(γ

∗

)

для всех значений параметра q ∈ Q.

Этот результат непосредственно следует из соответствующего результата при фик-

сированной матрице A из раздела 5.1. Таким образом, здесь необходимо решать (при

фиксированном γ) системы линейных матричных неравенств (8.4) при всех q ∈ Q. Как

уже отмечалось, если A(q) — аффинное семейство, а Q — многогранник, то достаточ-

но решить конечное число систем неравенств, отвечающих вершинам Q. Если таких

вершин слишком много, можно использовать специальные итеративные методы.

8.4 Робастная стабилизация с помощью H

∞

-оптимиза-

ции

В разделе 7.3 были приведены результаты, показывающие связь между робастной

устойчивостью замкнутой системы и условиями на ограниченность некоторых переда-

точных функций в H

∞

-норме. Например, из Теоремы 56 следует, что если передаточная

функция объекта имеет вид

G(s) = G

(s) + W

(s)∆(s)W

(s),

то робастная устойчивость при всех k∆(s)k

∞

≤ γ имеет место при условии

CSW

∞

где S = (I +G

−1

— чувствительность. Далее, пользуясь результатами об общем виде

стабилизирующих регуляторов (Теорема 29), мы заключаем, что

C = (X + V Q)(Y − UQ)

−1

S = (Y − UQ)(Y + UV

−1

X),

где Q — параметр Юлы (произвольная матричная функция из RH

∞

), а матрицы X, Y, U, V ∈

∞

определяются условиями

= UV

−1

, UX + V Y = I.

210 Глава 8. Робастная стабилизация и управление

Таким образом, условие робастной устойчивости записывается в терминах параметра

Юлы:

+ T

∞

= W

X(Y + UV

−1

X)W

, T

= W

V, T

= (Y + UV

−1

X)W

. (8.5)

В частности, задача о максимальной робастности (т.е. о нахождении максимального

уровня неопределенности γ, допускающего робастную стабилизацию), сводится к задаче

∞

-оптимизации

min

Q∈RH

∞

+ T

∞

, (8.6)

способы решения которой обсуждались в разделе 5.2. Таким образом, с принципиальной

точки зрения решение задачи о максимальной робастности выглядит так.

1. Для номинального объекта G

(s) находим его представление в виде G

= UV

−1

U, V ∈ RH

∞

; решаем уравнение UX + V Y = I и находим X, Y ; на их основе

вычисляем T

, T

по формулам (8.5).

2. Решаем задачу H

∞

-оптимизации (8.6), и пусть Q ∈ RH

∞

— ее решение, а kT

∞

= γ

∗

3. Строим регулятор

= (X + V Q)(Y − UQ)

−1

;

он является робастно стабилизирующим при всех 0 ≤ γ < γ

∗

Каждый из этапов может быть выполнен с помощью соответствующих процедур в

системе Мatlab.

Приведем еще несколько частных случаев, когда неопределенность задается не в

частотной, но в параметрической форме, однако возможно применение техники H

∞

оптимизации.

1. Комплексные параметры. Пусть передаточная функция одномерного объекта

имеет вид

G(s) =

(s) +

i=1

(s)

(s) +

i=1

(s)

, (8.7)

где A

, B

, i = 0, 1, . . . , `, — заданные полиномы, а q

, i = 1, . . . , `, — комплексные

параметры, изменяющиеся в шаре пространства C

i=1

≤ γ

, q

∈ C. (8.8)

Задача заключается в построении регулятора C(s) = N(s)/D(s), который робастно

стабилизирует объект (8.7)–(8.8). Отметим, что и в числителе, и в знаменателе стоят

одни и те же неопределенные параметры q

; это, однако, не является ограничением

(см. рассуждения в Главе 6). Необычно здесь то, что q

предполагаются комплексными;

впрочем, существуют задачи, в которых такая модель возникает естественным образом.