Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление

Подождите немного. Документ загружается.

7.4. µ-анализ 191

7.4 µ-анализ

Можно предложить единую схему, которая обобщает анализ робастной устойчивости

при разнообразных типах неопределенности, рассмотренных выше. Она называется µ-

анализом, поскольку в ее основу положено понятие так называемого структурного

сингулярного числа матрицы, обозначаемого µ.

Методология µ-анализа предполагает, что структура системы, содержащей объект,

регулятор, обратные связи, неопределенности, может быть преобразована к общему

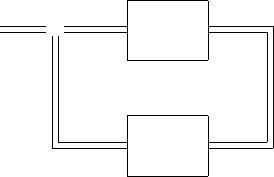
виду, называемому M–∆ конфигурацией, показанному на рис. 7.5; мы уже встречались

с частным случаем такой конфигурации в разделе 6.2 (см. рис. 6.1).

∆

Рис. 7.5: M–∆ конфигурация.

Здесь M — номинальная система (предполагающаяся устойчивой), а ∆ — все от-

носящееся к неопределенности. Заметим, что неопределенность здесь включена в цепь

обратной связи. Приведение системы, в которой первоначально структура совсем иная

(см., например, рис. 7.4 в центре и справа), к M–∆ конфигурации может быть вы-

полнено с помощью специальных приемов, хотя часто это отнюдь не простая задача.

При этом предполагается, что матрица ∆(s), задающая неопределенность, имеет специ-

альную структуру, которая будет описана позже. В качестве допустимых возмущений

рассматриваются устойчивые ∆(s), сохраняющие эту структуру и ограниченные в нор-

ме H

∞

k∆(s)k

∞

= sup

k∆(jω)k ≤ γ.

Нас интересует верхняя грань тех γ, при которых сохраняется робастная устойчивость

системы при описанных выше возмущениях. Поскольку система устойчива, если мат-

рица

I + M(s)∆(s)

−1

существует при Re s ≤ 0, то задача сводится к проверке условия

det

I + M(s)∆(s)

6= 0

при всех допустимых ∆(s) и всех s : Re s ≤ 0 (достаточно проверять лишь значения s,

лежащие на границе левой полуплоскости, т.е. s = jω). Условие

det

I + M(jω)∆(jω)

6= 0 ∀ ω

можно проверять “поточечно”, меняя ω. Поэтому возникает вопрос: как для постоянных

матриц M и ∆ проверить условие

det(I + M∆) 6= 0 ∀ ∆: k∆k ≤ 1,

192 Глава 7. Робастная устойчивость

причем имеются в виду ∆, обладающие специальной структурой. Все это мотивирует

введение следующих понятий.

Пусть M ∈ C

n×n

, т.е. M — постоянная квадратная матрица с комплексными эле-

ментами. Предположим, что все матрицы ∆ имеют следующую структуру:

∆ = diag

, . . . , r

, δ

m+1

, . . . , δ

m+s

, ∆

, . . . , ∆

, ∆

p+1

, . . . , ∆

p+f

где r

— вещественные числа, δ

— комплексные числа, ∆

, i = 1, . . . , p, — вещественные

квадратные матрицы, ∆

, i = p + 1, . . . , p + f, — комплексные квадратные матрицы,

а I

, . . . , I

m+s

— единичные матрицы некоторых фиксированных размерностей. Таким

образом, матрицы ∆ имеют блочно-диагональный вид: сначала идут блоки, пропор-

циональные единичным матрицам (они называются вещественными и комплексными

скалярными блоками), затем идут квадратные матрицы, у которых все элементы мо-

гут меняться (вещественные и комплексные полные блоки). Например, ∆ может иметь

следующую структуру:

∆ =













где r

, r

— вещественные числа, а δ

, δ

— комплексные. Размерность ∆ при этом равна

n × n (в данном примере n = 7). Число µ , соответствующее данной структуре матриц

(что будет обозначаться ∆ ∈ ∆) определяется так:

µ(M)

min

k∆k: ∆ ∈ ∆, det(I + M∆) = 0

−1

, (7.29)

причем если I + M∆ невырождена при всех ∆, то µ(M) = 0. Напомним, что k∆k здесь

обозначает спектральную норму, т.е. k∆k = σ

(∆) =

max

(∆

∗

∆)

1/2

, где σ

— наиболь-

шее сингулярное число, а λ

max

— наибольшее собственное значение эрмитовой матрицы.

Часто употребляют также обозначение µ

∆

(M), чтобы подчеркнуть зависимость от за-

данной структуры матриц ∆, но обычно из контекста ясно, о какой структуре идет

речь, и мы будем опускать индекс ∆. В простейших случаях µ(M) совпадает с извест-

ными из линейной алгебры величинами. Например, если есть лишь один скалярный

комплексный блок:

∆ = {δI, δ ∈ C},

то

∆

(M) = |λ

max

(M)| = ρ(M),

т.е. µ равно спектральному радиусу M. Действительно, det(I + M∆) = det(I + Mδ) = 0

только для δ = −1/λ

, где λ

— собственные значения M. Поэтому минимальное k∆k =

|δ|, при котором возможно такое равенство, равно 1/|λ

max

(M)|. Если же есть лишь один

полный комплексный блок, т.е.

∆ = {∆ ∈ C

n×n

7.4. µ-анализ 193

то µ

∆

(M) = σ

(M) = kMk. Это следует из Леммы 9: матрица I + M∆ невырождена,

если k∆k < 1/kMk, и она может потерять невырожденность при б´льших k∆k.

Интересно отметить, что µ(M) не меняется при некоторых преобразованиях подо-

бия. Именно, введем

D = diag {L

, . . . , L

, J

, . . . , J

, d

, . . . , d

p+f

}

где L

— вещественные матрицы (той же размерности, что и I

), L

= L

> 0; J

— ком-

плексные матрицы (той же размерности, что и I

m+i

), J

= J

∗

> 0; d

— положительные

вещественные числа.

Лемма 10 Для любого D ∈ D справедливо

µ(M) = µ(DMD

−1

Действительно, любые D ∈ D и ∆ ∈ ∆ коммутируют: D∆ = ∆D, поэтому

det(I + M∆) = det(I + MD

−1

D∆) = det(I + MD

−1

∆D) = det(I + DMD

−1

∆).

Последнее равенство использует тождество det(I +AD) = det( I +DA) (см. Приложение,

раздел 1).

Обозначим еще

= {U ∈ ∆: UU

∗

= I},

т.е. U — множество унитарных матриц той же структуры, что и ∆. Оказывается, для µ

можно получить верхние и нижние границы, используя линейные преобразования из U

и D.

Теорема 58 Справедлива оценка

sup

U∈U

ρ(UM) = µ(M) ≤ inf

D∈D

kDMD

−1

k (7.30)

Мы не будем доказывать эту теорему; она является основой для численного нахож-

дения µ(M). Минимизация по D в правой части (7.30) — сравнительно простая задача

(она может быть сведена к выпуклой оптимизации). В некоторых частных случаях (ко-

гда нет полных вещественных блоков и 2s + f ≤ 3, где s — число скалярных, а f —

полных комплексных блоков) в правой части (7.30) достигается равенство, т.е в этом

случае µ может быть вычислено эффективно. В общей ситуации верхняя и нижняя

границы для µ различаются. Особенно трудно вычисление µ для вещественных блоков,

которые соответствуют параметрическим неопределенностям. В системе Matlab суще-

ствует специальный пакет µ-Analysis and Synthesis Toolbox , где собраны эффективные

алгоритмы вычисления µ и его использования для анализа робастной устойчивости.

Подобное использование опирается на следующий результат.

Приведем замкнутую линейную систему, содержащую неопределенность, к M–∆

форме (рис. 7.5), где M(s) — передаточная функция номинальной системы (предпола-

гающаяся устойчивой, M(s) ∈ RH

∞

), а ∆( s) описывает все виды неопределенности в

194 Глава 7. Робастная устойчивость

системе, которые заданы блочно-диагональной структурой ∆. Это могут быть парамет-

рические неопределенности (им отвечают вещественные скалярные блоки), матричные

неопределенности (им отвечают вещественные полные блоки), частотные неопределен-

ности в H

∞

-норме (им отвечают комплексные полные блоки). При этом предполагается,

что ∆(s) ∈ RH

∞

и ∆ ∈ ∆ для всех s: Re s < 0.

Теорема 59 (критерий робастной устойчивости) Рассматриваемая система ус-

тойчива при всех допустимых ∆, k∆(s)k

∞

< γ, тогда и только тогда, когда

sup

M(jω)

≤

. (7.31)

Действительно, этот результат по-существу следует из теоремы о малом коэффици-

енте усиления и из определения µ; новым элементом является лишь структура неопре-

деленности (Теорема 56 относилась к одному полному комплексному блоку). Однако

схема доказательства остается во всех случаях прежней.

Итак, критерий робастной устойчивости, даваемый Теоремой 59, предполагает вы-

полнение следующих операций.

1. Система приводится к M–∆ конфигурации.

2. Для каждого ω вычисляется µ

M(jω)

3. Проверяется условие (7.31).

Здесь особенно трудоемким может оказаться второй этап; в случае вещественных неопре-

деленностей он особенно труден. Поэтому нельзя считать, что теорема является уни-

версальным способом проверки робастной устойчивости.

7.5 Вероятностный подход к робастной устойчивости

Как объяснено в разделе 6.4, возможен и часто целесообразен не минимаксный,

а вероятностный подход к робастности. Мы рассмотрим лишь задачи с параметриче-

ской неопределенностью (не вполне ясно, как ввести вероятностную меру в частотную

неопределенность). Итак, мы изучаем либо полиномы P(s, q), либо матрицы A(s, q),

зависящие от параметров q. По-прежнему будем предполагать, что параметры при-

надлежат множеству Q ⊂ R

, однако теперь на этом множестве задана вероятностная

мера. Для простоты будем считать, что задана плотность вероятности p(q), q ∈ Q. Если

эта плотность не задана по физическому смыслу задачи (см. замечания выше), то для

ограниченного множества Q естественно брать равномерную плотность на Q. Можно

показать, что такое распределение обладает рядом экстремальных свойств.

7.5.1 Метод Монте Карло

Простейший путь оценки вероятности устойчивости при заданной плотности p(q) за-

ключается в применении метода Монте-Карло. Именно, генерируется выборка q

, . . . , q

7.5. Вероятностный подход к робастной устойчивости 195

независимых случайных величин, имеющих плотность p(q). Для них вычисляются по-

линомы P (s, q

), . . . , P (s, q

) (или матрицы A(q

), . . . , A(q

)) и (с помощью критериев

устойчивости либо путем прямого вычисления корней или собственных значений) про-

веряется их устойчивость. Пусть число устойчивых полиномов (матриц) оказалось рав-

ным M ≤ N; если M близко к N, то можно надеяться, что вероятность устойчивости

высока. Чтобы формализовать такой подход, надо более строго уметь решать каждую

из задач — генерацию выборки q

, . . . , q

и оценки вероятности по частоте M/N. Оста-

новимся на этих вопросах подробнее.

а. Генерация равномерно распределенных векторов q ∈ Q. Если Q — куб

Q = {q ∈ R

: 0 ≤ q ≤ 1, i = 1, . . . , `},

то равномерное распределение генерируется чрезвычайно просто — достаточно неза-

висимо равномерно генерировать каждую компоненту q

вектора q. В Matlab’е такая

генерация вектора q производится одной командой q = rand(`, 1). Аналогично, гене-

рация равномерного распределения матриц в семействе интервальных матриц n × n,

0 ≤ a

≤ 1, производится командой rand(n). Разумеется, если Q — параллелепипед

{|q

− q

| ≤ r

, i = 1, . . . , `}, то нужно добавить к этому масштабирование и сдвиг

вектора q.

Если Q — шар

Q = {q ∈ R

: kqk

≤ 1},

то равномерно распределенные в Q случайные величины проще всего генерировать так:

q = ξ

1/`

kηk

где η ∈ R

— нормально распределенный вектор с нулевым средним и единичной ко-

вариационной матрицей, а ξ — равномерно распределенная на [0, 1] случайная вели-

чина, независимая от η. На языке Matlab’а это записывается так: η = randn(`, 1),

q = randˆ(1/`) ∗ η/norm(η). Таким же образом можно генерировать матрицы, ограни-

ченные по фробениусовой норме. Так, матричное семейство A = A

+ ∆, k∆k

≤ γ,

A ∈ R

n×n

, задается командами

η = randn(n), A = A0 + randˆ(1/nˆ2) ∗ γ ∗ η/norm(η,

fro

Существуют и способы генерации матриц, равномерно распределенных на шаре

k∆k ≤ γ, где k · k — спектральная норма.

б. Пусть задана последовательность бернуллиевских случайных величин ξ

, i = 1, . . . , N

(т.е. ξ

взаимно независимы, ξ

= 1 с вероятностью p, ξ

= 0 с вероятностью 1 − p) и

i=1

. Тогда удобная оценка p по частоте ˆp

= S

/N задается границами Чер-

нова

p ≥ ˆp

− ε

≥ 1 − e

−2ε

|p − ˆp

| ≥ ε

≤ 1 − 2e

−2ε

196 Глава 7. Робастная устойчивость

Применяя этот результат к проблеме робастной устойчивости, получаем следующий

способ оценки вероятности устойчивости. Пусть P (s, q) или A(q), q ∈ Q — полиноми-

альное или матричное семейство, зависящее от векторного параметра q ∈ Q ⊂ R

; q

i = 1, . . . , N, — равномерно распределенная на Q выборка, M — количество устойчи-

вых полиномов (матриц) из N выборочных, p — истинная вероятность устойчивости,

т.е. p = Vol(Q

)/Vol(Q), где Q

— область устойчивости, а Vol(·) означает объем мно-

жества. Тогда

p ≥

− ε

≥ 1 − e

−2ε

т.е. отношение M/N отклоняется от p больше, чем на ε с вероятностью, не превосхо-

дящей e

−2ε

. В частности, если M/N близко к единице, а N достаточно велико, то с

большой вероятностью можно заключить, что доля неустойчивых полиномов в Q мала.

Сопутствующие функции Matlab:

rand, randn — генерация равномерно распределенных и нормально распределенных

случайных чисел.

7.5.2 Вероятностные аппроксимации критериев робастной ус-

тойчивости

Для многих критериев робастной устойчивости, рассматривавшихся в разделах 7.1

и 7.2, можно построить их вероятностные аналоги. Продемонстрируем эти способы и

получающиеся при этом возможности на нескольких типах задач.

Для аффинного семейства полиномов

P (s, q) = P

(s) +

i=1

(s)

мы ранее предполагали, что параметры q

ограничены: q ∈ Q

= {q ∈ R

: |q

| ≤

γ, i = 1, . . . , `}, а критерий устойчивости для всех q ∈ Q заключался в том, что область

значений

S(ω) =

z ∈ C : z = P

(jω) +

i=1

(jω), q ∈ Q

не содержит нуля (в предположении, что P

(s) — устойчивый полином), см. Теорему 43.

Множество S(ω) — многоугольник, и возможно его точное описание (которое и приво-

дит к Теореме 46). Станем теперь на вероятностную точку зрения и будем считать q

независимыми равномерно распределенными на [−γ, γ] случайными величинами. Если

количество ` параметров достаточно велико, то сумма z = a

i=1

, a

= P

(jω), ве-

дет себя приблизительно как двумерная гауссовская случайная величина со средним a

и матрицей ковариаций W =

i=1

(здесь и далее комплексное число a

пони-

мается как двумерный вектор (Re a

, Im a

)

∈ R

). Поэтому S(ω) хорошо описывается

доверительным эллипсом

(ω)

z ∈ R

: (z − a

)

−1

(z −a

) ≤ τ

7.5. Вероятностный подход к робастной устойчивости 197

где τ задает доверительный уровень (ясно, что размер E

(ω) зависит также от разма-

ха γ неопределенности). Иными словами, если p

— соответствующая доверительная

вероятность, то

P (jω) ∈ E

(ω)

≈ p

для данного ω.

Важно отметить, что эллипс E

(ω) часто существенно меньше, чем вся область зна-

чений S(ω). Таким образом, если мы, опираясь на вероятностный аналог принципа ис-

ключения нуля (нуль не принадлежит E

(ω) для всех ω) оценим вероятностный радиус

устойчивости, т.е. максимально допустимое

= max

γ : 0 /∈ E

(ω) ∀ω

то окажется, что γ

> γ, где γ — “точный” (детерминированный) радиус устойчивости.

Иначе говоря, если пренебрегать событиями малой вероятности, то можно значитель-

но увеличить размах неопределенности параметров. Поскольку данный способ оцен-

ки радиуса устойчивости — приближенный, то окончательную проверку вероятности

устойчивости при выбранном γ можно провести с помощью метода Монте Карло.

Аналогичный способ можно применить в случае матричной неопределенности. Пусть

матрица A ∈ R

n×n

устойчива, а ее возмущения ∆ ∈ R

n×n

ограничены во фробениусовой

норме: k∆k

≤ γ. Для робастной устойчивости семейства A + ∆ требуется, чтобы

det(A − jωI + ∆) 6= 0 (7.32)

для всех ω ∈ R и k∆k

≤ γ. Поскольку

det(A − jωI + ∆) = det

A − jωI

´³

I + (A − jωI)

−1

∆

= det

A − jωI

det

I + (A − jωI)

−1

∆

то условие (7.32) эквивалентно условию

det

I + (A − jωI)

−1

∆

6= 0

для всех ω ∈ R и k∆k

≤ γ. Но для малых по фробениусовой норме матриц X имеем

det(I + X) ≈

i=1

(1 + x

) ≈ 1 + tr X,

поэтому

det

I + (A − jωI)

−1

∆

≈ 1 + tr

(A − jωI)

−1

∆

Иными словами, когда ∆ пробегает шар k∆k

≤ γ, точки z = 1 + tr

(A − jωI)

−1

∆

заполняют эллипс

(

z ∈ R

: (z −z

)

W (ω)(z − z

) ≤ 1

)

= (1, 0)

, W (ω) =

−1

∈ R

2×2

, B = B(ω) =

Re vec

(A − jωI)

−1

Im vec

(A − jωI)

−1

∈ R

2×n

198 Глава 7. Робастная устойчивость

(здесь vecM = (m

, . . . , m

)

— n

-мерный вектор, получающийся

вытягиванием в столбец n × n-матрицы M), который хорошо аппроксимирует область

S(ω)

z = det

I + (A − jωI)

−1

∆

, k∆k

≤ γ

Если теперь считать, что матрица ∆ равномерно распределена в шаре k∆k

≤ γ, то

можно показать, что при фиксированной комплексной матрице (A −jωI)

−1

двумерная

случайная величина ξ

= 1 + tr

(A − jωI)

−1

∆

имеет распределение с центром в z

(1, 0)

и линиями уровня которого являются эллипсы E

(ω):

(ω) =

(

z ∈ R

: (z −z

)

W (ω)(z − z

) ≤ τ

)

где τ задает доверительный уровень. Таким образом, приближенно можно считать, что

0 /∈ det(A − jωI + ∆) с вероятностью p = p

(соответствующей уровню τ), если

W (ω)z

> γ

= γ

(ω),

что дает максимальное значение γ

(ω) при данной частоте ω:

(ω) =

(ω)

1/2

Минимизируя по ω, мы получаем приближенное значение вероятностного радиуса устой-

чивости

= min

(ω).

Обычно γ

существенно больше, чем детерминированный радиус робастной устойчи-

вости. Вновь отметим, что заключительная оценка вероятности устойчивости при вы-

бранном γ может быть получена методом Монте Карло.

7.5.3 Свойства случайных матриц

Приведем еще один подход к робастной устойчивости матриц, основанный на неко-

торых теоремах о поведении случайных матриц.

Теорема 60 Пусть элементы ∆

матрицы ∆ размерности n ×n независимы и име-

ют равномерное распределение на [−γ, γ]. Тогда при n → ∞ спектральная норма мат-

рицы

√

∆ почти наверное стремится к 2, а ее собственные значения стремятся к

равномерному распределению на единичном круге.

Можно показать, что отсюда следует соотношение между вероятностным радиусом

устойчивости интервального семейства A + ∆ (∆

независимы и равномерно распре-

делены на [−γ, γ]) и вещественным радиусом устойчивости γ

max

(7.24) матрицы A:

случайное интервальное семейство робастно устойчиво с вероятностью 0, 99, если

γ ≤

0, 82

√

max

7.6. Выводы 199

Рассмотрим простейший пример, когда A = −I. Тогда интервальное семейство

−I + ∆ робастно устойчиво при γ < 1/n, а при γ ≥ 1/n устойчивость может потеряться

(дестабилизирующей является матрица с ∆

≡ 1/n). В то же время собственные зна-

чения матрицы −I + ∆ для случайного интервального семейства лежат приближенно

равномерно в круге с центром в −1 и радиуса γ

n/3, поэтому при γ <

3/n они будут

находиться в левой полуплоскости. Таким образом, соотношение размахов допустимых

возмущений для вероятностного и детерминированного подхода равно

√

3n.

7.6 Выводы

• Семейство полиномов

P(s, Q)

P (s, q) = a

(q) + a

(q)s + . . . + a

(q)s

, q ∈ Q ⊂ R

называется робастно устойчивым, если P (s, q) устойчивы при всех q ∈ Q.

Областью значений полиномиального семейства называется множество

S(ω)

P (jω, q): q ∈ Q

т.е. S(ω) — двумерный образ Q при отображении P (jω, ·). Многие критерии ро-

бастной устойчивости основаны на принципе исключения нуля: семейство робаст-

но устойчиво тогда и только тогда, когда Q связно, a

(q) 6= 0, в семействе су-

ществует устойчивый полином, и S(ω) не содержит нуля при всех значениях ω

(Теорема 43). Принцип справедлив и в дискретном случае, но здесь не требует-

ся, чтобы все полиномы P (z, q) имели одинаковую степень (отсутствует условие

(q) 6= 0). Доказательство основано на том, что при пересечении одним из кор-

ней границы устойчивости (мнимая ось либо единичная окружность) нарушается

условие 0 /∈ S(ω).

Для робастной устойчивости интервального семейства в непрерывном случае необ-

ходима и достаточна устойчивость четырех специальных вершинных полиномов

— харитоновских полиномов (Теорема 44 — теорема Харитонова). Область S(ω) в

этом случае — прямоугольник, вершины которого соответствуют харитоновским

полиномам, и доказательство основано на принципе исключения нуля и критерии

Михайлова. В дискретном случае аналогов Теоремы 44 нет.

Робастная устойчивость интервального полинома может быть установлена с по-

мощью графического критерия (Теорема 45). Здесь достаточно проверять поведе-

ние лишь одного годографа (годографа Цыпкина-Поляка); при этом определяется

максимальный размах γ

max

неопределенности, при котором сохраняется робаст-

ная устойчивость — радиус устойчивости. Аналогичный результат имеет место

для сферической неопределенности, в дискретном случае и др.

Критерий робастной устойчивости аффинного семейства полиномов

P(s, Q) = {P (s, q) = P

(s) + q

(s) + . . . + q

(s) : |q

| ≤ γ, i = 1, . . . , `},

200 Глава 7. Робастная устойчивость

дается реберной теоремой (Теорема 46): если полином P

(s) устойчив и deg P

≤

deg P

, i = 1, . . . , `, то (при некоторых дополнительных условиях регулярности)

для робастной устойчивости необходима и достаточна устойчивость всех реберных

полиномов, т.е. всех одномерных семейств вида

P (s, q): |q

| = γ, i 6= k, |q

| ≤ γ

Реберная теорема эффективно применима лишь если число ` неопределенных па-

раметров мало.

• Задача робастной устойчивости параметрических семейств матриц много слож-

нее задач для полиномов. Например, для интервального матричного семейства

отсутствуют аналоги теоремы Харитонова (устойчивость вершинных матриц не

гарантирует робастной устойчивости), для аффинного семейства неверна ребер-

ная теорема. Поэтому используют приближенные методы или формулируют до-

статочные условия робастности.

Один из приближенных методов использует идеи теории возмущений; он осно-

ван на Теореме 49, в которой оцениваются изменения собственных значений мат-

рицы A(q), зависящей дифференцируемым образом от вектора неопределенных

параметров q, вызванные малыми изменениями q. В ряде случаев (например, для

аффинного матричного семейства) это позволяет приближенно оценить величи-

ну минимального q, приводящего к потере устойчивости невозмущенной матрицы

A(0).

Среди достаточных условий робастной устойчивости матричных семейств при-

меняется подход, основанный на поиске общей квадратичной функции Ляпунова

для всего семейства A(q), q ∈ Q, т.е. на решении системы линейных матричных

неравенств

(q)P + P A(q) < 0, P > 0, q ∈ Q;

существование решения гарантирует робастную устойчивость A(q). В случае ин-

тервального или аффинного семейства такую систему неравенств достаточно ре-

шать лишь для вершин множества Q (для вершинных матриц семейства), т.е.

число неравенств конечно и равно 2

Другое достаточное условие заключается в использовании сверхустойчивости

вместо устойчивости. Например, если в интервальном семействе

A = ((a

)), a

= a

+ ∆

, |∆

| ≤ γ, i, j = 1 . . . , n,

номинальная матрица A

= ((a

)) сверхустойчива: σ(A

)

= min

−a

−

j6=i

0, то все семейство робастно сверхустойчиво, т.е.

−(a

+ ∆

) −

j6=i

+ ∆

| > 0, i = 1, . . . , n,

при всех |∆

| ≤ γ, тогда и только тогда, когда

γ < γ

∗

σ(A

)