Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление

Подождите немного. Документ загружается.

7.2. Робастная устойчивость матриц 181

Таким образом, мы в явном виде находим радиус сверхустойчивости интервального

семейства.

Аналогичные формулы справедливы и в дискретном случае: если kA

< 1, то

семейство матриц (7.22) остается сверхустойчивым при

γ < γ

∗

= min

1 −

а в случае m

≡ 1

∗

1 − kA

Известны и другие достаточные условия, дающие оценки снизу для радиуса устой-

чивости аффинного или интервального семейств матриц.

Перейдем теперь к другому типу матричных неопределенностей, задаваемых с по-

мощью матричных норм. Пусть

A = A

+ ∆, k∆k ≤ γ,

где матрица A

устойчива, и k·k означает спектральную норму. Нас интересует радиус

устойчивости такого семейства, т.е.

max

= sup{γ : A

+ ∆ устойчива при всех k∆k ≤ γ}.

Оказывается, такая задача очень трудна; ее решение было найдено лишь недавно, и мы

его приведем далее. В то же время, проблема существенно упрощается, если считать

возмущения ∆ комплексными. До сих пор мы рассматривали в основном матрицы с

вещественными элементами, поэтому упомянем о некоторых изменениях, возникающих

при переходе в комплексную область. Как и ранее, матрица A ∈ C

n×n

называется устой-

чивой, если все ее собственные значения λ

, i = 1, . . . , n, лежат в левой полуплоскости:

Re λ

< 0, i = 1, . . . , n. Характеристический полином P (s) = det(sI −A) такой матрицы

имеет, вообще говоря, комплексные коэффициенты. Спектральная норма матрицы A

равна

kAk = max

|x|

≤1

|Ax|

max

∗

1/2

а |x|

для комплексных векторов x вычисляется как |x|

= (x

∗

1/2

. Комплексным ра-

диусом устойчивости устойчивой матрицы A ∈ C

n×n

называется величина

max

= sup{γ : A + ∆ устойчива при всех ∆ ∈ C

n×n

, k∆k ≤ γ}.

Теорема 50 Комплексный радиус устойчивости определяется формулой

max

k(sI −A)

−1

∞

sup

k(jωI − A)

−1

182 Глава 7. Робастная устойчивость

Доказательство основывается на двух важных утверждениях, которые мы выделим

в виде лемм.

Лемма 8 Если A устойчива, а A + B неустойчива, то найдется такое 0 < λ ≤ 1,

что A + λB имеет чисто мнимое собственное значение, т.е.

det

jωI − (A + λB)

= 0

для некоторого ω ∈ R.

Доказательство. Действительно, полином P (s, λ)

= det

sI − (A + λB)

непрерывно

зависит от параметра λ, его степень всегда равна n, и мы можем воспользоваться теоре-

мой о непрерывной зависимости корней полинома от параметра. При переходе от всех

устойчивых корней (при λ = 0) к (по крайней мере одному) неустойчивому (при λ = 1)

траектория корня должна пересечь мнимую ось.

По-существу, мы уже пользовались этим рассуждением при доказательстве принци-

па исключения нуля для полиномов.

Лемма 9 Если матрица B ∈ C

n×n

невырождена, то при любом ∆ ∈ C

n×n

, k∆k <

1/kB

−1

k, матрица B + ∆ также будет невырожденной, а при γ ≥ 1/kB

−1

k найдется

такая ∆ ∈ C

n×n

, k∆k ≤ γ, что B + ∆ вырождена.

Доказательство. Если kDk ≤ q < 1, то (I + D)

−1

существует и k(I + D)

−1

k ≤ (1 −q)

−1

поскольку k(I + D)

−1

k = kI −D + D

−. . . k ≤ 1 + q + q

+ . . . = (1 − q)

−1

. Поэтому при

k∆k ≤ q/kB

−1

k, q < 1, имеем kB

−1

∆k ≤ q и

k(B + ∆)

−1

k = k(I + B

−1

∆)

−1

k ≤ kB

−1

kk(I + B

−1

∆)

−1

k ≤ kB

−1

1 − q

т.е. B + ∆ невырождена. Если же γ ≥ 1/kB

−1

k, то возьмем такое a, |a| = 1, что

−1

a| = kB

−1

k|a| (такое a существует по определению спектральной нормы матрицы),

и ∆ = −

a(B

−1

∗

−1

. Тогда k∆k = 1/kB

−1

k ≤ γ (так как для матрицы ранга один вида

∗

, x, y ∈ C

имеем kxy

∗

k = |x||y| ). С другой стороны, для b = B

−1

a 6= 0 будет

(B + ∆)b = a −

−1

∗

−1

a) = a − a = 0,

т.е. матрица B + ∆ — вырожденная.

Доказательство Теоремы 50. Предположим, что k∆k < γ

max

, но A + ∆ неустойчива.

Тогда по Лемме 8 найдется ∆

= λ∆, k∆

k < γ

max

, и ω ∈ R такие, что матрица B + ∆

= −A + jωI, вырождена. Однако это противоречит первому утверждению Леммы 9

(так как k∆

k < γ

max

≤ 1/kB

−1

k при любом ω). Обратно, если γ ≥ γ

max

, то найдется

такое ω, что для B = −A + jωI будет γ ≥ kB

−1

k. Применяя вторую часть Леммы 9,

найдем такое допустимое ∆, что det(−A + jωI + ∆) = 0; это означает, что матрица

A + ∆ имеет чисто мнимое собственное значение jω и потому неустойчива.

7.2. Робастная устойчивость матриц 183

Заметим, что в ходе доказательства мы обнаружили, что дестабилизирующее воз-

мущение ∆ при γ ≥ γ

max

может быть взято в виде матрицы ранга один.

Приведем без доказательства (оно подобно вышеприведенному) аналогичную фор-

мулу для радиуса комплексной устойчивости для более общей схемы неопределенности,

так называемой структурированной неопределенности (см. раздел 6.1). Пусть матри-

ца A ∈ C

n×n

устойчива; нас интересует наибольшее число γ

max

такое, что все матрицы

вида

A + B∆C, ∆ ∈ C

m×l

, k∆k ≤ γ, (7.23)

являются устойчивыми. Здесь B ∈ C

n×m

, C ∈ C

l×n

— заданные матрицы. Такие задачи

естественно возникают, когда есть неопределенность в цепи обратной связи. Ясно, что

при B = C = I мы имеем предыдущую задачу.

Теорема 51 Комплексный радиус устойчивости семейства (7.23) равен

max

kG(s)k

∞

sup

kG(jω)k

, G(s)

= C(sI − A)

−1

Вспоминая связь между H

∞

-нормой и решением соответствующего уравнения Рик-

кати (см. Лемму П.22 из Приложения), мы заключаем, что уравнение Риккати

P A + A

∗

P − γC

∗

C − P BB

∗

P = 0

имеет эрмитово решение P = P

∗

> 0 тогда и только тогда, когда γ < γ

max

. Более того,

решение P этого уравнения позволяет построить общую функцию Ляпунова V (x) =

∗

P x для всех систем ˙x = (A + B∆C)x, k∆k ≤ γ < γ

max

Ситуация с вещественным радиусом устойчивости

max

= sup{γ : A + B∆C устойчива при всех ∆ ∈ R

m×l

, k∆k ≤ γ}, (7.24)

где

A, B, C

— вещественные матрицы и

устойчива, гораздо более сложна. Конечно,

мы имеем оценку

max

≥ γ

max

(поскольку комплексные возмущения включают в себя вещественные). Однако уже про-

стые примеры (с n = 2, B = C = I) показывают, что отношение γ

max

/γ

max

может быть

сколь угодно велико, т.е. вышеприведенная оценка может быть плохой.

Известны и другие достаточные условия робастной устойчивости вещественного се-

мейства A + B∆C, однако и они обладают тем же недостатком. Выражение для γ

max

было получено лишь недавно; для его формулировки напомним определение сингу-

лярных чисел матрицы (см. также Приложение, раздел 6.5). Для n × n матрицы A

упорядоченные собственные числа 0 ≤ λ

≤ . . . ≤ λ

симметричной матрицы A

(эти собственные числа вещественны и неотрицательны, так как A

A ≥ 0) определяют

сингулярные числа A:

(A) = λ

1/2

, i = 1, . . . , n.

184 Глава 7. Робастная устойчивость

Нетрудно видеть, что kAk = σ

(A) и 1/kA

−1

k = σ

(A), так что результат Теоремы 50

может быть записан следующим образом:

max

sup

(jωI − A)

−1

= inf

(jωI − A). (7.25)

В терминах сингулярных чисел записывается и выражение для вещественного радиуса

устойчивости.

Теорема 52 Обозначим U(ω)

= Re (jωI − A)

−1

, V (ω)

= Im (jωI − A)

−1

и составим

блочную матрицу

H(ω, α)







U(ω) − αV (ω)

−1

V (ω) U(ω)







зависящую от двух вещественные параметров ω, α. Тогда

max

= inf

inf

α∈(0,1]

n−1

H(ω, α)

В отличие от Теоремы 50 (в форме (7.25)) здесь фигурируют два скалярных па-

раметра (а не один), по которым нужно проводить оптимизацию; кроме того, нужно

вычислять не крайнее, а второе по порядку сингулярное значение матрицы. Ясно, что

в вычислительном смысле нахождение вещественного радиуса устойчивости — более

трудная задача, чем комплексного. Отметим также, что дестабилизирующими возму-

щениями являются матрицы второго ранга, а не первого.

В заключение заметим, что все результаты данного раздела естественно обобщаются

на случай дискретных систем. Например, если матрица A дискретно устойчива, то

комплексный радиус устойчивости семейства

A + ∆, k∆k ≤ γ,

равен

max

k(sI −A)

−1

∞

max

0≤ω<2π

k(e

jω

I −A)

−1

= min

0≤ω<2π

jω

I −A

что является дискретным аналогом Теоремы 50.

Сопутствующие функции Matlab:

svd — сингулярное разложение матрицы и вычисление сингулярных значений

7.3 НЕОПРЕДЕЛЕННОСТЬ В ПЕРЕДАТОЧНОЙ ФУНКЦИИ 185

7.3 Робастная устойчивость при неопределенных пе-

редаточных функциях

В разделах 6.1 и 6.2 обсуждались возможные виды неопределенности при описании

объектов с помощью передаточных функций; приведем критерии робастной устойчи-

вости соответствующих семейств замкнутых систем.

Начнем с простейшей задачи об устойчивости одномерных систем, заданных пе-

редаточной функцией, зависящей от параметров. Объект описывается передаточной

функцией

G(s, q) =

a(s, q)

b(s, q)

q ∈ Q,

где a(s, q), b(s, q) — полиномы, зависящие от параметров q ∈ Q, а регулятор в цепи

обратной связи имеет передаточную функцию

C(s) =

f(s)

g(s)

где f(s), g(s) — заданные полиномы (в этом разделе полиномы обозначаются строчными

буквами). Нас интересует робастная устойчивость (т.е. устойчивость при всех q ∈ Q)

замкнутой системы. Характеристический полином в данном случае равен

p(s, q) = a(s, q)f(s) + b(s, q)g(s),

и задача сводится к проблеме устойчивости параметрического семейства полиномов,

изученной в разделе 7.1. Мы отметим лишь некоторые особенности возникающих задач.

Во-первых, если a(s, q), b(s, q) — интервальные полиномы, то p(s, q) таковым не яв-

ляется, и никакого аналога теоремы Харитонова в общей ситуации нет. Однако в неко-

торых специальных случаях “вершинные” теоремы все же имеют место. Назовем хари-

тоновскими 16 передаточных функций G

(s), i = 1, . . . , 16, (соответствующих харито-

новским объектам), которые получаются из G(s, q), когда в числителе и знаменателе

берутся харитоновские полиномы.

Теорема 53 Если a(s, q), b(s, q) — интервальные полиномы, а регулятор C(s) — пер-

вого порядка

C(s) =

+ f

+ g

и он стабилизирует 16 харитоновских объектов, то он стабилизирует все интер-

вальное семейство.

Доказательство достаточно сложно, и мы его не приводим.

В более общем случае, для регулятора произвольного порядка, можно воспользо-

ваться тем фактом, что область значений полинома p(s, q) (т.е. S(ω)

= {p(jω, q), q ∈ Q},

см. раздел 7.1) является восьмиугольником. Действительно, области значений интер-

вальных полиномов a(s, q), b(s, q) являются прямоугольниками, потому сумма f(jω)a(jω, q)+

g(jω)b(jω, q) является восьмиугольником. На этой основе нетрудно выписать эффектив-

ный критерий робастной устойчивости.

186 Глава 7. Робастная устойчивость

Во-вторых, если a(s, q), b(s, q) — аффинные семейства, то и p(s, q) будет аффинным

семейством полиномов, и мы можем применить результаты раздела 7.1 для установ-

ления его робастной устойчивости. В частности, справедлива реберная теорема, и мы

получаем следующий результат.

Теорема 54 Если a(s, q), b(s, q) — аффинные семейства, и все реберные объекты (по-

лучающиеся, когда q пробегает ребро параллелепипеда Q) устойчивы, то имеет место

робастная устойчивость.

Есть и несколько других частных случаев, когда, используя конкретный вид p(s, q),

можно получить специальные критерии робастной устойчивости. Не будем на этом оста-

навливаться, а перейдем к непараметрической неопределенности одномерных переда-

точных функций.

Пусть открытая система описывается семейством скалярных передаточных функций

H(s) = H

(s) + ∆(s),

где частотная неопределенность ∆(s) удовлетворяет условию

|∆(jω)| ≤ ν|W (jω)| (7.26)

при всех ω для некоторой функции W (s), W

−1

(s) ∈ RH

∞

, что эквивалентно условию

−1

(s)∆(s)k

∞

≤ ν.

Нас интересует, будет ли робастно устойчива такая система, замкнутая единичной об-

ратной связью. Как известно (см. раздел 3.4), при отсутствии неопределенности вопрос

решается с помощью годографа Найквиста. Приведем его робастную модификацию.

Теорема 55 Пусть неопределенности ∆(s) удовлетворяют (7.26), и все H(s) = H

(s)+

∆(s) имеют одинаковое число N неустойчивых полюсов при всех допустимых ∆(s).

Построим годограф

H(jω) =

(jω) + 1

|W (jω)|

− 1, 0 ≤ ω < ∞.

Замкнутая система робастно устойчива тогда и только тогда, когда годограф

H(jω)

охватывает круг C

с центром в точке −1 и радиуса ν N/2 раз против часовой стрел-

ки, не пересекая его (рис. 7.3).

Доказательство. Покажем, что при сделанных предположениях для каждой допу-

стимой функции H( s) выполняется критерий Найквиста. Действительно, условие, что

H(jω) не пересекает C

, означает |

H(jω) + 1| > ν, т.е. |H

(jω) + 1| > ν|W (jω)| для

всех ω. Поэтому для любого допустимого H(s) имеем

|H(jω) + 1 | = |H

(jω) + 1 + ∆(jω)| ≥ | H

(jω) + 1|−|∆(jω)| > ν|W (jω)|−ν|W (jω)| = 0,

7.3 НЕОПРЕДЕЛЕННОСТЬ В ПЕРЕДАТОЧНОЙ ФУНКЦИИ 187

т.е. H(jω) не проходит через точку −1. Далее, годографы H

(jω) и

H(jω) пересека-

ют луч (−1, −∞) одинаковое число раз и в одинаковых направлениях (сверху вниз

или снизу вверх). Действительно, если H

(jω) вещественно и H

(jω) < −1, то

H(jω) =

(jω) + 1

|W (jω)|

− 1 < −1; при этом, если H

(jω)

= U

+jV

H(jω)

= U +jV то V =

|W (jω)|

т.е. знаки мнимых частей

H(jω) и H

(jω) совпадают. Поэтому число оборотов вокруг

точки −1 для

H(jω) и H

(jω) одинаково. Но все годографы H(jω) делают одинако-

вое число оборотов вокруг точки −1 (число оборотов может измениться только при

прохождении одного из годографов семейства H(jω) через точку −1, однако как было

доказано, H(jω) не проходит через −1 для всех допустимых H(s)). Итак, все годографы

(jω),

H(jω), H(jω) делают N/2 оборотов вокруг точки −1 против часовой стрелки.

По критерию Найквиста отсюда следует устойчивость замкнутой системы с передаточ-

ной функцией H(s), т.е. робастная устойчивость рассматриваемого семейства.

ﬁgure=c:/sher/book/ﬁgs/7robnyq1.eps,height=2.5in,width=3in

Рис. 7.3: Робастный критерий Найквиста. Поведение годографа

H(jω)

Теперь докажем обратное утверждение: если годограф

H(jω) пересекает круг C

или делает вокруг него число оборотов, отличное от N/2, то устойчивость нарушается.

Действительно, вторая возможность исключается, так как мы доказали выше, что ес-

ли

H(jω) не пересекает C

, то число оборотов

H(jω) и H

(jω) одинаково, а последнее

равно N/2. Если же

H(jω) пересекает C

, то при некотором ω будет |

H(jω) + 1| = ν,

т.е. |H

(jω) + 1| = ν|W (jω)|. Тогда, взяв

∆(s) = νW (s)e

jθ

, θ = −π + arg W

−1

(jω)(H

(jω) + 1),

получим kW

−1

∆k

∞

= ν, ∆ ∈ RH

∞

(так как W ∈ RH

∞

), и все H( s) = H

(s) + ∆ имеют

то же число неустойчивых полюсов, что и H

(s). Поэтому ∆ — допустимое возмущение.

Однако

|H(jω) + 1| = |H

(jω) + νW (jω)e

jθ

+ 1| = 0

(так как |H

(jω) + 1| = ν|W (jω)e

jθ

|, arg(H

(jω) + 1) = −arg(νW (jω)e

jθ

)), т.е. H(jω)

проходит через точку −1 и тем самым (по обычному критерию Найквиста) соответ-

ствующая замкнутая система является неустойчивой.

Отметим, что полученной теореме можно придать и аналитическую форму: если

номинальная система (с передаточной функцией H

(s) разомкнутой части) устойчива,

то робастная устойчивость рассматриваемого семейства эквивалентна условию

(jω) + 1| > ν|W (jω)|

для всех ω или

−1

(s)(H

(s) + 1)k

∞

> ν. (7.27)

Действительно, условие непересечения

H(jω) с кругом C

означает, что |

H(jω)+1| > ν,

что в свою очередь эквивалентно (7.27).

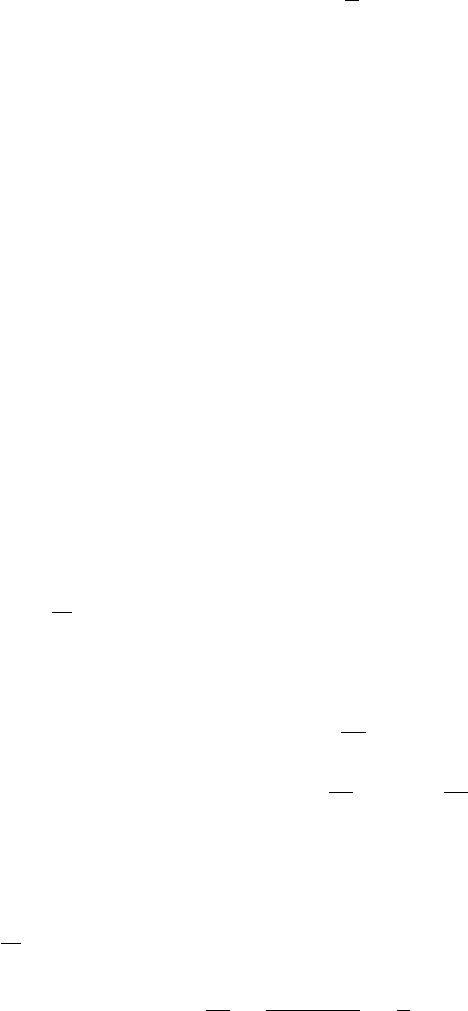
188 Глава 7. Робастная устойчивость

Перейдем теперь к анализу робастной устойчивости многомерных систем при ча-

стотной неопределенности. Мы начнем с важного вспомогательного результата, играю-

щего роль Теоремы 55 для матричных передаточных функций.

Теорема 56 (о малом коэффициенте усиления) Пусть M(s) ∈ RH

∞

. Матрица

I + M(s)∆(s)

−1

определена и принадлежит RH

∞

при всех

∆ ∈ RH

∞

, k∆(s)k

∞

≤

тогда и только тогда, когда kM(s)k

∞

< γ.

Доказательство. Необходимость. Поскольку ∆ ∈ RH

∞

и M ∈ RH

∞

, то и M∆ ∈ RH

∞

Поэтому по Теореме 12 (I + M∆)

−1

∈ RH

∞

тогда и только тогда, когда det(I + M∆)

не имеет корней в правой полуплоскости. Но при kMk

∞

< γ имеем (обозначая σ

и σ

наименьшие и наибольшие сингулярные числа соответствующих матриц):

inf

Re s≥0

I + M(s)∆(s)

≥ 1 − sup

Re s≥0

M(s)∆(s)

= 1 − kM∆k

∞

≥ 1 − kMk

∞

k∆k

∞

> 1 − γ · (1/γ) = 0,

т.е. действительно матрица I + M(s)∆(s) невырождена при Re s ≥ 0.

Достаточность. Пусть kMk

∞

≥ γ, тогда найдется такое ω, что kM(jω)k ≥ γ. Пусть

сингулярное разложение матрицы M(jω) (см. раздел 6.5 Приложения) имеет вид

M(jω) = USV

∗

где U, V — унитарные комплексные матрицы, а S = diag (σ

, . . . , σ

); здесь 0 ≤ σ

≤

≤ . . . ≤ σ

= kM(jω)k — сингулярные числа M(jω). Обозначим через u и v послед-

ние столбцы матриц U и V ; тогда если нам удастся построить ∆(s) ∈ RH

∞

такое, что

k∆(s)k

∞

≤ 1/γ, ∆(jω) = −

∗

, то матрица I + M∆ будет вырожденной. Действи-

тельно, используя равенство det(I + xy

∗

) = 1 + y

∗

x для x, y ∈ C

(см. Приложение,

раздел 1), получаем

det

I + M(jω)∆(jω)

= det

I −UCV

∗

= 1 − u

∗

USV

∗

= 1 −

= 0

(в последнем равенстве использовалось u

∗

U = V

∗

v = e

= (0, . . . , 0, 1)

). Требуемое

∆(s) построим следующим образом:

а). Если ω = 0 или ω = ∞, то M(jω) вещественно, потому и U, V вещественны и

можно взять ∆(s) ≡ −

, т.е. ∆(s) в этом случае не зависит от s. Очевидно, что

тогда

k∆(s)k

∞

= k∆k =

kM(jω)k

≤

и ∆ ∈ RH

∞

7.3 НЕОПРЕДЕЛЕННОСТЬ В ПЕРЕДАТОЧНОЙ ФУНКЦИИ 189

б). Если 0 < ω < ∞, то найдем α

≥ 0, β

≥ 0 из условий

arg

− jω

+ jω

= arg u

, arg

− jω

+ jω

= arg v

где u

, v

— компоненты векторов u, v, а аргумент в данном случае понимается как угол

от −π до 0. Теперь возьмем

∆(s)

= −

a(s)b

∗

(s), a(s) = [a

(s), . . . , a

(s)]

, b(s) = [b

(s), . . . , b

(s)]

;

(s) = v

− s

+ s

, b

(s) = u

− s

+ s

Тогда такое ∆(s) — желаемое, так как

α − s

α + s

∞

= max

α − jω

α + jω

¯= 1,

α − s

α + s

∈ RH

∞

при

α > 0, поэтому ∆(s) ∈ RH

∞

, k∆k

∞

≤

, а равенство ∆(jω) = −

∗

прове-

ряется прямой подстановкой (в силу определений a(s), b(s)). Итак, теорема доказана

полностью.

Отметим некоторые частные случаи теоремы о малом коэффициенте усиления и ее

связь с предыдущими результатами.

Прежде всего, Теорема 55 (в форме неравенства (7.27), а не в графической интерпре-

тации) является одномерным вариантом этого утверждения. Действительно, устойчи-

вость замкнутой системы, рассматриваемой в Теореме 55, определяется устойчивостью

ее передаточной функции S(s)

1+H(s)

−1

. Обозначая

1+H

(s)

−1

= M(s) ∈ RH

∞

получаем S(s) = M(s)

1+M(s)∆(s)

−1

, т.е. условие S(s) ∈ RH

∞

эквивалентно условию

1 +M(s)∆(s)

−1

∈ RH

∞

; именно это условие и рассматривается (в матричном вариан-

те) в теореме о малом коэффициенте усиления. Для W (s) ≡ 1 требование kM(s)k

∞

≤ γ

в последней в точности эквивалентно (7.27), а ограничения на ∆ в обеих теоремах сов-

падают при ν = 1/γ. В то же время в скалярном случае было доказано несколько более

общее утверждение — там не предполагалось, что ∆ ∈ RH

∞

, а требовалось лишь, что-

бы H

(s) + ∆(s) и H

(s) имели одинаковое число неустойчивых полюсов. Иначе говоря,

класс возмущений в Теореме 55 — несколько более общий, чем в многомерном случае.

Попробуем теперь сравнить результат, даваемый теоремой о малом коэффициенте

усиления, с формулой для комплексного радиуса устойчивости. Поскольку матрица

устойчива тогда и только тогда, когда обратная существует и устойчива, а

(A + ∆)

−1

= A

−1

(I + A

−1

∆) = A

−1

(I + M∆), M

= A

−1

то устойчивость A + ∆ эквивалентна устойчивости I + M∆. Поэтому на первый взгляд

кажется, что из теоремы о малом коэффициенте усиления следует, что радиус устойчи-

вости равен 1/kMk = 1/kA

−1

k, тогда как в действительности он равен k(sI −A)

−1

∞

≥

1/kA

−1

k. Дело в том, что в двух теоремах рассматривались разные классы возмуще-

ний: в теореме о радиусе устойчивости возмущения ∆ были постоянными матрицами,

тогда как в теореме о малом коэффициенте усиления рассматривались динамические

190 Глава 7. Робастная устойчивость

возмущения ∆(s). Этот класс более широк, поэтому радиус устойчивости получается

меньшим.

Из теоремы о малом коэффициенте усиления можно получить много следствий для

различных типов неопределенности и различных структур объектов. Мы приведем их

без доказательств, которые сводятся к преобразованию в форму, описываемую Теоре-

мой 56 и проверке ее условий. Всюду далее G(s) — матричная передаточная функция

объекта; G

(s) — ее номинальное значение; C(s) — матричная передаточная функция

регулятора; ∆(s) — матричная неопределенность, причем предполагается, что

∆(s) ∈ RH

∞

, k∆k

∞

≤ 1; (7.28)

, W

— заданные матричные весовые функции;

= (I + G

−1

, T

= I −S = G

C(I + G

−1

— чувствительность и дополнительная чувствительность номинальной системы, пока-

занной на рис. 7.4 слева (она предполагается устойчивой).

+ W

∆W

Рис. 7.4: Различные типы неопределенности и структур объектов.

Теорема 57

а). Если неопределенность входит аддитивно

G = G

+ W

∆W

(см. рис. 7.4 в центре), то условие робастной устойчивости имеет вид

CSW

∞

< 1.

б). Если неопределенность входит мультипликативно

G = (I + W

∆W

(см. рис. 7.4 справа), то условие робастной устойчивости записывается так:

T W

∞

< 1.

В простейшей ситуации при W

= W

≡ I условия робастной устойчивости при всех

возмущениях, удовлетворяющих (7.28), принимают вид

kCSk

∞

< 1

в аддитивном случае и

kT k

∞

< 1

в мультипликативном случае. Аналогичные результаты можно получить и для других

моделей неопределенности.

Сопутствующие функции Matlab:

svd — сингулярное разложение матрицы и вычисление сингулярных значений