Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление

Подождите немного. Документ загружается.

8.4 H

∞

-ОПТИМИЗАЦИЯ 211

Пусть передаточная функция номинального объекта G

(s) = A

(s)/B

(s) реализуе-

мая (т.е. deg A

≤ deg B

), полиномы A

, B

взаимно просты, deg A

< deg A

, deg B

deg B

, i = 1, . . . , `. Составим матрицу W (s) размерности ` × 2

W (s) =







(s)







первый столбец которой обозначим W

(s), а второй W

(s). Обозначим еще, как обычно,

через S(s) и T (s) чувствительность и дополнительную чувствительность номинального

объекта:

S(s) =

1 + G

(s)C(s)

, T (s) =

(s)C(s)

1 + G

(s)C(s)

Пусть γ

∗

— решение задачи

∗

= min

S + W

T k

∞

. (8.9)

Эта задача эквивалентна задаче H

∞

-оптимизации стандартного вида (см. (6.15))

min

(P, C)k

∞

для условного объекта

P (s) =







(s) G

(s)

(s) − W

(s)

1 −G

(s)







и ее решение может быть найдено описанными в разделе 5.2 средствами.

Теорема 65 Пусть γ

∗

, C — решение задачи (8.9). Тогда при γ < γ

∗

регулятор C ро-

бастно стабилизирует объект (8.7)–(8.8).

Мы не будем приводить всех технических деталей доказательства; подчеркнем лишь

основную идею. Характеристический полином замкнутой системы имеет вид

Ψ(s, q) =

(s) +

i=1

(s)

N(s) +

(s) +

i=1

(s)

D(s)

= Ψ

(s) +

i=1

(s)N(s) + B

(s)D(s)

и если регулятор стабилизирует номинальный объект, то Ψ

(s) гурвицев, и в соответ-

ствии с принципом исключения нуля (раздел 7.1) робастная устойчивость имеет место

при

1 +

i=1

(jω)N(jω) + B

(jω)D(jω)

(jω)

6= 0

212 Глава 8. Робастная стабилизация и управление

для всех ω ≥ 0 и всех q

, удовлетворяющих (8.7). Заметим, что для любых фиксирован-

ных c

∈ C, i = 1, . . . , `, множество

S =

z =

i=1

≤ γ

, q

∈ C

является кругом с центром в нуле и радиусом γ

i=1

1/2

на комплексной плоскости.

Итак, робастная устойчивость имеет место тогда и только тогда, когда

sup

ω≥0

i=1

(jω)N(jω) + B

(jω)D(jω)

(jω)N(jω) + B

(jω)D(jω)

С помощью несложных преобразований последнее условие может быть записано в стан-

дартной H

∞

форме, что и сделано в теореме.

2. Дискретные системы с l

-неопределенностью. Пусть передаточная функция дис-

кретного объекта имеет вид

G(z) =

A(z) + ∆A(z)

B(z) + ∆B(z)

, (8.10)

где неопределенности — полиномы ∆A(z), ∆B(z) — ограничены в l

-норме, но их сте-

пени не ограничены:

k∆Ak

+ k∆Bk

≤ γ

. (8.11)

Такие неопределенности уже рассматривались в разделе 7.1, см. (7.16). Мы упоминали

там, что области значений таких полиномов — круги на комплексной плоскости. Ис-

пользуя этот факт и рассуждая примерно так же, как при доказательстве Теоремы 65,

приходим к следующему результату.

Составим

S(z)

1 + G

(z)C(z)

, T (z)

(z)C(z)

1 + G

(z)C(z)

где C(z) — искомая передаточная функция регулятора, G

(z) = A(z)/B(z) — переда-

точная функция номинального объекта и положим

(z)

B(z)

, W

(z)

A(z)

Робастная устойчивость имеет место тогда и только тогда, когда

∞

Таким образом, если мы решим задачу H

∞

-оптимизации

∗

= min

∞

и обозначим полученный оптимальный регулятор через C, то при γ < γ

∗

этот регулятор

робастно стабилизирует объект (8.10)–(8.11).

8.4 H

∞

-ОПТИМИЗАЦИЯ 213

3. Вещественная неопределенность. Мы вновь возвращаемся к непрерывным систе-

мам и рассматриваем ту же модель объекта, что и (8.7), но с вещественными парамет-

рами:

G(s) =

(s) +

i=1

(s)

(s) +

i=1

(s)

i=1

≤ γ

, q

∈ R. (8.12)

Такую задачу не удается свести к стандартной H

∞

-задаче, но тем не менее, ее уда-

ется записать в виде некоторой выпуклой задачи родственного типа. Именно, составим

(s) =

A(s)

P (s)

, H

(s) =

B(s)

P (s)

где P (s) — устойчивый полином, такой что

P (−s)P (s) = A(−s)A(s) + B(−s)B(s),

найдем X, Y как решение уравнения

X + H

Y = 1,

и составим матрицу

(s) W

(s)

P (s)







(s) B

(s)

(s) B

(s)







Теорема 66 (Ранцер-Мегрецкий) Если найдутся Q

, Q

∈ RH

∞

, удовлетворяю-

щие неравенству

(

(jω) W

(jω)

Y (jω) − H

(jω)

−X(jω) H

(jω)

!Ã

(jω)

< Re Q

(jω) (8.13)

для всех ω ≥ 0, то регулятор

C =

Y Q

− H

робастно стабилизирует систему (8.12).

Мы не приводим доказательство этого результата, так как оно достаточно сложно.

Неравенство (8.13) выпукло относительно переменных Q

, Q

∈ RH

∞

, играющих ту же

роль, что и параметр Юлы. Не совсем ясно, как решать выпуклую систему неравенств

такого типа — ведь переменными являются не конечномерные векторы, а устойчивые

передаточные функции. Один из возможных путей заключается в конечномерной ап-

проксимации таких функций.

214 Глава 8. Робастная стабилизация и управление

8.5 µ-синтез

В разделе 7.4 мы видели, что устойчивость системы при фиксированном регуля-

торе и различных видах неопределенности можно исследовать с помощью µ-анализа.

Именно, Теорема 59 дает необходимое и достаточное условие робастной устойчивости

системы, имеющей M–∆ конфигурацию (рис. 7.5), в терминах структурного сингуляр-

ного числа µ(M): при всех возмущениях k∆(s)k

∞

< γ заданной структуры робастная

устойчивость имеет место тогда и только тогда, когда

sup

ω≥0

M(jω)

≤

. (8.14)

В этом разделе мы будем решать задачу выбора регулятора C, который обеспечивает

выполнение условия (8.14). Вспомним, что M(s) соответствует передаточной функции

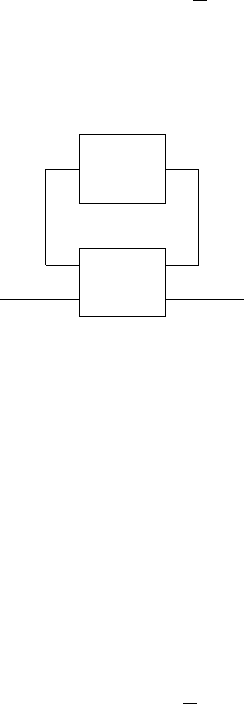
схемы, изображенной на рис. 8.4. Здесь G(s) — объект, который удобно представлять в

- -

Рис. 8.4: M–∆ конфигурация для задачи µ-синтеза.

виде блочной матрицы

G =

а C — регулятор; тогда

M = G

+ G

C(I − G

−1

= F

l(G,C),

где F

обозначает нижнее дробно-линейное преобразование (см. раздел 6.2). Таким об-

разом, задача свелась к выбору регулятора C, обеспечивающего выполнение условия

(G, C)

≤

а задача о максимальной робастности (т.е., о нахождении наибольшего γ, для которого

можно обеспечить робастную устойчивость) — к минимизации µ

(G, C)

по C:

min

(G, C)

К сожалению, прямые методы решения этой задачи неизвестны, и используется кос-

венный путь, не всегда гарантирующий нахождение решения. Вспомним, что для µ

известна верхняя граница (Теорема 58):

µ(M) ≤ inf

D∈D

kDMD

−1

8.6. Выводы 215

где D — блочно-диагональные матрицы той же структуры, что и ∆. При фиксирован-

ном D задача минимизации по C

min

kDF

(G, C)D

−1

∞

(8.15)

— это стандартная задача H

∞

-оптимизации (раздел 5.2), и для ее решения существуют

хорошо разработанные методы (использующие либо переход к пространству состояний

и уравнение Риккати, либо методы типа Неванлинны-Пика). С другой стороны, при

фиксированном C и ω решение задачи

min

D∈D

kDMD

−1

k, M = M(jω) = F

G(jω), C(jω)

может быть сведено к выпуклой конечномерной задаче оптимизации, для которой так-

же известны эффективные методы. Таким образом, в общих чертах метод решения

задачи µ-синтеза, называемый D– C итерациями , имеет следующий вид.

1. D-итерации: для найденного приближения C и сетки по частотам 0 < ω

< ω

. . . < ω

с помощью методов выпуклой минимизации решаются задачи

min

D∈D

kDM

−1

k, M

= M(jω

), i = 1, . . . , N,

решения которых обозначаются через D

. Затем находится функция D(s) ∈ RH

∞

D ∈ D, которая хорошо аппроксимирует найденные решения на сетке ω

: D(jω

) ≈

2. C-итерации: для найденного D(s), методами H

∞

-оптимизации решается задача (8.15)

и находится очередное приближение для регулятора C, после чего переходят к

пункту 1.

Нет нужды говорить, что каждый из пунктов алгоритма достаточно сложен и тре-

бует уточнения. Более того, в общей ситуации нет никакой гарантии, что в результате

удастся найти решение исходной задачи (8.15). Тем не менее, указанный подход реализо-

ван в пакете µ-Analysis and Synthesis Toolbox в системе Matlab и успешно применяется

для решения практических задач.

8.6 Выводы

• Задача стабилизации с помощью обратной связи, рассмотренная в Главе 4, может

быть обобщена на случай систем с неопределенностью (робастная стабилизация).

Для одномерного интервального объекта проблема стабилизации с помощью боль-

шого или малого коэффициента усиления решается для робастно минимально-

фазовых или робастно устойчивых систем (Теоремы 61 и 62). Для двухпарамет-

рических регуляторов робастная стабилизация проводится на основе робастного

D-разбиения. Однако в целом задача робастной стабилизации с помощью регуля-

торов низкого порядка не имеет простого решения.

216 Глава 8. Робастная стабилизация и управление

• Удобным аппаратом робастной стабилизации является техника, основанная на по-

строении общей кавадратичной функции Ляпунова. Так, для системы

˙x = A(q)x + Bu

с матрицей A, зависящей от параметров q ∈ Q, можно решить систему линейных

матричных неравенств

(q) + A(q)X − 2BB

< 0, q ∈ Q, X > 0,

и если ее решение X > 0 существует, то обратная связь u = −B

−1

x является

робастно стабилизирующей.

• Аналогичным образом, путем свед´ния к линейным матричным неравенствам, ре-

шается задача о гарантированном значении квадратичного показателя качества

для систем с параметрической неопределенностью (робастный линейно-квадра-

тичный регулятор).

• Результаты о робастной устойчивости при частотной неопределенности, приведен-

ные в разделе 7.3, сводят отыскание регулятора C(s), робастно стабилизирующего

объект, к решению неравенств типа

CSW

∞

≤

, S = (I + G

−1

(см. Теорему 56). Переходя к параметру Юлы Q в описании всех регуляторов C(s),

стабилизирующих номинальный объект G

(s), это неравенство переписывается в

форме

+ T

∞

≤

где матричные передаточные функции T

(s) легко вычисляются. Таким образом,

нахождение робастно стабилизирующего регулятора сводится к решению стан-

дартной задачи H

∞

-оптимизации и находится максимально допустимое γ, при

котором возможна робастная стабилизация.

Методы H

∞

-оптимизации могут быть использованы и в некоторых задачах робаст-

ной стабилизации при параметрической неопределенности в передаточных функ-

циях. Три примера иллюстрируют эффективность такого подхода: комплексные

параметры; дискретные системы с l

-неопределенностью; выпуклая параметриза-

ция при вещественной неопределенности.

• На основе µ-анализа (раздел 7.4) могут быть построены процедуры µ-синтеза.

Они сводятся к поочередной минимизации верхней грани для µ по регулятору C

и минимизации этой верхней грани при найденном C (D– C итерации). При этом,

однако, нет гарантии, что оптимальный максимально робастный регулятор будет

найден.

Глава 9

Нерешенные задачи

В данной главе мы обсудим некоторые важные задачи, допускающие простую фор-

мулировку, но эффективные методы решения которых неизвестны. Эти проблемы от-

носятся как к робастной теории, так и к классической теории линейных полностью

определенных систем. О многих из них уже упоминалось в предыдущих главах; там

обсуждались методы их решения в частных случаях.

9.1 Стабилизация регулятором заданной структуры

Рассмотрим простейший класс задач такого типа. Задан одномерный линейный объ-

ект

G(s) =

A(s)

B(s)

, A(s) = a

+ a

s + . . . + a

, B(s) = b

+ b

s + . . . + b

, m ≤ n;

можно ли его стабилизировать регулятором

C(s) =

N(s)

D(s)

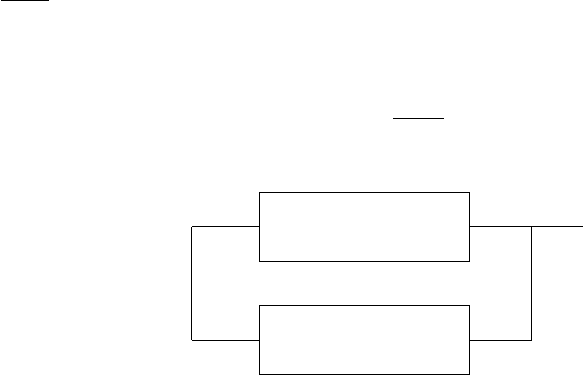
в цепи обратной связи (рис. 9.1), если порядки числителя и знаменателя регулятора

G(s) = A(s)/B(s)

C(s) = N(s)/D(s)

Рис. 9.1: Стабилизирующий регулятор заданной структуры.

не превосходят заданных чисел? С математической точки зрения вопрос сводится к

следующему: можно ли выбрать полиномы N(s), D(s) заданных порядков так, чтобы

характеристический полином

P (s) = A(s)N(s) + B(s)D(s)

217

218 Глава 9. Нерешенные задачи

был гурвицевым? Если отказаться от условия ограниченности порядка регулятора, то

полное решение задачи было приведено в разделе 4.2: стабилизация всегда возможна,

если A (s) и B(s) не имеют общих неустойчивых корней. В разделе 4.1 приводились

различные ситуации, когда стабилизация заведомо возможна с помощью простого ко-

эффициента усиления C(s) = k (это случаи устойчивого или минимальнофазового объ-

екта). Обсуждался также случай, когда регулятор C(s) содержит лишь два параметра

(например, является ПИ-регулятором); здесь полное решение проблемы возможно най-

ти с помощью D-разбиения. Однако, что происходит в общем случае, когда регулятор

содержит ` > 2 параметров? Если представить N(s), D(s) в виде

N(s) = q

+ . . . + q

k−1

, D(s) = 1 + q

k+1

s + . . . + q

`−k

где k, ` заданы, то задача сводится к проверке, существует ли в аффинном семействе

полиномов

P(s, Q) =

P (s, q) = P

(s) +

i=1

(s), q ∈ R

, (9.1)

устойчивый полином. Здесь

(s) = B(s), P

(s) = s

i−1

A(s), i = 1, . . . , k, P

(s) = s

i−k

B(s), i = k + 1, . . . , `.

Если задавать структуру регулятора иначе (например, ПИД-регулятор вида C(s) = q

/s+q

s), то задача вновь сведется к проблеме (9.1). Таким образом, общей схемой для

исследования вопроса стабилизируемости регуляторами заданной структуры является

Проблема 1. Существует ли в аффинном семействе (9.1) хотя бы один устойчивый

полином?

Можно предположить, что на параметры регулятора наложены некоторые ограни-

чения

q ∈ Q. (9.2)

Например, это могут быть интервальные ограничения:

= {q ∈ R

: q

≤ q

, i = 1, . . . , `} (9.3)

или ограничения на близость q к номинальному значению q

в какой либо норме:

= {q ∈ R

: |q − q

| ≤ γ}; (9.4)

тогда получаем ограниченный вариант Проблемы 1:

Проблема 2. Существует ли в семействе (9.1)–(9.2) хотя бы один устойчивый по-

лином?

На первый взгляд, Проблема 2 очень близка к задаче о робастной устойчивости поли-

номов, эффективные методы решения которой были описаны в разделе 7.1. Единствен-

ная разница в том, что в задаче о робастной устойчивости речь шла о существовании

хотя бы одного неустойчивого полинома в семействе (9.1)–(9.2), тогда как в Пробле-

ме 2 ищется хотя бы один устойчивый полином в том же семействе. Эта на первый

9.1. Стабилизация регулятором заданной структуры 219

взгляд незначительная разница приводит к кардинальной перемене в сложности зада-

чи. Оказывается, Проблема 2 является NP -сложной, причем даже в простейших слу-

чаях, таких как поиск устойчивого полинома в интервальном семействе. Поэтому для

нее не существует методов решения полиномиальной сложности (т.е. таких, в которых

число операций полиномиально зависит от степени полинома P (s, q)). Более того, для

таких задач неверны и результаты типа теоремы Харитонова или реберной теоремы

(см. раздел 7.1). Иначе говоря, все вершины и все ребра многогранника Q могут быть

неустойчивы, однако некоторому q ∈ Q может соответствовать устойчивый полином.

Разумеется, можно предложить некоторые достаточные условия, которые гарантируют

положительный или отрицательный ответ в Проблеме 2. Однако эти условия далеки от

необходимых.

Другим возможным путем решения мог бы быть вероятностный подход, который

применялся в разделе 7.5 к задаче о робастной устойчивости. Так, можно попытаться

генерировать случайные точки q

из Q и проверять на устойчивость полиномы P (s, q

Однако эффективность такого подхода невелика — обычно устойчивые полиномы в

семействе P(s, Q), даже если они существуют, составляют очень небольшую по объему

долю. Например, в интервальном семействе полиномов степени n с коэффициентами

между 0 и 1 доля устойчивых полиномов v(n) оценивется как

v(n) ≤

[(n + 1)/2]!

(хотя эта оценка сильно завышена) или асимптотически v(n) ≈ e

−Cn

, где C — некото-

рая константа; для n = 10 численное моделирование дает v(n) ≈ 10

−9

. Таким образом,

вероятность получить устойчивый полином степени 10 при случайной генерации коэф-

фициентов, равномерно распределенных на [0, 1], ничтожно мала.

Существуют и численные методы решения Проблемы 2. Введем функцию

η(q)

= max

Re s

(q),

где s

(q) — корни полинома P (s, q). Ясно, что для устойчивого полинома имеем η(q) < 0,

а для неустойчивых η(q) ≥ 0. Поэтому можно решать задачу

min

q∈Q

η(q). (9.5)

Функция η(q) — дифференцируемая, если все s

(q) различны; с помощью теории воз-

мущений (см. раздел 10 Приложения и обсуждение в разделе 7.2) нетрудно выписать

ее градиент в таких точках. После этого естественно применить метод типа проекции

градиента для решения задачи оптимизации (9.5). К сожалению, такой подход не га-

рантирует получения правильного ответа в Проблеме 2. Дело в том, что функция η(q)

— невыпуклая, и метод может привести к локальному (а не глобальному) минимуму.

Кроме того, дополнительные трудности возникают в случае кратных корней. При этом

искомый устойчивый полином, возможно, не будет найден, хотя он и существует.

Этим же недостатком обладают численные методы, основанные на использовании

алгебраических критериев устойчивости типа Рауса-Гурвица. Именно, будем опериро-

вать с полиномом P (s, q) с помощью алгоритма Рауса, проводя вычисления в анали-

тической форме (например, с помощью пакета Symbolic Math Toolbox для символьных

220 Глава 9. Нерешенные задачи

вычислений в системе Matlab). Тогда условие положительности элементов первого

столбца таблицы Рауса примет вид

(q) > 0, i = 1, . . . , n, q ∈ Q. (9.6)

Таким образом, проверка наличия устойчивого полинома в семействе сводится к выяс-

нению разрешимости системы неравенств (9.6). Однако методы решения таких невы-

пуклых неравенств очень сложны.

Таким образом, эффективные методы решения Проблем 1 и 2, гарантирующие по-

лучение точного ответа в общей ситуации, в настоящее время неизвестны. Заметим еще,

что Проблема 2 в частном случае (когда q

являются коэффициентами P (s, q)) может

быть записана в следующей форме.

Проблема 3. Дан неустойчивый полином P

(s). Найти ближайший устойчивый по-

лином той же степени.

Здесь расстояние между полиномами A(s) = a

+ a

s + . . . + a

и B(s) = b

+ b

s +

. . . + b

понимается как dist (A, B) = |a −b|, где a, b ∈ R

n+1

— векторы коэффициентов

A(s), B(s), а |·| — некоторая норма в R

n+1

, например, |a −b| = max

−b

| или |a −b| =

i=1

− b

)

1/2

. Тогда, если

min

P (s,q)∈P

dist

(s), P (s, q)

= γ

∗

≤ γ,

где P — множество устойчивых полиномов, то решение Проблемы 2 с Q вида (9.4) и

P (s, q) = q

s+. . .+q

существует; в противном случае — не существует. Вновь Про-

блема 3 получается перестановкой терминов “устойчивый” и “неустойчивый” в простой

задаче об отыскании радиуса устойчивости полинома. Однако эта замена принципиаль-

но усложняет задачу.

До сих пор мы рассматривали одномерные задачи, описываемые с помощью скаляр-

ных передаточных функций. Однако совершенно аналогичный круг трудных проблем

возникает при описании систем в пространстве состояний. Типичной является задача

о статическом регуляторе по выходу: для системы

˙x = Ax + Bu, y = Cx,

выяснить, можно ли ее стабилизировать обратной связью вида

u = Ky.

Алгебраическая формулировка той же задачи: существует ли матрица K такая, что

при данных A, B, C матрица A

= A + BKC устойчива. Рассматривая элементы матри-

цы K как параметры q, заключаем, что задача о статической стабилизации по выходу,

является частным случаем более общей проблемы.

Проблема 4. Дано аффинное семейство матриц

A(q) = A

i=1

, q ∈ R

, (9.7)