Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. т а ін. Вища математика у прикладах та задачах. Ч 3
Подождите немного. Документ загружается.


§3.
Ряди Фур'є
241
-Зтс
-2л -тс О
Л
/
2л
Зтс
4тс 5тс х
Рис.2.2
Задана функція задовольняє умови теореми Діріхле. Знайдемо коефі-
цієнти Фур'є. Використовуючи властивість адитивності визначеного інтег-
рала, матимемо
І
« ] 0 ]
тс
]х
2
=
—
\/(х)ах
=
—
\0ах-\—\хах
=
тг-
1
тг і тг-
1
Я 2
Я
2"
-тс -тс 0
Далі для обчислення коефіцієнтів
а
п
та Ь
п
використовуємо інтегру-
вання частинами:
або безпосередньо використовуємо формули інтегрування, наведені
на
по-
чатку даного пункту.
а„
=
—
^хсо5пхсіх
=
—
51П
ПХ
тс і и
—
ГЇІПИХЛ
-С08ИХ
яя
С05ЯЯ-1
(-1)"-1
ия
ял
Отже,
2
——
, « -
непарне,
я
я
0,
п -
парне.
а
2и=°>
«2«-1
(2и-1)я
(
іТС
«тс/ \ї/ „ тс . л
1г. , 1 Г ,1
С05ИХ
\ 1
ХС08ИХ
1 г
Ь„
=
—
\х&тпхах =
—
\ха\ =
+
—
\со5пхах
К
п
і І
л
;
л
1
п
о «і
С05ИЯ
(-1)
п+1
242
Глава 2. Ряди
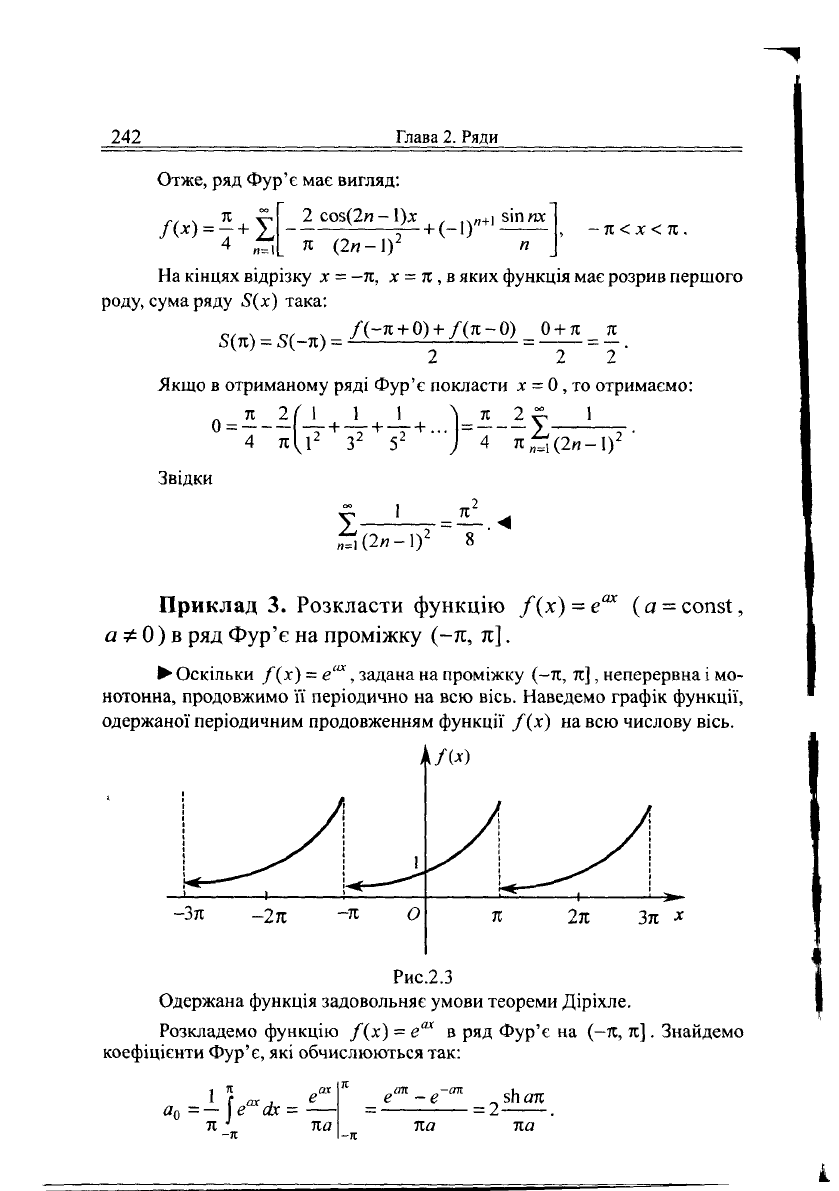
Отже,
ряд Фур'є має вигляд:
/00
= 7+1
2 соз(2и - 1)х
+
^ ^„+| зіпих
•
Л
< X <
7Х
.
л (2«-1Г
На кінцях відрізку х = -л, х = я , в яких функція має розрив першого
роду, сума ряду 5(х) така:
/(-я + 0) + /(я-0) _ 0 + л _ я
2 '
5(я) = 5(-л) =
•
2 2
Якщо в отриманому ряді Фур'є покласти х = 0, то отримаємо:
„ я 2М 1 1 ^ л 2 і
4 лі 1
4 я
и=
і(2и-І)
2
'
Звідки
00
1
_ і
V —
й
^(2л7-1)
2
~Т
Приклад
3. Розкласти функцію /(х) = е
ах
(а = сопзІ,
а Ф
0) в ряд Фур'є на проміжку (-я, ті].
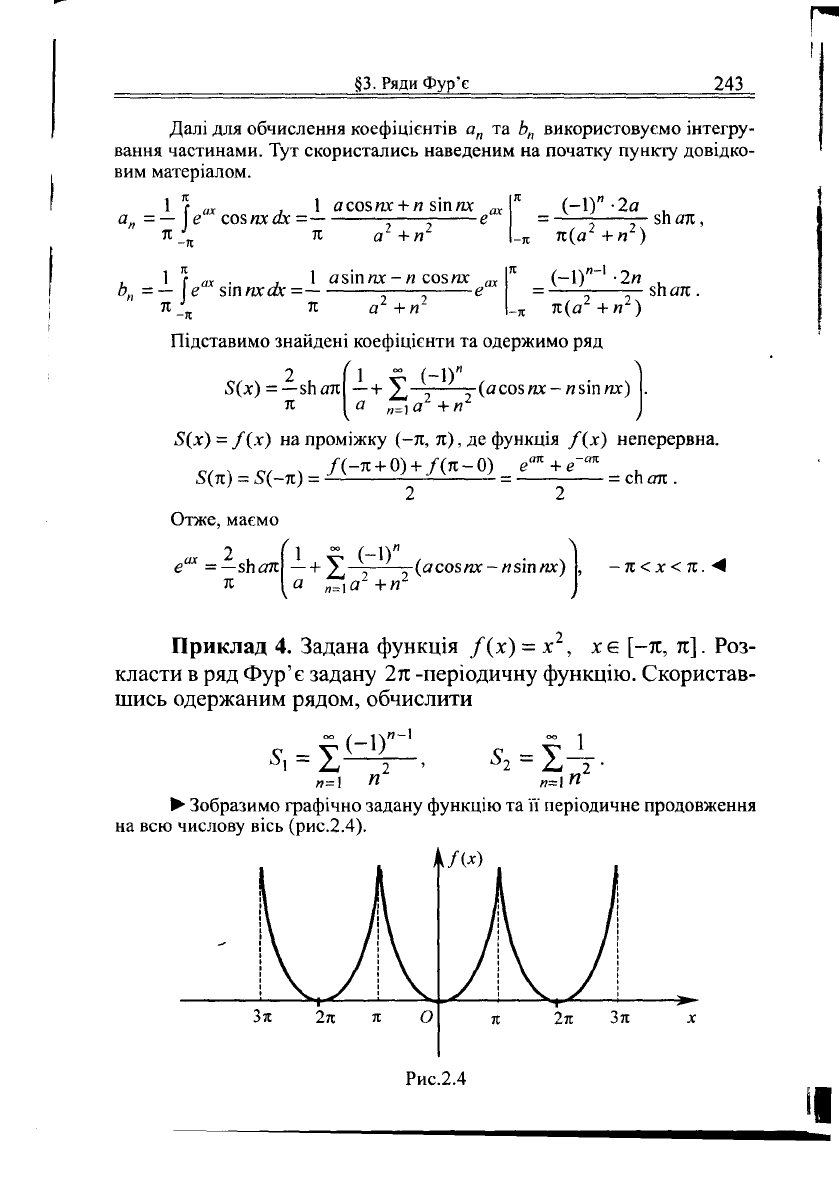
•
Оскільки /(х) = е
т
, задана на проміжку (-я, л], неперервна і мо-
нотонна, продовжимо її періодично на всю вісь. Наведемо графік функції,
одержаної періодичним продовженням функції /(х) на всю числову вісь.
1
\/(х)
-Зл -2л -я 0
Рис
п
2л Зя х
2.3
Одержана функція задовольняє умови теореми Діріхле.
Розкладемо функцію /(х) = е
ах
в ряд Фур'є на (-я, я]. Знайдемо
коефіцієнти Фур'є, які обчислюються так:
§3.
Ряди Фур'є
243
Далі
для
обчислення коефіцієнтів
ап та Ьп
використовуємо інтегру-
вання частинами.
Тут
скористались наведеним
на
початку пункту довідко-
вим матеріалом.
(-\)"-2а
1
Г ах .1
СІС05ПХ
+
П
5ІПЛХ
ап=—\е
со$пхах=
; ; е~
а
2
+п
2
,
1 г „ . , 1
азіплх-/?
соз гаг
Ьп=—
\е
$тпхах
= ; --е~
2
2
а
+п
-п п(а
2
+п
2
)
'
=
(-1)"''
2и
-я к(а
2
+п
2
)
зЬал,
зпая.
Підставимо знайдені коефіцієнти
та
одержимо
ряд
5(х)
=
— зЬая
тс
(-1)"
1
а „
=1
а
2
+и
2
(асозих-изіпях)
5(х)
= /(х) на
проміжку
(-тс, я), де
функція
/(х)
неперервна.
^^(-^^^^^^-^^"^""^сЬатс.
Отже, маємо
е
ах
=-$Ьаж
тс
(-1)"
а ^а
2
+п
2
(<зсо5«х-«зіп«х)
-я<х<я.
Приклад
4.
Задана функція
/(х)= х
2
, х є [-тс,
тс]. Роз-
класти
в
ряд Фур'є задану 2тс -періодичну функцію. Скористав-
шись одержаним рядом, обчислити
(-1>
л-1
5
2
= Х
1
• Зобразимо графічно задану функцію
та її
періодичне продовження
на
всю
числову вісь (рис.2.4).
VI
к/(х)
\)
Зтс
2тс я О
я
2я Зя х
Рис.2.4

244
Глава 2 Ряди
У даному випадку /(х) - парна функція, тому Ьп = 0, V/?.
а0
=-\/(х)ах=—
\х
2
ах = ^-~.
п
о
п
о
3
Для обчислення коефіцієнтів а„ скористаємось двічі інтегруванням
частинами. Можливо також використання формул інтегрування, наведених
на початку даного пункту.
2 2 2
ап -— І/(х)созпхах = — [х
2
созлхах = —
2 51ПЛХ
тс 2
%
\
1
хзіп гас ах
о "о
х соз пх 1 .
у
—— зіп пх
=
-тНГ.
о п
Періодичне продовження /(х) на всю числову вісь є неперервною
функцією, бо /(—тс + 0) = /(тс - 0) = тс
2
. Виконуються умови теореми Діріх-
ле.
Підставимо коефіцієнти в ряд Фур'є. Маємо:
тс
2
°° (—IV
й
5(х) = — + 4 ^ созих,
3
п=1 П
де 5(х) = /(х) = х для всіх х, бо функція /(х) неперервна у всіх точках.
Отже,
2 ТС , ^ (~П
х =— + 4
2,—і—
со$пх,
-я<х<л.
3
/1=1 п
При х = 0 маємо:
тобто
тобто
(-0
я-1
Я _ ^
(-1>
12 ,^ «
2
При х = тс маємо:
я-1
(-1)"-' л
2
/1=1
я
12
2 _
71
Л =

§3,
Ряди Фур'є
245
Приклад 5. Розкласти функцію /(х) = х в ряд Фур'є на
проміжку
(-7С,
я).
• Наведемо графік заданої функції /(х) = х на проміжку (-тс, тс) та
її періодичне продовження на всю числову вісь (рис.2.5).
Рис.2.5
Функція /(х) обмежена та має обмежену похідну, тому її ряд Фур'є
у точках неперервності збігатиметься до цієї функції (теорема Діріхле).
Знайдемо коефіцієнти Фур'є. Оскільки функція /(*) = х - непарна,
то а
0
= 0, а
п
= 0 Уп .
2
тс
2 (
к
^
Ь
п
= — \х$'тпхах =
хсоьпхІ?
-\со$пхах
п
о
™{ о
2
(
_
іГ
-і
п
Підставимо одержані коефіцієнти та отримаємо ряд Фур'є, сума 8{х)
якого така:
£(
х
)
=
$іппхах = 2 X зіпих.
я=1
и=1
П
Згідно з теоремою Діріхле
£(*) = /(*) = х, хе (—тс, тс),
Отже,
•
Н)
«-1
х = 2І-
и
=і »
зіп пх, хе (—тс, тс).
Приклад 6. Розкласти функцію /(х) =
тс
- х, 0 < х < тс в
ряд Фур'є: а) по косинусах; б) по синусах.

246
Глава 2. Ряди
• Задана функція при її парному та непарному продовженнях на відрі-
зок [—я, 0] буде кусково-гладкою, тобто задовольняє умови теореми Діріхле.
Розглядаємо ці два вказані способи продовження функції, тоді матимемо від-
повідно розкладання функції в ряд по косинусах та по синусах.
а) розкладання в ряд Фур'є по косинусах.
Продовжимо функцію /(х) = л-х на відрізок
[-тс,0]
парним чином
та періодично продовжимо отриману функцію на всю числову вісь (рис.2.6).
-371 -2л -я О
2л Зл х
Рис.2.6
Тоді ряд Фур'є для цієї функції матиме вигляд:
Я
х
)
= ~+1
а
п
СО&ПХ,
2
И
=1
де коефіцієнти Фур'є визначаються так:
= — Г(л-х)ох = —(л-х)
2
пі п
2 г. , , 2 г /зіп пх
а
п
=—\(я-х)созихах =— (л-х)а
ЗІП ЛХ
пп
(л-х)
-[1-(-1)"]=
ж і ге
0 "о
4
^ь'тпхсіх
пп
-созпх
-(1-созшс) =
о пп
—, п - непарне,
пп
0, п — парне.
Отже,

§3.
Ряди
Фур'є
247
Тоді
я 4 (созх созЗх соз5х ^
л
_ _
я-х=
— + — —— +—— + —г—+
... , 0<х<л
2 л( І
2
З
2
5
2
)
або
я 4 соз(2/7-1)х
2 л~
(2/7-І)
2
0<х< я.
б) розкладання в ряд Фур'є по синусах.
Продовжимо функцію /(х) = я - х на відрізок [-я, 0] непарним чи-
ном та періодично продовжимо отриману функцію на всю числову вісь
(рис.2.7).
1
.
л
N.
-2л | \ О
>У 2тс
\^
4л
-Зя\.
;
_я
^ч
я\
-я X
Рис.2.7
ЗлЧ
ч
X
Тоді ряд Фур'є для цієї функції матиме вигляд:
де коефіцієнти Фур'є:
або
/(х)
=
У
і
Ь„$тпх,
Ь
п
= — \(к-х)$тжах=—\(п-х)сі\-
с0&пх
|
=
Я
Ь
к
о V » )
1
к
І
С05ИХЯХ
тг
*
(л-х)
о
С05/7Х
0
"•о
2 я 2
= -, п =
1,2,...
я п п
Отже,
.(зіпх зіп2х зіпЗх ^
я-х = 2 + + +... , 0<х<л
1
1 2 З У
л-х = 2 ]Г
51П/7Х
0<Х<Я.
248
Глава
2.
Ряди
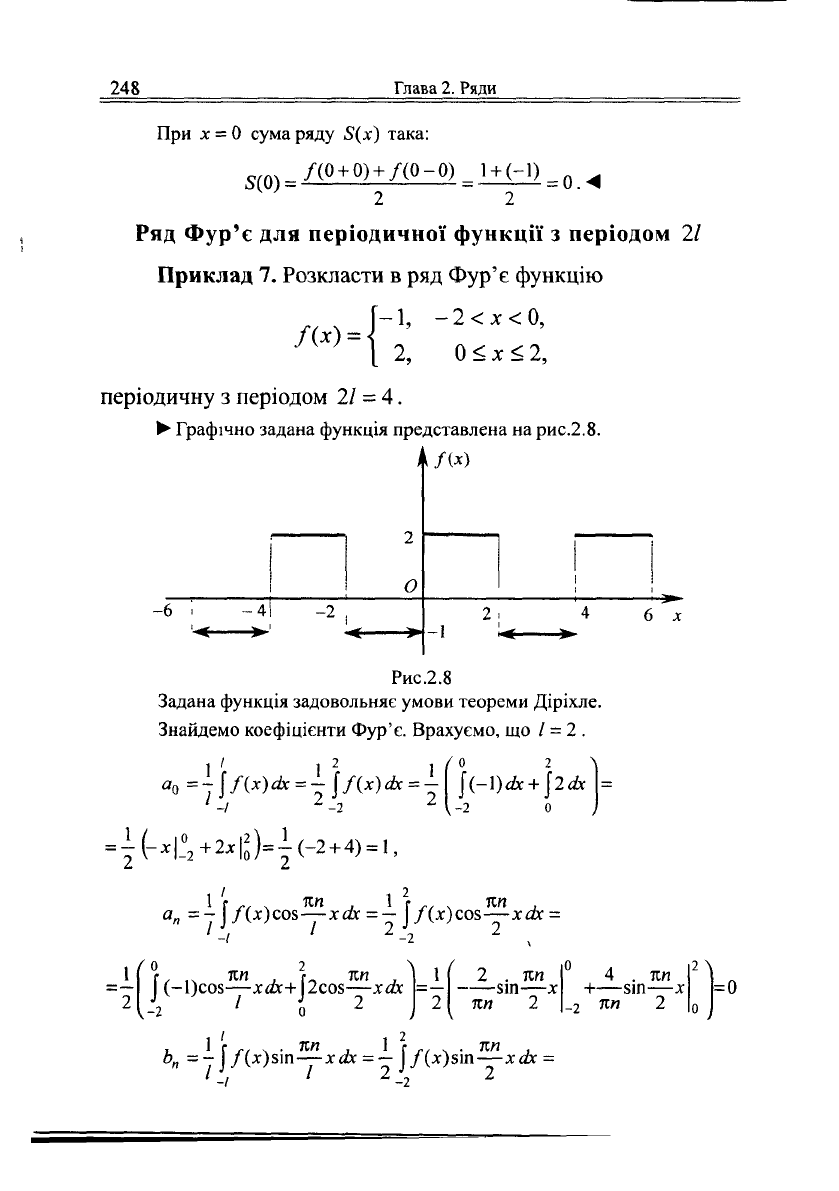
При
х = 0
сума ряду
5(х)
така:
5(0) =
/(о+о)+ЯО-о)
=
і + Н)
= 0
л
2
2
Ряд Фур'є
для
періодичної функції
з
періодом
21
Приклад
7.
Розкласти
в ряд
Фур'є функцію
•1,
-2 < х
<
0,
Ах)
=
2, 0<х<2,
періодичну
з
періодом 21
= 4.
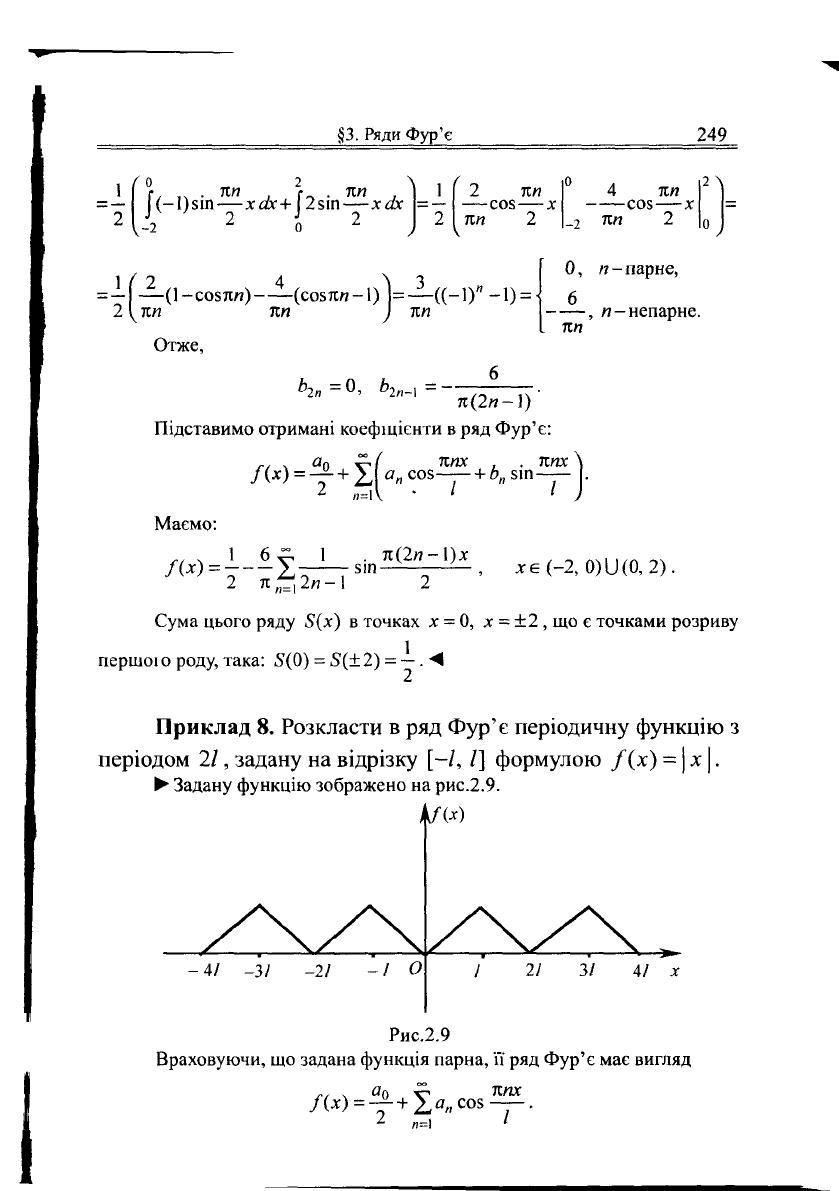
• Графічно задана функція представлена
на
рис.2.8.
і \
/(*)
-6
і -41
-2
1
Рис.2.8
Задана функція задовольняє умови теореми Діріхле
Знайдемо коефіцієнти Фур'є. Врахуємо,
що
1
= 2.
1
' 1
2
1 (° 2 \
а
0
=-\Пх)ах = -ІЯх)ах = - \(-\)ах + \2ах
-І -2 1-2 0
±(-х£
2+
2х\і)Л(-2
+
4)
=
1,
1
' 1
2
а
п
=у
|/(х)соз—хат
=—
|/(х)соз—хах
=
2
,ч
ЇСИ і г„ тси
^ (-І)соз—хах+рсоз—хах
ї
о
о
1
^ 1
2
Ь„
= - І
/їх)зіп—хсіх-—
Г
/їх)зіп—хат
:
п
7
у V
;
2^/ 2
2
. тси
ЗІП
X
тси
2
6
х
4
. тси
Н ЗІП—X
2
тси 2
=0
§3.
Ряди Фур'є
249
1
1
2 пп
~ —
—соз—X
2
)
пп 2
(
0 _ 2
Г.
. ПП , г . ПП ,
^
(-І)зт — хах+\ 2 зіп—хах
:-(—(1
-созтси)-—
(соз
ял-1)1=
—((-1)" -1) =
2 І ял пп ) пп
Отже,
4 пп
соз—х
2
пп 2
0, «-парне,
,
п-непарне.
пп
Я(2«-1)
Підставимо отримані коефіцієнти в ряд Фур'є:
г,
ч
а
о яга і • яга:
/(*) = -^-+ П
а
п соз—- +
ЗІП
—
2 „=1\. • * '
Маємо:
2 я " 2л -
1
.
тс(2л - \)х , _
лч
. , ,„ _
ч
зіп—
— , хе (-2, 0)1)(0, 2).
Сума цього ряду 5(х) в точках х = 0, х = ±2 , що є точками розриву
першою роду, така: 5(0) = 5(±2) = —. А
Приклад
8. Розкласти в ряд Фур'є періодичну функцію з
періодом
21, задану на відрізку [-/, /] формулою Дх) =
|
х
|.
•
Задану функцію зображено на рис.2.9.
У(х)
41 -3/ -21 -1 О 21 3/ 4/ х
Рис.2.9
Враховуючи, що задана функція парна, її ряд Фур'є має вигляд

250
Глава 2. Ряди
Знаходимо коефіцієнти а
0
та а„, п =
1,2,...
2
і
2
і
а
о ~-\і(х)ах = -\хах = 1,
'о
'о
2
Г
/V \
пп
^
2
Г
ш
л
2
Г
./
1
•
к
>
а„ =
—
/(х)соз—хах = — хсоз—хах = — ха — зіп —
2 \ ,( . кп ) 2
=
—
\ха
зіп—х =—
тс«о
^ / ) пп
хзіп X
/
- І зіп—хах
0 о
1
2 І пп
СОЗ X
пп пп І
21
(с057Ш-1)
= -^((-ГГ-1) =
~2„2
П П
2 2
тсп
Отже,
а
2» = °> «2/1-1 = •
0, п
—
парне,
41
, п - непарне.
тс п
41
(2п-\)
2
п
2
Підставивши знайдені значення коефіцієнтів в ряд Фур'є, отримаємо
1 л(2и-1)х
II
1 41
V
2 к
2
~(2«-1)
2
-соз-
, -1<х<1.<
Приклад 9. Розкласти функцію /(х) = х
—
— , задану на
відрізку
[0,2],
в ряд Фур'є: а) по косинусах; б) по синусах.
• а) розкладання в ряд Фур'є по косинусах.
2
X
Продовжимо функцію /(х) = х—— на відрізок
[-2,0]
парним чи-
ном. Маємо / = 2 . Одержану функцію продовжимо на всю числову вісь з
періодом Г = 2/ = 4 (рис.2.10).
Л/І.Х)
1/2
-4 -І О
Рис.2.10
