Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. т а ін. Вища математика у прикладах та задачах. Ч 3

Подождите немного. Документ загружается.

Комплексні числа

271

ІІ^Ле'^іЧ*),

"=г"е"".

Ця

формула

формулою Муавра

для

випадку задання комплексного

числа

показниковій формі.

л/7

^7е

, к =

0,п~].

Тут

=Г]

е'

Фі

е'

Ф2

2 =

ге'

//.

Контрольні питання

та

завдання

Дайте означення комплексного числа; що таке дійсна

та

уявна частина комплексного числа?

Як

визначається уявна одиниця?

Які комплексні числа називаються рівними; спряженими?

Як

зображується комплексне число

на

площині?

Яка

форма запису комплексного числа називається

ал-

гебраїчною; тригонометричною?

6. Дайте означення модуля та аргументу комплексного числа.

Що

називають головним значенням аргументу?

За

якою формулою визначається модуль комплексного

числа, аргумент комплексного числа?

Як

виконуються

дії

над комплексними числами, задани-

ми

алгебраїчній формі?

10.

Як

виконуються дії над комплексними числами, задани-

ми

тригонометричній формі?

11.

Наведіть показникову форму комплексного числа.

12.

Як

виконуються

дії

над комплексними числами, задани-

ми

показниковій формі?

13.

Який геометричний зміст суми

та

різниці комплексних

чисел?

14.

Який геометричний зміст операції множення двох комп-

лексних чисел?

272

Глава 3. Функції комплексної змінної

15.

Який геометричний зміст операції ділення двох комплекс-

них чисел?

///. Приклади розв'язання задач

Приклад 1. Задано комплексні числа

=-3 + 2/,

=2-3/.

Виконати вказані дії над ними.

а) 2, +г

; б) 2,-г

;

в)г

; г)-^-;

д,2,

• а) 2, +2

= (-3 + 2/) + (2-3/) = (-3 + 2) + (2-3)/ =

-1-/;

б) 2, -2

=(-3 + 2/)-(2-3/) = (-3-2) +(2 + 3)/=-5 +5/;

в) 2, -2

= (-3 + 2і)• (2-30 = -3-2-2(-3) + ((-ЗХ-3) + 2• 2)і = 13і;

г) для знаходження частки чисельник та знаменник домножимо на

вираз,

спряжений знаменнику

_-3 + 2/_(-3 + 2/)(2 + 3/)_(-3-2-2-3) + (-3-3 + 2-2)/_ 12 5..

~ 2-3/ ~ (2-3/)(2 + 3/) ~ 4 + 9 ~ 13 ІЗ*'

д)

і\

= (-3 + 2 О

= (-3)

+ 3

•

(-3)

•

2і + 3

•

(-3)

•

(2/)

+ (2 і)

= -27+ 54/ +36-8/= 9 +46/.-І

Приклад 2. Задано комплексні числа г, =

-2/, г

=2+/,

= 5/. Знайти 2 = 2

•

+ г

• Знаходимо

=(2+і)

= 4 + 4/ + /

= 4 + 4/-1 = 3 + 4/,

-2

=(1-2/)(3 + 40 = (3 + 8) + (4-6)/ = 11-2/.

Тоді

2 = 2, -2

=(11 -2/) + 5/ = 11+3/.««

Приклад 3. Знайти дійсні розв'язки рівняння

(4 + 2/)х + (5-3/)^ = 13+/.

Комплексні числа

273

• Перетворимо рівняння, виділивши в його лівій частині дійсну та

уявну частини:

(Ах + 5у) + і(2х - Зу) = 13 + і.

Звідси згідно з означенням рівності двох комплексних чисел, отрима-

ємо систему рівнянь

Г4х + 5у = 13,

[2х - 3^ = 1.

Розв'язавши систему, отримаємо х = 2, у = 1.

Отже, дійсний розв'язок заданого рівняння х = 2, у = 1. ^

Приклад 4. Для заданого комплексного числа і знайти

Ке2,\тг

- дійсну та уявну частини, \г\, ащг - модуль та го-

ловне значення аргументу; записати ці числа в тригонометрич-

ній та показниковій формі; зобразити ці числа на комплексній

площині.

а) 2 =

+ /; б) 2 = -2 + 2л/Зг;

в)2

= -1-/73; г)г = 2л/3-2/.

• а) 2 =

+ /'.

Маємо: Ке2 = х = 1,

ІШ2

= _у = 1.

На комплексній площині цьому числу відповідає точка М(\,1)

(рис.3.3а).

\=г =

4х

+у

=Л/Г+Т = Л/2.

г§ ф = — = 1, точка М(\, 1)є І чверті, тоді згідно з формулою (3.6)

маємо: ф = аг§ г = агсі§ 1 = —.

Тригонометрична форма: 2 = -І2 ^соз —+ і зіп ^ ^.

Показникова форма: 2 =

б) 2 = -2 +

2л/3/.

Маємо: Ке 2 = х = -2 , Іт 2 = у = 2л/з .

На комплексній площині цьому числу відповідає точка М(-2, 2л/3)

(рис.3.36).

|=г =

/д:

=>/(-2)

+(2л/3)

=7Ї6=4.

274

Глава

Функції комплексної змінної

і£

—

= -

_^/з

точка

М(-2,

2л/з~)

є II

чверті, тоді згідно

-2

формулою

(3.6)

маємо:

ф =

аг

тс

агс

І8

(-ТІ) =

-= -|.

Тригонометрична форма:

2 = 4 |соз +1 зіп —^

2к

—

Показникова форма:

2 = 4 е

а)

б)

Рис.3.3

в)

г =

-1-/\/з

Маємо:

Ке2 = х =

-1,

Іш 2 = у = - л/з.

На комплексній площині цьому числу відповідає точка

М(—\,— VI)

(рис.3.4а).

;\=г

4х

+у

л/С-О

+(-

VI)

=74=2.

І8Ф

= ~

= 7з~ ,

точка

М(-\,- л/з)є III

чверті, тоді згідно

2я

формулою

(3.6)

маємо:

ф = аг§2 = -тс + агсі§л/з = -л + -у

Тригонометрична форма:

2 = 2 ^соз ^- ^ |+ / зіп

т)}

Показникова форма:

г = 2 е

г)

2 =

2л/3-2і.

Маємо:

Яе г = х = 2-Уз , Іт 2 = у = - 2 .

На комплексній площині цьому числу відповідає точка

М(2л/з, - 2)

(рис.3.4б).

§ 1. Комплексні числа

275

\г\=г = 4х

+ у

=7(2 л/3)

+(-2)

=Л/Ї6=4.

у - 2 1 г-

г§ ф = — = —= = =, точка М(2^3, - 2) є IV чверті, тоді згідно

х 2лІЗ л/З

з формулою (3.6) маємо: ф =

аг§2

= агсі§

(

Гз

тс

Тригонометрична форма: г = 4 | соз |

—

-1-7

зіп

—

Показникова форма: 2 = 4 е

2л/з

>*ф х

-2

б) а)

Рис.3.4

Зауважимо, що перехід до тригонометричної форми можна проводи-

ти,

виконавши деякі перетворення заданого числа г = х + іу, звівши його

до такого вигляду, щоб можна було формально замінити х та у на созф та

зіп ф відповідно. Для цього знаходимо

121,

домножуємо та ділимо на нього

задане число.

Виконаємо такі перетворення над заданими числами.

а) 2 =

+ /'.

|2|

= л/2\

+ / = л/2

-4= + /

-4= |= -І2 {соз

—

+ /зіп

—

{42 42) { 4 4

б) 2 = -2 + 2л/з/.

1-1

= 4,

-2 +

2л/3/'

= 4

2 .2л/з

—+/

4 4

= 4

1 .VI

—+і

2 2

2тс . . 2тс

= 4 соз (-/зіп—

З З

276

Глава 3. Функції комплексної змінної

ґ (

= 2 соз

2 ' 2

2тс

+ / зіп

2л

В)

2 =

-1-л/3/.

1-1

= 2,

= -1-л/3/=2

г) 2 = 2л/з-2/.

1-1

= 4,

= 2л/3-2/ = 4

б; ^6

Геометричну ілюстрацію цих результатів наведено на рис.3.3, рис.3.4. М

Приклад 5. Знайти дійсну та уявну частини комплексних

2-/з

—

4 4 2 2

= 4| созі -— )+/'зіп(-— ^

чисел.

а) 2--

В)

2 =

1-І

б) 2 =

1-І

1+1

1_.

л/3

2 ' 2

Г) 2 =

Ґ2 + і^

І + і

• Для знаходження дійсної та уявної частини комплексного числа 2

представимо його в алгебраїчній формі: г = х + іу. Тоді дійсна частина

Ке 2 = х, а уявна частина Іт 2 = у .

а) 2 =

1-/

Для запису даного числа в алгебраїчній формі домножимо чисельник

та знаменник на вираз, спряжений знаменнику:

1 _ 1(1 + /) _! + '"_! !•

~ 1-/~ (1-/)(1 + 0 ~

~ 2 2

Отже,

Р.Є2

Іт 2 = —.

б) 2 =

1-і

+ /

Для запису даного числа в алгебраїчній формі домножимо чисельник

та знаменник на вираз, спряжений знаменнику, та піднесемо до третього

степеня:

§ 1. Комплексні числа

277

_ Го-оа-о

(1+0(1-0

Отже, Ке 2 = 0 , Іт 2 = 1

1-2/-1

В) 2 =

2 ' 2

л/з~

Запишемо число 2, =

—

- / в тригонометричній формі, а потім

піднесемо його до третього степеня, використовуючи формулу Муавра. Вра-

ховуючи, що 12) (= г = 1, аг§

= - у, маємо

2 = | —-/

2 2

тс

\ . . С тс

СОБ + /51П

З ІЗ

С05(-л)

+ /ЗІП(-ТС)

= СО5ТС-/'ЗІПТС = -1 + 0 = -1 .

Отже, Ке2 = -1, Іт2 = 0.

7 4- ґ

Г) 2 =

2 + і

;19

+ /

Враховуючи, що /' =-1, і = 1, маємо і = /, / = -/'.Тоді

2 =

ті

2 + і

1-і

^(2 + 00 + ОУ /Ч2-1) + Зі

ч2

1+3*

/, с- глч ^ 3 .

=-(1+6/-9) = -2 + -/.

2 4 2

Отже, Ке 2 = -2 , Іт г = —. *4

Приклад 6. Знайти модулі, головні значення аргументів

та аргументи заданих комплексних чисел.

\ і .123 Ґ-\ К . . К

а) 2 = 1+; : о) 2 = -соз—+/зіп—.

7 7

• Запишемо задані числа у тригонометричній формі, звідки знайде-

мо модулі та аргументи цих комплексних чисел.

а)2 =

+ /

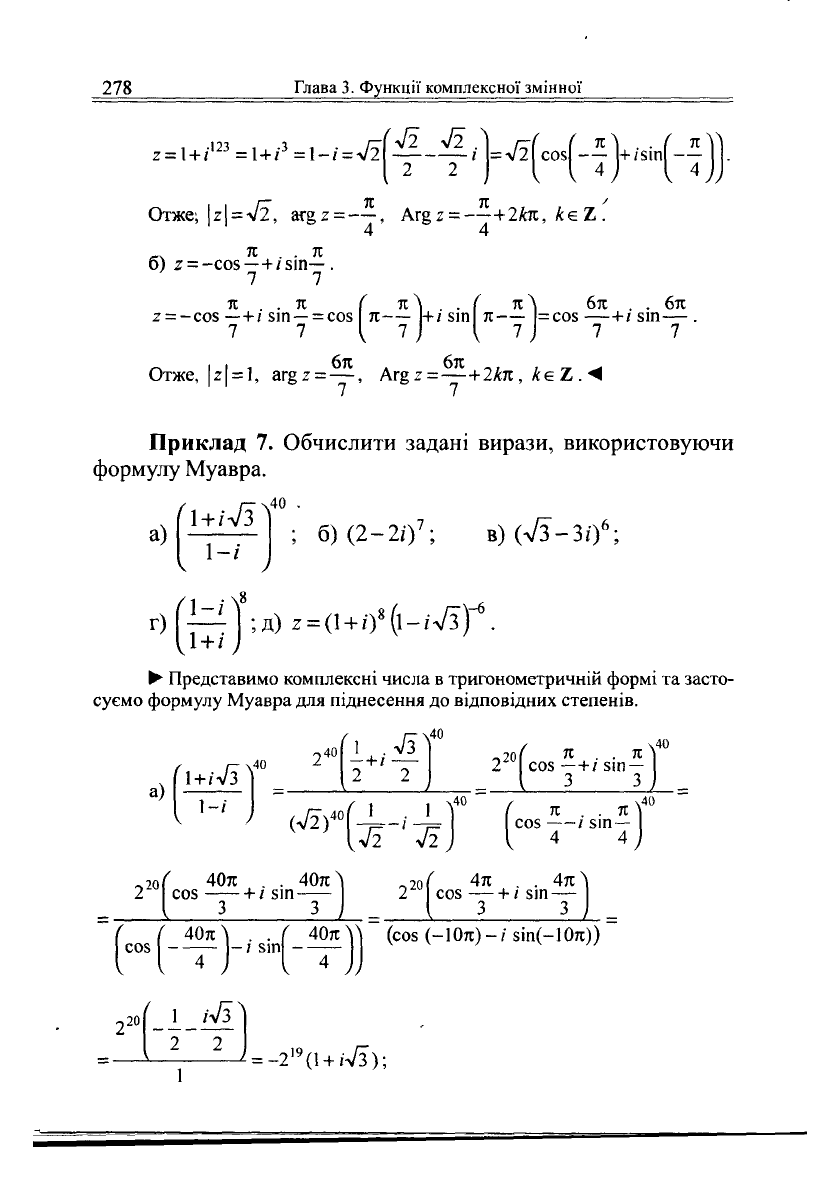
278

Глава 3. Функції комплексної змінної

= 1 + /

123

=! + /* =1

-'-^4'М~НМ-ї

Отже;

|2|

= л/2,

аг£2

= -—, Аг§г = -—+2&я, кє X .

ггч Я . . Я

б) Г = -С05 — +

/31П—

7 7

я . я

2 = -СОЗ VI ЗІП —= СОЗ

7 7

я ї . . ( п\ 6я . . 6я

Я +' 51П Я =СОЗ +

ЗІП

7 І І 7 І 7 7

Отже,

|г| =

аг§2=-^,

Аг§г=^-+2кп

, /Іє 2 .

Приклад

Обчислити задані

вирази,

використовуючи

формулу

Муавра.

а)

г)

1-/

V У

+ /

; б)

(2-2І)

;

в)(л/3-Зі)

д) г =

і)

(і-іл/з)Г

• Представимо комплексні числа в тригонометричній формі та засто-

суємо формулу Муавра для піднесення до відповідних степенів.

а)

1 +

1-/

ч40

,40

1 .л/3

—+/ —

2 2

ч40

-,201 Я . . Я

2 соз—+/ зіп —

ч40

Я . Я

соз —/ зіп —

4 4

20 ( 40л . 40я

2 соз VI зіп

т20|

4л 4я

2 соз — + / зіп —

' 40л^ . . ( 40яУ\

соз

; зіп

4 ) І 4 ^

(соз (-10л)-/ зіп(-ІОл))

-I-

_/7р

2 2

= -2

(1 +

іч/з);

§ 1.

Комплексні числа

279

б)

(2-2/)

= 2

(1-/)

= 2

\Л)

^=--±=І\

]

л/2"^СО5^|у/5іп^-^|

л/2^со

= 2

V2^со5^-2я^+/5Іп^-2л^^=2

л/2^со

7пЛ

. ( 7к

51П

. я

зіп—

л/2

2 ' 2

= 2

72^(1+/) = 2

(1+/);

в)

(л/З-3/)

=(л/з~)

-2

, зі

І созбі-— 1+ /зіп

2 2

(соз(-2тс) + /зіп(-2тс)) = З

= 1728 ;

)

,л/2 л/2 ,

г)

соз(-2л) + /зіп(-2л)

соз2я+ /зіп2л

„

|С03|-^

+/ЗІП

Я . Я \

соз—+

; зіп

—

4 ]

д)

=(і

/)Чі-/7зТ=^^=

(1-/л/3)

1-/^

2 ' 2

я . . я

СОЗ

І-/31П

—

соз2я+/зіп2я

соз

+ /зіп[

у\

4 соз(-2я)+/зіп(-2я) 4

Приклад 8. Знайти всі значення кореня заданого степеня

з комплексного числа

і)

У-І; б) >/-! +

; в) 5|л/2

ТІ

. . я

соз—н

зіп —

6 6

280

Глава 3. Функції комплексної змінної

• Зводимо комплексне число г до тригонометричної форми

2 =

/-(С05ф

/5ІПф)

і застосовуємо формулу для визначення значень кореня:

пГ пГ ( ф +

2л£7Х

. . ф + 2л£7гЛ

л/2=л/г СОЗ- + І31П- ,

к=0,п-\.

{ п п )

а) ІГЇ.

Тут г = -1. Тригонометрична форма: 2 = -1 = созл + /зіпя, бо

| =

|-1|

= 1, аг§2=аг§(-1) = л.

Отже,

маємо:

С05Л

/51ПЛ

Значення 2

заданого кореня отримуємо так:

- л + 2гсл . . к + 2кп , . , „ „

= соз + / зіп , де к =0,1, 2,3.

к = 0: 2г\ = соз —у-1 зіп — =—(1 + '),

4 4 2

к = \ :

к = 2

гі = 3:

Зтс

Зтс л/2.

соз

1-/'

зіп— = —(-! + /'),

5л . 5л л/2

СОЗ

Н/

ЗІП

= (-1-0,

7л .7л 72,

соз — + / зіп— = (1 - 0 •

4 4 2

Всі корені знаходяться на колі з центром у точці 2 = 0 і радіус якого

дорівнює одиниці, і на однаковій відстані один від одного (рис.3.5а).

а)

б)

Рис.3.5

б)

7-1+7.

Тут 2 = -1 + /.