Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. т а ін. Вища математика у прикладах та задачах. Ч 3

Подождите немного. Документ загружается.

§3.

Ряди

Фур'є

251

Підрахуємо коефіцієнти Фур'є. Оскільки одержана функція парна, то

Ь„=0.

сіх =

І 2 3 \

X X

_2_

пп

< х

2 4

' X

кпх , І

соз сіх =

2 кп:

х 1 ,| . лих

X \СІ\ ЗІП

2 2

х--

51П-

лих

. кпх , 2 г кпх

(1 -х)зіп ах = (1 -х)зіп

СІХ

пп

2 ли • 2

]0-х)с/\

СОЗ-

ЛИХ

2 ) к

4 . лих

(І -х)соз

2 2

4 е кпх ,

о л и"

соз ли -

2 2

я и

-^у(соз ли +1) = --+1) =

7ГЛ я и

•у , и-парне,

ли

0, и-непарне.

Отже,

(2и)

-\ =

•

Підставимо знайдені коефіцієнти в ряд

Дх) = -^- +

соз

лих

/1=1

Отже,

„ , 1 8^1 л-2их 18^1

/(х) = > ^-соз = -> соз лих , Ух.

З я

=і(2и)

2 3 л

„Іі(2и)

Сума ряду збігається до /(х) \/х, бо функція неперервна для \/х.

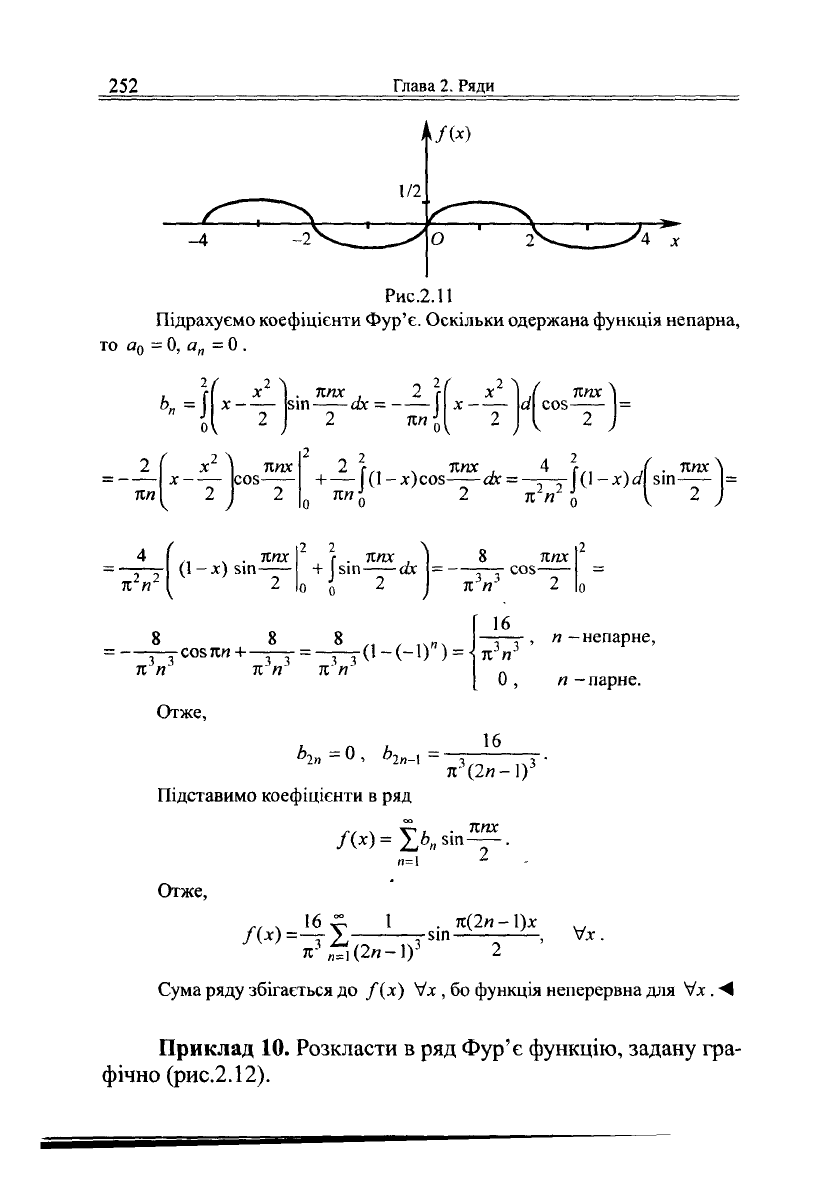
б) розкладання в ряд Фур'є по синусах.

Продовжимо функцію /(х) = х-— на відрізок

[-2,0]

непарним

чином та періодично продовжимо отриману функцію на всю числову вісь

(рис.2.11).

Маємо 1 = 2, Г = 2/ = 4.

252

Глава

Ряди

Рис.2.11

Підрахуємо коефіцієнти Фур'є. Оскільки одержана функція непарна,

то

а„ = 0 .

(•( X І . лих , 2 г| X І / то "\

о„

= х 5Ш

сіх

= х а соз =

ІІ 2 ] 2 яиД 2 Д 2 і

— Г(1

-х)со5^^-ах

= —Дг-

(її-х)щ

зіп-^^- |=

хП ппх

—

х-

соз

ЛИ

2 2

лих

- х) зіп

2 \

. ЛИХ ,

зіп

ах

ЛИХ

•7-—

СОЗ

л и

созли

+ -

= -^

(1-(-іГ) =

И ЛИ

-З

л и

п -

непарне,

-парне.

Отже,

1п

- 0 , *2«-1 -

-3—

-3-

л (2и-1)

Підставимо коефіцієнти

в ряд

/О) = ГА

5ІП

лих

п=1

Отже,

=і(2и-1)

Сума ряду збігається

до Дх) Ух, бо

функція неперервна

для Ух.Л

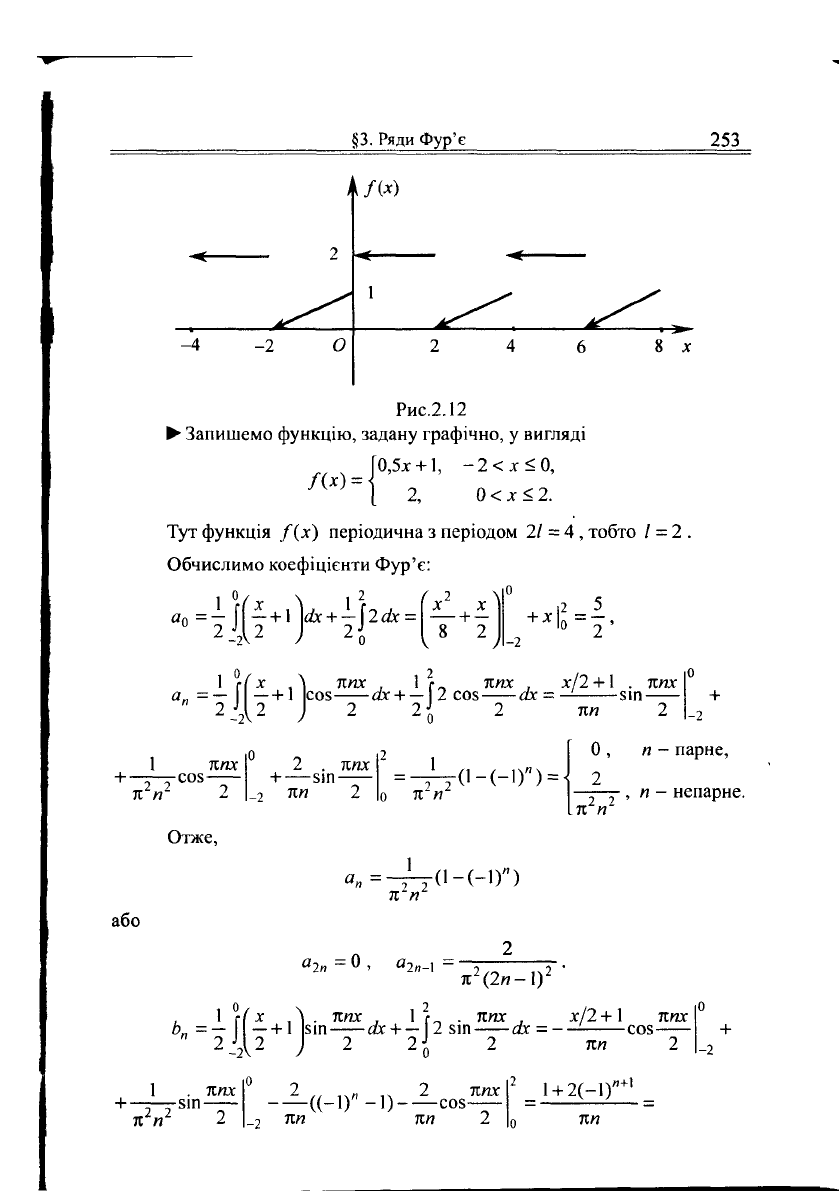
Приклад 10.

Розкласти

в ряд

Фур'є

функцію,

задану

гра-

фічно

(рис.2.12).

§3.

Ряди Фур'є

253

-2

8 х

Рис.2.12

• Запишемо функцію, задану графічно, у вигляді

\0,5х + \, -2<х<0,

0 < х < 2.

Тут функція /(х) періодична з періодом 21 = 4, тобто 1 = 2.

Обчислимо коефіцієнти Фур'є:

0/4,2

«о

і(т

г*4ї

2Л

( 2 N

х х

— +

—

8 2

V У

1 °-'

-+1

1 лих

СОЗ-

лих

, і

„ лих ,

йхл—

2 соз ах

х/2 +1 . лих

— ЗІП

ли 2

л и

2 . лих

н зіп

2 ли 2

(1-(-1)

0 Л"И

0 , и - парне,

, и - непарне.

я и

Отже,

а„ =

(і-(-і)")

або

(2п-\у

/ 1 °г(

А • лих , 1 г. . лих ,

Ь„=—

— +

зіп ох +

—

2 зіп ах

" 21^2 ) 2 2

}

ппх , х/2 +1 лих

'А- І соз

ли 2

254

Глава 2. Ряди

, п - парне,

пп

— , п — непарне.

пп

Отже,

+ 2(-1)

л+1

або

пп

А -

Л -

2тш л(2и-1)

Підставимо отримані коефіцієнти в ряд вигляду

ппх , . ппх

а„ соз +

Ь„

зіп

"22

/7=1

Отже,

/1=1

або,

після перетворень

чи+1

—

(—1)")

ппх

+ 2(-іУ" . ппх

-—^ / соз + —-—зіп —

2 пп 2

, . 5 2 1 п(2п-\)х 1 1 . 2ппх

/(*) = - + —г У -соз—

У—зіп

• /7=1 •

4 л

,м(2«-1)

2 л„ГЇ2л 2

З 1 . я(2и-1)х

я=

,2л-1

2к, к є 2 .

Сума ряду співпадає з функцією /(де) у всіх точках неперервності;

у точках розриву сума ряду така:

^(-2) = ^(2) = У(~2

У(2-0)

0±2

2 2 2

Ряд Фур'є в комплексній формі

Приклад 11. Розкласти в комплексний ряд Фур'є функцію

ГО,

- ж х < 0,

[і,

0 < х < ТІ,

періодичну з періодом 2л .

§3.

Ряди Фур'є

255

•

Задану функцію графічно зображено на рис.2.13.

А/С*)

-2я

«*

•

•*

2я

Зтс 4л х

Рис.2.13

Ця функція задовольняє достатні умови розкладання в ряд Фур'є.

Ряд Фур'є в комплексній формі:

Дх) = ІС„

""\

Знайдемо коефіцієнти Фур'є цієї функції:

= — Ах)е-

тх

ах = — \е-

тх

ах

2л

">-"

2я:

2тс

—

тх

іп

1-е "

- (соз(-лл) + /'зіп(-ля)) _

- соз ля

2лл/

соз

ля-1

_ . (-1)" -1

2 ял

Отже,

2ял

2ял/

0 , л - парне,

2ял

ял

л - непарне.

2л-1

2й

=0.

я(2л-1)

Підставляючи знайдені значення коефіцієнтів в ряд Фур'є в комплекс-

ній формі, отримуємо

/оо=--

/(2и-1)х

-л< х < 0, 0< х < я.

=-.

2л-1

У точках х = -я, х = 0, х = я сума ряду така:

5(0)

= і 5(±я) = і.^

256

Глава 2. Ряди

Приклад

12. Розкласти в комплексний ряд Фур'є функ-

цію

/(х) = е

, задану на проміжку (-я, я].

•

Розкладемо в ряд Фур'є 2тс -періодичну функцію Р(х), що збіга-

ється з заданою функцією на проміжку (-л, л]. Графік цієї функції представ-

лено на рис.2.14.

/(*) А

Рис.2.14

Ряд Фур'є в комплексній формі:

/(*)= Ісу".

Підрахуємо коефіцієнти Фур'є:

С„

=—

]/(х)е-'

ск

= —]е

е'

ах = — ]е

{]

т)х

ах =

2Л

•>

ОТ

•>

ОІГ

2л-

2л;

2л

іп

0 о

Ж1-ш)_

-к(І-.».) _(

-")(со5ИЛ-/5ІПНЛ)

(-1)"

(Є

-Є-

)

2л(1-ш) 2л(1-/«) ~ (\-іп) 2л

Оскільки функція неперервна на інтервалі (-л, л), то

_ -я оо іпх оо тх

є" =—: І (-1)"-^- = л

пл X (-І)"- .

2л „

_„ \-іп „

_ 1-ш

де

є (-л, л).

Сума одержаного ряду 5(дг) при х = -л, х = л така:

5(±я) =

, -я

••

сЬ л (за теоремою Діріхле). ^

§3,

Ряди Фур'є

257

Інтеграл Фур'с. Перетворення Фур'є

Приклад 13. Зобразити інтегралом Фур'є функцію

0 < х < 1,

/(х) = «0,5, х = 0, х = 1,

[0,

х < 0, х > 1.

• Задану функцію зобразимо графічно (рис.2.15).

0,5

-* >і

О і

Рис.2.15

Ця функція кусково-монотонна на будь-якому скінченному відрізку

[-/, /], оскільки складається з трьох неперервних частин. Вона також абсо-

лютно штегровна на всій числовій осі:

\\/(\х)\ск = \0сіх + \ах + \0 <2с = 1<°°.

— оо —оо 0 !

Отже, таку функцію в точках її неперервності можна подати через

інтеграл Фур'є:

/00 = — [сіа [/(і)со&а(і-

х)сі(.

тс і \.

Г ьіп а(і - х)

Для заданої функції маємо:

/(х) = — | ^со5а((-х)сіі сіа=— |

(о )

1 Г 5іпа(1 -х) + $'тах 2 Г 1 .а а(\-2х)

-'І

сіа = — \

51П—

С08-

тс '

а 2

сіа =

сіа.

У точках розриву х = 0 та х = 1 інтеграл Фур'є дорівнює значенню

/0Г-0) + /0Г + 0)

2 2 '

Таким чином, знайдений інтеграл Фур'є зображує дану функцію на

всій числовій осі.

258

Глава 2. Ряди

Зокрема, якщо х = 0 , то дістанемо

1 2 і- 1 . а а , 1

зіпа ,

/(0) = — = — —зіп—соз—аа = — сіа,

2 к І а 2 2 тс І а

звідки

є зіпа , тс

сіа =

І «

Таким чином, ми обчислили інтеграл, який за формулою Ньютона-

Лейбніца не обчислюється, оскільки первісна від

ЗІП

не виражається че-

рез елементарні функції. А

Приклад

14.

Зобразити інтегралом Фур'є функцію

е~

0<х<+«>,

Дх) = <-е

-°о<х<0,

х =

• Ця функція задана на всій осі і кусково-монотонна на будь-якому

скінченному відрізку [-/, /], оскільки складається з двох неперервних час-

тин і має один розрив першого роду при х = 0 (рис.2.16).

Рис.2.16

Переконаємось, що ця функція абсолютно інтегровна:

-е-*\'~=2<<

\\/(х)\сіх

\е

сіх

\е~

сіх

= е

Отже,

задану функцію можна зобразити інтегралом Фур'є. Оскільки

ця функція непарна, то інтегральна формула Фур'є має вигляд:

§/(і) зіп аі

сії

зіп осе

і/а.

§3.

Ряди Фур'є

259

Для заданої функції маємо:

Іе

'зіпос/сії

зіп ах ага.

Інтегруючи частинами, знаходимо

Звідси

|е ' зіпа/а? = а-а

|е 'зіпа/аї.

І -І • ,

\е

втаї сії

= г

+ а

(1)

Підставляючи отриманий вираз у формулу (1), отримаємо

, . 2

Г азіпах , , . .

/(*) = - г-о'а, хє (-оо, +оо).^

тс і

+ а

Приклад 15. Зобразити інтегралом Фур'є в комплексній

формі функцію

е~

, 0<х<+°°,

/(*) =-І 0, -~<х<0,

0,5,

х = 0.

• Скористаємось формулами

Обчислимо внутрішній інтеграл:

\Ді)е~

іаІ

сіі

= \е"

е-

,а1

с!і=

Іе-'

0+т)

сіІ-

(О

-Ц\+іа)

/СХ

о о

/а

)

Підсіавимо отримане значення у формулу (1). Отже, комплексна фо-

рма інтеграла Фур'є прийме вигляд:

і 7 е

ІШ

Дх)

— [

—

сіа. <

2к

+ /а

Приклад 16. Знайти косинус-перетворення Фур'є та си-

нус-перетворення Фур'є функції /(х) = е~

, х > 0.

260

Глава 2. Ряди

• Знаходимо косинус-перетворення Фур'є:

Рс (а) =./— \/ (/) соз а/

сії

(пряме).

Ї2

°°

/(х) = д[— | Рс (а) соз ах і/а (обернене).

Для заданої функції маємо:

-(а) = Д— Ге"'соз а/Л.

Інтегруючи частинами, отримуємо

С05ОІСІІ = •

Отже,

Тоді

Звідси

= (17

/ї._і_

/(х)

= е =

/- І

/-—5—-созахсЛх.

о а +1 2

Знаходимо синус-перетворення Фур'є:

тс

(а) =

/— ]/(/)зіпа/<Л

(пряме).

7"(х) =

|— ] (а) зіп ах сіа (обернене).

Для заданої функції маємо:

;

(а) =

(— ]е зіпа/й?/.

Інтегруючи частинами, отримуємо

г -і • л

Іе зіпа/а/ = —

п а

Отже,