Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. т а ін. Вища математика у прикладах та задачах. Ч 3
Подождите немного. Документ загружается.


§
1,
Комплексні числа
281
Тригонометрична форма числа: 2 = -1 + і =
|2|
= |-1 + /| = 72, аг§
2=аг§
(-1+/) = ^*-.
Зл . Зл ^ ,
соз
1-
;зіп— , бо
4 4 І
Отже,
маємо:V-1 +
/'
= VI
^|
Значення г
к
заданого кореня отримуємо так:
Зл . . Зл
соз — + і зіп—
4 4
=
71
Зл Зл ^
— + 2кп
—
+
2кп
4 -4
соз —
+ і
зіп
—
,де
4=0,1.
4=0:
2
П
= ТІ [ соз — + /' зіп— |,
0
(8 8 і
4 = 1:
=
72
соз
•
+ І 5ІП-
1ІЛ
8 8
Корені розташовуються на колі з центром в точці г = 0 і радіус якого
72 (рис.3.56).
в)
5/72
І
соз
—
+ / зіп — ].
V І б 6)
Число 2 = ТІ! соз — + / зіп —
І
6 6
,
тому за формулою для обчислення коренів маємо:
задане в тригонометричній формі,
-к
4 = 0:
4 =
1
:
'72
—
+2кп
соз
-
+ / зіп
—
- +
2кп
де 4=0,1,2,3,4
= '^(соз^+/зіп^
^
зо зо
13л
=
'72
соз
30
-
+ / 51П-
Зл
зо

282
Глава
3.
Функції комплексної змінної
юЛГІ 4У7С
.
4Утс
к
= 4 : 2
4
= ->/2 соз г-1 зіп
4
1 ЗО ЗО
Приклад
9.
Знайти корені заданих рівнянь
і
зобразити
їх
на комплексній площині.
а)2
4
+1
= 0;
б)2
2
+1-/
= 0.
•
а) г
4
+1 = 0 .
Запишемо задане рівняння
у
вигляді
ТОДІ
2 ,
тобто розв'язання задачі зводиться
до
знаходження всіх
значень кореня четвертого степеня
з
комплексного числа,
що
дорівнює
-1.
Знаходження всіх значень вказаного кореня,
а
також
їх
зображення
на
комплексній площині наведено
в
прикладі
8 п.а).
б)
2
2
+1-/
= 0.
Запишемо задане рівняння
у
вигляді
Тоді
2 = V-
І
+ / ,
тобто розв'язання задачі зводиться
до
знаходження
всіх значень кореня другого степеня
з
комплексного числа,
що
дорівнює
—
І
+ /.
Знаходження всіх значень вказаного кореня,
а
також
їх
зображення
на
комплексній площині наведено
в
прикладі
8 п.б). А
Приклад 10. Довести рівності.
а
) к-
Г
2І=кН
Г
2І;
б)
,
к|*0;
в)
аг§(2,
•
г
2
) =
аг§2!
+
аг§г
2
;
г) (г,
•
г
2
) = г,
•
г
2
.
•
Представимо комплексні числа
г, та г
2
в
показниковій формі:
<-\
~
Г
\
е
'
А
2 ~ '2
де|2,|
= /-,,
\г
2
\
= г
2
,
аг§2,=ф,, аг§2
2
=ф
2
Тоді
_
. - -
Гґ
-,'(Фі+ф
2
)
2,
-2
2
-
Г
Х
Г
2
Є
,
2
2
Г
2
Отже,
Фі
,'Ф2
£і_
_ И.
е
'(<Рі-фг)

§
1.
Комплексні числа
283
Доведемо задані рівності,
а)
1-і -г
2
| = |г,| \г
2
\.
б)
ІІІІ
к
2
|"
в) аг§(г,
•г
2
) =
аг&2
]
+
аг§2
2
.
аг§(
2
,
-2
2
)
=
ф,
+ф
2
=аг§2, +аг§2
2
.
г,
•
2
2
.
Г)
(2, -2
2
)
=
2,
•І
2
.^
Приклад
11.
Навести геометричний опис множини всіх
точок
комплексної площини,
що
задовольняють нерівності.
ГІІГП2І<1,
а)
Кег>0;
б)\Ке2
<1; -
ч
"
1
в)
0<Ке2<1:
т)\і-і\>\;
д)1<|2-і|<3;
е)
|
тс
-
аг§
г
|
<
71
•
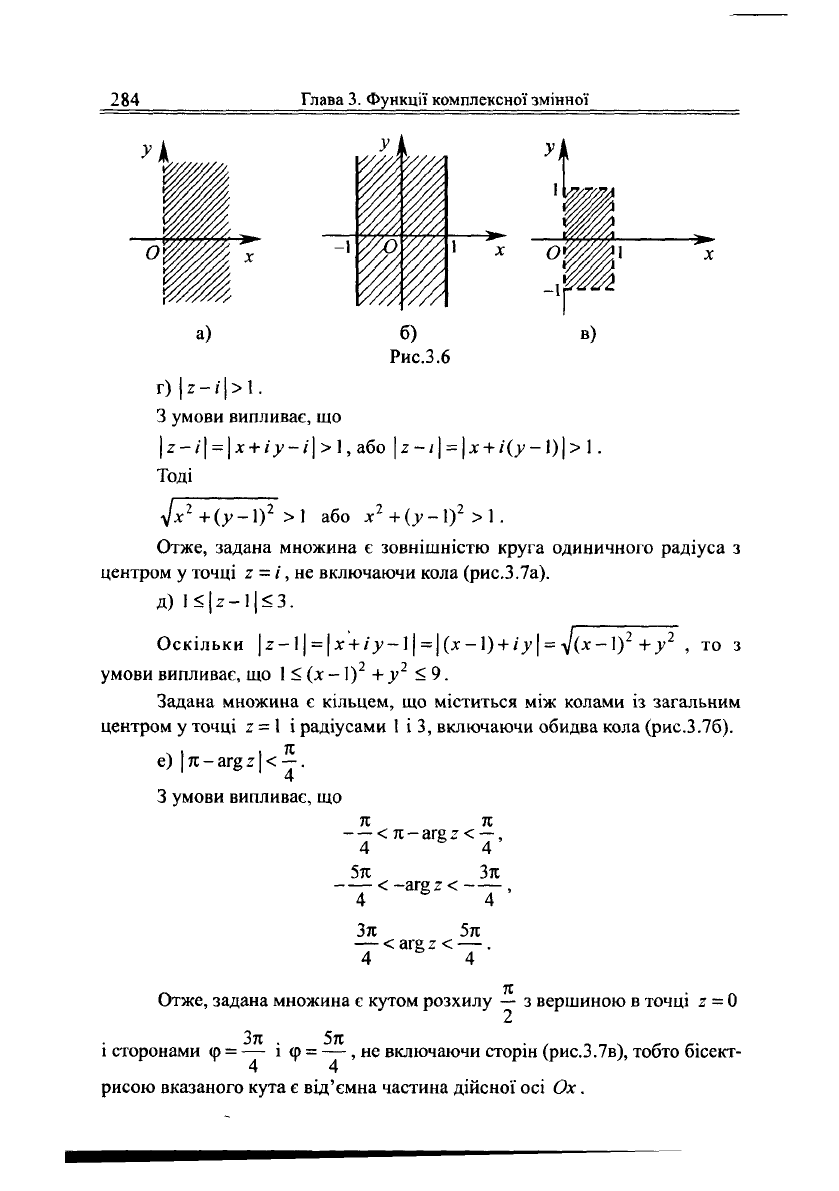
а)
Ке2>0
.
Кег
= Ке(х
+
іу) = х, х>0.
Задана множина
є
півплощиною,
що
розташована праворуч уявної
осі,
причому точки
осі не
належать
їй
(рис.3.6а).
б)
|ЯЄ2|<1
.
|Яе2| = |Яе(х + /»|<1 =>
|л:|<1,
тобто
-1<х<1.
Задана множина
є
смугою,
що
розташована
між
прямими
х =
-1,
х
= 1,
включаючи
ці
прямі (рис.3.66).
Г|ІТ
2
|<1,
|0<КЄ2<1.
\\у\<1,
\-1<у<1,
З умови випливає,
що •{
тобто
<
[0<х<\,
[
0<х<1.
Задана множина
є
прямокутником,
що є
перетином смуг, розташова-
них
між
прямими
у = -\, у = \ та х = 0, х = 1, не
включаючи самі
ці
прямі.
Отже, маємо прямокутник
з
вершинами
-/, 1-/', / (не
включаючи
сторін) (рис.З.бв).
284
Глава 3. Функції комплексної змінної
а)
Г)
|2-||>1.
З умови випливає, що
\г-і\ = |х + іу-і\ > 1, або \ г-і\ = \х + і(у-1)| > 1.
Тоді
4х
г
+(у-\)
2
>1 або д:
2
+(у-1)
2
>1 .
Отже, задана множина є зовнішністю круга одиничного радіуса з
центром у точці г = і, не включаючи кола (рис.3.7а).
д)
1<|
г
-і|<3.
то з
Оскільки
\2-]\
=
\х'+іу-]\=\(х-\) +
іу\ =
лІ(х-])
2
+ у
2
,
умови випливає, що 1 < (х -1)
2
+ у
2
< 9.
Задана множина є кільцем, що міститься між колами із загальним
центром у точці 2 =
1
і радіусами 1 і 3, включаючи обидва кола (рис.3.76).
е) |тс-аг§2|<^.
З умови випливає, що
ТІ тс
- — <тс-аг§2<-,
4 4
5тс Зтс
-—
<-аг§2<-—,
4 4
Зтс 5л
— < ага 2 < —.
4 4
Отже, задана множина є кутом розхилу з вершиною в точці 2 = 0
і сторонами ф = — і ф = —, не включаючи сторін (рис.3.7в), тобто бісект-
4 4
рисою вказаного кута є від'ємна частина дійсної осі Ох.
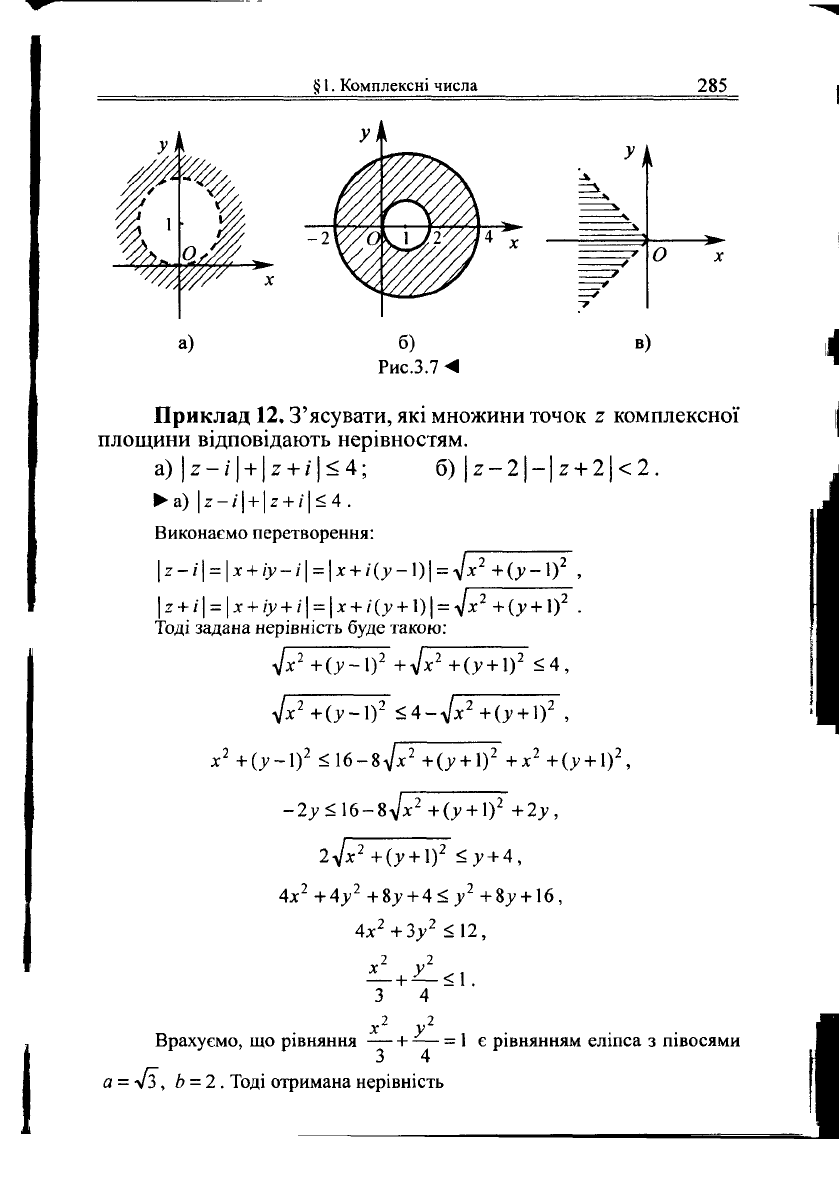
§
1.
Комплексні числа
285
0 б) в)
Рис.3.7^
Приклад 12. З'ясувати, які множини точок 2 комплексної
площини відповідають нерівностям.
а) |г-/| + |г + /|<4;
б)|2-2|-|г
+ 2|<2.
• а)
|
г - і
|
+12
+ /1
< 4 .
Виконаємо перетворення:
\2-і\
= \х + іу-і\ = \х +
і(у-1)\
= 4х
2
+0>-1)
2
,
I
2 + І
|
=
|
X + Іу + І
І
=
І
X + І(у + 1)
І
= -у/*
2
+(У+1)
2
•
Тоді задана нерівність буде такою:
УІХ
2
+0>-1)
2
+УІХ
2
+(у + \)
2
<4,
УІх
2
+(у-\)
2
<4-уІх
2
+<у + \)
2
,
х
2
+(у-\)
2
<16-8д/х
2
+(у + \)
2
+х
2
+(у + 1)
2
,
-2у<\6-8лІх
2
+ 0> + 1)
2
+2у,
2уІх
2
+ (у + \)
2
< у + 4,
4х
2
+4у
2
+&у + 4<у
2
+8у + 16,
4х
2
+3>>
2
<12,
2
2
З 4
х
2
У
2
Врахуємо, що рівняння -у + —^- =
1
є рівнянням еліпса з півосями
а = -Уз, Ь = 2 . Тоді отримана нерівність
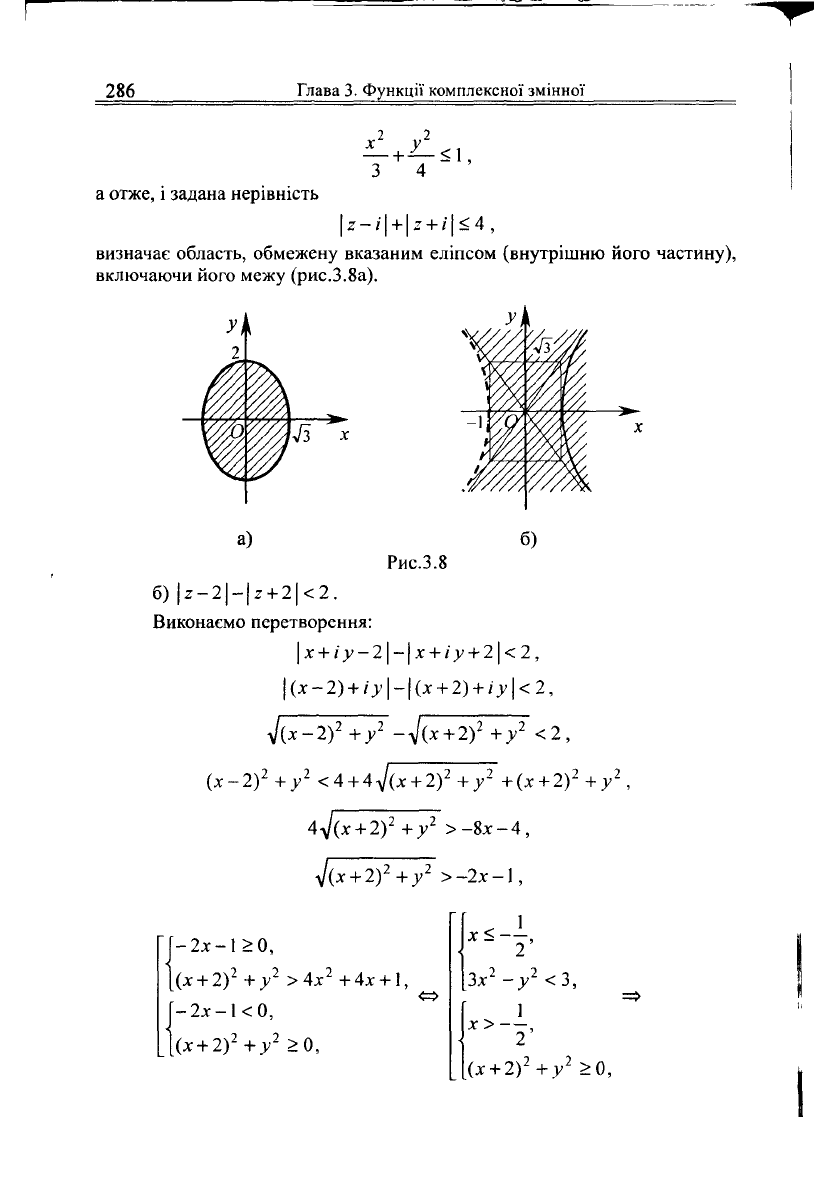
286
Глава
3.
Функції комплексної змінної
2
2
З
4
а отже,
і
задана нерівність
|
2 - /
|
+
|
2 + /
|
< 4 ,
визначає область, обмежену вказаним еліпсом (внутрішню його частину),
включаючи його межу (рис.3.8а).
а)
б)
Рис.3.8
б) \г-2\-\г
+ 2\<2.
Виконаємо перетворення:
|х
+
/>'-2|-|х
+ /у + 2|<2,
І
(х - 2) +
/>-1
-1 (х + 2) +
/
у
І
< 2,
4(х-2)
2
+у
2
-д/(х+2)
2
+/
<2,
(х-2)
2
+ у
2
<4+4
А
/(х
+ 2)
2
+У
2
+(х + 2)
2
+ у
2
,
4уІ(х
+ 2)
2
+у
2
>-8х-4,
4(х + 2)
2
+у
2
>-2х-\,
[-2х-1 >0,
1(х + 2)
2
+ у
2
>4х
2
+4х + 1,
Г-2л:-1
< 0,
\(х
+
2)
2
+у
2
>0,
X
<
2'
Зх
2
-у
2
<3,
(х
+
2)
2
+у
2
>0,

§ 1. Комплексні числа
287
х
2
-^<\,
З
х> --
1
_(х + 2)
2
+у
2
>0,
х<
х
2
-^<и
х,уе
К.
Отже, задана нерівність визначає частину площини, що розташована пра-
2 У
2
воруч лівоївітки гіперболи х —— = 1, не включаючи цю вітку (рис.3.8б). Л
Приклад 13. Знайти множини точок на площині комплекс-
ної змінної г, які задовольняють задані умови.
а) 0 < аг§ < —
І + 2 2
В)
КЄ2
4
> ІГП2
4
.
• а) 0<аг§-—-< —.
І+2
2
б) -<ащ(г +
і)<-;
Виконаємо перетворення, поклавши 2
/ - 2
І+2
, ДЄ 2 = Х + І у .
2=
1
-
2
= і-(х + іу) _ ~х + і(1-у) ^ (-х +
і(\-у))(х-і(\
+ у))
І+2 І + (Х + Іу) Х + І(\ + у)
х
2
+(\+у)
2
-х
2
+1-у
2
+ і(х + ху + х-ху) _ -х
2
- у
2
+1 + 2*/'
_ _
х
2
+(\ + уУ
Отже
2 =
х
2
+(\ + у)
2
_ -х
2
- у
2
+1 + 2хі
-х
2
-у
2
+\
+
1-
2х
х
2
+{\ + у)
2
л:
2
+(1+>')
2
х
2
+(1+у)
2
-
Вважаючи, що 2 = X + ії , маємо
Х =
_-Х
2
-у
2
+ :
х
2
+(]
+ у)
2
У =
2х
х
2
+(\ + у)
2
'
тс
Оскільки за умовою 0 < аг§ 2 < —, отримуємо
і-2 У 2х
ащ 2 = аг§ = агсі§ — = агсІ§ —
І + 2 X -
х
2
-у
2
+\

288
Глава 3. Функції комплексної змінної
В силу тієї ж умови 0 < аге 2 < — маємо, що X = —^ ^
+
} > 0.
2
х
2+ґ\ + у)2
Звідки - X
і
- у
2
+1 > 0, тобто х
1
+ у
2
< 1.
Далі з нерівності
2х тс
0<агсі§
5
—-<-
-х -у +1 2
маємо
0< : ; <+°°.
-х
2
-у
2
+1
Враховуючи, що х
2
+ у
2
< 1, з останньої нерівності отримуємо, що
х > 0 , тобто задана множина визначається системою нерівностей
[х>0,
х
2
+у
2
<1.
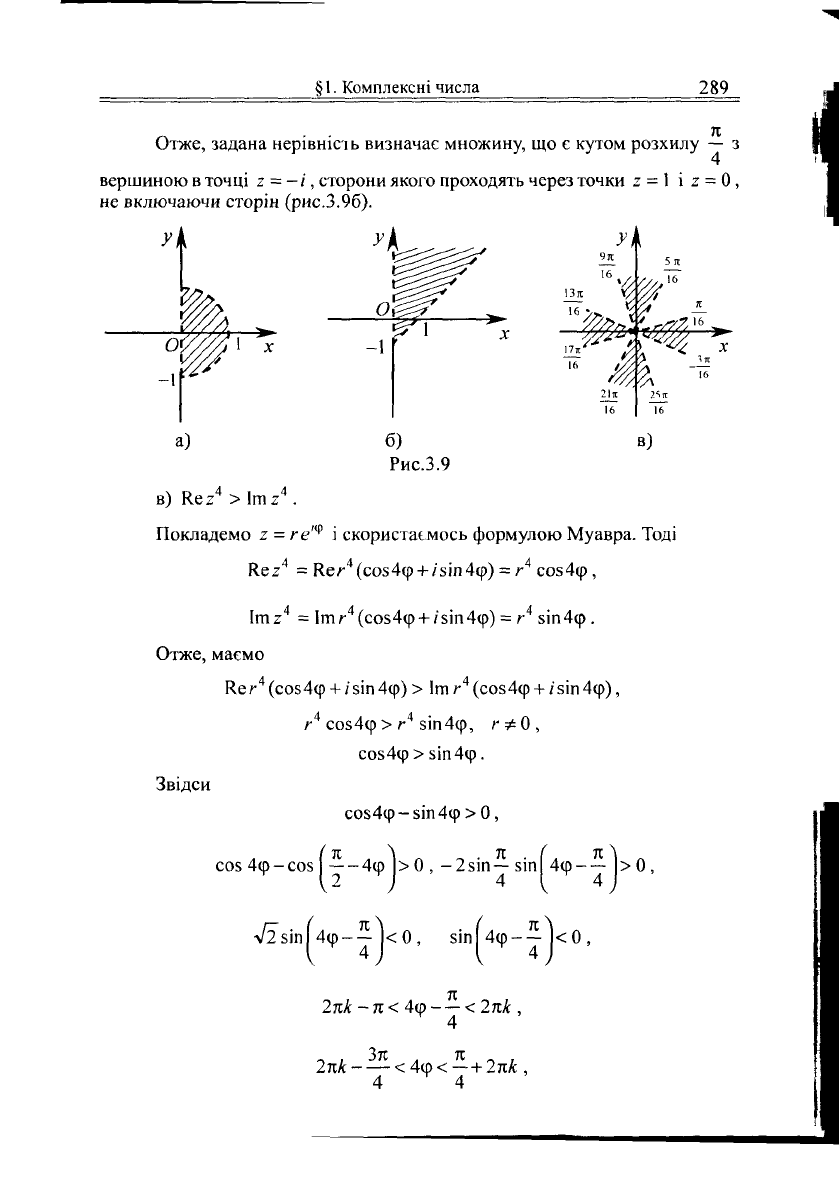
Отже, задана нерівність визначає множину точок, що є правою поло-
виною круга радіуса
1
з центром у точці г = 0, не включаючи межу (рис.3.9а).
б) — < аг§ (г + /) < —.
4 2
Виконаємо перетворення, поклавши 2 = 2 + і, де 2 = х + / у:
2 = г + і = х + іу + і = х + і(у + ї).
Тоді
К
ащ(г + і) = аг&2 = ащ(Х+ і¥) = агсЩ —, деХ = х, К=>> + 1.
-А
тс
тс
Оскільки за умовою — < аг§ 2 < — , маємо, що X = х > 0.
Далі з нерівності
маємо
л
у
+
1
л
—
<агсі£- < —
4
6
х 2
]<-
<+°о,
*±1>і,
£±!-і>о,
у
"
х+1
>о.
XX
X
Враховуючи, що х > 0, отримуємо
у-х +
1>0,
Гу>х-1,
х>0, |х>0.
§1.
Комплексні числа
289
Отже, задана нерівність визначає множину,
що є
кутом розхилу
— з
4
вершиною в точці 2
=
- /, сторони якого проходять через ТОЧКИ 2
=
1
І
2
= 0 ,
не включаючи сторін (рис.3.96).
9к_
16
5д
2ІЯ
2^к
16
16
в)
а)
В)
КЄ2
4
>
ІП12
4
.
Покладемо
2 = ге"
9
і
скористаємось формулою Муавра. Тоді
Кег
4
=
Ке/-
4
(соз4ф
+ /5Іп4ф) = г
4
соз4ф,
ІГП2
4
=
ІтИ(соз4ф
+ /зіп4ф)
= г
4
зіп4ф
.
Отже, маємо
Кег
4
(соз4ф
+
/зіп4ф)
>
Ітг
4
(соз4ф
+
/зіп4ф),
г
4
соз4ф
> г
А
зіп4ф,
г^О,
Звідси
соз4ф
>
зіп4ф.
соз4ф-зіп4ф
> 0,
соз 4ф-соз
|у-4ф |> 0 ,
-2зіпу
зіп|4ф-^
|> 0,
"У2зіп^4ф--^<
0,
зіп^4ф--^<0,
2лк
-
п<
4ф <
2пк
,
4
2пк- —
<4ф<— +
2пк ,
4
4

290
Глава 3. Функції комплексної змінної
л4 Зл л пк
— <ф<— + —, 4 = 0,1,2,3.
4 = 0:
4 = 2
Зл л
— <Ф< —,
16 16
13л 17л
< ф<
16 16
4 =
1
:
4 = 3:
5л 9л
— <
Ф
< —,
16
т
16
21л 25л
<
Ф
<
16 16
л
Отже, задана нерівність визначає чотири кути розхилу —> з верши-
4
л
ною в точці 2 = 0, бісектрисами яких є промені ф =
1-
л4, 4 = 0,1,2,3,
16
не включаючи сторін кутів (рис.3.9в). Ч
Приклад 14. З'ясувати, які лінії комплексної площини за-
дані вказаними умовами.
а) Ке
—
= —, а > 0 ;
2 а
б) Іт^—- = 0.
2 +
1
• а) Яе- = -, а>0 .
2 а
Перетворимо ліву частину рівності:
х
—
іу
Яе-
= Яе
2 Х + Іу
= Яе-
(х + іу)(х-іу)
= Яе
х-і
у
2 2
X + у
= Яе
х
2
+ у
1
Отже, маємо —— = — , де х
2
+ у
2
Ф0, тобто рівність має місце в
х +у а
усій комплексній площині, крім точки 2=0. Далі, продовжуючи перетво-
рення, отримаємо ах = х
2
+ у
2
, або х
2
—
ах + у
2
= 0 , або
а
х
2
* 2 а
2
,
+у =
т-
Отже, одержали коло з центром у точці С
тою точкою 2 = 0 (рис.З.ІОа).
а „| а
—, 0 радіуса — з виколо-
^
2 ) 2
