Коган В.Е., Зенин В.С., Пенкина Н.В. Физическая химия. Часть 2. Химическая кинетика

Подождите немного. Документ загружается.

В. Е. Коган, Г. С. Зенин, Н. В. Пенкина

130

При трехмерном движении вероятность того, что молекула будет иметь

скорость в пределах и , и , и

xdxyydyzzdz+++

  

 

, выражается произведени-

ем трех одинаковых вероятностей вида (2.240)

3/2

mC T

dN m

e dxdydz

−

⎛⎞

⎜⎟

⎝⎠





, (2.243)

где

С – полная скорость молекулы в объеме

(

)

2222

Cxyz=++





. Не приводя

вывода отметим, что доля молекул, скорости которых лежат в пределах от

С до

C + dC независимо от направления, определяется уравнением Максвелла для

распределения молекул по скоростям

3/2

mC T

dN m

eCdC

−

⎛⎞

=π

⎜⎟

⎝⎠

. (2.244)

Кривые зависимости от

С доли молекул, скорости которых лежат в пределах от

С до С + 1, при двух температурах приведены на рис. 2.28.

Кривые проходят через максимум,

смещающийся при повышении темпера-

туры в сторону бóльших скоростей. Это

означает, что с повышением темпера-

туры увеличивается число молекул,

движущихся с повышенными скоростями. Действительно, как наглядно видно

из рис. 2.28, площадь, лежащая под кривой и ограниченная слева ординатой

(например, ординатой, отвечающей

510 м/сC =⋅ ), равная доле молекул, ско-

рость которых превышает значение

510 м/сC =⋅ (заштрихованная область),

больше для кривой 2 ( 373 K

T = ),чем для кривой 1 ( 273 KT

). Максимуму со-

ответствует

наиболее вероятная скорость

, которую найдем, дифференци-

руя

1 dN

NdC

по С и приравнивая производную нулю:

Рис. 2.28. Кривые распределения молекул

кислорода по скоростям для двух темпе-

ратур: 1 –

T = 273 K, 2 – T = 373 K

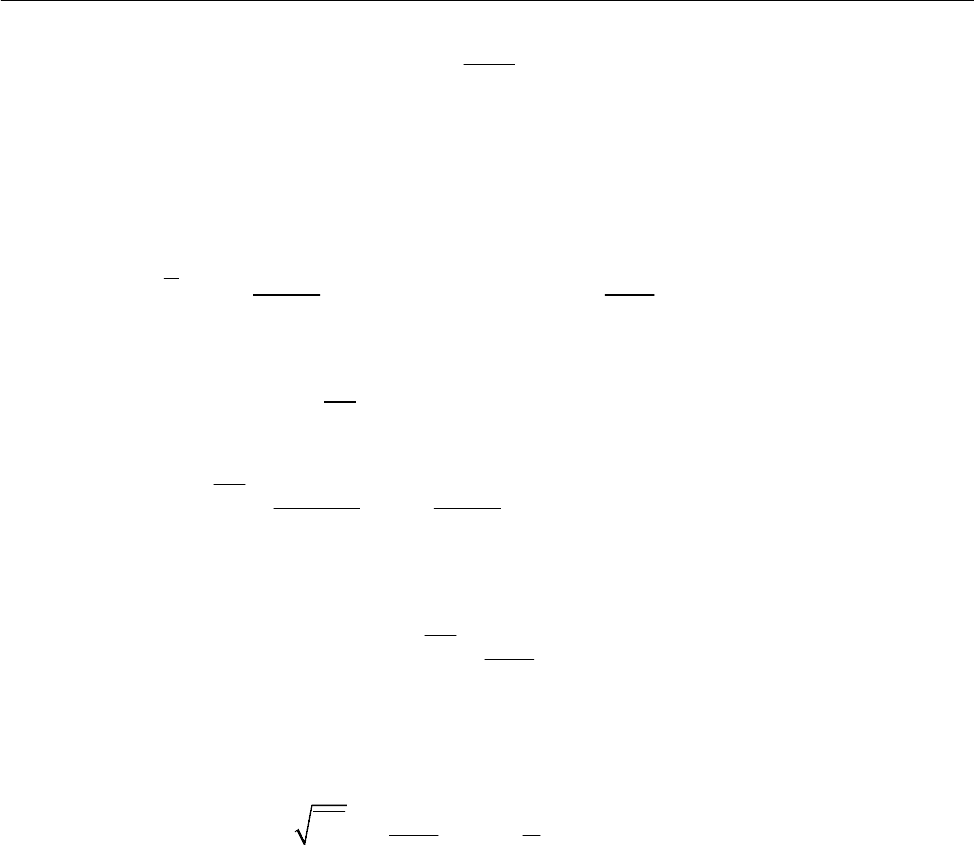
Х и м и ч е с к а я к и н е т и к а

131

1/2

2 T

⎛⎞

α=

⎜⎟

⎝⎠

. (2.245)

Для нахождения

средней скорости движения молекул при данной тем-

пературе умножим обе части уравнения (2.244) на

С и проинтегрируем полу-

ченное выражение от нуля до бесконечности:

3/2 1/2

4 1,128

mC T

CeCdC

∞

−

⎛⎞ ⎛⎞

=π = = α

⎜⎟ ⎜⎟

ππ

⎝⎠ ⎝⎠

∫

. (2.246)

Для определения

средней квадратичной скорости сначала вычислим

средний квадрат скорости

C :

3/2

mC T

CdN

CeCdC

∞

−

⎛⎞

==π

⎜⎟

⎝⎠

∫

. (2.247)

Интегрируя выражение (2.247), получим

3 T

, (2.248)

извлекая квадратный корень из которого, найдем среднюю квадратичную ско-

рость:

1/2 1/ 2

1, 224

⎛⎞⎛⎞

== = α=

⎜⎟⎜⎟

⎝⎠⎝⎠

. (2.249)

Таким образом, найденные средние скорости различаются по величине и рас-

полагаются в следующей последовательности:

uC>>α.

Кратко рассмотрев основные вопросы, связанные с распределением мо-

лекул по энергиям и скоростям, остановимся на некоторых моментах, касаю-

щихся межмолекулярных столкновений. В первую очередь условимся, что же

именно будем называть столкновением. Дело в том, что, строго говоря, молеку-

лы не имеют определенных размеров, так как плотность электронных облаков

нигде не

становится равной нулю. Однако такое представление не позволяет

даже определить само понятие соударения. Поэтому обычно используют гру-

бую модель, уподобляя молекулы жестким сферам различных диаметров. Рас-

смотрим в рамках такой модели смесь газов, состоящих из молекул типа А

типа В,

массы которых

иmm, а диаметры –

D соответственно. Столк-

новение (соударение) определим как событие, когда осуществляется контакт

В. Е. Коган, Г. С. Зенин, Н. В. Пенкина

132

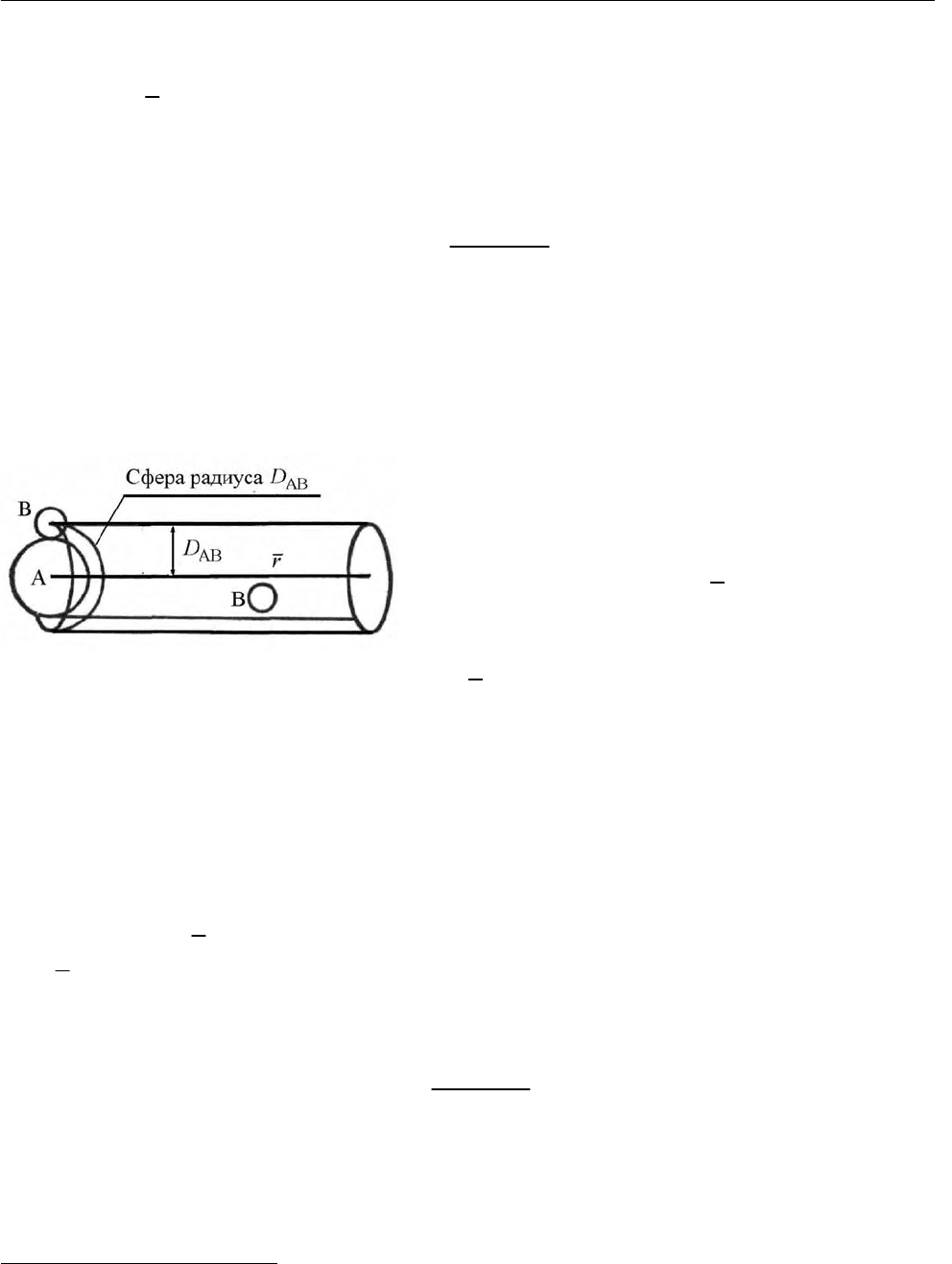
Рис. 2.29. К расчету числа двойных соударе-

ний

двух воображаемых сфер. Для расчета числа соударений молекулы А

предста-

вим ее движущейся в произвольном направлении со

средней относительной

скоростью

r в то время, как молекулы В будем считать неподвижными. Со-

ударение произойдет в том случае, если центр молекулы В

расположен на рас-

стоянии, не превышающем

от линии движения молекулы А

(рис. 2.29). Общее число соударений в секунду

молекулы А

с молекулами В равно произведению объема, описываемого за се-

кунду сферой радиуса

, на

– число молекул В в единице объема, т. е.

частичная концентрация

Объем равен

rπ , а число столк-

новений –

AB B

ν . (2.250)

Входящая в это выражение площадь

π называется сечением столкновения,

а величина

– средним газокинетическим диаметром столкновений или

средним эффективным диаметром столкновений. Для молекул одного вида

используют

эффективный или газокинетический диаметр D, учитывающий

взаимодействие между сталкивающимися молекулами.

Значение

r определяется выражением, похожим на выражение (2.246)

для

C , но масса m одной молекулы заменяется в этом случае приведенной мас-

сой

двух молекул:

µ=

. (2.251)

Таким образом,

средняя относительная скорость движения молекул А и В

В СИ единица измерения частичной концентрации i-й молекулы

, выраженной

числом молекул в единице объема, – один

−

(

молекула/м ).

Х и м и ч е с к а я к и н е т и к а

133

1/2

8 T

⎛⎞

⎜⎟

πµ

⎝⎠

. (2.252)

Понятно, что в случае одинаковых молекул

mmm

= и /2mµ= , а следова-

тельно,

1/2

2rC

Подставляя выражение (2.252) в (2.250) получим окончательное выражение для

числа столкновений молекулы А

с молекулами В за 1 с, т.е. частоту столкно-

вений

1/2

AB AB B

811

DDRT

⎡⎤

⎛⎞

⎡⎤

ν= π + ν

⎢⎥

⎜⎟

⎢⎥

⎣⎦

⎝⎠

⎣⎦

. (2.253)

В правой части данного равенства вместо масс молекул в кг, входящих в выра-

жение (2.251) для

, введены молярные массы М в кг/моль, а постоянная

Больцмана

k заменена универсальной газовой постоянной R.

Особо следует остановиться на вопросе используемых единиц изме-

рения.

Исходя из того, что средняя относительная скорость движения молекул

r (выражения в квадратных скобках в уравнении (2.253) соответствуют r

)

включает или

k , которые выражаются соответственно в

Дж кг м

сК

⋅

Дж кг м

моль К

моль с К

⋅

⋅⋅

, величина r измеряется в м/с. Поэтому здесь и в других

формулах, включающих среднюю относительную скорость движения мо-

лекул, все величины должны быть выражены в

системе СИ

Из соотношения (2.253) следует, что при стандартных условиях

и темпе-

ратуре 298 K молекула газа испытывает около

10 столкновений в секунду.

Выражение (2.253) позволяет также определить

среднее время между столк-

новениями

τ как обратную величину числа столкновений одной молекулы в

секунду:

Все газообразные участники реакции находятся в стандартном состоянии, т. е. их парци-

альные давления равны 1 атм.

В. Е. Коган, Г. С. Зенин, Н. В. Пенкина

134

1/2

AB B

⎡

⎤

τ=

⎢

⎥

⎣

⎦

, (2.254)

составляющее при стандартных условиях и температуре 298 K порядка

−

с,

среднюю длину свободного пробега

, т. е. пути, проходимого молекулой А

между двумя столкновениями. Вычисляется

путем умножения средней ско-

рости

C , определяемой выражением (2.246), на среднее время между столкно-

вениями

τ , определяемое выражением(2.254), а следовательно,

()

1/2

λ=

νπ

. (2.255)

Путем умножения числа столкновений одной молекулы А

[выражение

(2.253)] на частичную концентрацию этих молекул

можно найти число

двойных столкновений

молекул А с молекулами В в единице объема

м ) в единицу времени (1 с):

1/2

AB AB A B

ZD RT

⎡⎤

⎛⎞

=π + νν

⎢⎥

⎜⎟

⎝⎠

⎣⎦

. (2.256)

Полное число двойных столкновений одинаковых молекул Z можно опреде-

лить, приняв в формуле (2.264)

и введя множитель 1/2, без кото-

рого каждое соударение считалось бы дважды. Таким образом:

1/2

⎡⎤

⎢⎥

⎣⎦

, (2.257)

где

D – газокинетический диаметр (см. выше), а

– частичная концентрация

молекул.

Рассмотрение числа двойных столкновений ограничим случаем, когда

энергия сталкивающихся молекул сосредоточена лишь в двух степенях свободы

или, точнее говоря, выражена двумя квадратичными членами. Такой подход

достаточен для решения многих задач химической кинетики. Так, например,

при столкновении двух молекул достаточно учитывать лишь относительную

кинетическую энергию движения вдоль линии,

соединяющей их центры. Ска-

занное, во-первых, означает, что отсчет скоростей молекул ведется относитель-

но неподвижного центра массы (относительные скорости), а во-вторых, что бе-

Х и м и ч е с к а я к и н е т и к а

135

рутся не полные относительные скорости, а только их составляющие вдоль ли-

нии центров, которые и определяют скорость сближения молекул. Обозначив

эти составляющие через

′′

vv, запишем относительную кинетическую

энергию вдоль линии центров

в следующем виде:

() ()

AA BB

′

. (2.258)

Вычислим число столкновений, происходящих при

R, равном или превышаю-

щем некоторое критическое значение

Е, т. е. при условии

≥R .

Две сталкивающиеся молекулы рассмотрим как единую систему, обла-

дающую всего двумя степенями свободы

– по одной на каждую молекулу, что

допустимо, так как во внимание принимается только движение вдоль линии

центров. Следовательно, можно ограничиться рассмотрением двумерного дви-

жения и найти

число частиц, т. е. число пар сталкивающихся молекул, ко-

торые обладают в двух степенях свободы энергией, не меньшей

Е. При двух

степенях свободы будем рассматривать движение вдоль координат

x и y. Ана-

логично рассмотренному ранее более сложному случаю движения в трехмер-

ном пространстве [см. выражение (2.243)] соответствующий закон распределе-

ния запишется как произведение двух выражений, подобных (2.240), т. е.

mC T

dN dN dN m

edxdy

NN N T

−

⎛⎞⎛⎞

⎜⎟⎜⎟

⎝⎠⎝⎠



, (2.259)

где

С – полная двумерная скорость

(

)

222

Cxy=+



Не приводя вывода отметим, что закон распределения, выражающий до-

лю частиц, двумерная скорость которых независимо от направления лежит в

пределах от

С до C + dC определяется уравнением

mC T

dN m

eCdC

−

. (2.260)

Перейдем от скорости к энергии поступательного движения

ε :

Для нее будем использовать обозначение R, в отличие от обозначения R, использующегося

для универсальной газовой постоянной.

В более общем случае, как уже упоминалось, говорят о выражении энергии двумя квадра-

тичными членами, примером чего является соотношение (2.258).

Математически такой способ рассмотрения вполне эквивалентен движению двух частиц

вдоль одной координаты.

В. Е. Коган, Г. С. Зенин, Н. В. Пенкина

136

/2 иmC d mCdCε= ε=

. (2.261)

Подставляя (2.261) в (2.260), найдем долю частиц

−ε

, (2.262)

энергия которых лежит в пределах от до

ε+ ε. Интегрируя (2.262) по ε от ε

до бесконечности, найдем долю молекул, энергия которых равна или больше ε:

/ T

−ε

. (2.263)

Отсюда

/ T

NNe

−

(2.264)

или

ERT

NNe

−

= . (2.265)

Выражение (2.263) является единственным случаем в кинетической тео-

рии газов, когда доля молекул просто равна больцмановскому множителю

/ T

−ε k

и, что более важно, будучи полученным для двух степеней свободы по-

ступательного движения, сохраняет свое значение для любого случая, когда

энергия выражается двумя квадратичными членами. Поэтому соотношение

(2.265) может также выражать число двухатомных молекул

N с энергией ко-

лебания, равной или большей

Е.

Ранее нами было определено общее число двойных столкновений

или

Z [соотношения (2.256) и (2.257)], среди которых

N , исходя из вы-

шеизложенного, можно рассматривать как число соударяющихся пар молекул,

относительная кинетическая энергия которых вдоль линии центров равна или

больше

Е. Используя (2.265) для этого случая, мы умножаем

или

Z на

/ERT

−

, получая

ERT

ZZe

−

= , (2.266)

Х и м и ч е с к а я к и н е т и к а

137

которое выражает число двойных столкновений молекул, происходящих с

энергией, равной или большей

Е, при том условии, что энергия выражается

двумя квадратичными членами

2.2.2.2. Анализ зависимости влияния температуры на

скорость реакции с позиции кинетической теории газов

Расчет влияния температуры на скорость реакции по правилу Вант–

Гоффа, проведенный по уравнению (2.202), показывает очень резкое возраста-

ние скорости реакции при повышении температуры. Так, даже при низких зна-

чениях температурного коэффициента скорости реакции

(

)

2γ= , повышение

температуры от 273 K до 373 K приводит к повышению скорости реакции в

10≈ раз.

Объяснить столь резкое увеличение скорости реакции при повышении

температуры одним только увеличением числа соударений между частицами

исходных веществ за счет установленного кинетической теорией газов увели-

чения числа молекул, движущихся с повышенными скоростями (см. рис. 2.28),

нельзя. Действительно, в газе при стандартных условиях скорость, с которой

происходят столкновения (частота столкновений) Z, определяемая

выражения-

ми (2.256), (2.257), равна приблизительно

36 1 3

10 c м

−

⋅

даже при комнатной

температуре. Если бы наличие столкновений было бы единственным фактором,

необходимым для протекания реакции, то все газовые реакции заканчивались

бы за

−

c, но это не так. Более того, частота столкновений зависит от квад-

ратного корня из температуры [см. уравнения (2.256), (2.257)], и поэтому, пред-

сказывая абсурдно неверную скорость, мы также предсказываем абсурдно не-

верную температурную зависимость.

Причина наблюдаемого столь резкого увеличения скорости реакции с по-

вышением температуры заключается в том, что для акта химического

взаимо-

действия само по себе столкновение частиц исходных веществ еще недостаточ-

но. Для того чтобы столкновение было эффективным, т. е., чтобы реагенты

могли прореагировать, они должны, как известно (см. 2.2.1.9), обладать запасом

Строго говоря,

представляет собой число столкновений с энергией, большей Е при ее

удовлетворении данному условию.

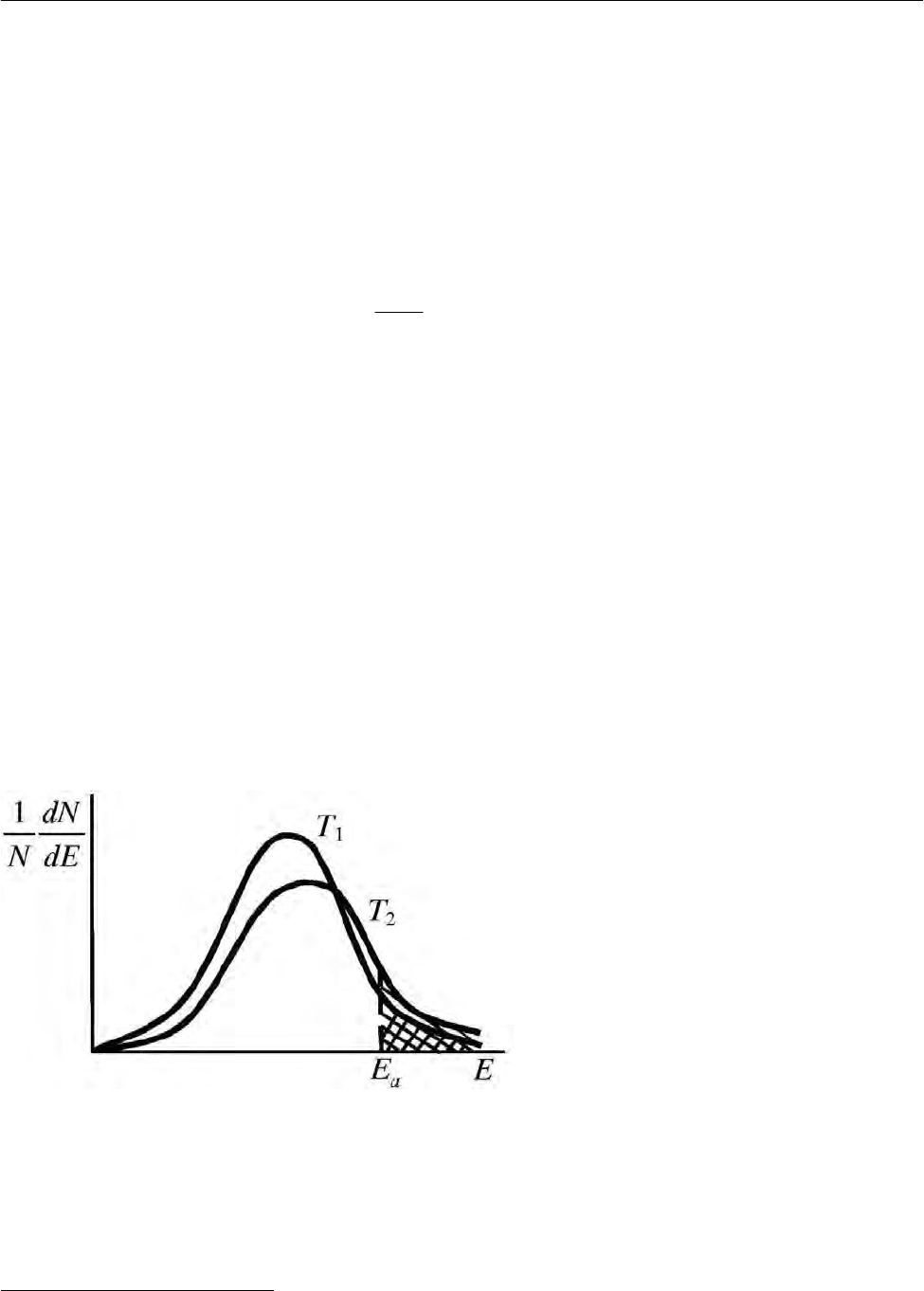
В. Е. Коган, Г. С. Зенин, Н. В. Пенкина

138

Рис.2.30. Распределение молекул по энер-

гиям

(

)

TT>

энергии, равным или большим энергии активации

. Число активных молекул

(частиц)

N , обладающих энергией

E≥ , составляет относительно малую

долю от общего числа молекул (частиц)

N. Доля молекул, энергия которых рав-

на или больше

, исходя из кинетической теории газов, равна множителю

/ERT

−

, аналогичному множителю в распределении Больцмана, т. е. определя-

ется распределением Больцмана

ERT

−

= . (2.267)

Кривые зависимости от

Е доли молекул, энергии которых лежат в пределах от

Е до Е + 1

, при двух температурах приведены на рис. 2.30. Кривые проходят

через максимум, смещающийся при повышении температуры в сторону бóль-

ших энергий. Это означает, что с повышением температуры увеличивается чис-

ло молекул, обладающих повышенными энергиями. Действительно, как на-

глядно видно из рис. 2.30, площадь, лежащая под кривой и ограниченная слева

ординатой

, равная доле молекул, энергия которых превышает значение

(заштрихованная область), увеличивается с ростом температуры. Увеличение

доли активных частиц приводит к росту числа активных (эффективных) столк-

новений

и соответственно к увеличению константы скорости и скорости

химической реакции.

Таким образом, если пред-

положить, что для осуществле-

ния реакции столкнувшиеся мо-

лекулы должны иметь, по край-

ней мере, энергию

, то частота

столкновений должна быть ум-

ножена на долю молекул, стал-

кивающихся, по крайней мере, с

энергией

. Из этого следует,

что температурная зависимость

скорости в рамках этой модели

определяется выражением

−

которое имеет форму аррениусовского выражения (2.215) и практически является

Принцип анализа этих кривых аналогичен анализу кривых, приведенных на рис. 2.28.

Х и м и ч е с к а я к и н е т и к а

139

уравнением (2.266) кинетической теории газов применительно к конкретному

значению энергии активации

. При низких температурах доля эффективных,

энергетически достаточных столкновений

очень мала и, таким образом,

данная модель предсказывает скорость, которая значительно меньше, чем вели-

чина Z. Более того, модель предсказывает экспоненциальную температурную

зависимость, поскольку доля энергетически достаточных столкновений экспо-

ненциально увеличивается с температурой. На данной стадии обсуждения име-

ется лишь одно затруднение, связанное с тем, что частота столкновений сама по

себе

зависит от температуры, в то время как в соответствии с экспериментом

предэкспоненциальный множитель А в аррениусовском выражении (2.215) от

температуры, вероятно, зависеть не должен. Однако фактически экспоненци-

альная зависимость от температуры значительно сильнее, чем зависимость Z от

квадратного корня из температуры [см. выражения (2.256), (2.257)], и экспери-

ментально обнаружить отклонения от экспоненциальной формы очень трудно

2.2.2.3. Теория активных столкновений

Исторически первым направлением в развитии взглядов Аррениуса была

теория активных столкновений (соударений), разработанная применительно к

бимолекулярным реакциям второго порядка на основании использования кине-

тической теории газов. Основные допущения и упрощения, принятые в этой

теории можно обобщить двумя положениями.

1. Акт превращения реагентов в продукты совершается в момент столк-

новения активных молекул

и протекает мгновенно.

2. Молекулы являются бесструктурными частицами

Помимо этого, в теории активных столкновений, безусловно, приняты и все

предположения кинетической теории газов.

1. Газ состоит из множества частиц (молекул) с массой

m, находящихся в

непрерывном беспорядочном движении, причем их траектории между двумя

столкновениями представляют прямые линии.

2. Частицы (молекулы) имеют малые размеры (диаметры) по сравнению

со средним расстоянием между ними.

В действительности химические реакции происходят путем постепенной перестройки мо-

лекул и перераспределения энергии между химическими связями.