Коган В.Е., Зенин В.С., Пенкина Н.В. Физическая химия. Часть 2. Химическая кинетика

Подождите немного. Документ загружается.

В. Е. Коган, Г. С. Зенин, Н. В. Пенкина

150

распределение электронной плотности между ядрами. При этом структура по-

тенциального поля в реагирующей системе будет функцией пространственных

координат, определяющих расположение ядер в молекулах.

Как было отмечено, мы будем вести рассмотрение в рамках адиабатиче-

ского приближения, что допустимо для

электронно-адиабатических процес-

сов

, т. е. процессов, которые происходят без изменения электронного состояния

системы. В рамках этого приближения каждому

i-му электронному состоянию

системы отвечает единственная функция потенциальной энергии, которая зави-

сит от координат ядер. Как известно [3], если система состоит из

n атомов, то

при неколлинеарной конфигурации эта функция зависит от 36

n − независимых

переменных. Это следует из того, что из числа координат атомов 3

n надо вы-

честь шесть степеней свободы, относящихся к движению системы как целого (3

поступательные и 3 вращательных степени свободы). Уравнение

(

)

пот 12 36

,,…,

Efxxx

−

, (2.286)

где

12 36

,,…,

−

– координаты, определяющие расположение ядер в простран-

стве, задающее поверхность в пространстве размерности 36

n − , называют

уравнением поверхности потенциальной энергии.

Топография

поверхности потенциальной энергии (ППЭ) зависит от

природы сталкивающихся частиц. На ней имеются максимумы, минимумы, пе-

ревалы, долины и т. д. ППЭ может зависеть от многих переменных, и это за-

трудняет представление ее в наглядном виде. Для упрощения рассмотрим

столкновение атома А с двухатомной молекулой ВС. При таком столкновении

могут происходить различные элементарные процессы. Ограничимся

рассмот-

рением прямой обменной реакции, уравнение которой

ABC ABC

→+. (2.287)

Потенциальная энергия этой системы зависит от трех координат: рас-

стояния между атомами В

и С

()

r , расстояния от атома А до центра масс мо-

лекулы ВС

(

)

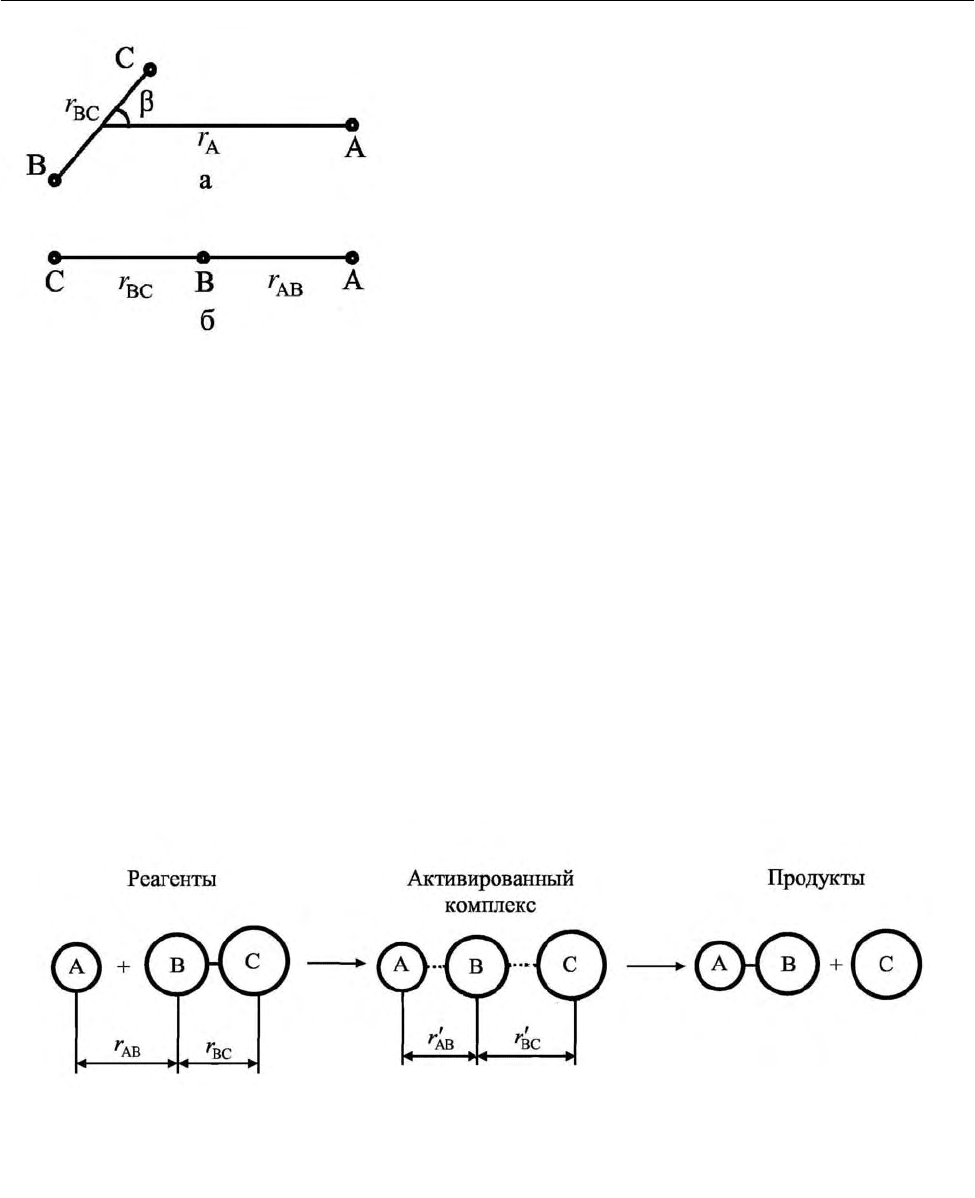
r и угла β (рис. 2.32, а).

Дальнейшее рассмотрение проводится для основного электронного состояния. Поэтому ин-

декс «

i» опускается или, в некоторых случаях, заменяется индексом «0».

Х и м и ч е с к а я к и н е т и к а

151

Для уменьшения числа координат за-

фиксируем значение ,

β=π, т. е. будем рас-

сматривать коллинеарное столкновение (рис.

2.32, б). В этом случае потенциальная энергия зависит только от двух коорди-

нат:

BC A

и rr. Вместо

r можно выбрать другую координату, например расстоя-

ние

r между атомами А и В.

Согласно теории активированного комплекса механизм реакции, уравне-

ние которой (2.287), схематически изображенный на рис. 2.33, заключается в

сближении атома А с молекулой ВС, в процессе которого ослабляется связь

– С и возникает связь А – В. Процесс завершается образованием молекулы

АВ

и атома С, для чего система должна пройти через активированный комплекс

()

ABC

≠

, когда атом В в одинаковой степени принадлежит молекулам ВС и АВ:

()

ABC ABC ABC

≠

+→ →+

. (2.288)

Изменения потенциальной энергии в ходе протекания реакции с учетом

принятых выше координат, функцией которых является потенциальная энергия,

могут быть представлены трехмерной диаграммой, на двух осях которой нано-

сят соответственно координаты

, а на третьей – отвечающую им энер-

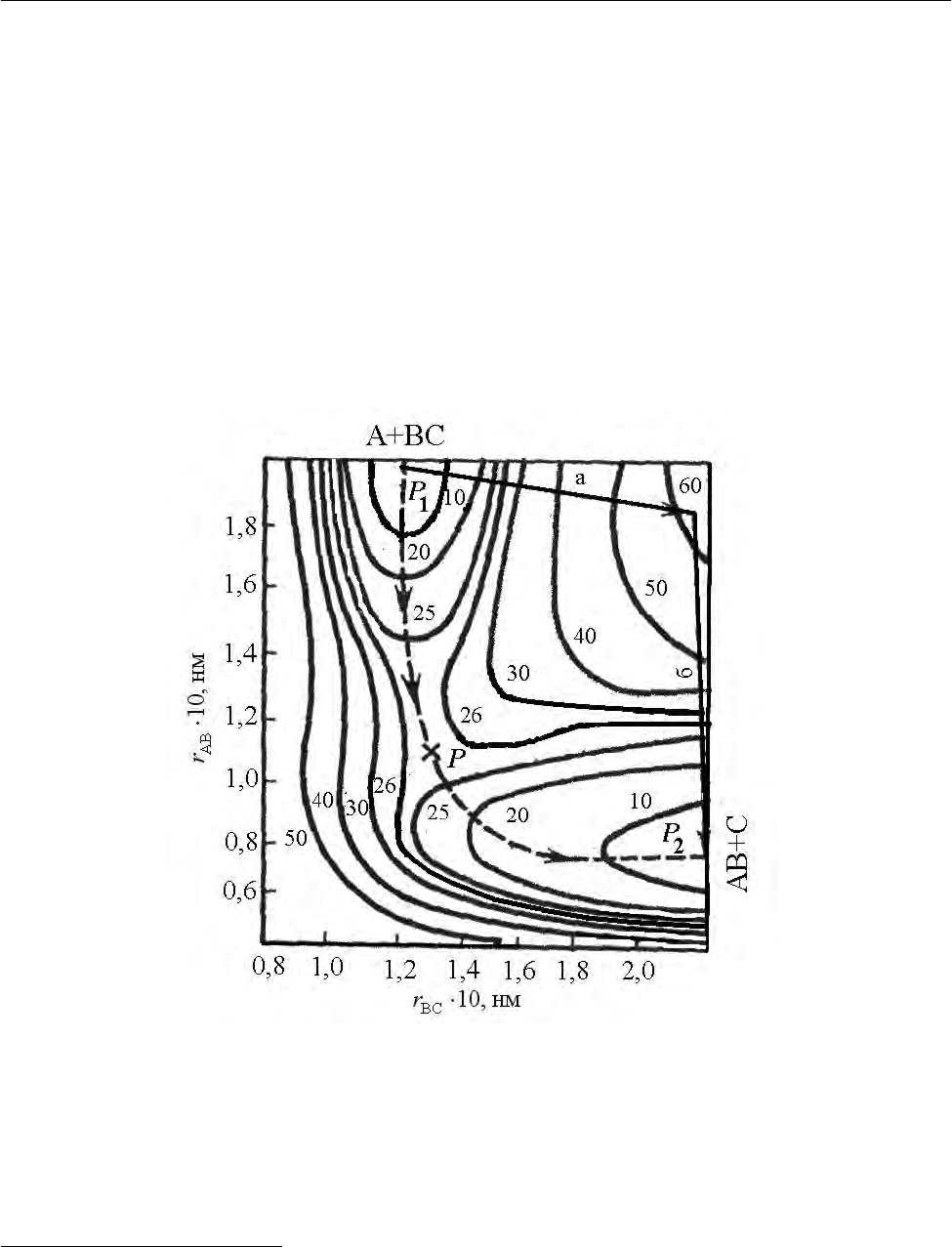
Рис. 2.33. Схематическое изображение механизма реакции, уравне-

ние которой (2.287):

AB AB BC BC

,rrrr

′

Рис. 2.32. Относительное расположение трех

взаимодействующих атомов при неколлинеар-

ной (а) и коллинеарной (б) конфигурации

В. Е. Коган, Г. С. Зенин, Н. В. Пенкина

152

гию

. Трехмерную диаграмму можно заменить двухмерной, если на горизон-

тальную плоскость, ограниченную координатами

r и

r , нанести линии рав-

ной энергии –

изоэнергетические линии, представляющие собой проекции се-

чения энергетической поверхности плоскостями, перпендикулярными к оси

энергии. Данный метод изображения трехмерной поверхности на плоскости яв-

ляется принятым в орографии

методом горизонталей, в соответствии с кото-

рым поверхность рассекают равноудаленными горизонтальными плоскостями и

проецируют контуры сечения на плоскость. Поэтому изоэнергетические линии

часто называют также

горизонталями.

Пример получаемой таким образом «карты» ППЭ представлен на рис. 2.34.

Для более сложных случаев требуется многомерная диаграмма.

Орография (от греч. orόs – гора и … графия) раздел геоморфологии, занимающийся описа-

нием и классификацией форм рельефа по их внешним признакам вне зависимости от проис-

хождения.

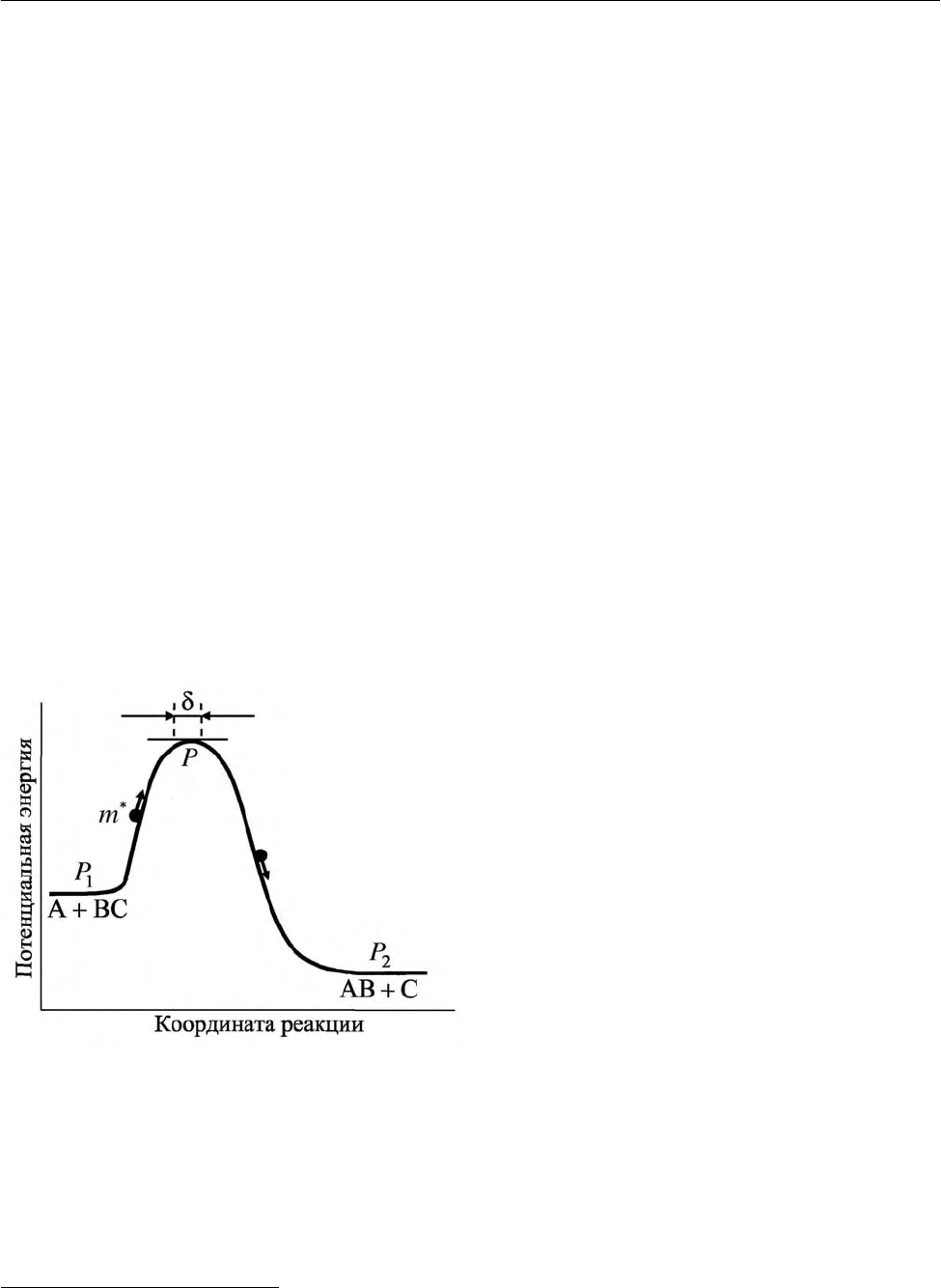
Рис. 2.34. Карта поверхности потенциальной энергии при реакции,

уравнение которой (2.287):

кривые – горизонтали (изоэнергетические линии); цифры у горизон-

талей – энергия в условных единицах; пунктирная линия – путь (ко-

ордината) реакции

Х и м и ч е с к а я к и н е т и к а

153

Очевидно, что густота расположения горизонталей свидетельствует о крутизне

склона поверхности. На энергетической карте можно выделить «долину»

P , в

которой система ABC

находилась до реакции, и «долину»

P , в которой на-

ходится система AB C

, возникшая в результате реакции. Переход системы от

P к

P связан с преодолением энергетического барьера, разделяющего эти до-

лины. Энергетически наиболее выгодным для такого перехода является путь,

проходящий по «ложбине» через самую низкую точку «перевала»

Р. Точка Р и

соседние с ней участки отвечают области существования активированного ком-

плекса, отличающегося от стабильных молекул своей неустойчивостью вдоль

пути реакции. По отношению к изменениям в других направлениях активиро-

ванный комплекс устойчив, так как эти изменения энергетически невыгодны.

Энергетически невыгодны и любые другие пути протекания реакции, уравне-

ние которой (2.287). Например, можно представить

себе первоначальную дис-

социацию молекулы ВС

на свободные атомы с последующей рекомбинацией А

и В. Это означало бы первоначальный подъем реагирующей системы на плос-

кое плато с последующим спуском в долину продуктов

P . Такой путь пред-

ставлен на рис. 2.34 стрелками

а и б. Понятно, что так как плато находится зна-

чительно выше перевала

Р, то необходимая затрата энергии

∆ была бы при

этом значительно выше. Вероятность того или иного процесса (и скорость его

осуществления) пропорциональна множителю

/ERT

−

∆

, быстро убывающему с

увеличением

∆ . Поэтому в подавляющем большинстве случаев реакция осу-

ществляется по пути наименьшей затраты энергии.

Исходя из обычных термодинамических свойств [3] активированный

комплекс, содержащий

n атомных ядер должен иметь 3n степеней свободы, из

которых 3 степени свободы приходится на поступательное движение системы в

целом, 3 (или 2 для линейного строения переходного состояния) – на враща-

тельное движение и

(

)

36или 35nn−− – на колебательное движение. Однако

активированный комплекс отличается от обыкновенных молекул тем, что вдоль

пути реакции он находится на вершине потенциального барьера и вместо одной

колебательной степени свободы имеет дополнительную внутреннюю поступа-

тельную степень свободы вдоль пути реакции

. Таким образом, в активирован-

Термины «путь реакции», «поступательное движение» и другие относятся к движению фи-

гуративной точки активированного комплекса по ППЭ, но не к перемещению его самого в

пространстве.

В. Е. Коган, Г. С. Зенин, Н. В. Пенкина

154

ном комплексе, содержащем n атомных ядер, внутренняя энергия переходного

состояния будет определяться одной степенью свободы поступательного дви-

жения вдоль координаты реакции и 37(или 36

−

− для линейного активиро-

ванного комплекса) степенями свободы колебательного движения. Данная осо-

бенность активированного комплекса обусловлена тем, что, совершив половину

колебания, он скатывается на энергетической диаграмме с перевала

Р в долину

P , распадаясь на продукты. Сформулированное выше относится уже к реаги-

рующему активированному комплексу и может не учитываться при его рас-

смотрении в качестве обычной молекулы. В этом случае рассматриваются

только 3

n – 1 степеней свободы, из которых 3 степени свободы приходится на

поступательное движение системы в целом, 3 (или 2 для линейного строения

переходного состояния) – на вращательное движение и

(

)

37или 36nn

−

− – на

колебательное движение

Если сделать разрез ППЭ, перпендикулярный к плоскости чертежа и про-

ходящий вдоль пути реакции, а затем развернуть поверхность разреза в одну

плоскость, то получим кривую, которую можно назвать энергетическим профи-

лем пути реакции (рис. 2.35).

При условии, что энергия по-

ступательного движения молекулы

АВ и атома С

будет достаточна вели-

ка, система сможет достигнуть пере-

вала и спуститься к конечному со-

стоянию. Если же кинетическая энер-

гия поступательного движения моле-

кулы АВ и атома С

будет мала, то

система при столкновении не достига-

ет величины энергетического барьера

и скатится к начальному состоянию.

Высота максимума (рис. 2.35), или

разность между энергией основного

состояния активированного комплек-

са

≠

и реагентов

() ()

(

)

0AB 0C

EE+ дает истинную энергию активации реакции

Здесь и далее наличие верхнего правого индекса

≠

указывает на отнесение рассматривае-

мой величины к активированному комплексу.

Рис. 2.35. Энергетический профиль

пути реакции, уравнение которой

(2.287)

Х и м и ч е с к а я к и н е т и к а

155

() ()

(

)

0AB 0C

EE E E

≠

=− +

. (2.289)

Рассмотренный материал и сведения, приведенные в 2.2.1.9, позволяют

заключить, что построение ППЭ решает ряд важных задач и, в первую очередь,

показывает принципиальный путь теоретического расчета энергии активации,

который пока недоступен в связи с математическими сложностями. Во-вторых,

положение «перевальной точки» на ППЭ непосредственно дает межатомные

расстояния в переходном состоянии. Кроме того,

при условии точного построе-

ния ППЭ конфигурация «перевальной седловины» могла бы дать информацию

о колебательных характеристиках переходного состояния.

Все эти данные необходимы для полного теоретического расчета скоро-

сти реакции. Построение ППЭ является первым этапом такого расчета.

С учетом отмеченных математических трудностей в настоящее время

пользуются приближенной математической моделью, так называемой

теорией

абсолютных скоростей реакций

, предложенной в 1935 году Г. Эйрингом и

М. Поляни. Эта математическая модель, используя некоторые упрощающие

предположения о свойствах активированного комплекса, впервые позволила

приближенно оценить предэкспоненциальный множитель. Энергию активации

в этой теории не рассчитывают, а рассматривают как опытную величину.

В. Статистический аспект

Для проведения статистического расчета скорости реакции в рамках рас-

сматриваемой теории прибегнем к механической аналогии. Взаимные превра-

щения кинетической и потенциальной энергий в трехатомной системе, отве-

чающей уравнению (2.287), будем изображать как аналогичные превращениям

энергий тяжелой материальной частицы с некоторой

эффективной массой m

∗

скользящей без трения в гравитационном поле по ППЭ. Такой подход полно-

стью оправдывает себя при надлежащем подборе эффективной массы. Следует

подчеркнуть, что эффективная масса не является массой самого активирован-

ного комплекса. Это вспомогательная величина, не присутствующая в оконча-

тельных результатах и зависящая, например, от напряженности силы тяжести.

Вернемся к рассмотрению

энергетического профиля пути реакции, урав-

нение которой (2.287), приведенного на рис. 2.35, на котором такая частица

(будем далее называть ее частицей

∗

) изображена кружком. Если частица

∗

обладает достаточной кинетической энергией, то сможет взобраться на пере-

В. Е. Коган, Г. С. Зенин, Н. В. Пенкина

156

вальную точку Р и далее скатится со все возрастающей скоростью в сторону

продуктов реакции. Другими словами, в этом случае в рассматриваемой трех-

атомной системе относительная кинетическая энергия при сближении частиц А

ВС достаточно велика для преодоления силы отталкивания и образования пе-

реходного состояния, которое затем распадается на продукты.

В рамках проводимой аналогии понятно, что скорость протекания эле-

ментарного акта определяется скоростью пересечения вершины перевала час-

тицей

∗

. Скорости пересечения, являющиеся по существу проявлением тепло-

вого движения молекул, будут самыми различными в разных актах, но при дан-

ной температуре скорость можно охарактеризовать какой-то средней величи-

ной. Для упрощения расчета делается предположение о существовании на вер-

шине перевала плоского участка пути реакции длиной

(рис. 2.35), что равно-

сильно допущению о существовании переходного состояния не в одной точке

при строго фиксированных координатах – расстояниях

, но в некото-

ром интервале этих расстояний. Однако это не является принципиальным, так

как величина δ произвольна, вводится лишь для наглядности расчета и выпада-

ет из конечного результата. Принятие вершины перевала плоской позволяет

движение фигуративной (изображающей) частицы на этом участке пути счи-

тать

одномерным. Тогда среднюю скорость пересечения перевала можно рас-

считать по формуле(2.242), как среднюю скорость теплового движения молеку-

лы с массой

∗

вдоль одной координаты

1/2

∗

⎛⎞

⎜⎟

⎝⎠



Имеющиеся данные позволяют легко определить среднюю продолжительность

жизни переходного состояния:

1/2

∗

⎛⎞

τ= =δ

⎜⎟

⎝⎠



. (2.290)

Вполне естественно считать распад переходного состояния, т. е. реакцию

ABCABC→+

…… ,

мономолекулярной реакцией первого порядка. Как было показано при рассмот-

рении консекутивных реакций (см. 2.2.1.5), средняя продолжительность жизни

Х и м и ч е с к а я к и н е т и к а

157

вещества при его распаде является величиной обратной константе скорости ре-

акции. Тогда последняя определяется соотношением

()

1/2

∗

≠

⎛⎞

⎜⎟

⎝⎠

, (2.291)

а скорость реакции равна

()

1/2

kc c

∗

≠

≠≠

⎛⎞

⎜⎟

⎝⎠

v . (2.292)

Входящая в выражение (2.292) концентрация активированных комплексов не

известна и должна быть заменена более легко определимыми величинами. Для

этого используется допущение, введенное еще Аррениусом. Это допущение о

равновесии между активными состояниями и реагентами

ABC A B C+

……, (2.293)

позволяющее переписать уравнение (2.288), отражающее механизм реакции,

уравнение которой (2.287), следующим образом:

ABC A B C ABC+→+

…… . (2.294)

Допущение о равновесии между активными состояниями и реагентами позво-

ляет написать константу равновесия для первой стадии реакции, уравнение ко-

торой (2.294), в виде

ABC

≠

= . (2.295)

Решая уравнение (2.295) относительно концентрации

≠

и подставляя ее в вы-

ражение (2.292), получаем

ABC

1/2

∗

≠

⎛⎞

⎜⎟

⎝⎠

v . (2.296)

Для перехода от скорости реакции к константе скорости воспользуемся выра-

жением основного закона для бимолекулярной реакции второго порядка (2.15):

()

ABC

kcc

. (2.297)

Сопоставляя выражения (2.296) и (2.297), находим константу скорости

рассматриваемой реакции:

В. Е. Коган, Г. С. Зенин, Н. В. Пенкина

158

()

1/2

∗

≠

⎛⎞

⎜⎟

⎝⎠

. (2.298)

Выражение (2.298) остается справедливым и для любой другой реакции. Все

различия будут заключаться в способе написания константы равновесия акти-

вированного комплекса.

Для определения

≠

воспользуемся методами статистической термоди-

намики, позволяющими выразить константу равновесия через суммы по со-

стояниям на единицу объема

qQV

. (2.299)

Запись константы равновесия через суммы по состояниям аналогична хорошо

известной из термодинамики [3] записи ее через концентрации

, но с добав-

лением множителя

/URT

−

∆

, содержащего тепловой эффект реакции при абсо-

лютном нуле

UE∆=∆

. Применительно к рассматриваемому случаю констан-

та будет иметь вид

(

)

ABC

/ERT

≠

−

≠

. (2.300)

В выражении (2.300) теплота реакции при абсолютном нуле, которая

должна была бы стоять в показатели степени, заменяется энергией, затрачивае-

мой на образование активированного комплекса, –

энергией активации при

абсолютном нуле

≠

. В развернутом виде она записывается так:

() ( )

EUU U

≠

=− − ,

где

()

0 i

– энергии реагентов процесса активации при абсолютном нуле.

Для реагентов обычно не составляет труда нахождение на основании мо-

лекулярных характеристик сумм по состояниям

ABC

и qq

. Поэтому, опуская вы-

воды, приведем лишь основные соотношения, используемые при этом.

Полную молекулярную сумму по состояниям можно представить как

произведение сумм, вычисленных для отдельных видов энергии, т. е.

пост эл кол вр

QQ QQQ

. (2.301)

Поступательная сумма по состояниям для частицы массой m равна

Х и м и ч е с к а я к и н е т и к а

159

()

3/2

пост

2 mT

, (2.302)

где

V – объем.

Электронная сумма по состояниям при не очень высоких температурах

равна вырожденности (мультиплетности) основного электронного уровня, т. е.

0эл

. (2.303)

Этот множитель обычно включают в поступательную сумму по состояниям.

Колебательная сумма по состояниям в общем случае, когда число ви-

дов колебаний составляет 3

nx− , записывается следующим образом:

()

кол

hv T

−

≈−

∏

, (2.304)

где

v – частота колебаний,

−

;

– характеристическая температура [3].

Вращательная сумма по состояниям определяется в зависимости от

типа молекул следующим образом:

- для несимметричных двухатомных молекул

вр

8 T

, (2.305)

где

r=µ – момент инерции,

– приведенная масса, r – межъядерное рас-

стояние;

- для симметричных двухатомных молекул

вр

; (2.306)

- для линейных многоатомных молекул с осевой симметрией

вр

18 T

, (2.307)

где

σ – число симметрии, равное числу неразличимых состояний, получаю-

щихся при вращении молекулы на 360

;

- для тетраэдрических молекул